案例教学在大学专科数学建模教学中的应用

郭 辉，屈 哲，郑 虹

(青岛滨海学院，山东 青岛 266555)



案例教学在大学专科数学建模教学中的应用

郭 辉，屈 哲，郑 虹

(青岛滨海学院，山东 青岛 266555)

围绕实现大学专科层次学生的培养目标，以运筹学中的加工方式选择问题为教学案例，通过将案例教学法具体运用到该问题的准备、分析、讨论、归纳总结等各教学阶段，论证了案例教学在大学专科数学建模教学中的必要性、可行性、有效性问题。

案例教学；数学建模；专科；线性规划

一、案例与案例教学

案例就是为实现一定的教学目的，以事实为素材编写的对某一实际情境的客观描述。案例通常具有真实性、完整性、典型性和启发性等特点。教学中所选择的案例应该能够引人深思，启迪思路，帮助学生深化理解教学内容[1]。

案例教学，即教育者以案例为基本教学材料，通过师生之间、学生之间的多向互动、平等对话和积极研讨等形式，通过分析解决案例所设定的问题，做出决策的一种教学方法。案例教学不仅强调教师的“教”(引导)，更强调学生的“学”(研讨)，主要特点包括：(1)明确的目的性，即在案例教学中，案例的编写和教学设计，都为了实现特定的教学目标；(2)结果多元性，即案例教学不刻意寻找惟一答案，但可从多种解答中选出最佳答案；(3)学生的主体地位，在案例教学中，学生是案例教学的主体，教师的职责是精心编写案例，指导课堂讨论，学生在教师的指导下，积极参与到案例所描述的情境中，充分体验案例角色，对案例进行分析、讨论，在此过程中相互学习提高；(4)较强的综合性，案例的分析需要学生具备相应的理论知识，还应审时度势、权衡应变、果断决策，需要学生综合运用各种知识和交流技巧来处理案例中涉及的问题，提高分析和解决实际问题的能力[2]。

二、大学专科数学建模课程的教学规划

(一)大学专科教育培养目标

大学专科教育是我国高等教育的重要组成部分，其培养目标和对象不同于普通本科教育，目标是培养学生的实践能力和创新精神，对象是面向生产和服务一线岗位所需要的技术技能型人才。这类人才主要从事技术性管理或高智能技术操作或技术服务，其知识能力结构特点是:专业技术知识面宽、实践能力强。

(二)数学建模在大学专科教育体系中的作用

数学作为大学专科重要的基础课程，不仅能够培养和提高学生的逻辑思维能力和创新思维能力，而且在培养学生科学理性精神方面也发挥重要作用，同时还是学生学习专业课程的基础，在人才培养过程中起基础性作用。但目前大学专科数学教学存在着理念落后、学生学习的积极性不足、数学应用能力较低等问题，这些问题制约着大学专科学生培养目标的实现，根据《中共中央国务院关于深化教育改革全面推进素质教育的决定》，大学专科数学教学改革应该体现创新能力培养的总目标，体现学生逻辑思维、创新能力的培养，教学应由“教师为中心”向“教师为主导，学生为主体”转变。而作为联系数学理论和实际问题桥梁作用的数学建模教学正好适应了这一要求，体现了大学专科数学教学应该注重应用性的特点，所以大学专科学生学习数学建模就成为数学教学改革的重要抓手。

(三)大学专科数学建模教学应坚持案例教学

数学建模采取案例教学就是在教师的引导下，学生通过对实际案例的分析与讨论，系统地运用数学方法综合分析和解决实际问题，把学生从课堂的被动位置推到主动位置上，学生通过对实际问题分析、讨论和比较，寻求解决问题的最佳方案，这种教学方法有利于调动学生的主动性和积极性，较好地解决理论联系实际问题。数学建模教学强调对实际问题的分析和讨论，要求学生从不同立场、不同角度分析问题，注重问题的解决过程和解决方法，特别强调学生团队合作意识和创新能力[3]。这一过程体现了应用型人才的培养要求，与大学专科教育培养目标一致，因此，在大学专科数学建模教学应坚持案例教学法。

三、数学建模课程案例教学实施方案

数学建模课程案例教学实施方案大致可分为准备阶段、分析阶段、讨论阶段和总结阶段[4]，案例教学实施流程如图1所示。本部分通过以运筹学中线性规划模型中的加工方式选择问题为例，论证数学建模采取案例教学的实施方案。

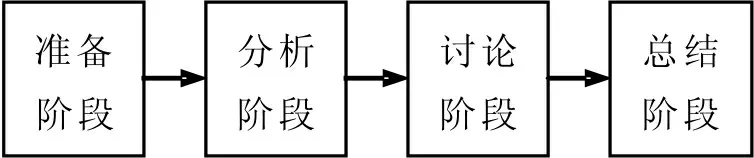
图1 案例教学实施流程

(一)准备阶段

准备阶段是顺利实施数学建模案例教学的重要保证，为了培养学生掌握线性规划的理论和方法，教师根据培养目标和教学课程标准编写如下实际案例：某企业计划生产4000件A产品，该产品可以自己加工，也可以外协加工，生产的固定成本、单件成本每种生产形式的最大加工数量等具体要求如表1所示，针对这一生产过程，该企业怎样安排产品加工，才会使生产总成本最小。这一教学案例实际上就是为培养学生掌握“加工方式选择问题”而设计的[5]。为实现教学目的，教师应首先进行教学设计，明确案例教学目标、教学过程和教学手段，然后确定案例教学的重点和难点，最后拟定具体的案例教学计划，明确学生需要在课前查阅的运筹学相关知识，理解线性规划模型解决问题的范围和方案，掌握加工方式选择这类问题特点及其所需的建模方法，要求学生在课前准备期间掌握Lingo，Matlab等相关数学软件在运筹学中的运用等，再根据学生的课前准备情况进行合理分组。

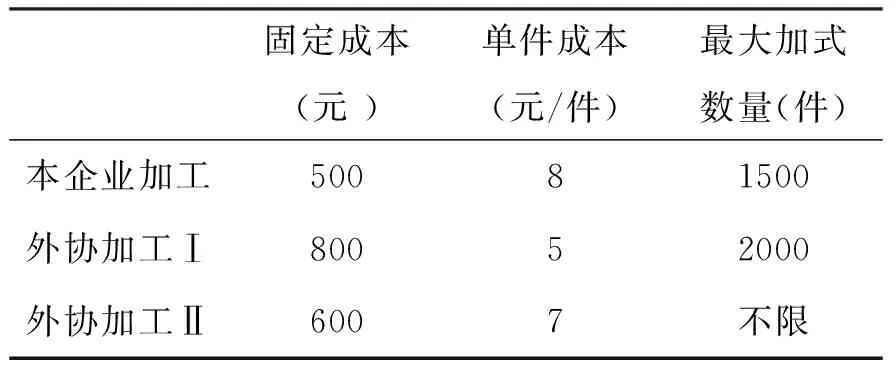
表1 企业产品加工具体要求

(二)案例分析阶段

作为案例教学的组织者，教师在该阶段需全面分析案例教学本身的内容结构，把握案例中的重点、难点和关键点，以便处理课堂讨论的时间分配、提示程度等问题；确定案例涉及的基本原理，引导学生在思考和讨论案例时学习运用相应的理论与方法。案例教学还需教师剖析案例所蕴含的深层次的教育价值，明确各个案例之间的教学联系，将《数学建模》整门课的教学作为一个整体通盘考虑，从而使案例教学克服就事论事、各个案例的教学支离破碎的弊端。

具体到每一次案例教学，教师需要从学生的课前准备情况和案例内容两个方面进行深入分析，根据培养目标对所编写的教学案例写出细致而全面的案例分析提纲，这样教师可以有效地调控整个教学过程，为教学过程中对学生进行及时引导与评价提供依据。在案例分析过程中教师应掌握各分组不同学生的知识储备情况，根据对学生的分析进一步优化学生分组，使各分组都组成最佳组合，分组确定后，各小组需对案例的解决方案进行深入分析，教师可根据学生的分析情况进行适当的引导，将可能出现的根本性错误及时予以纠正，将学生没有掌握的必要性知识点进行启发性讲解，比如针对加工方式选择问题，各小组在分析固定成本与生产方式的关系问题时，对于变量表示等技巧性问题，若学生运用不恰当，教师需采取启发教学法给予必要的提示，例如根据案例所设定的条件，某一种生产方式可以被采用，也可以不被采用，若该种生产方式被采用，其固定成本才产生费用，否则就不产生费用，固定成本与生产方式的这种关系应该采用0-1变量来表示[6]，否则最优的数学模型将难以建立，具体可设第j(j=1,2,3) 种生产方式的产品数量为xj件，令：

中j=1,2,3

由此可得第j种生产方式的费用可表示为：

cj=ajy1+cjxj

式中aj是固定成本，cj单位产品成本。

(三)案例讨论阶段

在数学建模案例教学中，教师和学生在对案例进行分析之后，就进入了组织讨论阶段，案例讨论是案例教学的主体和中心环节。案例讨论就是以学生为主体，充分发挥学生的主体性、积极性和创造性，让学生自主地、独立地深入思考，运用所学的知识分析与处理案例所涉及的问题，在数学建模案例教学中，可先进行小组讨论后进行班级讨论。小组讨论在个人分析的基础上，小组成员集体对案例进行细致、深入、全面地讨论，对解决问题的多种选择方案的取舍、利弊及其后果进行重点讨论，小组成员之间相互交流，每位学生都积极发言、参与讨论，然后各小组写出全面详细的分析报告，进行全班讨论。班级讨论需要由每个小组选派一名代表做中心发言，向全班同学陈述本小组的案例分析报告，主要包括对案例的理解、分析、判断、论证和决策过程，解决问题的实施方案和步骤说明，并对实施效果进行分析，小组其他同学进行补充，各小组都汇报完各自的工作后，教师组织全体学生对各小组的工作进行分析、讨论、评价，最佳结果往往是在激烈地争论和反复交流中逐步得到。

对于加工方式选择这一教学案例，在确定生产方式的费用核算这一关键点后，就需要通过讨论进一步明确实现总成本最低的约束条件，产品总数量约束为：x1≤1500,x2≤2000，yj和xj的关系线性化为：xj≤Myj，j=1,2,3，其中M是一很大的常数，此处可取为4000。当xj>0时，yj=1，xj=0时，为使总成本f最小，则yj=0；变量约束为：xj≥0，且为整数，j=1，2，3。

确定约束条件后，总成本的目标函数应设为：

f=(500y1+8x1)+(800y2+5x2)+(600y3+7x3)

至此初步建立起了该案例的数学模型，由于决策变量既有0-1变量又有整数变量，所以可用混合线性规划最终建立该案例的数学模型[7]，根据最终的讨论结果，建立混合线性规划模型为：

f=(500y1+8x1)+(800y2+5x2)+(600y3+7x3)

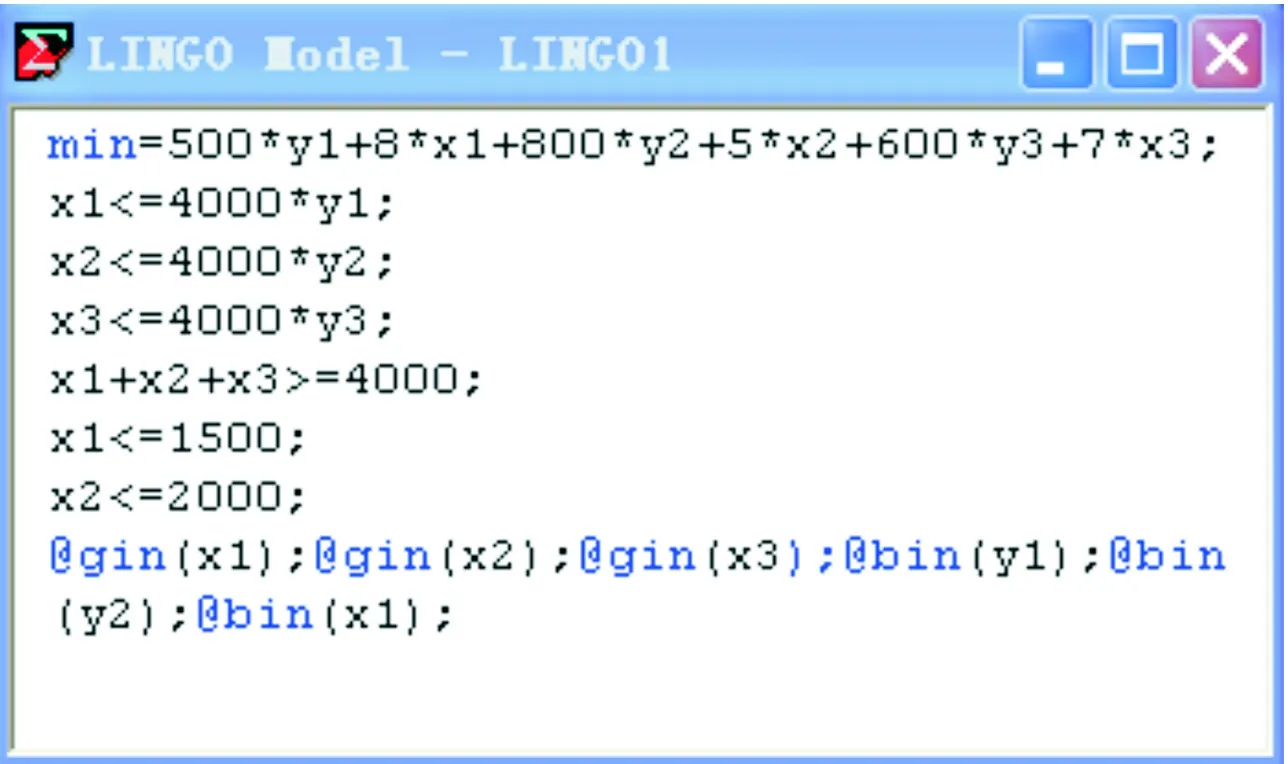
图2 案例教学实施流程

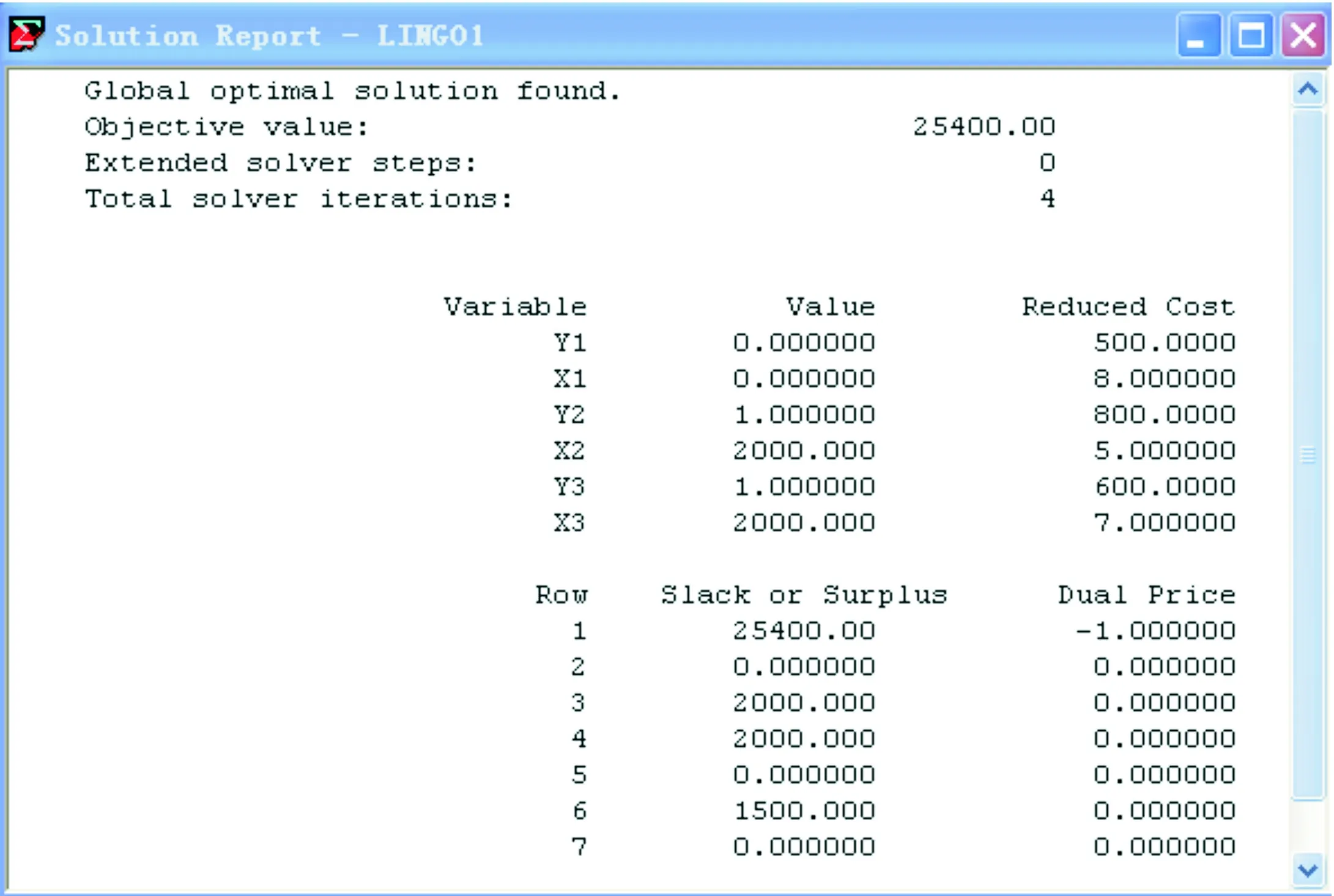
图3 Lingo求解结果

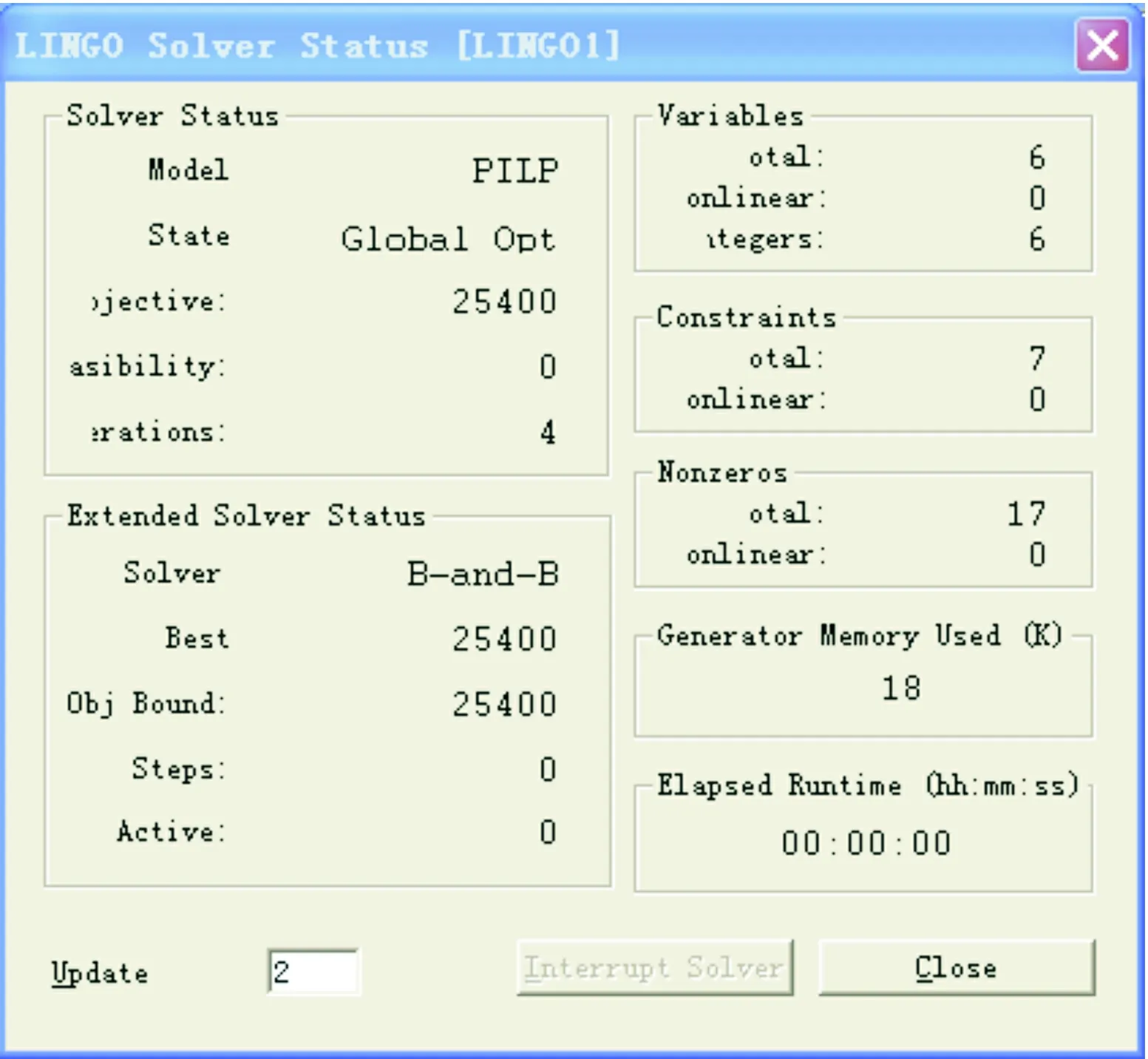
图4 求解结果的总结分析

数学模型成功建立后，需要运用数学软件进行求解，各小组所采用的数学软件可能不同，通过对各种数学软件的优缺点进行比较，由于Lingo软件作为求解线性规划问题的专业软件，比Matlab简洁实用[8]，易于学生理解掌握，所以可以选用Lingo软件对该案例模型进行求解，根据所建立的数学模型编写的Lingo计算程序如图2所示，求解结果如图3所示，对求解结果的总结分析如图4所示。

根据对Lingo软件的运行结果分析可得，为使总成本最小，企业对该批产品的最优加工方案：采用外协加工Ⅰ加工2000件，采用外协加工Ⅱ加工2000件，不采用本企业的加工方式，总成本最低为25400元。

案例讨论是案例教学的主要形式，在这一过程中，教师不再是传统的课程内容的讲授者，而要成为案例讨论的组织者和引导者，学生也不再是传统意义上的学习者，而是积极的参与者和分享者，不断在交流中吸取他人的成功理念，提高自己分析问题解决问题的能力[9]。案例讨论的有效进行，依赖于教师和学生角色的成功转化和有效引导和参与。

(四)案例教学归纳总结

在教师的积极引导下，经过全班同学的激烈讨论，得到案例的最优解决方案，教师需根据该最优解决方案，结合学生对案例分析和交流的情况做出归纳和总结，总结教学中选择的案例是否符合大学专科教育培养目标，是否符合教学设计要求，是否可以提高学生分析问题解决问题的能力，案例教学在课前准备、分析、讨论、归纳总结等各阶段的组织是否恰当，教学的重点和难点是否突出，对教学实施的安排是否与教学设计相符，案例教学是否达到了预期目的等等，通过归纳和总结本次案例教学的经验教训为下一次案例教学积累成功经验。

结语

为提高大学专科层次学生的数学应用能力，实现其培养目标，通过在运筹学的“加工方式选择问题”中运用案例教学法，论证了案例教学在大学专科数学建模教学中是非常必要、可行和有效的，研究表明数学建模采取案例教学符合应用型人才的培养要求，能够显著提高学生分析和解决实际问题的能力，强化学生的实践能力，培养学生的团队意识和创新精神，可以作为实现大学专科学生培养目标的一种教学手段。

[1] 吴云鹏. 教育学案例教学教程[M].上海：华东师范大学出版社, 2015.

[2] 皮修平，周镕基. 经济学综合案例教学[M].北京：中国人民大学出版社,2010.

[3] 高振滨，沈继红. 案例教学法在数学建模中的应用[J]. 教育探索,2011,(5):65-66.

[4] 张 兵. 案例教学在运筹学教学中的运用[J].徐州教育学院学报,2008,(3):153-154.

[5] 郭培俊, 毛海舟. 高职数学建模[M].杭州：浙江大学出版社,2010.

[6] 姜启源，谢金星，叶俊.数学模型[M].北京：高等教育出版社,2003.

[7] 袁新生，邵大宏，郁时炼. lingo和excel在数学建模中的应用[M].北京：科学出版社,2007.

[8] 郭景石. 高职数学教育改革中的数学建模[J].教育与职业,2011,(26):97-98.

[9] 陈照辉. 以数学建模分析为基础的运筹学案例教学[J].重庆科技学院学报：社会科学版,2011,(23):170-171.

(责任编辑：高 曼)

10.3969/j.issn.1009-2080.2016.06.023

2016-11-09

青岛滨海学院教学改革研究项目(2014J10)。

郭辉(1971-)，男，山东青岛人，青岛滨海学院讲师，硕士。

G642.4

B

1009-2080(2016)06-0101-04