套筒节点受压力学性能
李思遥, 李雄彦, 薛素铎, 叶继红
(1.城市与工程安全减灾教育部重点实验室(北京工业大学),北京100124;2.混凝土及预应力结构教育部重点实验室(东南大学),南京210018 )
套筒节点受压力学性能
李思遥1, 李雄彦1, 薛素铎1, 叶继红2
(1.城市与工程安全减灾教育部重点实验室(北京工业大学),北京100124;2.混凝土及预应力结构教育部重点实验室(东南大学),南京210018 )
套筒节点是一种新型的装配式空间网格结构节点,其螺纹外伸端为关键受力区域.为了解该节点受压力学性能,首先利用ANSYS对节点进行数值分析模型比选,提出可行的分析模型,研究节点受压性能和应力分布规律;通过试验考察轴心受压、偏心受压作用下节点外伸端受力特征和破坏机理;然后对试件数值模拟结果与试验数据进行对比,验证数值模拟方法的准确性;最后基于数值模拟和试验结果,推导出节点抗压承载力和刚度计算公式.研究表明:套筒节点轴压时承载力约为相同材料等直径、等壁厚圆管的63.2%;当存在较大偏心时,节点偏压承载力约为轴压时的83.9%;轴压试件与偏压试件破坏形式一致,均为螺纹外露段屈曲破坏;数值模拟得到的节点抗压性能与试验结果吻合较好,节点分析模型合理;理论分析得到的节点承载力和刚度计算公式与试验结果吻合较好.套筒节点受力合理可靠,其薄弱部位为螺纹外露段,受压时呈屈曲破坏.关键词: 套筒节点;受压力学性能;有限元分析;试验研究
建筑装配化可减少劳动力成本、提高生产效率,已成为建筑行业的发展趋势.空间网格结构因其优良的力学性能,已成为广泛应用的一种空间结构形式[1].焊接球和螺栓球为网格结构常用节点.焊接球节点因其需要现场焊接,无法满足装配化需求[2];螺栓球节点可实现装配化施工,但常出现“假拧紧”和“合拢塞杆困难”等问题[3-4].网格结构的装配化水平与节点构造有密切联系,针对节点构造,国内外学者进行了相关研究.文献[5-6]对装配式四角锥网架结构体系进行理论及试验研究,但针对节点性能未进行专门研究;文献[7]提出了装配式木结构网壳,并对节点强度进行试验研究;文献[8]对一种新型铸铝网格结构节点进行试验和刚度研究,但尚未应用于实际工程;文献[9-12]对装配式碗式节点网壳、装配式螺栓球壳展开了系统研究,并成功应用于工程实践.目前,国内外学者对于装配式空间网格结构的研究尚处于起步阶段,工程应用处于探索阶段,尚未形成标准化的建筑结构产品.
针对中小跨度空间网格结构的装配化问题,作者所在团队提出一种新型套筒节点[13-14],该节点通过其螺纹外伸端实现杆件的快速连接.作者对套筒节点外伸端螺纹构造参数进行了数值分析,并提出参数选取原则[13];通过拉伸试验,研究其受拉力学性能[14].前期研究发现,该节点拉、压力学性能存在一定差异.为系统考察套筒节点的受压力学性能,根据文献[13]研究结论,本文对节点进行了受压力学性能数值分析和试验研究,推导了节点受压承载力计算公式.
1 节点受压力学性能数值模拟
1.1 有限元模型建立
套筒节点的构造见图1.数值模拟时套筒节点材料为Q345钢,弹性模量E=2.06×105MPa,泊松比μ=0.3,屈服强度为345 MPa.钢材采用各向同性双线性本构模型[15],强化模量为0.02.节点螺纹牙型为普通三角形,螺纹接触分析时钢材-钢材静摩擦系数为0.12.根据套筒节点几何特点,仅选取其1/2建立ANSYS分析模型,采用SOLID185单元,接触对选择TARGE170、CONTA174单元.采用ANSYS分析时,若采用螺旋曲面建立螺纹,存在大量曲面接触问题,计算不易收敛[16].基于文献[17]研究成果,可将螺纹简化为水平锯齿状,根据套筒节点的受力特点,在焊接球下半球施加固定约束,在对称面施加对称约束(图2).
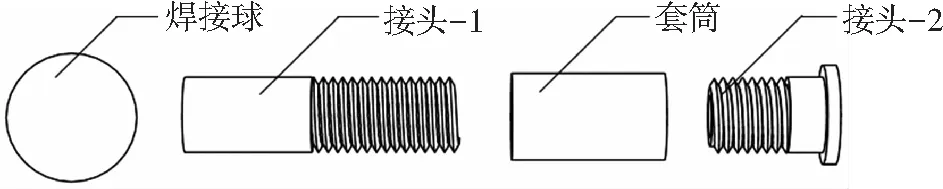
图1 套筒节点组成示意

图2 边界条件
由图1可知,由于安装需要,接头-1存在外露螺纹.为考察外露螺纹对节点承载力的影响,按考虑外露螺纹与否建立了图3(a)(方案1,不考虑外露螺纹)、图3(c)(方案2,考虑外露螺纹)所示两种模型.图3(a)、图3(c)为节点应力云图;图3(b)、图3(d)为螺纹接头部位应力云图.
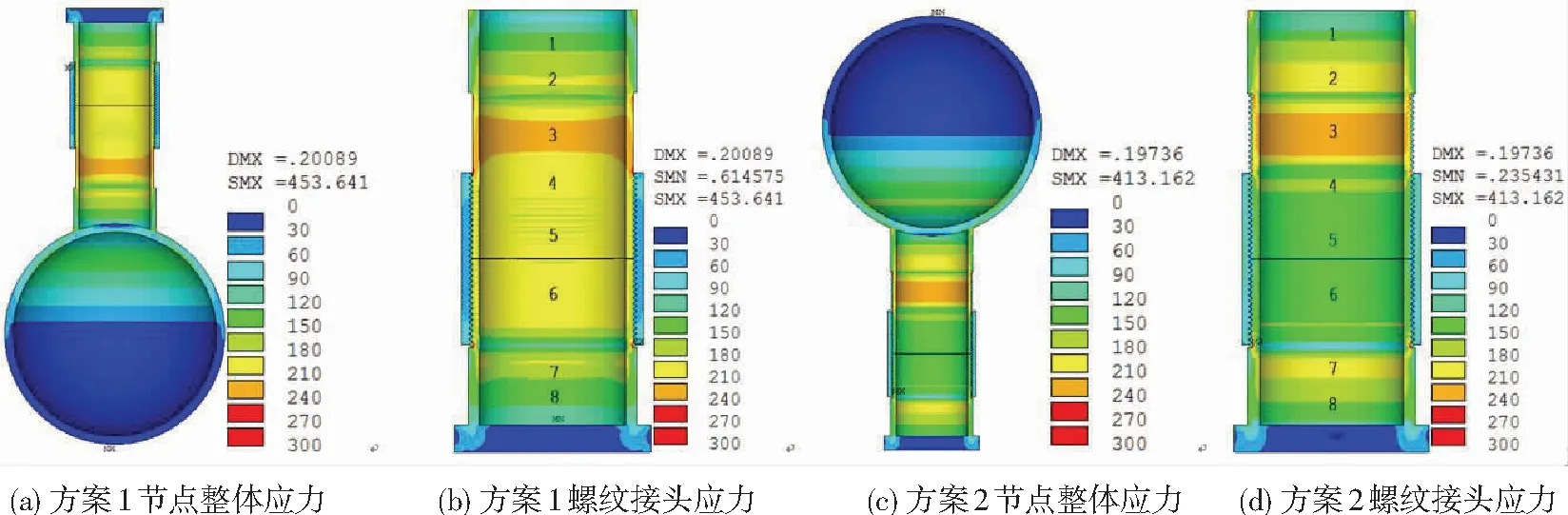
图3 模型方案1、2应力对比
从图3可看出:1) 方案1、2的应力分布规律基本一致,仅在外伸端稍有差异;2) 两个方案外伸端区域应力分布基本一致,但方案2在接头与套筒啮合区域应力稍大.表1提取并对比了两种方案部分关键点应力值,两者误差较小;3) 方案1中节点整体位移为0.201 mm,方案2为0.197 mm,相对误差为1.8%,误差较小,可忽略.因此,总体而言,两个方案计算结果基本一致,但方案1计算速度较快,因此节点分析采用图3(a)所示模型.

表1 方案1、2关键点应力对比
1.2 节点受压力学性能分析
由图3可知,节点受压状态下,焊接球区域应力值、变形值始终较小,对节点承载和变形影响较小,因此在本文分析中,未针对该部分展开.
图4(a)为一套筒节点算例的螺纹部位模型尺寸,外伸端螺纹连接区域的应力云图见图4(b),较大节点应力位于区域1~4.其中,区域1位于接头-1螺纹外露部分,由于该区域为节点壁厚最小处,因此整体区域应力值均较大;区域2为接头-1与套筒螺纹啮合区域的第一扣附近,啮合的前三扣区域应力值相对于其余螺纹区域应力值偏大,该区域为螺纹主要受力区域;区域3为接头-2与套筒螺纹啮合区域的第一扣附近,与区域2类似;区域4位于接头-2未车螺纹部分中部,应力相对较大.区域2和区域3两处应力因存在应力集中而导致其应力值较高,该问题是由于三角形螺纹建模中未采用倒角措施所致[18-19],实际应用时可采用倒角、改变螺纹深度等方式进行优化[20-21].因此,区域1处的应力值对节点整体性能影响较为关键.

图4 算例局部应力云图
从图4(b)可看出,在接头与套筒螺纹啮合区域,节点应力分布不均匀.接头应力分布规律为:应力分布从啮合区域的第一扣至最后一扣应力先减小后增大(图4(b)自上而下顺序);啮合区域第一扣和最后一扣应力值较大,承担了大部分轴力;啮合区域中部扣应力值较小,且分布均匀;每一扣螺纹均在牙根处应力较大.套筒应力分布规律为:套筒第一扣应力值较小,几乎不受力;第二扣(与接头啮合的第一扣)应力值较大;套筒自螺纹至外壁处,应力值逐渐降低,即套筒受力关键区域为螺纹牙处,壁厚增大对其套筒承载力提高影响较小;套筒其余变化规律与接头相同.
2 试验概况
2.1 试件设计
为验证节点数值分析模型可靠性,根据文献[13]结论,本文设计了两组试件,钢材强度等级为Q235B.母材材料性能试验测得其屈服强度为245 MPa,弹性模量为200 GPa.
第一组试件为轴压、偏压试件,由套筒、接头1、接头2、芯棒四部分组成.芯棒作用为避免加载时试件端部屈曲影响试验结果.试件及对照组参数如图5所示,安装后节点长170 mm(含芯棒).第二组试件为对照组,为管径20 mm,壁厚4 mm,长度为170 mm的圆管(含芯棒),其作用为对比和研究螺纹对圆管承载力的削弱幅度.轴压试件与偏压试件完全相同.

图5 试件尺寸及照片
2.2 试验装置及加载方案
试验设备采用万能材料试验机,为防止加载过程中试件失稳,在节点端部增加了约束端,见图6(a).偏压试验时,通过在约束端上部放置一枚钉子(图6(b)),施加偏心线荷载,偏心距为3 mm.试验采用静力单调加载,加载速率为2 mm/min(平均应变速率为0.000 2/s),分级施加,每加载5 kN间歇10 min.
试验依据横梁位移确定节点变形,并根据设备参数进行修正,通过绘制节点荷载-位移曲线,研究其抗压性能.

图6 试件及约束方法
3 轴压试验结果及对比分析
3.1 轴压承载力及试件破坏形态
图7(a)为3个轴压试件的荷载-位移曲线及破坏形态.由该图可知,3组试件的试验结果接近,试件弹性阶段承载力约为31 kN,对照组圆管承载力约为49 kN.节点外伸端承载力约为等直径、等壁厚圆管的63.2%,螺纹对圆管承载力削弱幅度为36.7%.图7(b)为试件破坏状态照片,节点破坏位置位于外露螺纹区域,呈屈曲破坏.节点破坏后仍较易拆卸,即套筒与接头螺纹啮合部分未发生塑性变形.
3.2 有限元分析结果与试验结果对比
为了验证有限元分析模型可靠性,依托上文有限元建模方法对两种试件进行数值模拟,模型材料参数为实测值,见图8.
图9为轴压试件的应力云图.图9(a)为模型局部应力云图,图9(b)为节点螺纹啮合区域云图.由图9(b)可知,节点应力最大区域为啮合第一扣的牙根处,剔除应力集中区域后,节点应力最大区域为外露螺纹段的中部(图9(a)),即该区域为节点的薄弱部位,与试验结果一致.
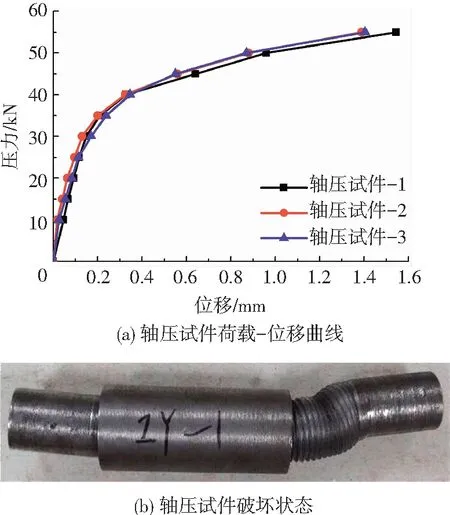
图7 试件轴压性能
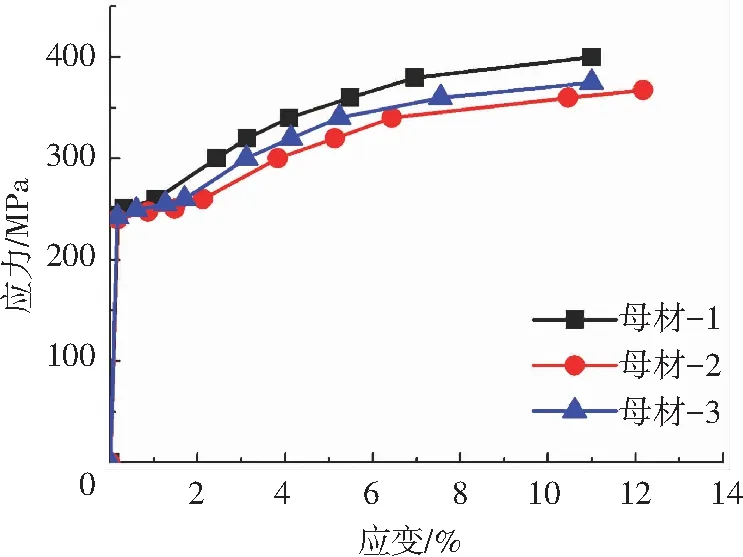
图8 母材材性试验曲线
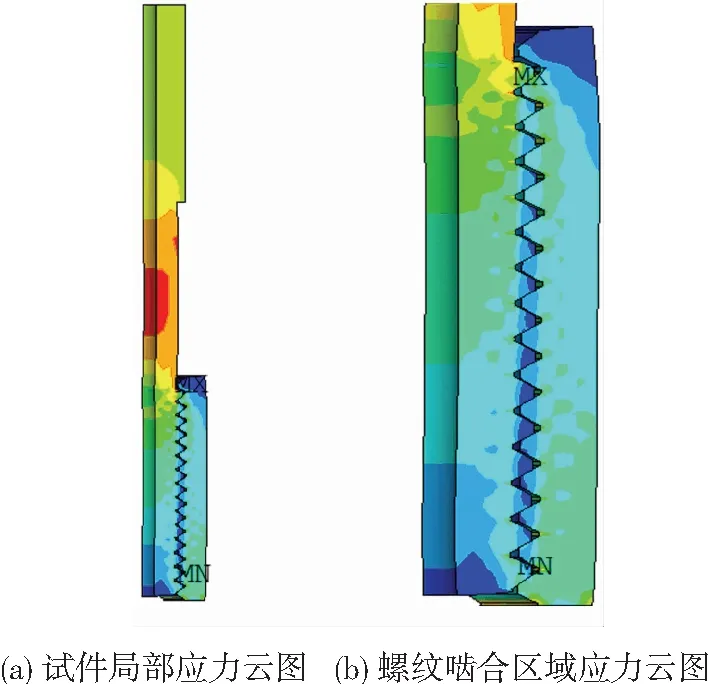
图9 轴压试件应力云图
图10为轴压试验结果与数值模拟的对比曲线.由图10可看出,在弹性阶段两组曲线吻合较好,承载力均为31 kN;在塑性阶段,试验结果略高于数值模拟.节点弹性阶段刚度方面,试验平均值为186 kN/mm,数值模拟值为165.6 kN/mm,模拟值较试验值低11%.误差的主要原因为螺纹摩擦力对节点承载力和刚度影响结果,数值模拟采用的是平均摩擦系数,而螺纹间的实际摩擦系数与加工精度、安装方法等因素密切相关,因此存在一定误差.
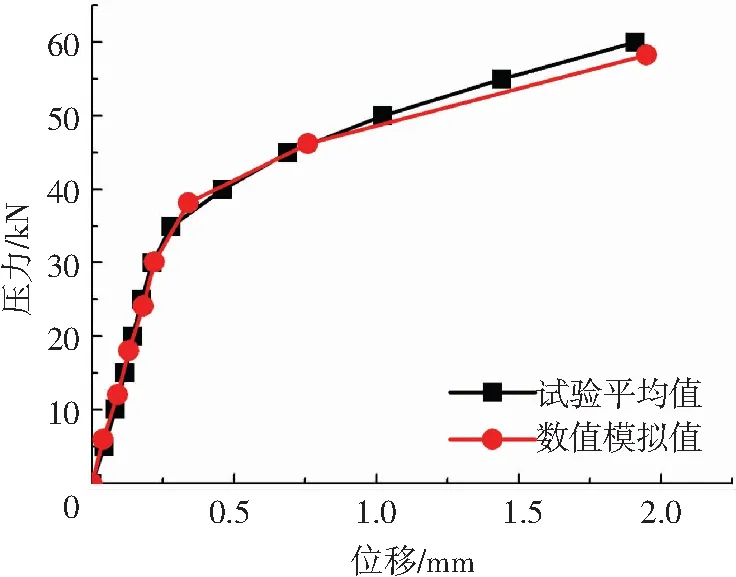
图10 轴压试验与数值模拟荷载-位移曲线对比
Fig.10 Comparison of load versus displacement curves for specimens and simulation model
4 偏心受压试验结果及对比分析
4.1 偏压承载力及试件破坏形态
图11(a)对比3个偏心受压试件与轴压试件的荷载-位移曲线.从图11(a)可知,3个偏压试件的试验结果较为接近,试件弹性阶段承载力约为26 kN,为轴压试件承载力的83.9%.试件破坏状态如图11(b)所示,与轴压试件基本一致,外露段屈曲破坏.

图11 试件偏压性能
4.2 有限元分析结果与试验结果对比
偏压试件分析模型局部应力云图见图12(a).模型参数设置及约束与轴压分析相同,不赘述.
由图12(a)可知,该模型应力最大区域亦为外露螺纹段中部,节点破坏情况与试验结果一致.图12(b)为试件荷载位移曲线与数值模拟结果对比.由该图可知,在弹性阶段两组曲线拟合较好,承载力均为29 kN左右,约为轴压试件的82%;在塑性阶段,数值模拟结果略高于试验结果.

图12 偏压试验与数值模拟对比
Fig.12 Comparison of specimens and simulation model under eccentric compression
5 外伸端抗压承载力理论分析
由于数值模拟方法计算量较大,不便应用于工程实际.为便于套筒节点工程应用,依托试验结果与数值模拟分析,本文对套筒节点螺纹外伸端抗压承载力和刚度的理论计算公式进行推导,以期建立便于工程应用的节点承载力计算公式.
5.1 计算假定
节点受压试验验证了数值模拟时将螺纹简化为水平锯齿状的合理性,即忽略螺纹螺旋升角的方法的可行性.数值模拟表明,节点仅在螺纹根部存在较大应力,壁厚区域应力较小.依托上述研究结论,理论分析时忽略螺纹小螺旋升角的影响,将一圈螺纹沿螺纹大径d展开,则螺纹牙可以等效为宽度πd的悬臂梁[22],见图13(a).套筒节点螺纹部分参数见图13(b).
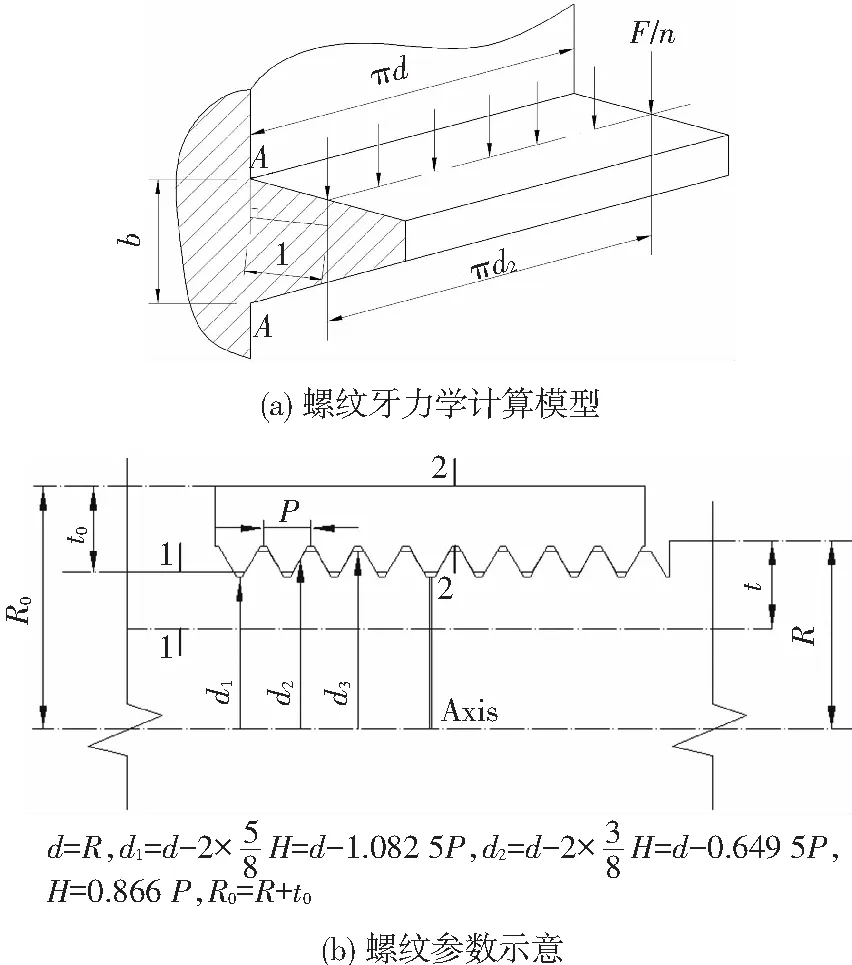
图13 螺纹牙力学计算模型
5.2 危险截面上的应力
螺纹联接在压力F的作用下,接头螺纹外露部分中螺纹牙根部为危险截面,该截面的有效工作面积为[22]
(1)
式中d1为螺纹小径,d2为螺纹中径.
危险截面上的拉、压应力σ为
(2)
当σ=σB时可得破坏荷载Fmax.
5.3 螺纹牙强度
在轴力F作用下,螺纹牙受到剪切和挤压作用.由于套筒和接头采用相同的材料,且内外螺纹强度相同,因此本文只考虑外螺纹牙的强度[22].假设每圈螺纹牙所承受的平均轴力为F/n,n为旋合扣数,并作用在以螺纹中径d2为直径的圆周上,则螺纹牙危险截面A-A(图13(a))上的剪应力τ为
(3)
式中b为螺纹牙根部处的厚度,对三角形螺纹b=0.87P,其中P为螺距.
螺纹牙危险截面的弯曲应力σb为
(4)

5.4 外伸端破坏形态
在实际工作状态下,套筒节点的螺纹外伸端可能出现的破坏形态有4种:1)螺纹外露段屈曲;2)螺纹牙剪切破坏;3)螺纹牙弯曲破坏;4)套筒破坏.下面分别对这4种状态下节点的承载力进行分析.
5.4.1 螺纹外露段屈曲
该破坏情况下,节点破坏位置为螺纹外露段最小截面处A1(图13(a)截面1-1),该截面应力为
(5)
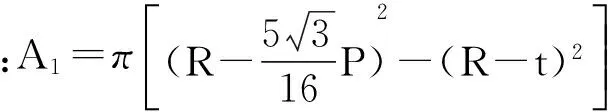
节点承载力为
(6)
式中[σ]为材料的许用正应力.
5.4.2 螺纹牙剪切破坏
该破坏情况下,节点破坏位置为螺纹牙底部最大截面处(图13(a)截面A-A),由式(3)可得节点承载力为
(7)
式中[τ]为材料的许用剪切应力,取[τ]=0.6σs.
5.4.3 螺纹牙弯曲破坏
该破坏情况下,节点破坏位置为螺纹牙底部最大截面处(图13(a)截面A-A),由式(4)可得节点承载力为
(8)
式中[σb]为材料的许用弯曲应力,在不考虑安全系数的情况下,取[σb]=σs.
易知F2 5.4.4 套筒破坏 该破坏情况下,节点破坏位置为套筒最小截面处A2(图13(b)截面2-2).该区域仅承受拉压荷载,其应力为 (9) 节点承载力为 (10) 令ΔA=A2-A1, (11) 由于t>P,且因螺纹加工工艺需要,套筒壁厚不会小于接头壁厚,即t0>t,则ΔA>0.即节点螺纹外露段必先于套筒发生破坏. 综上所述,节点破坏情况为螺纹外露段拉伸破坏和螺纹牙剪切破坏两种. 若节点螺纹外露段破坏,即F1 化简得 取系数 (12) 则节点抗压承载力计算公式为: (13) 结合文献[14]结论:当套筒壁厚与接头壁厚相等,螺距为杆件壁厚的1/2,进深为15倍螺距时,节点抗压承载力最大,式(13)可简化为 (14) 5.5 外伸端刚度 文献[23]提出螺纹旋合段等效弹性刚度计算公式为 (15) 结合套筒节点的特点,可将其外伸端分成6个并联的弹簧,见图14. 图14 外伸端刚度示意 外伸端的等效弹性刚度为 (16) 5.6 理论公式与试验结果对比分析 为验证理论公式的合理性,本文将轴压试件的参数和材料屈服强度代入式(14)和式(16),得到试验节点的弹性承载力和弹性刚度,并将计算结果与试验结果、数值模拟结果进行对比,见表2. 表2 公式、试验、模拟结果对比 由表2可知,弹性阶段承载力方面,公式结果与试验结果吻合较好,试验值和模拟值略低于公式值,相对误差为6.2%.误差来源主要有两方面:1)螺纹的悬臂梁模型为近似模型,该模型求得的节点承载力会略高于实际值;2)理论公式采用屈服强度计算节点承载力,而节点试验所得荷载-位移曲线无明显屈服过程,承载力读取时可能偏小.由于公式值高于试验值和模拟值,因此后续将补充大量数值模拟和部分试验,引入修正系数,对理论公式进行修正. 弹性刚度方面,试验值和模拟值低于公式计算值,误差相对较大,为9%,原因在于公式(15)为经验公式,本身存在一定的误差,且试验中螺纹会出现滑移现象,该现象无法在试验中观测,导致实测位移偏大,刚度偏小.试件-1偏差较大,可能为试件安装时存在一定间隙,导致该试件实测位移偏大. 通过节点抗压试验研究并结合数值模拟与理论分析,对套筒节点受压力学性能进行研究,得到以下结论: 1)套筒节点受力性能较好,轴压时其承载力约为等直径、等壁厚圆管的63.2%;当存在较大偏心时,节点偏压承载力约为轴压的83.9%. 2)数值模拟得到的节点抗压性能与试验结果吻合较好,节点分析模型合理、可靠. 3)通过理论分析得到节点外伸端抗压承载力计算公式,并通过试验验证了该公式的正确性,为该节点的应用提供依据. [1] 范峰, 马会环, 张洋, 等.碗式半刚性节点网壳弹塑性稳定分析[J]. 哈尔滨工业大学学报, 2010, 42(10):1513-1518. FAN Feng, MA Huihuan,ZHANG Yang, et al. Elasto-plastic analysis on single layer reticulated domes with soket-joint system [J]. Journal of Harbin Institute of Technology, 2010, 42(10):1513-1518. [2] 范重, 杨苏, 栾海强. 空间结构节点设计研究进展与实践[J]. 建筑结构学报, 2011,32(12): 1-15. DOI: 10.14006/j.jzjgxb.2011.12.003. FAN Zhong, YANG Su, LUAN Haiqiang. Research progress and practice of design of spatial structure joints[J]. Journal of Building Structures, 2011,32(12): 1-15. DOI: 10.14006/j.jzjgxb.2011.12.003. [3] 丁芸孙. 网(壳)架及轻钢结构设计、施工及检验的有关问题探讨(上)[J].空间结构, 2004,10(1):31-40. [4] DING Yunsun. Discussion on design, construction and inspection of space grid structures and light-weight steel structures (Part I)[J]. Journal of Building Structures, 2004, 10(1):31-40. [5] 王剑锋, 刘锡良, 陈志华. 新型装配式四角锥网架结构体系的分析和研究[J]. 工程力学, 1999(增1): 810-815. WANG Jianfeng, LIU Xiliang, CHEN Zhihua.Analysis and research of the new assembly four square pyramid space grid structure[J]. Engineering Mechanics, 1999(s1): 810-815. [6] 严慧, 罗尧治, 赵阳. 一种新型预制四角锥网架结构的分析与应用研究[J]. 建筑结构, 2002, 32(3):51-54. YAN Hui, LUO Yaozhi, ZHAO Yang, et al. Analysis and research of the light-weight space truss consisting of prefabricated pyramidal units[J]. Building Structure, 2002, 32(3):51-54. [7] CHANS D O, CIMADEVILA J E, GUTIÉRREZ E M. Strength of joints with epoxy-glued threaded steel rods in tali timber [J]. Journal of Materials in Civil Engineering. 2011, 23: 453-458. DOI: 10.1061/(ASCE)MT.1943-5533.0000191. [8] SHI Gang, BAN Huiyong, BAI Yu, et al. A novel cast aluminum joint for reticulated shell structures: experimental study and modeling [J]. Advances in Structural Engineering. 2013, 16(6):1047-1059. DOI: 10.1260/1369-4332.16.6.1047. [9] FAN Feng, MA Huihuan, CAO Zhenggang, et al. A new classification system for the joints used in lattice shells [J]. Thin-Walled Structures. 2011, 49: 1544-1553. DOI: 10.1016/j.tws.2011.08.002. [10]FAN Feng, MA Huihuan, CHEN Gengbo, et al. Experimental study of semi-rigid joint systems subjected to bending with and without axial force [J]. Journal of Constructional Steel Research, 2012, 68: 126-137. DOI: 10.1016/j.jcsr.2011.07.020. [11]FAN Feng, WANG Minling, CAO Zhenggang, et al. Seismic behaviour and seismic design of single-layer reticulated shells with semi-rigid joint system [J]. Advances in Structural Engineering, 2012, 15(10): 1829-1841. DOI: 10.1260/1369-4332.15.10.1829. [12]曹正罡, 陈哲明, 万宗帅, 等. 80m球径螺栓球节点单层球面网壳稳定性能分析[J]. 哈尔滨工业大学学报, 2015,47(6): 1-8.DOI:10.11918/j. issn.0367-6234.2015.06.001 CAO Zhenggang, CHEN Zheming, WANG Zongshuai, et al. Analysis of stability of 80 m diameter single-layer reticulated dome with bolt-sphere joints [J]. Journal of Harbin Institute of Technology, 2015,47(6): 1-8.DOI:10.11918/j. issn.0367-6234.2015.06.001 [13]李思遥, 李雄彦, 姚玄一, 等. 对接套筒丝扣节点轴向受力性能分析[J]. 建筑钢结构进展, 2014,16(5): 18-28. LI Siyao, LI Xiongyan, YAO Xuanyi, et al. The axial mechanical properties of butt threaded-sleeve cast steel connection [J]. Progress in Steel Building Structures, 2014,16(5): 18-28. [14]李思遥, 李雄彦, 薛素铎. 套筒式节点受拉力学性能试验及有限元分析[J]. 工业建筑, 2015(1): 23-26,65.DOI: 10.13204/j.gyjz201501004. LI Siyao, LI Xiongyan, XUE Suduo. Experimental and finite element research on threaded-sleeve connection in tension [J]. Industrial Construction, 2015(1): 23-26,65.DOI: 10.13204/j.gyjz201501004. [15]CHEN Ji. Stability of steel structures theory and design [M]. Beijing: Science Press, 2010:13-15. [16]TANAKA M, MIYAZAWA H, ASABA E, et al. Application of the finite element method to bolt-nut joints-fundamental studies on analysis of bolt-nut joints using the finite element method [J]. Bulletin of the JSME, 1981, 24(192): 1064-1071. [17]高连新, 金烨. 套管连接螺纹的受力分析与改善措施[J].上海交通大学学报, 2004, 38(10): 1729-1732. GAO Lianxin, JIN Ye. The load analysis and betterment of casing connections[J]. Journal of Shanghai Jiaotong University, 2004, 38(10): 1729-1732. [18]LEHNHOFF T F, BUNYARD B A. Bolt thread and head fillet stress concentration factors [J]. Journal of Pressure Vessel Technology, Transactions of the ASME, 2000, 122(2): 180-185. [19]ZHAO Hua. Analysis of the load distribution in a bolt-nut connector [J]. Computers & Structures, 1994, 53(6): 1465-1472. DOI: 10.1016/S0142-1123(98)00036-X. [20]DRAGONI E. Effect of thread pitch and frictional coefficient on the stress concentration in metric nut-bolt connections [J]. Journal of Offshore Mechanics and Arctic Engineering, 1994,116(1):21-27. [21]FUKUOKA T. Evaluation of the method for lowering stress concentration at the thread root of bolted joints with modifications of nut shape [J]. Journal of Pressure Vessel Technology, Transactions of the ASME, 1997, 119(1): 1-9. [22]段巍, 温新林, 唐贵基, 等. 不同旋合扣数下钢拉杆螺纹联接强度试验及有限元应力分析[J]. 机械强度, 2008, 30(5): 823-828. DUAN Wei, WEN Xinlin, TANG Guiji, et al. Strength test and fembased stress analysis of threaded connection for steel tie rod under different connection rounds[J]. Journal of Mechanical Strength, 2008, 30(5): 823-828. [23]山本晃. 螺纹联接的理论与计算[M]. 郭可谦, 译. 上海: 上海科学技术文献出版社, 1984. Akira Yamamoto. Theory and calculation of screw thread connection[M]. GUO Keqian (trans.). Shanghai: Shanghai Scientific and Technological Literature Press, 1984. (编辑 赵丽莹) Compression performance of threaded-sleeve connection LI Siyao1, LI Xiongyan1, XUE Suduo1, YE Jihong2 (1.Key Laboratory of Urban Security and Disaster Engineering (Beijing University of Technology), Ministry of Education,Beijing 100124, China; 2.Key Laboratory of Concrete and Prestressed Concrete Structures (Southeast University),Ministry of Education, Nanjing 210018 , China) The threaded-sleeve connection (TSC) is a new type of connection for grid structure, of which the key part situates at the threaded extended end. The simulation models of TSC were established and compared by ANSYS. The compression mechanical property and stress distribution were analyzed firstly. The performance of compression and eccentric compression were tested through experiments. The simulation results were compared with test data to verify the correctness of the FE model. Based on the simulation and experimental results, the theoretical formulas of compression capacity and stiffness of the extended end were developed. It is illustrated that the capacity of TSC under compression is about 63.2% of that of the pipe with same material, diameter and wall thickness. When subjected to large eccentricity, the capacity of TSC decreases to about 83.9% of the axial compressive capacity. The failure form of the specimens under compression or eccentric compression is the buckling of the extended threads. The simulation results agree well with the test results, which illustrates the effectiveness of the FE method, and the theoretical results are also in good agreement with the test data. The TSC shares good compression performance, and the most weakness area exists in the extended part of the threads, the buckling of which will lead to the failure of the connection. thread-sleeve connection; compression property; finite element analysis; experiment 10.11918/j.issn.0367-6234.2016.12.008 2015-06-07 国家自然科学基金(51578019);北京市自然科学基金(8152006);城市与工程安全减灾教育部重点实验室&工程抗震与结构诊治北京市重点实验室重点项目(USDE201401) 李思遥(1990—),男,博士研究生; 薛素铎(1959—),男,教授,博士生导师; 叶继红(1967—),女,教授,博士生导师 李雄彦,xiongy2006@126.com TU393.3 A 0367-6234(2016)12-0062-08





6 结 论

