纤维增强树脂基复合材料阻尼性能的研究进展

刘涛

(辽宁省产品质量监督检验院，沈阳110144)

纤维增强树脂基复合材料阻尼性能的研究进展

刘涛

(辽宁省产品质量监督检验院，沈阳110144)

树脂基复合材料的阻尼性能同其力学性能一样具有各向异性行为，对阻尼性能有一定要求的结构和产品，应依据一定的方法进行设计和分析。本文对树脂基复合材料的阻尼性能的分析方法进行了阐述和总结，列举了国内外专家学者在该领域进行的主要研究成果，从阻尼的定义、阻尼性能的分类到复合材料阻尼的微观和宏观力学分析方法，进行了介绍。对复合材料结构和产品的阻尼设计起到了一定的借鉴作用。

树脂基复合材料;阻尼;微观力学;宏观力学

1 引言

纤维增强树脂基复合材料具有比强度高、比刚度大、可设计性强、抗疲劳性能好、耐腐蚀性能优越和便于大面积整体成型等显著优点，显示出比传统钢、铝合金结构材料更优越的综合性能，已经成为我国及一些世界强国重点研究发展的新型材料。纤维增强树脂基复合材料日益广泛地应用于航空航天等现代高科技领域，成为继铝合金、钢、钛合金之后的第四大航空结构材料，其用量成为航空航天结构的先进性标志之一。纤维增强树脂基复合材料在舰船、汽车工业、建筑、医疗及运动器械等领域中也有着广泛的应用。

随着新型民用超音速飞机、核潜艇、高速列车及汽车的飞速发展，机械设备趋于高速、高效和自动化，但是振动、噪声和冲击等带来的影响也越来越突出。振动和噪声能严重破坏仪器设备运行的稳定性和可靠性，是导致运行控制精度下降、结构产生疲劳损伤、安全使用寿命缩短等结果的直接原因，并且污染环境，危害人们的身心健康。因此，减振降噪，提高材料的阻尼性能，改善人机工作环境是一个亟待解决的问题。

纤维增强树脂基复合材料不仅具有高比强和高比模，而且具有粘弹性的特点，其阻尼更是比普通金属材料高10～100倍。阻尼性能作为树脂基复合材料及其结构动力学性能的一项重要指标，不但在控制结构的振动和噪声方面，而且在延长结构承受循环载荷和冲击的服役时间方面都扮演着重要的角色。因此，揭示纤维增强树脂基复合材料宏观能量耗散产生的内在机制，建立复合材料阻尼性能定量预测的理论与方法，根据工程需要选择合适的组分材料，设计阻尼性能优异的树脂基复合材料，这些方面的纤维增强树脂基复合材料阻尼研究工作，从理论和实践两方面都具有重大的现实意义。

2 国内外复合材料阻尼性能研究进展

2.1 国外研究进展

20世纪60年代起，国外以石墨/环氧、Kevlar/环氧等树脂基复合材料为主，从理论上研究了树脂基阻尼复合材料的阻尼机理、阻尼测量以及基体树脂、固化剂、纤维的铺设方式、纤维种类、复合材料结构等对其阻尼性能的影响，取得了较好的研究成果。

Sehultz＆Tsai，Hashin及Adams等人［1-5］对复合材料的阻尼进行了开创性的研究工作，将对应原理和应变能法应用于复合材料阻尼性能的分析预测。这两种方法对复合材料有着广泛的适用性。

Ni等［6］认为正交各向异性复合梁的阻尼是材料方向的函数，并且分析了正交层板、斜交层板以及更多普通类型对称层板的阻尼性能。

Lin等［7］和Maheri等［8］运用有限元(FEM)分析评价了无约束纤维增强板的阻尼特性。这些分析包括两个横向剪切阻尼参数。Saravanos和Pereira［9］运用离散层板理论开发了夹层复合材料层板阻尼模型。Cupial和Niziol［10］运用一阶剪切变形理论测定具有粘弹性内层的矩形三层板的损耗因子。Berthelot和Sefrani［11］运用Ritz法来描述单向板的阻尼特性。

Liao等［12］分析了单向和对称斜交层板以及将对称的聚乙烯-丙烯酸(polyethylene-co-acrylic acid，PEAA)铺层交织在层合板中间面的阻尼行为。Yim［13］和Yim＆Jang［14］将Adams＆Bacon模型应用于不同类型的层板。Yim和Gillespie［15］进一步研究包括在0°和90°情况下单向层压板横向剪切效应。

Yihua等［16］利用各项异性层压阻尼板理论研究复合材料夹层损耗因子的控制机制。Berthelot［17］进一步对层合板进行了阻尼分析，并且运用Ritz法建立正交各向异性粘弹性交织复合材料的阻尼模型，用来分析矩形板的弯曲振动。最近，Suzuki等［18］基于多层板理论和高阶理论，提出了具有粘弹性铺层的层合板的自由振动和阻尼分析的有限元模型。

Finegan等［19］通过系统分析方法研究了经过特殊处理后的纤维填充高聚物网络体系的阻尼性能，发现在纤维表面涂覆高耗能的涂料可以提高材料的阻尼性能，并通过有限元分析研究了频率、温度、涂层厚度对材料阻尼性能的影响。

Hajime等［20］将碳纤维填充到环氧树脂体系基体，复合材料不仅具有很高的硬度，而且阻尼效果明显增大，阻尼性能和力学性能不仅取决于弹性体的粘弹性，而且还与碳纤维的层合排列方式有关。

国外学者对夹层(Sandwich)材料作了大量的研究工作，并运用弹性-粘弹性对应原理，提出了复数模量的概念。复数模量的实数部分代表弹性刚度，虚数部分则与能量耗散有关。Fujimoto等［21］在研究碳纤维增强(CFRP)/阻尼材料薄板结构时，由单向碳纤维、环氧树脂、聚乙烯组成的夹层结构，其内耗值比传统的CFRP高5～50倍，并且其值可以根据需要进行设计。最近，Meunier和Shenoi［22］将复数模量概念与高阶剪切变形理论联系起来，建立夹层板的阻尼模型。Plagianakos和Saravanos［23］提出了预测厚复合材料和夹层板模态阻尼的有限元分析。Assarar等［24］基于夹层板理论，运用有限元分析模拟夹层材料的阻尼。将获得的结果与实验结果进行对比，并分析了不同的因素对夹层材料阻尼的影响。

2.2 国内研究进展

相对于国外的研究，我国在阻尼材料领域起步较晚，但也取得了一些成果。西安航天复合材料研究所的廖英强等［25］研究了树脂、纤维及其纤维增强复合材料的阻尼性质，利用体积混合率法则对混杂纤维增强复合材料的阻尼性质进行了分析，结果表明混合率法则在复合材料的阻尼研究过程中是一个有效的方法，为相关领域的研究工作指明了方向。

秦东奇等［26］认为云母的加入可使IPN阻尼材料内部形成微观强制层，在剪切力作用下，有取向的趋势，增大了聚合物链与云母片的摩擦，增强了阻尼性能。同时在PU/PMMA IPN阻尼材料中分别加入10%的玻璃棉和直径为10～100 μm的微球，得到的阻尼因子tanδ≥0.5的温域达到110℃。

钱军民等［27］以聚合物和无机纤维为原料，用化学发泡法制得了新型泡沫阻尼吸声材料，在中、低频范围内具有优异的阻尼吸声性能。

晏雄等［28］用具有压电、介电效应的有机材料替代无机压电陶瓷，在高分子材料氯化聚乙烯(CPE)中，填充导电的气相成长超细碳纤维和具有强介电性能的N，N-二环己基-2-苯并噻唑基亚磺酸胺，制备导电压电型阻尼材料。研究表明，当导电网络形成时，材料的阻尼效果较好，因为这时复合材料内部的能量损耗主要是靠振动机械能→电能→热能的转换损耗来实现的。

李明俊等［29］将各向异性设计引入层合阻尼结构中，从理论上分析了各向异性层合阻尼结构的阻尼特性及其控制机理。从而验证了建立约束阻尼层合结构各向异性优化设计新体系的可行性。分析研究表明，内部柔性层对阻尼性能的影响要比应力耦合对其影响大得多;在高于基本模式的固有频率下，能显著地提高损耗因子。

孙大刚等［30］解决了多层阻尼减振结构中参数之间互为耦连的难题，研究了粘弹性阻尼材料的温度-频率动态特性，并把其特性曲线拟合成方程，建立了结构的优化模型。

杨雪等［31］制备了多层阻尼复合结构，应用有限元方法对多层复合结构阻尼性能进行了理论研究。计算结果与实验结果基本一致。利用该有限元模型分析了各层阻尼材料的几何及物理参数对复合结构阻尼性能的影响。分析表明:阻尼材料的厚度、损耗因子和弹性模量对阻尼复合结构阻尼性能有较大影响，而阻尼材料的密度对阻尼复合结构阻尼性能的影响不明显。

虽然国内在复合材料阻尼性能研究方面已经有了较大发展，但在提高阻尼预测的精度、粘弹性结构在复合材料中的应用及三维多向编制复合材料阻尼性能预测等方面，还有复合材料如何在实际工程中有效的应用方面仍然需要进行大量的课题研究。

3 阻尼的定义及表征

3.1 阻尼的定义

阻尼(Damping)，指由于材料内部原因而使振动机械能消耗的现象，又称内耗(Internal friction)，其基本定义为:

式中，W为振动一周的总能量，ΔW为能量损耗，Q为振动品质因子。

阻尼是振动系统损耗能量能力的一个标志，受频率、温度、振动幅值等因素的影响较大。对阻尼性能的研究包括材料阻尼和结构阻尼两个方面。

3.2 阻尼性能的表征

为了进一步量化材料的阻尼性能，人们一般选用相位角正切值(tanδ)、品质因子的倒数(Q-1)、对数衰减率(φ)、比阻尼能力(ψ)、吸声系数(α)等对其进行表征，各个表征参量的含义、数学表达式及特点如表1所示。

对阻尼材料振动阻尼性能的研究目前用到的主要有以下三种方法:一是动态力学热分析法，使用粘弹谱仪(Dynamic Mechanical Analyser，DMA)获取材料的储能模量、损耗模量，进而计算出材料的损耗因子(tanδ)［32］;二是悬臂梁法［33］;三是差示扫描量热分析法(Differential Scanning Calorimetry，DSC)。

在这三种方法中最常用的是动态力学热分析法。动态力学热分析是一种发展很快、应用极广的热分析技术，按照ICTAC定义:DMA是在程序控温下，测量物质在振动负荷下的动态模量和力学损耗与温度关系的技术。DMA能直接给出阻尼材料的E'～T、E″～T及tanδ～T的关系曲线，对聚合物的玻璃化温度、交联、相分离及分子聚集态结构很敏感，是研究高聚物阻尼性能的一种有效而简便的手段。

根据DMA测试，阻尼性能的表征有2种方法:

(一)用tanδ-T曲线下的面积(TA)表示;

表1 阻尼性能的表征参量

(二)用E″-T曲线下的面积(LA)来表示。

TA与LA直接决定了阻尼材料的阻尼性能，TA或LA越大，阻尼能力越强。阻尼性能通常从内耗峰的高度和跨越温度范围来加以评价。阻尼系数tanδ为E″与E'之比，通常tanδ＞0.3的温度范围(ΔT)表示阻尼材料的有效阻尼温度区域，tanδ值越大，tanδ＞0.3的温度范围越大，材料的阻尼能力越大。

4 材料阻尼与结构阻尼

4.1 聚合物基复合材料阻尼性能

聚合物基阻尼复合材料是用纤维增强具有一定力学强度和较高损耗因子的聚合物而形成的复合材料。增强相有Kevlar(芳纶)纤维、碳纤维和玻璃纤维等。

复合材料的阻尼机理完全不同于传统的金属材料与合金。纤维增强复合材料的能量损耗机理有所不同［34］:

(1)基体和纤维材料的固有粘弹性:复合材料的主要阻尼来源于基体。但是，碳纤维和Kevlar纤维相比其他纤维而言，材料本身阻尼较高，因此分析时必须考虑它们的阻尼。

(2)界面引起的阻尼:界面是指临近纤维表面，具有一定厚度的区域，它具有与纤维和基体不同的性质。界面性能的强弱不仅影响纤维增强复合材料的力学性能而且影响它的阻尼。

(3)由材料破坏引起的阻尼:主要包括以下两个方面:第一，由于纤维和基体之间界面非粘合区域的滑动或分层引起的摩擦阻尼;第二，由于基体开裂或纤维断裂等带来的能量耗散引起的阻尼。

(4)粘塑性阻尼:在大振幅/高应力情形下，特别是热塑性复合材料，由于在纤维之间的局部区域内存在高应力和应变集中而表现出非线性的阻尼特性。因此在明显低于复合材料的弹性极限下也应重视材料的弹塑性微观力学行为。

(5)热弹性阻尼:是由从复合材料压应力区域到拉应力区域的循环热流动而引起的。

通常认为复合材料的阻尼主要来源于基体材料的粘弹性以及增强纤维与基体界面间的滑移。

根据复合材料的体积混合率法则，对单向铺层复合材料沿纤维方向的复弹性模量可以表示为纤维复弹性模量和基体复弹性模量的函数:

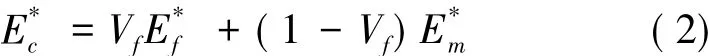
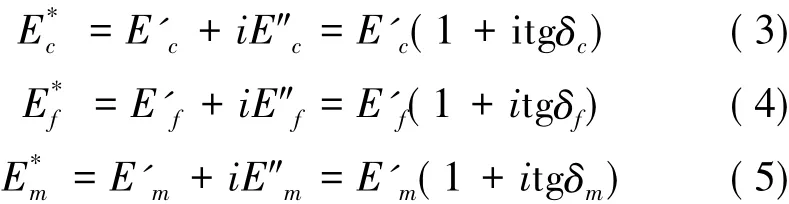
其中:tgδc:复合材料的弯曲阻尼;tgδf:纤维的阻尼;tgδm:基体的阻尼。

将tgδc、tgδf、tgδm带入混合率公式中，可以得出单层铺层复合材料沿纤维方向的弯曲阻尼:

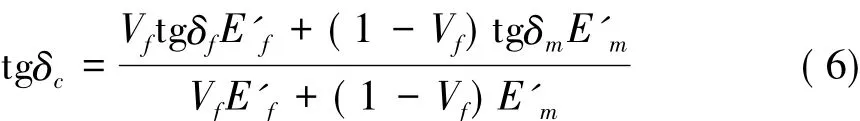
4.2 结构阻尼

阻尼材料在使用结构上通常有两种处理方式，如图1所示。一种是自由阻尼(或扩展阻尼)，即直接将阻尼材料粘附到需要作减振处理的结构件表面上，当结构件弯曲振动时，通过阻尼层材料的拉伸形变来消耗能量;另一种是约束阻尼，即在阻尼层上再粘附一层高模量的刚性约束层材料，当结构件弯曲时，通过阻尼层材料的剪切形变来消耗能量以达到减振降噪作用。

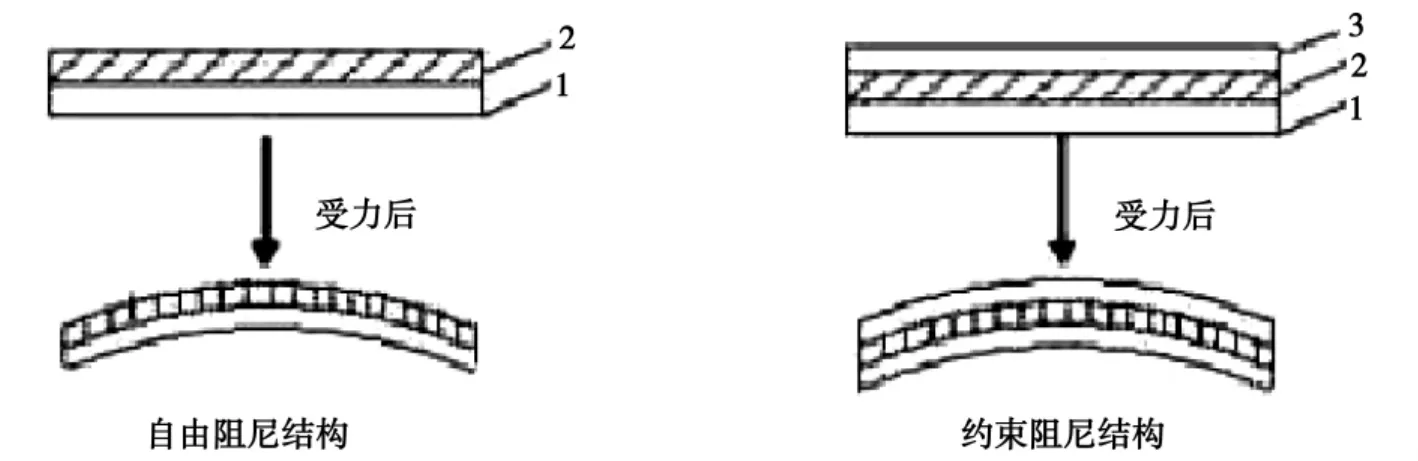
图1 阻尼结构示意图1—结构件;2—阻尼层;3—约束层

自由阻尼层合结构系统的损耗因子与阻尼材料的性质以及结构材料的性质密切相关，并且还与结构层厚度、阻尼层厚度等因素有关，但是理论与试验均表明该结构在低频时效果比较差。自由阻尼处理的理论分析方法主要有三种:复刚度法、应变能法、模态分析的有限元法。

约束阻尼结构尤其是各向异性层合的约束阻尼结构，其结构在振动的过程中，阻尼层材料不同的部分分析受到剪切和拉伸应变的量不同，是其有很大的能量损耗，因而该结构损耗因子在一定的温度范围和频率范围内有了很大的提高。但是该方法最大的局限性是在弯曲和复杂的表面上应用较为困难。

结构阻尼作为复合材料及其结构动力学中一个重要的参数，在振动、噪声控制领域都有十分重要的应用。对于复合结构的阻尼性能，近年来已经有了很大进展，但是如何在实际工程中有效地应用仍是一个需要大量研究的课题。

5 阻尼性能的分析预测方法

5.1 宏观力学方法

早在1973年，Adams和Bacon建立了单向纤维增强复合材料宏观力学阻尼模型，这个模型被称为Adams-Bacon准则。根据准则，单向复合薄层板的能量消耗是由纵向应力、横向应力和剪应力引起的能量消耗的总和。此模型可用于玻璃纤维和碳纤维增强复合材料的单向偏轴、正交铺层、角度铺层和一般铺层的阻尼性能预测。

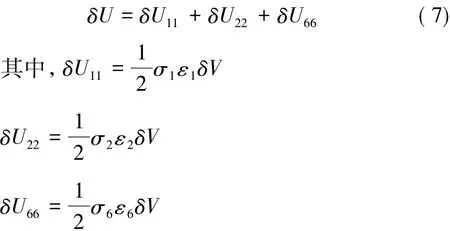
δU11表示纵向载荷储能应变;δU22表示横向载荷储能应变;δU66表示剪切载荷储能应变。

Adams和Maheri结合Adams-Bacon准则，运用单向复合材料的基本弹性关系，预测各向异性CFRP和GFRP梁在不同纤维取向的模量和弯曲阻尼。并且分析了长径比和应力对阻尼的影响。

McIntyre和Woodhouse运用近似的薄板弯曲理论研究正交层板的动态特性，在任何频率下其线性振动性能都是四个弹性和四个阻尼常数的函数。试验证实阻尼和频率有着非常好的可预测性。

Talbolt等以经典层合板理论为基础，用复模量法和应变能法研究了层合板的力学和阻尼特性，由各个单层的弹性常数和阻尼常数推导了层合板的阻尼常数。用该方法预测的层合板阻尼常数能达到大多数工程应用所要求的精度，应用该模型还可以反推单层的弹性常数和阻尼常数。

Crane和Gillespe基于经典层合理论，采用复弹性模量法研究了复合材料的宏观阻尼特性，分析得到了材料的纵向、横向和剪切损耗因子，并揭示了损耗因子和频率的关系。结果表明，非对称层合结构的应力耦合对损耗因子也有影响，损耗因子随弯矩耦合项的增大成比例地增大，而且在15°、30°的纤维铺设角范围内增加得非常大。

Barkanov和Gassan运用复刚度法和层合理论建立了FEM/频率相关模型用来分析复合层合梁的阻尼。通过复合特征区间和指定响应频率的方法，石墨环氧复合材料的损耗因子具有很好的一致性。

上海交通大学的范永忠等认为玻璃纤维GF和碳纤维CF混杂复合材料中两种纤维对阻尼性能和力学性能的作用和贡献是不同的，玻璃纤维复合材料的阻尼性能比碳纤维复合材料的要好许多。GF/ CF混杂复合材料的阻尼性能符合混合率，阻尼因子界于GF复合材料和CF复合材料的之间。玻璃纤维在外层时，复合材料的阻尼性能高于玻璃纤维在内层时的情况。玻璃纤维和碳纤维混杂复合材料的阻尼性能和力学性能中两种纤维的作用和贡献是不同的。从材料设计的角度来说，混杂纤维种类、方式、含量的选择与设计对兼顾最终复合材料的力学性能和阻尼性能是起决定性的。

李明俊等分别从理论上和通过大量的试验分析了各向异性约束层合阻尼结构的阻尼特性、各相关因素对其结构损耗因子的影响规律及其控制机理，得出了一些结论:各向异性层合阻尼板靠近阻尼层的柔性层设计有助于结构损耗因子的提高;保持各向异性层合板的总厚度不变，增加中间阻尼层的厚度会引起阻尼损耗因子的上升，特别是对较低固有频率的损耗因子提高的非常有效;将各向异性引入阻尼复合结构中可使结构损耗因子适应更复杂的设计要求，但不能一味增强柔性层，还要受到结构刚度的限制。

复合材料宏观力学阻尼预测研究中的影响因素有:纤维排列方向，层合结构，频率和应力的阻尼特性。常用的阻尼分析方法有:对应原理，应变能(SE)法和SE/FEM法。

5.2 微观力学方法

利用微观力学方法能够建立复合材料的宏观阻尼特性与其组分材料的粘弹性和阻尼性能及微观结构之间的定量关系，有利于分析纤维含量、纤维和基体自身的粘弹性和阻尼性能、增强纤维长径比、纤维取向、界面条件和中间相等对复合材料阻尼性能的影响。

White和Abdin研究表明在合适的纤维长径比和体积分数的情况下，直列短纤维增强复合材料的阻尼有所提高，并且能保持较高的刚度。在假定不能忽视损耗因子的情况下，储存和损耗模量可用Cox模型来预测。试验测得CFRP损耗因子比理论值要高，这主要由于分析模型中没有考虑到材料的动态行为，如:纤维相互作用的影响，纤维和基体界面的粘着度，简支梁的剪切变形程度还有纤维末端的实际应力要比预计值高很多。而且，CFRP的杨氏拉伸模量不同于压缩模量。Willway和White运用混合原理和Cox模型(考虑到非连续纤维的影响)对单向CFRP的纵向弯曲阻尼进行了理论研究。并且，假定只有树脂基体消耗能量的情况下，运用材料力学方程和对应原理可计算出连续纤维增强复合材料的横向弯曲和横向剪切阻尼。理论和试验结果证实用高耗能的树脂基体可以生产出具有高纵向模量和损耗因子的单向CFRP层板。

Chang和Bert运用微观力学对单一铺层纤维增强复合材料进行了完整的阻尼和刚度特性分析。损耗角正切的预测是基于弹性-粘弹性对应原理(对刚度用显式表达)和能量法。对硼-环氧树脂，硼-铝，E玻璃-环氧树脂的刚度和损耗角正切的分析结果与实验值比较吻合。

Kaliske和Rother采用Aboudi的自洽单胞体元近似理论建立了复合材料阻尼计算模型。模型是由一个纤维单元和三个基体单元组成的体积元(图2)。

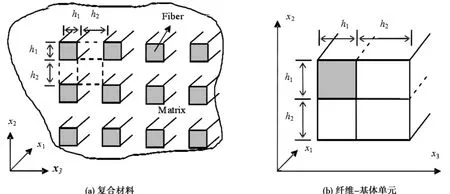
图2 Kaliske模型体积元

在假设纤维和基体为线性粘弹性的基础上，根据纤维和基体的耗能特性和力学特性推导了复合材料的六个阻尼损耗因子:

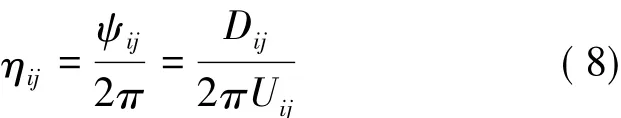
Dij:体积元一个振动周期内耗散的能量;Uij:体积元在振动内存储的最大应变能。

Hwang等引用典型体积元模型，并引入第三相组分材料——纤维/基体界面相，根据应变能法和有限元法研究了在纤维轴向载荷、纤维横向载荷、面内剪切载荷和面外剪切载荷作用下体积元的阻尼和模量，重点考察了界面相尺寸对复合材料阻尼的影响。材料的阻尼损耗因子可以表示为各组分应变能和阻尼损耗因子的函数:

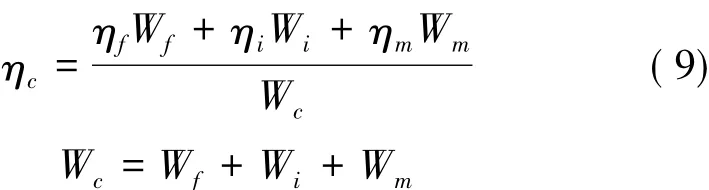
式中，Wc为复合材料总应变能，Wf为纤维中的应变能，Wi为界面相中应变能。

Saravanos和Chamis采用了方形单纤维典型体积元模型(图3)。利用微观力学方法预测了单向纤维增强复合材料的阻尼损耗因子，模型综合考虑了基体、纤维、界面摩擦及纤维断裂引起的阻尼，分析了湿度和温度对阻尼的影响，并揭示了正轴阻尼与纤维性能、基体性能和纤维体积含量之间的关系，其偏轴由正轴阻尼经过变换得到。

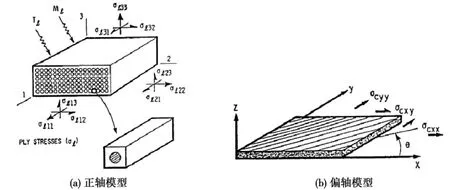
图3 Saravanos等的体积元模型

Finegan和Ioana设计了Cu丝增强树脂基复合材料的二维和三维有限元模型(图4)，利用了弹性理论、有限元方法、材料力学和应变能法分析了材料在轴向载荷、横向载荷、横向剪切载荷和轴向剪切载荷作用下的阻尼和刚度。

西安交通大学的张少辉等应用基于应变能的有限元方法研究了纤维增强复合材料的阻尼特性。此方法从单向复合材料的阻尼性能参数出发，通过有限元模态分析得到复合材料结构的模态损耗因子，与已有的理论分析和试验结果相比吻合较好，从而验证了该方法的合理性。该方法还可以比较三维应力分量对阻尼的贡献。

任勇生等建立了预测同时含有SMA层和SMA纤维混杂复合材料矩形板结构阻尼性能的数学模型，其中考虑了SMA纤维混杂复合材料矩形板夹芯的剪切变形，给出了上、下具有等厚度NiTi层，芯子为NiTi纤维混杂5层规则对称叠层(-θ/θ/-θ/θ/-θ)S的模态阻尼数值结构，分析了NiTi层厚度、NiTi层纤维含量、铺设角对阻尼性能的影响规律。

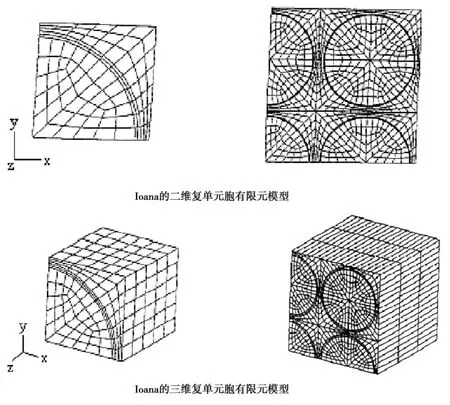
图4 Ioana的有限元模型

台湾国立交通大学的Tsai等对纤维复合材料的纤维排列方向对模态阻尼的影响进行了研究。阐述了单向复合材料三种不同纤维排列的微观结构，如矩形边缘填充(square edge packing，SEP)、矩形对角填充(square diagonal packing，SDP)和六角填充(hexagonal packing，HP)。广义单元法微观力学分析采用适合微观结构特征描述的重复单元。运用能量耗散概念计算复合材料主方向的具体阻尼能力。将微观力学分析得到的具体阻尼能力认定为复合材料的等效均匀阻尼性能。结合有限元分析的复合材料结构模型，复合材料杆和板的模态阻尼也能够反映其具体阻尼能力。分析中考虑了复合材料结构的无约束和单边约束状态。结果显示SDP纤维排列结构的阻尼行为要好于另外两种情况。

微观力学模型的建立不仅可以揭示复合材料宏观阻尼性能的内在机制，为复合材料及其结构阻尼性能分析提供理论依据和方法，而且能够对复合材料和结构进行微观层次上的设计，即根据实际需要选取适当的组分材料及优化的微观结构形式，设计出满足工程要求的阻尼复合材料。

6 提高阻尼的措施

纤维增强复合材料的阻尼是普通金属材料的10～100倍，但通常不超过1%，仍然无法满足工程应用的要求。因此需要通过一定的途径提高复合材料的阻尼性能。

提高和改善复合材料阻尼性能的方法有:(1)提高复合材料组分的阻尼性能;(2)将复合材料和高阻尼的粘弹性材料层粘合在一起(约束层阻尼处理、层间阻尼处理);(3)利用两种以上的纤维制成混杂复合材料。

Trego和Eastman提出一个复合材料阻尼的增强方案，在结构上采用了非对称纤维增强复合材料夹层结构，芯子为具有高阻尼性能的粘弹性层。Moser和Lumassegger在层合纤维/聚合物复合材料的轴向弯曲的应力零线位置埋入软质的叠层，利用其剪切变形产生附加阻尼。有限元分析结果表明，结构的基础模态损耗因子为0.3～0.5。

最近研究表明，共固化阻尼层的使用是提高复合材料结构的一种有效途径。张少辉等研究了共固化复合材料粘弹阻尼结构的损耗因子，同时考虑了粘弹性阻尼材料的频率依赖性和复合材料本身对振动能量的损耗，提出了该类型结构的有限元模型，并通过算例分析验证了该模型;考察了纤维增强复合材料本身的阻尼因素、柔性层的引入以及阻尼层的位置对复合材料粘弹阻尼结构损耗因子的影响，并给出了提高此类结构损耗因子的途径。

混杂铺层设计是较新的一个增加结构阻尼的方法，它在最大程度上减小了由于增加阻尼而导致复合材料的刚度和强度下降。Mantena等的研究表明，聚乙烯纤维增强铺层和石墨纤维增强铺层经过混杂铺叠后，得到了良好的阻尼和刚度性能。杨霜等为了使材料具有优异的力学性能，同时能对其阻尼性能进行设计，讨论了混杂纤维复合材料配方、铺层设计、外界温度、频率等对材料阻尼性能影响。

7 结论和展望

树脂基纤维复合材料属于多相混合各向异性材料，因此它的阻尼性能表现非常复杂。复合材料的阻尼性能同其弹性力学性能一样具有各向异性行为，也就是说在材料的不同方向上存在不同的阻尼性能。目前在材料层面，微观力学分析方法揭示了复合材料各组分在对形成各向异性阻尼性能所产生的作用，并且在一定的假设条件下，定量计算出各方向的阻尼系数。而在结构层面，宏观力学分析方法是通过测试得到的单向板各方向阻尼系数为基本计算单位，以各向异性复合材料力学分析为基础，建立能量损耗方程，最终得到层合板直至整个结构的阻尼性能。二者既统一又有很大区别，在复合材料结构阻尼分析过程中，从微观分析的角度可以在材料方面进行阻尼性能设计，从宏观分析的角度可以通过调整复合材料铺层的角度、顺序以及复合材料层合板截面的各种形式来进行阻尼性能的设计。尽管前人已经在该领域进行了大量的科学分析工作，但由于复合材料阻尼性能机理复杂，比如随着环境温湿度的变化，材料和结构的阻尼性能也发生改变。同时各个方向阻尼系数的测试方法和标准也没有完善和统一，国内外报道的测试结果有较大的差异。等等因素导致目前用来设计复合材料结构的阻尼性能的方法还未能够成熟应用，有待专家学者们继续深入研究。

［1］Schultz AB，Tsai SW.Dynamic moduli and damping ratio in fiberreinforced composites［J］.Composite Materials，1968(2):368 -379.

［2］Hashin Z.Complex moduli of viscoelastic composites:Ⅰ.General theory and application to particulate composites［J］.Solid and Structure，1970(6):539-552.

［3］Adams RD，Fox MAO，Flood RJ，et al.The dynamic properties of unidirectional carbon and glass fiber-reinforced plastics in torsion and flexure［J］.Comp Mater，1969(3):594-603.

［4］Adams RD，Bacon DGC.Measurement of flexural dynamic capacity and dynamic young′s modulus of metals and reinforced plastics［J］.Phys D:Appl Phys，1973(6):27-41.

［5］Adams RD，Bacon DGC.Effect of fiber orientation and laminate geometry on the dynamic properties of CFRP［J］.Compos Mater，1973(7):402-428.

［6］Ni RG，Adams RD.The damping and dynamic moduli of symmetric laminated composite beams:Theoretical and experimental results［J］.Compos Sci Technol，1984(18):104-121.

［7］Lin DX，Ni R，Adams RD.Prediction and measurement of the vibrational parameters of carbon and glass-fiber reinforced plastic plates［J］.Compos Mater，1984(18):132-152.

［8］Maheri MR，Adams RD.Finite element prediction of modal response of damped layered composite panels［J］.Compos Sci Technol，1995(55):13-23.

［9］Saravanos DA，Pereira JM.Effects of interply damping layers on the dynamic characteristics of composite plates［J］.AIAA，1992，30(12):2906-2913.

［10］Cupial P，Niziol J.Vibration and damping analysis of a three-layered composite plate with a viscoelastic mid-layer［J］.Sound Vib，1995，183(1):99-114.

［11］Berthelot JM，Sefrani Y.Damping analysis of unidirectional glass and Kevlar fiber composites［J］.Compos Sci Technol，2004 (64):1261-1278.

［12］Liao FS，Su AC，Hsu TC.Vibration damping of interleaved carbon fiber-epoxy composite beams［J］.Compos Mater，1994，28(8): 1840-1854.

［13］Yim JH.A damping analysis of composite laminates using the closed form expression for the basic damping of Poisson’s ratio［J］.Compos Struct，1999(46):405-411.

［14］Yim JH，Jang BZ.An analytical method for prediction of the damping in symmetric balanced laminates composites［J］.Polym Compos，1999，20(2):192-199.

［15］Yim JH，Gillespie Jr JW.Damping characteristics of 0°and 90° AS4/3501-6 unidirectional laminates including the transverse shear effect［J］.Compos Struct，2000(50):217-225.

［16］Yihua C，Li M，Su Y，et al.Studies on damping characteristics and parameter optimization of anisotropic laminated damped structure［J］.Aircr Eng Aerosp Technol，2002，74(4):332-327.

［17］Berthelot JM.Damping analysis of laminated beams and plates using the Ritz method［J］.Compos Struct，2006(74):186-201.

［18］Suzuki K，Kazuro K，Isao K，et al.Vibration and damping prediction of laminates with constrained viscoelastic layers-numerical analysis by a multilayer higher-order-deformable finite element and experimental observations［J］.Mech Adv Mater Struct，2003，10(1):43-75.

［19］Finegan IC，Ioana C，Gibson RF，et a1.Analytical modeling of dampingatmicromechanicallevelinpolmyercomopsites reinforced with coating fibers［J］.Comp Sci and Tech，2000，60 (7):1077-1084.

［20］Hajime K，Manabu K，Satoshi M，et a1.Damping properties of thermo plastic-elastomer interleaved carbon fiber-reinforced epoxy composites［J］.Comp Sci and Tech，2004(64):2517 -2526.

［21］Fujimoto J，Tamura T.Optical coherence tomography of glass reinforced polymer composites［J］.Comp Mater，1999(4):365 -371.

［22］Meunier M，Shenoi RA.Dynamic analysis of composite plates with damping modelled using high-order shear deformation theory［J］.Compos Struct，2001(54):243-254.

［23］Plagianakos TS，Saravanos DA.High-order layerwise mechanics and finite element for the damped dynamic characteristics of sandwich composite beams［J］.Solids Struct，2004(41):6853 -6871.

［24］Assarar M，El Mahi A，Berthelot J M.Damping analysis of sandwich materials［J］.Compos Mater，submitted for publication.

［25］廖英强，杜楠.复合材料的阻尼分析［J］.玻璃纤维，2007(1): 15-18.

［26］秦东奇，王静嫒.PU/PMMA IPN的阻尼行为研究［J］.高分子材料科学与工程，2000，16(5):95-98.

［27］钱军民，李旭祥.聚合物-无机纤维复合泡沫材料吸声性能的研究［J］.高分子材料科学与工程，2001，17(4):145-148.

［28］晏雄，张慧萍，住田雅夫.新型减振高分子复合材料研究［J］.高分子材料科学与工程，2001，17(5):86-89.

［29］李明俊，刘桂武.粘接层对各向异性层合阻尼结构内耗特性的影响［J］.复合材料学报，2005，22(4):96-95.

［30］孙大刚，诸文农.阻尼减振结构的动态优化［J］.工程机械，1997，28(11):22-25.

［31］杨雪，王源升.多层阻尼复合结构阻尼性能［J］.复合材料学报，2005，22(3):175-181.

［32］戴德沛.阻尼减振降噪技术［M］.西安:西安交通大学出版社，1986:62-80.

［33］胡卫强，王敏庆，刘志宏.悬臂梁弯曲共振法自由阻尼结构试件设计研究［J］.实验力学，2008，23(3):241-247.

［34］Chanadra R，Singh SP，Gupta K.Damping studies in fiber-reinforced composites-a review［J］.Composite Structures，1999 (46):41-51.

The Research Progress of Damping Property of Fiber Reinforced Resin Matrix Composite Materials

LIU Tao
(Liaoning ProvinceQuality Supervision and Test Institute，Shenyang 110144)

The damping property of resin matrix composite materials has anisotropic characteristic，which is similar to that of mechanical behavior.The structures and products，which have certain requirement on their damping behavior，have to be designed and analyzed according to some special procedures.In this study，the analytical procedures for the damping property of resin matrix composite materials were briefly described and concluded.The definition，classification and mechanical analysis on both microcosmic and macroscopic aspects were all covered in the study as well as the main research achievements of international and domestic specialists in this field，which provided a help reference for the design of damping property of composite structures and related products.

resin matrix composite material;damping;micromechanics;macromechanics

2016-05-11)

刘涛(1971-)，男，辽宁人，本科，助理工程师。研究方向:复合材料质量检测。

E-mail:13940295601@163.com.