移动中继协助下终端直通中的模式选择和资源分配方案

朱正仓,赵季红,唐睿,曲桦,王璐瑶,曹照鑫

(西安交通大学电子与信息工程学院,710049,西安)



移动中继协助下终端直通中的模式选择和资源分配方案

朱正仓,赵季红,唐睿,曲桦,王璐瑶,曹照鑫

(西安交通大学电子与信息工程学院,710049,西安)

针对移动中继(MR)协助下终端直通(D2D)链路与传统蜂窝链路之间的同频干扰问题,在MR是、否可被多条D2D链路复用的条件下,分别提出了2种联合模式选择和资源分配减小系统干扰的方案。在MR可被多条D2D链路复用的方案(方案1)中,通过干扰模型构建的优化问题等价于二分图中的最大匹配问题,继而可以借助匈牙利算法在多项式时间内得到最优解;在MR不可被多条D2D链路复用方案(方案2)中,通过干扰模型构建的优化问题等价于三维匹配问题,一般意义下属于NP-hard难题,因此设计了一种具有多项式复杂度的方案。仿真结果表明,方案1可得到理论最优解,其D2D链路总中断概率比贪婪方案降低了29.94%;方案2的D2D链路总中断概率比贪婪方案降低了23.67%,相比于最优值,仅仅损失了8.16%的性能,有效地实现了性能与复杂度之间的折中。

终端直通;移动中继;模式选择;资源分配

终端直通(device-to-device,D2D)通信容许邻近通信对间直接建立数据链路[1-2],无需基站转发数据,减轻了基站负担,降低了时延,已成为未来5G网络的重大课题[3]。然而,5G采用频谱已上升至30～300 GHz,无线信号绕过障碍物和穿透建筑物的能力变弱,致使远距离路径损耗严重,导致5G网络下D2D通信的可靠通信距离变短[4],同时,为提升小区频谱利用率,D2D用户复用已有蜂窝用户的频带资源,会产生严重的同频干扰问题。针对D2D用户的远距离可靠通信问题,文献[5]采用固定中继,以增强D2D链路间的信号质量,但固定中继需安装中继设备,增大了设备的投入费用;文献[6-7]将空闲的移动设备作为中继,即移动中继(mobile relays,MR),相比于固定中继,移动中继的选择增益和频谱复用增益能更有效地提升D2D链路的通信质量。基于此,本文借助移动中继协助D2D通信。

针对D2D链路用户复用蜂窝用户资源时会产生同频干扰的问题[8],如何设计有效的模式选择和无线资源分配方案以减小系统干扰引起了国内外学者的广泛探讨[5-7,9-14]。文献[5-6]借助资源分配降低D2D用户和蜂窝用户间干扰,分别优化系统吞吐量和能耗,但此系统只存在单一的中继模式,忽略了D2D通信的直通模式。考虑到文献[5-6]的不足,文献[7]通过联合模式选择和中继选择优化系统吞吐量,但未考虑信道资源分配,忽略了中继和信道的多维无线资源的联合优化。为此,文献[9-14]联合优化多维无线资源,但难以同时兼顾高算法性能和低算法时间复杂度的要求。首先,从算法性能上看,文献[9-10]借助贪婪算法求解问题,算法复杂度低,但算法性能难以保证;文献[11]通过启发式算法求解问题,无法保证最优解;文献[12]将目标问题的三维变量分别固定其中二维变量后利用匈牙利算法不断迭代求解,但易陷入局部最优,算法性能无法保证。其次,从算法时间复杂度上看,文献[13]以提升的穷举搜索方式求最优解,但算法时间复杂度高;文献[14]将四维优化问题固定其中三维变量转化为二维优化问题求最优解,但以遍历方式固定三维变量,算法复杂度高。

综上,针对MR是否可被多条D2D链路复用的不同场景,本文联合模式选择和资源分配分别提出2种减小系统干扰的方案。在中继可被复用场景中,该方案将构建的干扰模型公式化为四维优化问题,并将其转化为图论中的二维匹配问题,该二维优化问题可借助匈牙利算法求解,从而提出性能最优的方案1;在中继不可被复用场景中,该方案将构建的干扰模型同样公式化为四维优化问题,其可转化为三维优化问题,以此提出解决方案2,且方案2的性能接近最优的遍历方案。

1 系统模型

本文考虑单小区场景,假定小区间同频干扰已得到很好的抑制[1]。系统干扰模型如图1所示,小区内包含一个宏基站(macro base station,MBS),N个蜂窝用户(CN),M个D2D通信对(包括一个发送端DT和一个接收端DR)和L个空闲的移动中继用户(R),其中,移动中继采用放大发送(amplify-and-forward,AF)中继方式。本文考虑D2D通信复用蜂窝通信上行频带资源的情况,且蜂窝通信处于满负荷,即信道数为N。将蜂窝用户与MBS之间的链路称为蜂窝链路(cellular link,CL)。将DT和DR间的链路(包括直通模式下的单条链路和移动中继协助模式下的2跳链路)称为D2D链路(D2D link,DL)。

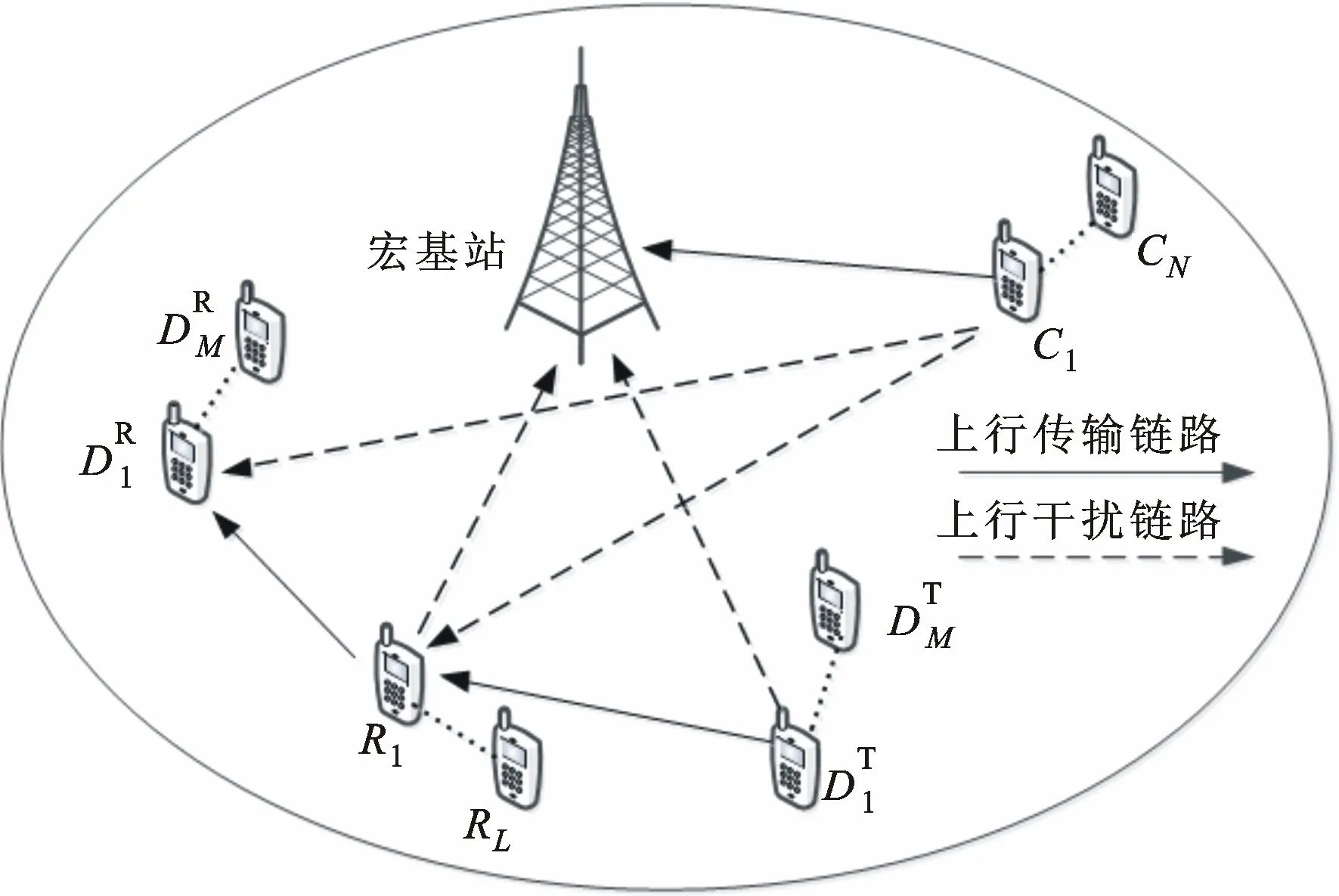
图1 系统干扰模型

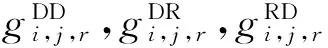
(1)

(2)

(3)

(4)

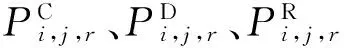
(5)

(6)

(7)

2 问题构建和解决方案

为减小D2D用户和MR用户复用蜂窝用户资源产生的干扰问题,联合模式选择和资源分配降低系统干扰,减小D2D链路总中断概率,提升D2D链路的可靠性,其优化过程分2个部分:首先,分析任意D2D链路在不同模式下的中断概率;其次,设计模式选择和资源分配方案。

2.1 D2D链路的中断概率

本文分别考虑D2D通信的直通和中继2种通信模式,需分析2种模式下D2D链路中断概率公式,以构建问题模型,见定理1。

定理1 直通模式下,D2D链路的中断概率为

(8)

中继模式下,D2D链路的中断概率为

(9)

证明 可详见附录A。

2.2 联合模式选择和资源分配

中继模式下,根据用户偏好,用户可设定中继是、否可被复用的2种场景。

2.2.1 中继可复用 本文联合模式选择和资源分配优化系统干扰,最小化D2D链路的总中断概率,其中,资源分配包括信道分配和中继选择,可将其干扰模型公式化为式(10)的优化问题(问题1)

(10)

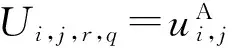
问题1(式(10))为四维优化问题,若直接求解则其算法复杂度高,可简化问题1,见定理2。

定理2 中继可复用时,问题1等价于二分图的最大匹配问题。

证明 在问题1中,可将直通模式的D2D接收端看作特殊的中继,即将模式选择与中继选择合并,其原理如图2所示,若D2D对在任意信道下选定中继节点L+1,则表示D2D对用户选择直通模式通信,否则,选择中继模式通信。

图2 中继可复用时模式选择与中继选择合并示意图

例如图2中,D2D对1选择信道2和中继L+1以直通模式通信,D2D对3选择信道1和中继2以中继模式通信,因此,问题1可转化为如下的三维优化问题(问题2)

(11)

式(11)的目标函数中:二元变量yi,j,r∈{0,1},yi,j,r=1表示D2D对j通过中继r以信道i通信,否则yi,j,r=0;当1≤r≤L时,Wi,j,r=Ui,j,r,1,当r=L+1时,Wi,j,r=Ui,j,r,2;目标函数的2个限制条件类似问题1中的限制条件,同样表示单个信道只能被单个D2D对和MR复用及单个D2D对只能使用单个信道和中继。

问题2(式(11))将问题1降为三维优化问题,根据中继可被复用条件与问题2的2个限制条件可进一步将问题2转化为二维优化问题,其过程如下式所示

(12)

式中:Mi,j=min{Wi,j,1,Wi,j,2,…,Wi,j,L+1},∀i,j;二元变量zi,j∈{0,1},其中zi,j=1表示D2D链路j通过中继r*在信道i通信,否则zi,j=0;步骤(a)的物理意义在于:在任意确定的信道i和D2D对j的情况下,选择D2D对j复用信道i时,使D2D链路中断概率最小的中继r*。根据式(12)可将问题2进一步转化为如下的问题(问题3)

(13)

综上,问题1可转化为问题3(式(13)),问题3易证明其等价于二分图的最大匹配问题[14],此处从略。因此,为求解问题3,可构建图论问题模型,借助匈牙利算法求解问题3中(i,j)间的最优匹配值zi,j,并可将二维优化变量zi,j还原为问题1的4维优化变量xi,j,r,q,证明结束。

本文根据定理2设计性能最优的方案1,其算法复杂度为O(J3+MN(L+1)),J=max(M,N)。方案1的详细步骤如下:

步骤1 设定M,N,L值,初始化矩阵W=[Wi,j,r]N×M×(L+1);

步骤2 构建二分图G=(V∪S,E),其中,集合V={j|1≤j≤M}表示D2D对的集合,集合S={i|1≤i≤N}表示可复用信道的集合,E为集合V与S中元素j和i的连接边,边的权值为Mi,j;

步骤3 借助匈牙利算法求解矩阵M=[Mi,j]N×M的二维最优匹配矩阵Z=[zi,j]N×M;

步骤4 ∀i,j,当zi,j=1时,搜索Mi,j=Wi,j,r的任一r*,若1≤r*≤L,则q=1且xi,j,r,q=1,若r*=L+1,则q=2且xi,j,r,q=1,否则xi,j,r,q=0,确定问题1的最优解xi,j,r,q。

2.2.2 中继不可复用 中继不可复用时,类似于构建式(10)的问题1,根据干扰模型,将其公式化为式(14)的优化问题(问题4)

(14)

问题4(式(14))类似于问题1,因为中继不可复用,问题4比问题1增加了一个限制条件(问题4的第3个限制条件),表示单个中继只能复用单个信道并协助单个D2D链路通信。

问题4为四维优化问题,可转化为三维优化问题,具体见定理3。

定理3 中继不可复用时,四维优化问题4等价于式(15)表示的三维优化问题5。

证明 在问题4中,合并模式选择与中继选择时,因中继不可复用,中继的维度需增加至L+M,以确保所有D2D对的直通模式可被选择,其示例过程如图3所示,L+1到L+M代表D2D用户以直通模式通信,图中D2D对2选择信道3以直通模式通信,因此问题4等价于式(15)的优化问题(问题5)

(15)

式中:1≤r≤L时,Ki,j,r=Ui,j,r,1;L+1≤r≤L+M时,Ki,j,r=Ui,j,r,2。证明结束。

图3 中继不可复用时模式选择与中继选择合并示意图

中继不可复用时,优化问题5(式(15))不满足式(8)中步骤(a)的转化条件,而且问题5为NP-难问题[14],算法设计的挑战在于找到一个逼近最优值的低复杂度算法。因此基于方案1,本文提出方案2,其复杂度为O(tJ3+MN(L+M))(t为被复用的中继个数,1≤t≤J)。

方案2的思路如下:首先设定包含(i,j,r)这3类元素的集合F,F表示所有未匹配的信道i,D2D对j和中继r;其次,先忽略问题5中的第3个限制条件,此时问题5等价于问题3,可借助方案1求出问题5的最优解,根据最优解重新考虑问题5中的第3个限制条件,其中,先筛选出最优解中被复用的中继集合,搜索中继集合中对应最小中断概率的D2D对和信道,将此D2D对,中继和对应信道记录并从集合F中除去;最后,根据更新后的集合F,重新循环使用方案1,直至无中继被复用时终止。

根据方案2的思路,其详细步骤如下:

步骤1 初始化矩阵K=[Ki,j,r]N×M×(L+M),构建集合F={(i,j,r)|1≤i≤N,1≤j≤M,1≤r≤L+M},k=0,F表示未匹配的D2D对,中继和信道的集合;

步骤2 构建二分图G=(V∪S,E),其中,集合V={j|1≤j≤M-k,j∈F}表示未匹配的D2D对集合,集合S={i|1≤i≤N-k,i∈F}表示未复用的信道集合,E为集合V与S中j和i的边,其权值Oi,j=min{Ki,j,1,Ki,j,2,…,Ki,j,L+M},∀i,j;

步骤3 借助匈牙利算法求矩阵O=[Oi,j]N×M的二维最优匹配矩阵Z=[zi,j]N×M;

步骤4 对∀i,j∈F,当zi,j=1时,搜索Oi,j=Ki,j,r中Ki,j,r的全部r(r∈F),令ti,j,r=1,否则ti,j,r=0,继而确定三维矩阵T=[ti,j,r]N×M×(L+M)值;

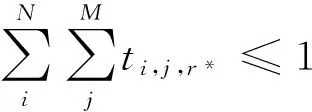
3 仿真结果与分析

假定仿真的蜂窝小区是半径为500 m的圆形小区,设定N=10,M=4,L=8,用户的最大发射功率Pmax=126 mW,基站和用户接收端的噪声分别为5 dB和9 dB,信道带宽为180 kHz,用户接收端的高斯噪声功率谱密度10-17.4mW/Hz,信道衰落服从瑞利衰落,且信道间相互独立同分布,信道的路径衰落常数β=102,路径损失系数α=4。

仿真设定的参考算法:①无中继方案[1],即D2D对间以直通模式通信,不考虑中继模式;②贪婪方案[9-10],即以贪婪原则进行联合模式选择和资源分配减小系统干扰的方案;③最优方案1[14],即中继可复用时,联合模式选择和资源分配减小系统干扰的最优方案;④最优方案2[12],即中继不可复用时,联合模式选择和资源分配减小系统干扰的最优方案。

针对中继是否可被复用,仿真分为以下2部分。

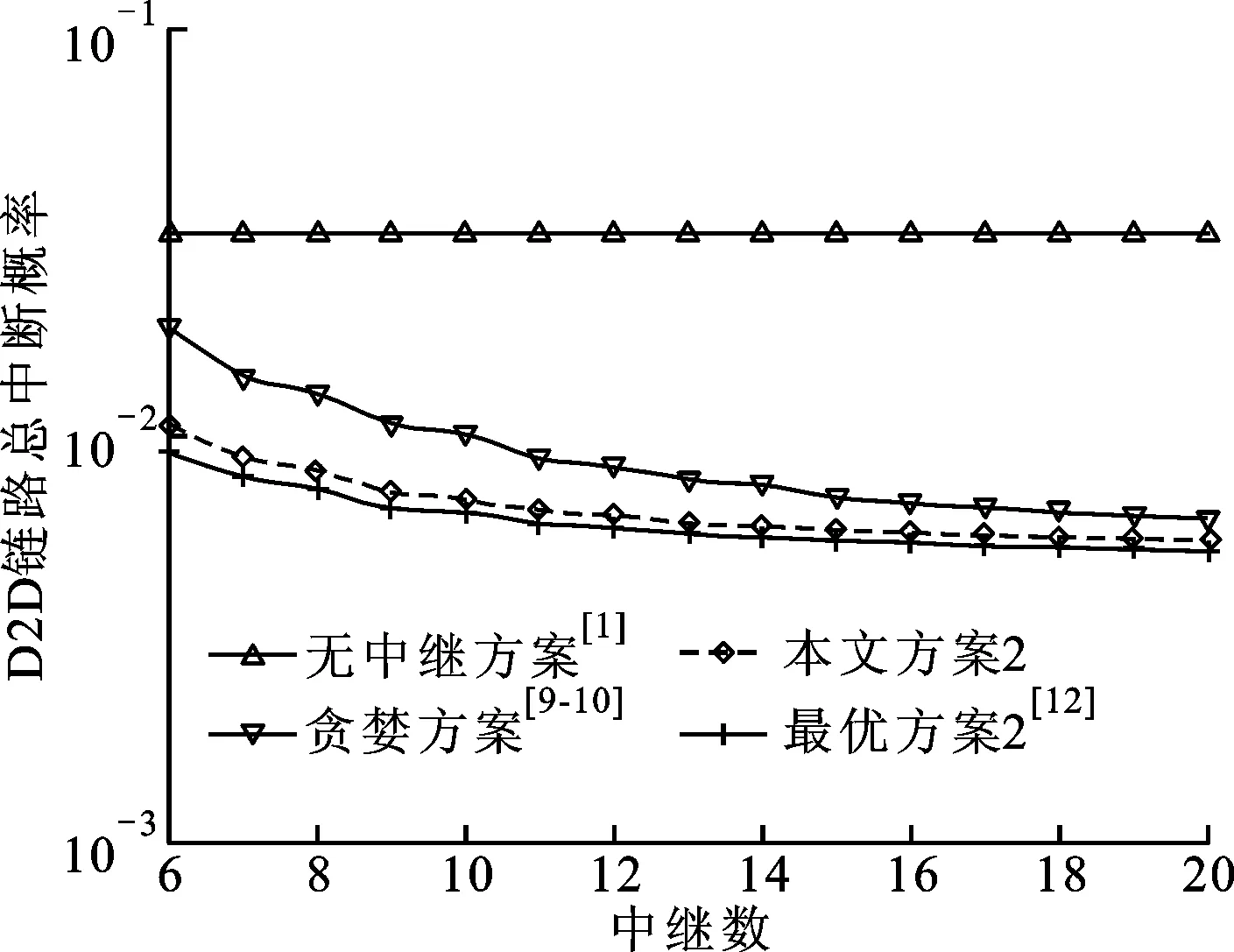
(1)在中继可被复用、中继数为6～20时,比较了本文方案1与3种参考方案的D2D链路总中断概率,结果如图4所示。由图4可见,本文方案1为联合优化的最优方案,性能优于文献[1]的直通模式方案和贪婪方案。其中,文献[1]方案中,中继不参与通信过程,故随着中继数目的增加其曲线不变,且本文方案1比其性能提升了72.23%。文献[14]方案与本文方案1同为最优方案,故2种方案曲线重合,但本文方案1的算法复杂度远低于文献[14]方案的算法复杂度(O(J3+MN(L+1))

图4 中继可复用时总中断概率与中继数的关系

图5 中继不可复用时总中断概率与中继数的关系

(2)在中继不可被复用、中继数为6～20时,比较本文方案2与3种参考方案的D2D链路总中断概率,结果如图5所示。由图5可见,本文方案2的性能优于文献[1]的直通模式方案和贪婪方案,而单纯考虑直通模式的文献[1]方案与中继无关,其曲线同样不会随着中继数变化,但考虑中继的本文方案2比文献[1]方案的性能提升了78.34%。本文方案2的性能接近文献[12]的最优方案,仅损失了8.16%,但本文方案2的时间复杂度O(t(J3+MN(L+M)))却远小于文献[12]的方案的时间复杂度O(J3HM,N),其中HM,N=max(M,N)!/[(max(M,N)-min(M,N))!]。

4 结 论

本文联合模式选择、资源分配以减小系统干扰,提升D2D链路性能,针对中继是否可被复用的场景分别提出本文方案1和本文方案2。本文方案1和文献[14]方案同为性能最优的方案,但本文方案1具有更低的时间复杂度(O(J3+MN(L+1))

[1] 杨阳, 廖学文, 高贞贞, 等. 多小区终端直通异构网络中利用图论的资源分配方案 [J]. 西安交通大学学报, 2014, 48(10): 22-28. YANG Yang, LIAO Xuewen, GAO Zhenzhen, et al. A resource allocation scheme using graph theory for D2D communication in multi-cell heterogeneous cellular network [J]. Journal of Xi’an Jiaotong University, 2014, 48(10): 22-28.

[2] 王元, 赵季红, 唐睿, 等. D2D多播场景下面向节能的资源分配机制 [J]. 西安电子科技大学学报, 2016, 43(2): 173-178. WANG Yuan, ZHAO Jihong, TANG Rui, et al. Energy aware resource allocation for underlaid D2D multicast [J]. Journal of Xidian University, 2016, 43(2): 173-178.

[3] YILMAZ O N C, LI Zexian, VALKEALAHTI K, et al. Smart mobility management for D2D communications in 5G networks [C]∥Proceedings of 2014 IEEE Wireless Communications and Networking Conference Workshops. Piscataway, NJ, USA: IEEE, 2014: 219-223.

[4] QIAO Jian, SHEN Xuemin, MARK J, et al. Enabling device-to-device communications in millimeter-wave 5G cellular networks [J]. IEEE Communications Magazine, 2015, 53(1): 209-215.

[5] HASAN M, HOSSAIN E, KIM D I. Resource allocation under channel uncertainties for relay-aided Device-to-Device communication underlaying LTE-A cellular networks [J]. IEEE Transactions on Wireless Communication, 2014, 13(4): 2322-2338.

[6] MA Xiran, YIN Rui, YU Guanding, et al. A distributed relay selection method for relay assisted device-to-device communication system [C]∥Proceedings of IEEE International Symposium on Personal Indoor and Mobile Radio Communication. Piscataway, NJ, USA: IEEE, 2012: 1020-1024.

[7] CHITHRA R, ROBERT B, SARAT K P. Hungarian method based joint transmission mode and relay selection in device-to-device communication [C]∥Proceedings of 2015 8th IFIP Wireless and Mobile Networking Conference. Piscataway, NJ, USA: IEEE, 2015: 261-268.

[8] 孙黎, 徐洪斌. 协作式终端直通系统中星座旋转辅助的干扰避免策略 [J]. 西安交通大学学报, 2015, 49(12): 6-11. SUN Li, XU Hongbin. A scheme to avoid interference via constellation rotation for cooperative device to device systems [J]. Journal of Xi’an Jiaotong University, 2015, 49(12): 6-11.

[9] ZHAO W, WANG S. Resource sharing scheme for Device-to-Device communication underlaying cellular networks [J]. IEEE Transactions on Communication, 2015, 63(12): 4838-4848.

[10]LI G Q, LIU H. Resource allocation for OFDMA relay networks with fairness constraints [J]. IEEE Journal on Selected Areas in Communications, 2006, 24(11): 2061-2069.

[11]JIA Juncheng, ZHANG Jin, ZHANG Qian. Cooperative relay for cognitive radio networks [C]∥Proceedings of IEEE INFOCOM. Piscataway, NJ, USA: IEEE, 2009: 2304-2312.

[12]KIM T, DONG Miaomiao. An iterative Hungarian method to joint relay selection and resource allocation for D2D communications [J]. IEEE Wireless Communications Letters, 2014, 3(6): 2162-2337.

[13]LU Zaixin, SHI Yan, WU Weili, et al. Efficient data retrieval scheduling for multi-channel wireless data broadcast [C]∥Proceedings of IEEE INFOCOM. Piscataway, NJ, USA: IEEE, 2012: 891-899.

[14]CHEN Hao, REN Pinyi, SUN Li, et al. A joint optimization of transmission mode selection and allocation for cognitive relay networks [C]∥Proceedings of IEEE International Conference on Communication. Piscataway, NJ, USA: IEEE, 2013: 2852-2856.

附录A

直通模式和中继模式D2D链路中断概率分析如下。

(1)直通模式:直通模式的D2D链路信干噪比为

(A1)

(A2)

Y的概率密度函数为

(A3)

令Z=X/Y,此时Z的概率密度函数为

(A4)

直通模式的D2D链路中断概率表达式为

(A5)

根据式(A4)、(A5)分析直通模式的D2D链路中断概率,可见正文式(8)。

(2)中继模式:根据式(7)推导中继模式D2D链路中断概率

(A8)

将式(A7)、(A8)代入式(A6),分析中继模式的D2D链路中断概率,见式(9)。

(编辑 刘杨)

Two Mode Selection and Resource Allocation Schedules for Device-to-Device Communication with Mobile Relay Assistance

ZHU Zhengcang,ZHAO Jihong,TANG Rui,QU Hua,WANG Luyao,CAO Zhaoxin

(School of Electronic and Information Engineering, Xi’an Jiaotong University, Xi’an 710049, China)

The joint allocation of transmission mode and resource is considered, and two mechanisms are proposed to address the problem of the severe mutual interference between mobile relay (MR) assisted device-to-device (D2D) communication and the existing cellular communication whether each MR can be reused by multiple D2D links. The problem model of interference is reduced into a bipartite matching problem in mechanism 1 when each MR can be reused by multiple D2D links, and the optimal solution of the problem is obtained in polynomial-time by using Hungary algorithm. The problem model of interference turns out to be a three-dimensional matching problem in mechanism 2 when each MR cannot be reused by multiple D2D links. The problem generally is NP-hard, and a heuristic algorithm is proposed to get its approximate optimum in polynomial-time. The results show that the proposed mechanism 1 maintains the optimal performance and outweighs the greedy scheme by 29.94%, and mechanism 2 achieves a 23.67% gain compared with the greedy scheme, and that a comparison with the optimal algorithm shows the proposed schemes attain polynomial-time complexity with only 8.16% performance loss.

device-to-device communication; mobile relay; mode selection; resource allocation

2016-03-07。

朱正仓(1987—),男,硕士生;赵季红(通信作者),女,教授,博士生导师。

国家自然科学基金资助项目(61372092);国家高技术研究发展计划资助项目(2014AA01A706)。

时间:2016-07-21

http:∥www.cnki.net/kcms/detail/61.1069.T.20160721.2212.008.html

10.7652/xjtuxb201610017

TN914.3

A

0253-987X(2016)10-0111-07