叠层式介电功能梯度绝缘子的介电常数分布优化
李文栋,刘哲,有晓宇,李晓冉,张冠军,董勤晓
(1.西安交通大学电力设备电气绝缘国家重点实验室,710049,西安;2.中国电力科学研究院,100192,北京)
叠层式介电功能梯度绝缘子的介电常数分布优化
李文栋1,刘哲1,有晓宇1,李晓冉1,张冠军1,董勤晓2
(1.西安交通大学电力设备电气绝缘国家重点实验室,710049,西安;2.中国电力科学研究院,100192,北京)
针对目前缺少介电功能梯度材料(d-FGM)内部介电特性分布的优化方法这一问题,提出了一种适用于交变电压下的叠层式介电常数FGM(ε-FGM)绝缘子内部介电特性的优化算法。该算法以降低绝缘子沿面最大电场强度为目标,使用迭代方法,根据当前电场强度、目标电场强度及介电常数上下限等设计参数,自适应地调整每层材料的介电常数,获得优化的介电常数分布;通过改变迭代系数和缩减系数,控制算法收敛过程,降低计算时间和资源消耗。仿真结果表明:相对于匀质绝缘子,ε-FGM绝缘子内部及沿面附近电场的不均匀程度得到明显改善,沿面最大场强的降幅超过60%;绝缘子的单层厚度应当在工艺条件满足的基础上尽可能地减小;沿面最大场强会随着介电常数上限的增加而非线性降低,存在饱和现象,饱和阈值与优化前的沿面最大场强呈正相关。研究结果验证了该算法的有效性,且表明以ε-FGM为代表的d-FGM具有优异的电场分布优化效果,有望在各类高压设备的固体绝缘系统中获得广泛的应用。
固体绝缘;功能梯度材料;电场分布
近年来,随着电力系统超/特高压、大容量输电的发展需求,以及脉冲功率、激光、微波等高新技术装备向高电压、小型化、高可靠性的方向发展,电气绝缘问题日趋突出。国内气体绝缘开关设备(GIS)各类闪络击穿事故频发,严重危害电力系统的安全稳定运行[1-2],如图1a所示。一些脉冲功率设备(如速调管、加速器、Z箍缩装置等)都曾发生过真空中绝缘子击穿引起的事故[3-5],如图1b所示。高电压、强电场下固体绝缘沿面上的放电破坏现象已成为制约电力设备和脉冲功率装备整体性能的关键问题。

(a)GIS盆式绝缘子 (b)脉冲功率圆台绝缘子图1 在沿面放电事故中损坏的高电压设备绝缘子
一般认为,电场不均匀度较高是实际绝缘设备因放电被破坏的重要原因。长期以来,为改善绝缘结构的电场分布,在材料类型固定的前提下,进行了很多优化电极和绝缘结构的工作,即控形(控制形状),常用方法包括增大电极曲率半径、增加屏蔽环等[6-9]。控形的方法起到了一定的作用,然而使绝缘结构更加复杂,增加了设备制造和维护的难度,调控效果也较为有限[10]。
通过调整材料的内在属性来改善电场分布,即控性(控制性质)。材料学领域中功能梯度材料(FGM)的概念就属于控性的范畴,其特征为材料特性在内部不同空间位置上呈现梯度变化,被广泛的应用于航空航天、生物工程、机械工程等领域[11-13]。类似的,通过调控材料内部的介电特性(如介电常数ε、电导率γ等)的分布,完全可以有效调控绝缘结构的电场分布,且相对于传统的控形方法,FGM这类控性方法具有绝缘结构简单、调控方式灵活等明显的优势。
国内外对介电功能梯度材料(d-FGM)绝缘子开展了初步的研究工作。文献[14-16]基于离心制造技术,制备了d-FGM绝缘子,SF6气体氛围下的实验表明:绝缘子的雷电冲击闪络电压相对于匀质绝缘子提高约10%~50%。文献[17]对给定介电常数分布的d-FGM绝缘子进行了几何形状优化的研究。文献[18]通过计算机仿真,认为d-FGM材料能够将原本不均匀的电场均匀化。文献[19-20]进行了叠层式d-FGM绝缘子的制备,表明相对于匀质绝缘子,其在真空下的雷电冲击闪络电压得到了一定的提升。
目前,作为一种新型的功能绝缘材料和结构的d-FGM绝缘子的研究仍然处于探索阶段,其中介电梯度分布优化设计需要将材料特性参数控制与电场优化结合考虑,增加了设计灵活性的同时也增加了其复杂性。前人的研究大部分是在介电参数分布已经确定的情况下进行电场计算,用来验证FGM优化电场的效果,较少进行介电参数分布优化的研究,对算法约束条件与优化效果之间的影响关系的研究也不多见。
本文以d-FGM中的介电常数FGM(ε-FGM)为研究对象,针对交流GIS及脉冲功率设备中3种典型的ε-FGM绝缘子模型(圆台、盘式及盆式)进行了介电常数分布的优化,并进一步分析了设计参数对优化效果的影响。沿面场强得到大幅降低,证明了本文优化方法的有效性。
1 d-FGM调控电场分布的机理
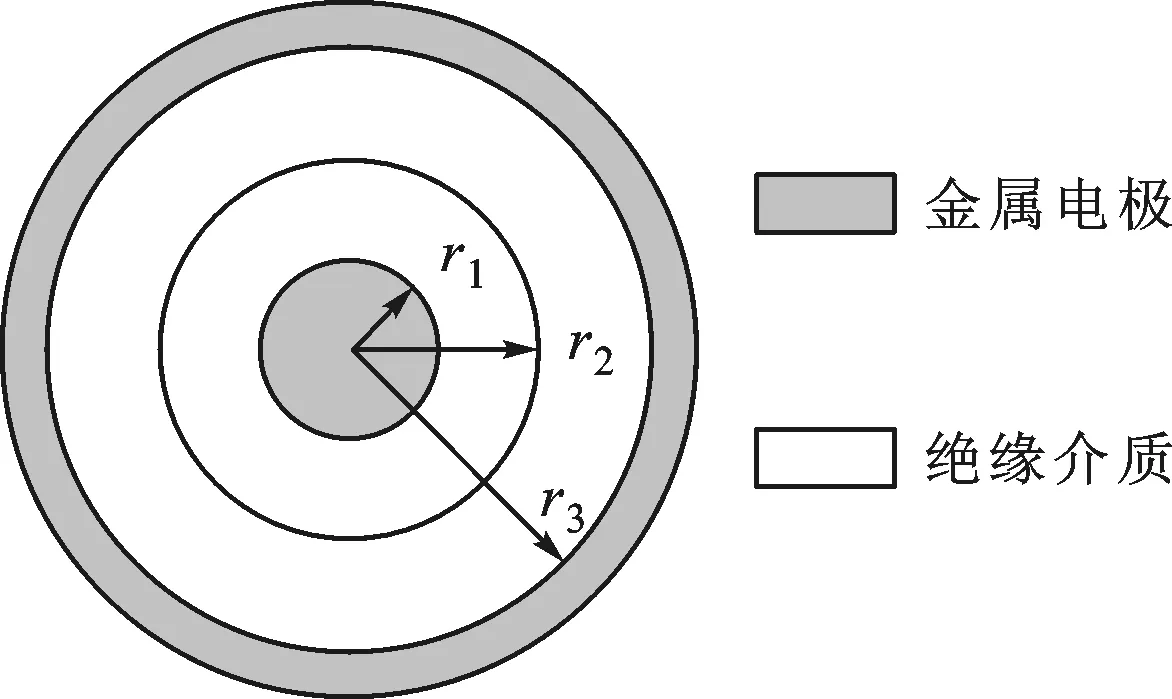
根据所调控的介电参数,d-FGM可以进一步分为介电常数FGM(ε-FGM)和电导率FGM(γ-FGM)两类,其中ε-FGM绝缘子调控电场分布可由高斯定理等推导得到。以图2a中的同轴圆柱形双层介质结构为例,在实际工频及雷电冲击电压下,介质电场可采用准静态近似,若进一步忽略电导的影响,则可将介质电场等效为静电场。此时,若双层介质的介电常数分别为ε1、ε2,则可以得到内、外层介质上的电压降分别为[21]
(1)
式中:U1、U2分别为内、外层介质上的电压降;U=U1+U2为内外电极之间的总电势差;r为介质中某点到轴线的距离;r1、r2、r3的定义如图2a所示。进一步考虑到各层中的最大场强E1max、E2max均在其内圆柱的外表面以及D=εE,可得
(2)
由式(2)可知,若双层介质的介电常数相等(ε1=ε2),则E1max/E2max=r2/r1,由于r2>r1,所以E1max>E2max,如图2b所示。若介质为不均匀介质且ε1>ε2,则E1max和E2max会比较接近,见图2c。
(a)结构示意图
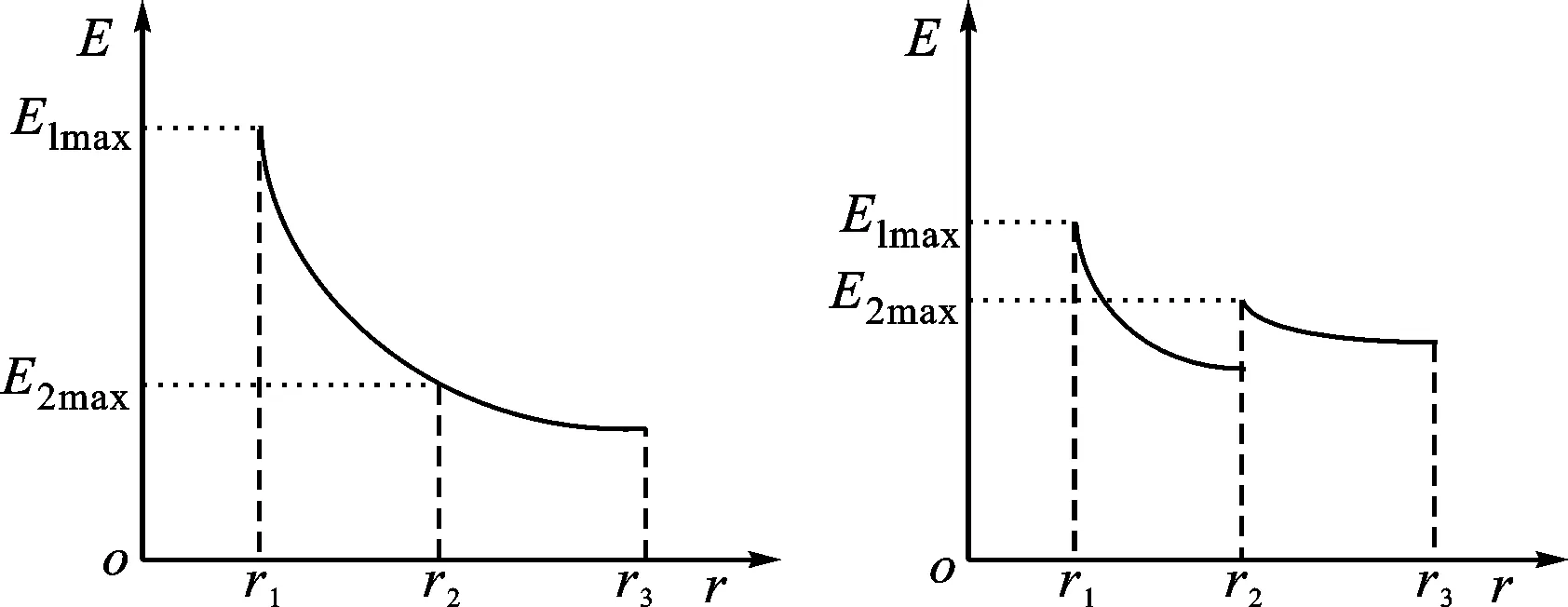
(b)ε1=ε2 (c)ε1>ε2图2 双层ε-FGM介质的结构及电场分布
类似地,用电导率γ代替介电常数ε,并利用分界面上的电流连续性,就可以针对双层γ-FGM得到类似的关系E1maxγ1r1=E2maxγ2r2。此时,若内层介质电导率γ1大于外层介质电导率γ2,则介质电场分布也将得到优化。
由上述的讨论可以看出,对于双层介质,通过提高局部电场集中区域材料的介电常数或电导率,均可以达到均匀电场的目的。类似的结论可扩展到层数n>2的多层介质以及介电常数连续分布的d-FGM介质。实际上,此类非均匀绝缘的设想已经在高压电力电缆和电机绕组槽口等场合有所应用,并使其电晕起始电压得到提升[21]。这进一步佐证了d-FGM介质在优化电场分布上的可能性。
众所周知,在交流和脉冲电压激励下的电场分布主要由介电常数ε决定,直流电压作用下的电场分布由γ决定(在交流及冲击电压下,流过绝缘材料的位移电流远大于传导电流,介电常数的影响较为明显,而在直流电压条件下,稳态仅有传导电流,电场分布则主要由电导率分布决定)。另一方面,相对于ε,γ受温度影响明显,导致可调控性差。因此,采用调控ε的方法来改善电场分布更为有效。本文亦将针对ε-FGM进行研究。
2 ε -FGM绝缘子介电常数分布优化
2.1 典型ε-FGM绝缘子模型
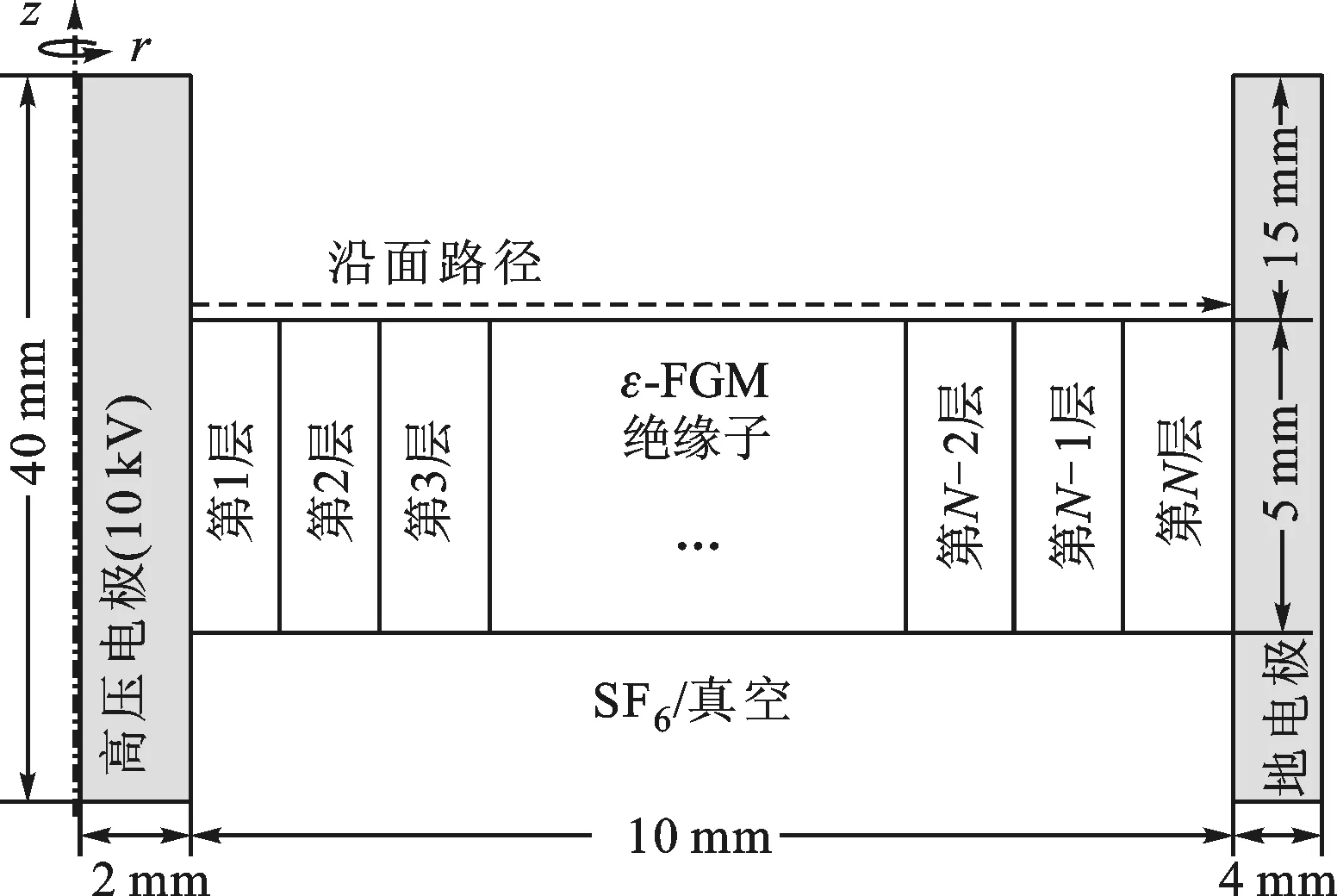
对交流GIS及脉冲功率设备中3种典型的绝缘子模型(圆台、盘式以及盆式)进行优化计算。3种模型均为轴对称结构,其中ε-FGM绝缘子置于高压电极与地电极之间,电压U为10 kV,电极间距d均为10 mm,圆台与盆式绝缘子中绝缘子与介质的夹角均为45°,与脉冲功率设备中的经验值一致[22]。整个模型置于气体或真空氛围中(介电常数均为1)。模型中的绝缘子被均匀切分成了N个叠层,每层薄片的介电常数均可以在一定范围内变化,以此构成一维叠层式ε-FGM绝缘子结构,如图3所示。
2.2 介电常数分布优化算法
本文使用迭代计算的方法进行介电常数分布的优化工作。待优化变量为叠层式ε-FGM绝缘子每层材料的介电常数(约束在一定范围内),优化目标为降低绝缘子沿面路径(见图3)的最大电场强度Emax。算法流程如图4所示,其中ε-FGM绝缘子各层的初始介电常数均设为4(接近常用的环氧树脂材料的介电常数),作为优化的初始条件。
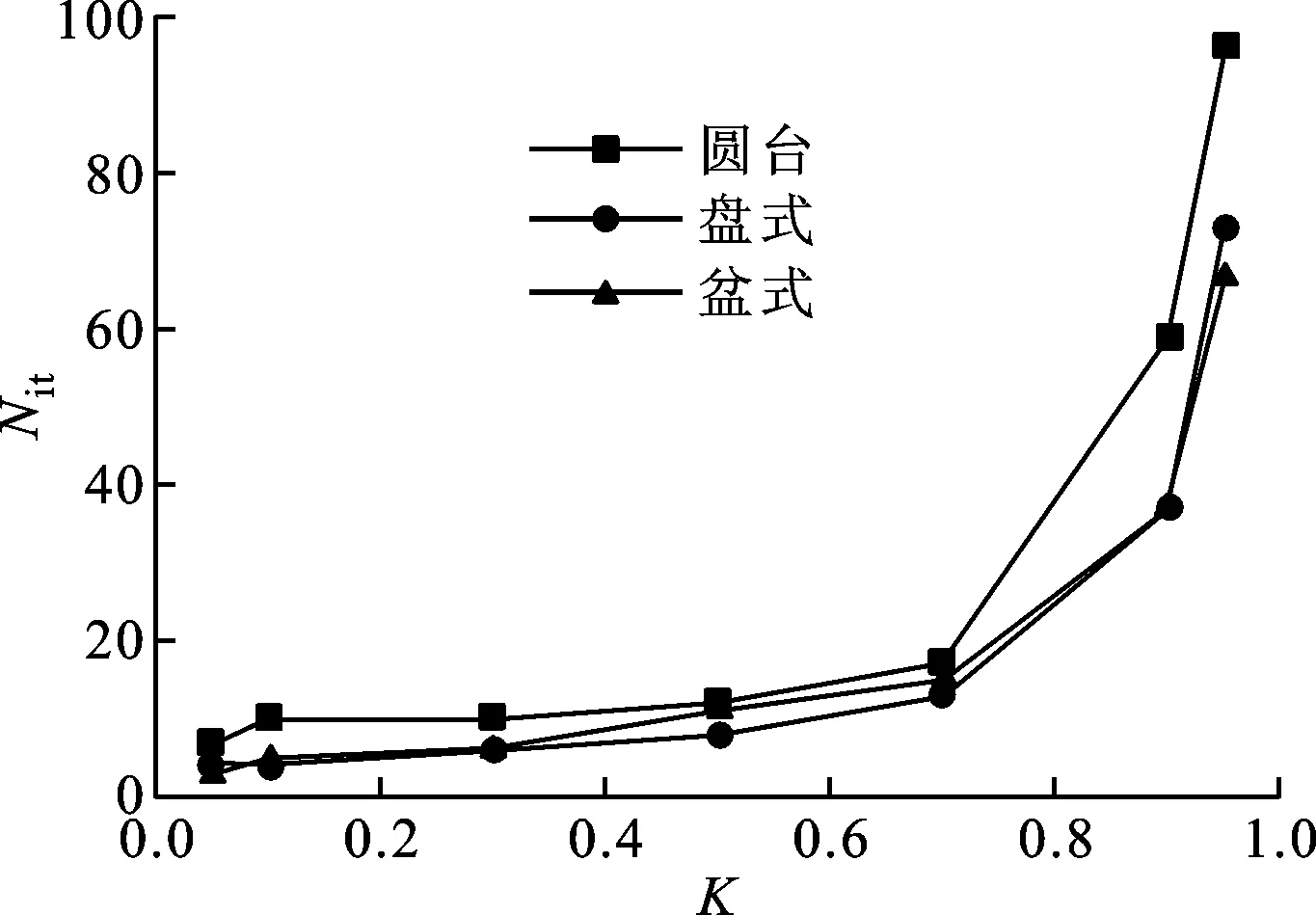
对于第i层(1 (3) (a)圆台绝缘子 (b)盘式绝缘子 (c)盆式绝缘子图3 叠层式FGM绝缘子模型结构 图4 介电常数优化算法流程 2.3 算法实现方式 本文优化方法是在MATLAB代码中调用有限元软件ANSYS实现,其中利用MATLAB进行总体的优化工作,利用ANSYS进行ε-FGM绝缘子电场分布的计算,ANSYS和MATLAB之间通过存储介电常数及电场强度分布的两个列表文件进行数据交换,总体流程如图5所示。 图5 优化算法软件实现 在优化过程中,首先确定优化计算所需的各项参数,如缩减系数K、叠层数目N、介电常数上下限εmax和εmin等。程序同时给出介电常数的初始分布,本文中各层材料的介电常数初值均为εmin。初始化完成之后,计算程序进行绝缘子模型介电常数分布的迭代优化,直到满足2.2节中的优化终止条件。优化结束后,MATLAB将优化结果(包含基本信息、介电常数优化值、电场强度计算值等)输出至Excel文件,供后续分析使用。 本文使用ANSYS v14.5进行电场数值计算。采用ANSYS参数化设计语言(APDL)编写运算脚本,以绝缘子的轴向截面作为计算对象。计算过程中采用静电场等效,选取二维静电场分析单元plane121作为单元类型。网格剖分采用用户控制的剖分方法,网格尺寸为0.05 mm,具有较高的解析度。后处理阶段通过APDL指令,实现交界面电场强度及其切向、法向电场分量的求取及导出,与MATLAB程序配合实现介电常数分布的优化求解。 3.1 缩减系数K对优化的影响 在本文研究过程中,发现缩减系数K对Emax及迭代次数Nit均有影响。为了研究K的影响,针对3种绝缘子模型进行了优化,优化过程中εmax和εmin分别取100和4,叠层数目N取100,K在0.05~0.95之间变化,结果如图6所示。 (a)Emax (b)迭代次数Nit图6 K对优化后的Emax及迭代次数的影响 从图6可以看出,当K小于0.3时,优化后Emax随K的增大而降低,在K超过0.3之后,对优化后Emax的影响减小,此时沿面最大场强接近系统平均值,优化效果较好。然而,随着K的进一步增大,特别是当K>0.7时,迭代次数Nit将会随着K的增大而迅速增加,在Emax并没有显著变化的情况下,Nit的增加意味着消耗更多的计算时间及资源,导致优化算法效率的降低。综上所述,K应在0.3~0.7之间进行选取,本文选取0.5作为后续优化计算中的缩减系数。 3.2 电场优化效果 本文对比了3种叠层式ε-FGM绝缘子优化前、后整体及沿面路径上的电场强度分布,如图7及图8所示,同时给出了优化后的ε-FGM绝缘子各层介电常数分布,如图9所示。在优化过程中,εmax、εmin及N取值与3.1节相同,K取0.5。 对比优化前后绝缘子内部及沿面的电场分布,可以看出,相比较于匀质绝缘子(ε均匀为4.0),ε-FGM绝缘子沿面Emax从(2.5~6)×104V/cm降低到了(1~1.5)×104V/cm,降低幅度超过60%,接近目标场强,绝缘子内部及沿面附近的电场不均匀度明显降低。这证明了本文优化方法的有效性,同时验证了ε-FGM绝缘子在电场调控上的显著潜力。 由图9可以看出,虽然优化算法设置的介电常数上限εmax是100,但是最终3种绝缘子模型优化得到的介电常数最大值均未达到εmax。与图7的对比表明,介电常数的分布与初始匀质材料的电场分布较为类似。 (a)圆台绝缘子 (b)盘式绝缘子 (c)盆式绝缘子图7 绝缘子沿面电场强度分布对比 3.3 叠层数对优化效果的影响 本节在前述优化方法的基础上,进一步研究了叠层数N对优化效果(Emax、Nit及电场均匀性)的影响,优化过程中εmax=100、εmin=4、K=0.5,研究结果如图10、图11及表1所示(1层对应匀质绝缘子)。从结果可以看出,对于3类典型绝缘子模型,叠层数目的增加(即叠层厚度的减小)均会使Emax降低。若叠层数过少,优化后的Emax仍然较大(见图10),层间界面上的电场集中现象较为明显(见图11);当N>10时,Emax的降低将趋于饱和,优化效果明显。由图11可以进一步看出,叠层数越大,叠层厚度越小,沿面电场分布的波动越小,分界面上的电场集中现象也将得到抑制。 (a)圆台绝缘子 (b)盘式绝缘子 (c)盆式绝缘子图8 优化前后绝缘子电场分布图 图9 ε-FGM绝缘子介电常数分布 因此,在叠层式ε-FGM绝缘子的制备过程中,叠层数应当在工艺条件满足的基础上尽可能的增加,即每层厚度应尽可能减薄。 由表1可知,迭代次数Nit的变化不明显,算法的运行时间和效率受到叠层数目的影响不明显。需要指出的是,当绝缘子层数为1时,不存在优化问题,因此迭代次数为1。在仿真过程中发现,圆台绝缘子在层数N=2时,优化计算无法收敛,而在盘式和盆式绝缘子模型中没有出现这一问题。这可能是由于在圆台式绝缘子模型中,高压电极处介质沿面与电极表面夹角小于90°,当介质介电常数大于真空介电常数时,沿面电极-介质-气体(真空氛围)三结合点处的电场将得到增强,且这一增强效应随着介质介电常数的增加而更加显著。因此,在优化过程中,若局部三结合点电场增强的效应无法被整体的电场平均效应给抵消,则沿面最大场强Emax将无法得到降低,最终导致算法发散及优化失效。 (a)5层 (b)10层 (c)20层 (d)100层图11 叠层数N对盘式绝缘子沿面电场分布的影响 NNit圆台盘式盆式1*1112983131011414101051210910129142011916401391760121016801391610012916 注:加“*”数据对应介电常数为4的匀质绝缘子。 经过进一步的计算与分析,作者初步认为,可能出现算法发散现象的条件有:①叠层数N较少;②初始电场不均匀度较低;③某一区域材料介电常数的增加会提升该区域的电场强度(增强效应)。在不改变绝缘子整体结构的情况下,增加叠层数N可以有效地避免这一问题的出现。 3.4 介电常数调整范围对优化效果的影响 针对层数为100的ε-FGM绝缘子模型,本文进一步研究了介电常数变化范围对优化效果的影响。令介电常数下限εmin固定为4,εmax在10~320范围内变化,研究εmax对优化效果的影响,结果如图12所示(εmax=4对应匀质绝缘子)。从图中可以看出,对于3类绝缘子模型,随着εmax的增加,沿面最大场强Emax逐渐减小,优化效果得到提升。不过,Emax减小的速率将随着εmax的增加而逐渐降低,下降过程呈现非线性下降并逐渐趋于饱和的特点。对于圆台和盘式绝缘子,Emax下降出现饱和的εmax阈值为60;对于盆式绝缘子,εmax饱和阈值约为200。 图12 介电常数上限对优化效果的影响 对于这一饱和现象,结合3.2节中的匀质绝缘子的沿面电场分布,可以初步认为,εmax的饱和阈值与待优化绝缘结构优化前的最大电场强度及电场不均匀度有关。由图8可知,对于本文的圆台及盘式绝缘子模型,优化前Emax均在(2.5~3.0)×103V/cm范围之内,且两者较为接近,而对于盆式绝缘子模型,其优化前Emax均在约为6×104V/cm,远高于另两类绝缘子模型的值。由此可以看出,对于本文中的绝缘子模型,εmax的饱和阈值与优化前最大电场强度Emax呈正相关,Emax越高,εmax的饱和阈值也越大。 本文依据电磁场理论,阐述了介电功能梯度绝缘材料通过改变材料内部介电特性(介电常数或电导率)来改善绝缘系统电场分布的机理。针对ε-FGM绝缘子,提出了一种绝缘子内部材料介电常数分布的迭代优化算法,引入了缩减系数K用于控制算法的运行速度,并给出了基于MATLAB+ANSYS的算法实现方式。针对圆台、盘式及盆式3种叠层式ε-FGM绝缘子结构,本文使用提出的优化方法,进行了电场优化效果及其影响因素的仿真研究。 (1)为了保证优化效果,减少迭代次数,缩减系数K应在0.3~0.7之间进行选取。 (2)电场优化结果表明,相对于传统的匀质绝缘子,ε-FGM绝缘子沿面最大场强Emax降幅超过60%,内部及沿面附近的电场不均匀度明显降低。 (3)叠层厚度影响的研究表明,对于叠层式ε-FGM绝缘子,单层厚度应当在工艺条件满足的基础上尽可能地减小。 (4)当单层材料的介电常数下限固定时,沿面最大场强会随着叠层最大介电常数的增加而非线性降低,在其超过一定阈值后趋于饱和,饱和阈值与优化前的沿面最大场强呈正相关。 上述结论证明了本文方法的有效性,同时验证了ε-FGM绝缘子均匀电场分布的能力。可以认为,基于其优异的电场分布优化效果,以ε-FGM为代表的d-FGM绝缘子有望在各类高压设备中获得广泛的应用。 [1] 禹化然, 蒋伟毅, 徐嵘. 一起220 kV GIS内部短路故障分析 [J]. 高压电器, 2013, 49(8): 115-118. YU Huaran, JIANG Weiyi, XU Rong. Analysis of a short circuit fault in a 220 kV gas insulated switchgear [J]. High Voltage Apparatus, 2013, 49(8): 115-118. [2] 汪晓明, 何萍, 刘衍, 等. 一起500 kV HGIS事故的分析及处理 [J]. 高压电器, 2014, 50(1): 129-132. WANG Xiaoming, HE Ping, LIU Yan, et al. Analysis and treatment of a 500 kV hybrid gas insulated switchgear accident [J]. High Voltage Apparatus, 2014, 50(1): 129-132. [3] SAITO Y, MICHIZONO S, ANAMI S, et al. Surface flashover on alumina RF windows for high-power use [J]. IEEE Transactions on Electrical Insulation, 1993, 28(4): 566-573. [4] CRAVEY W R, DEVLIN G L, MAYBERRY C S, et al. Investigation of a high voltage vacuum insulator for the DARHT accelerator [C]∥IEEE International Pulsed Power Conference. Piscataway, NJ, USA: IEEE, 1997: 555-558. [5] SHOUP R W, LONG F, MARTIN T H, et al. Design validation of the PBFA-Z vacuum insulator stack [C]∥IEEE International Pulsed Power Conference. Piscataway, NJ, USA: IEEE, 1997: 1608-1613. [6] STIH Z. High-voltage insulating system-design by application of electrode and insulator contour optimization [J]. IEEE Transactions on Electrical Insulation, 1986, 21(4): 579-584. [7] 孙西昌, 彭宗仁, 党镇平, 等. 特高压交流架空线路用复合绝缘子均压特性研究 [J]. 高压电器, 2008, 44(6): 527-530. SUN Xichang, PENG Zongren, DANG Zhenping, et al. Study on electrical stress grading of composite insulators for UHV transmission lines [J]. High Voltage Apparatus, 2008, 44(6): 527-530. [8] 马爱清, 杨秀, 陆鑫淼, 等. GIS盘式绝缘子三维电计算及其逆问题分析 [J]. 高电压技术, 2010, 36(5): 1217-1221. MA Aiqing, YANG Xiu, LU Xinmiao, et al. 3D electric field calculation and its inverse problem analysis of disk-type insulator in GIS [J]. High Voltage Engineering, 2010, 36(5): 1217-1221. [9] 司马文霞, 施健, 袁涛, 等. 特高压复合绝缘子电场计算及基于神经网络遗传算法的均压环结构优化设计 [J]. 高电压技术, 2012, 38(2): 257-265. SIMA Wenxia, SHI Jian, YUAN Tao, et al. Electric field calculation of ultra high voltage composite insulator and optimization design of corona ring structure based on neural network and genetic algorithm [J]. High Voltage Engineering, 2012, 38(2): 257-265. [10]何金良, 谢竟成, 胡军. 改善不均匀电场的非线性复合材料研究进展 [J]. 高电压技术, 2014, 40(3): 637-647. HE Jinliang, XIE Jingcheng, HU Jun. Progress of nonlinear polymer composites for improving nonuniform electrical fields [J]. High Voltage Engineering, 2014, 40(3): 637-647. [11]KOIZUMI M. FGM activities in Japan [J]. Composites: Part B Engineering, 1997, 28(1/2): 1-4. [12]李信, 刘海昌, 滕元成, 等. 功能梯度材料的研究现状及展望 [J]. 材料导报, 2012, 26(S1): 370-373. LI Xin, LIU Haichang, TENG Yuancheng, et al. Research status and future directions on functionally gradient materials [J]. Materials Review, 2012, 26(S1): 370-373. [13]温变英. 聚合物梯度材料的制备及材料结构与性能研究 [D]. 北京: 北京化工大学, 2003: 1-17. [14]KATO K, KURIMOTO M, SHUMIYA H, et al. Application of functionally graded material for solid insulator in gaseous insulation system [J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2006, 13(2): 362-372. [15]KURIMOTO M, KATO K, HANAI M, et al. Application of functionally graded material for reducing electric field on electrode and spacer interface [J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2010, 17(1): 256-263. [16]ISHIGURO J, KURIMOTO M, KOJIMA H, et al. Electric field control in coaxial disk-type solid insulator by functionally graded materials (FGM) [C]∥IEEE Conference on Electrical Insulation and Dielectric Phenomena (CEIDP). Piscataway, NJ, USA: IEEE, 2014: 663-666. [17]JU H J, KO K C, KIM D K. Optimization of a grounded electrode shape in gas insulated switchgear with a reversely elliptical permittivity graded insulator [J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2013, 20(5): 1749-1754. [18]陈维, 唐泽荣, 缪江平, 等. 过滤法制备介电梯度功能材料的介电特性的研究 [J]. 应用科学学报, 2001, 19(2): 178-181. CHEN Wei, TANG Zerong, MIAO Jiangping, et al. A study of dielectrical properties of functional gradient material manufactured by a filtration method [J]. Journal of Applied Sciences, 2001, 19(2): 178-181 [19]LI Shengtao, ZHANG Tuo, SUN Jian, et al. Improvement of surface flashover performance in vacuum by co-firing Mo/Al2O3cermets and Al2O3ceramics [J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2010, 17(6): 1931-1937. [20]HUANG Qifeng, LI Shengtao, ZHANG Tuo, et al. Improvement of surface flashover characteristics about 45° insulator configuration in vacuum by a new organic insulation structure [J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2011, 18(6): 2115-2122. [21]严璋, 朱德恒. 高电压绝缘技术 [M]. 北京: 中国电力出版社, 2007: 16-18. [22]MILLER H C. Flashover of insulators in vacuum: review of the phenomena and techniques to improved holdoff voltage [J]. IEEE Transactions on Electrical Insulation, 1993, 28(4): 512-527. [23]OKUBO H, SHUMIYA H, ITO M, et al. Optimization techniques on permittivity distribution in permittivity graded solid insulators [C]∥IEEE International Symposium on Electrical Insulation. Piscataway, NJ, USA: IEEE, 2006: 519-522. (编辑 杜秀杰) Permittivity Distribution Optimization for Multi-Layer Dielectric FGM Insulator LI Wendong1,LIU Zhe1,YOU Xiaoyu1,LI Xiaoran1,ZHANG Guanjun1,DONG Qinxiao2 (1. State Key Laboratory of Electrical Insulation and Power Equipment, Xi’an Jiaotong University, Xi’an 710049, China;2. China Electric Power Research Institute, Beijing 100192, China) At the present there lacks proper optimization method for internal dielectric properties of dielectric functionally-graded-material (d-FGM). An optimization algorithm of internal permittivity distribution for multi-layer permittivity FGM (ε-FGM) insulator under AC voltage is proposed, which aims at weakening the maximum electric field (e-field) strength along the insulator surface. According to design parameters, such as current e-field strength, objective e-field value and permittivity range, the permittivity value of each layer is self-adaptively updated with iterations to obtain the optimized permittivity distribution. The iterative coefficient and shrinking coefficient are adjusted to control the convergence process and shorten calculation period. Compared with uniform insulator, e-field distribution inside and along the surface ofε-FGM insulator is more uniform and the maximum e-field strength along surface is weakened more than 60%, and the layer thickness of the multi-layerε-FGM insulator ought to be set as small as possible under the allowed fabrication conditions. The maximum surface e-field strength decreases nonlinearly with the increasing permittivity upper limit and saturates as the upper limit reaches certain threshold value, which has positive correlation with the maximum e-field strength before optimization. solid insulation; functionally graded material; electric field distribution 2016-01-04。 李文栋(1989—),男,博士生;张冠军(通信作者),男,教授,博士生导师。 国家重点基础研究发展计划资助项目(2015CB251003);国家自然科学基金创新研究群体资助项目(51521065);国家杰出青年科学基金资助项目(51125029)。 时间:2016-07-14 http:∥www.cnki.net/kcms/detail/61.1069.T.20160714.1733.020.html 10.7652/xjtuxb201610004 TM854 A 0253-987X(2016)10-0019-08




3 结果及分析


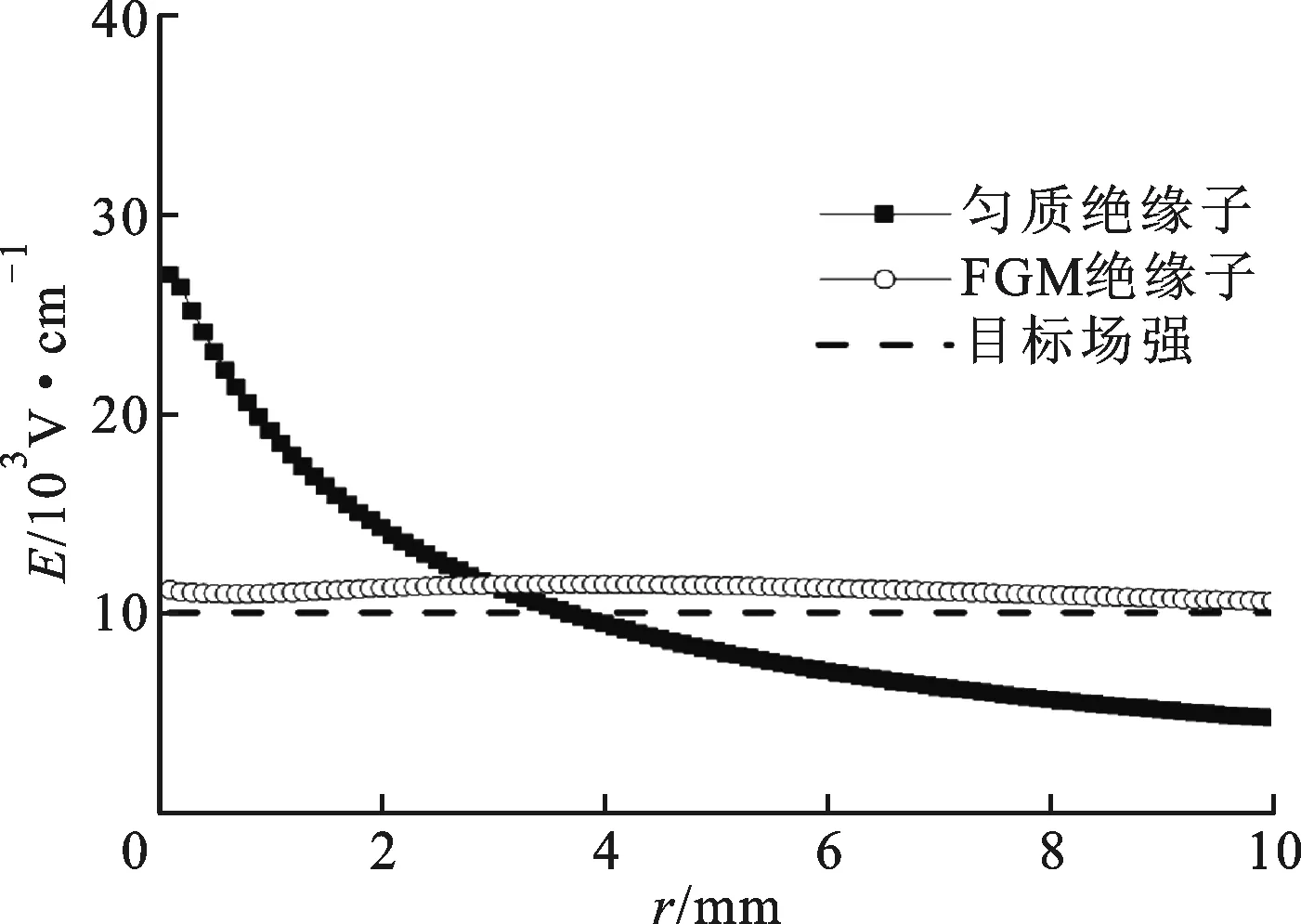
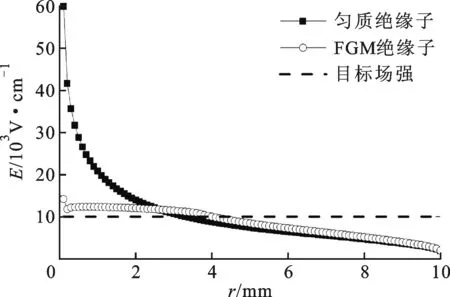


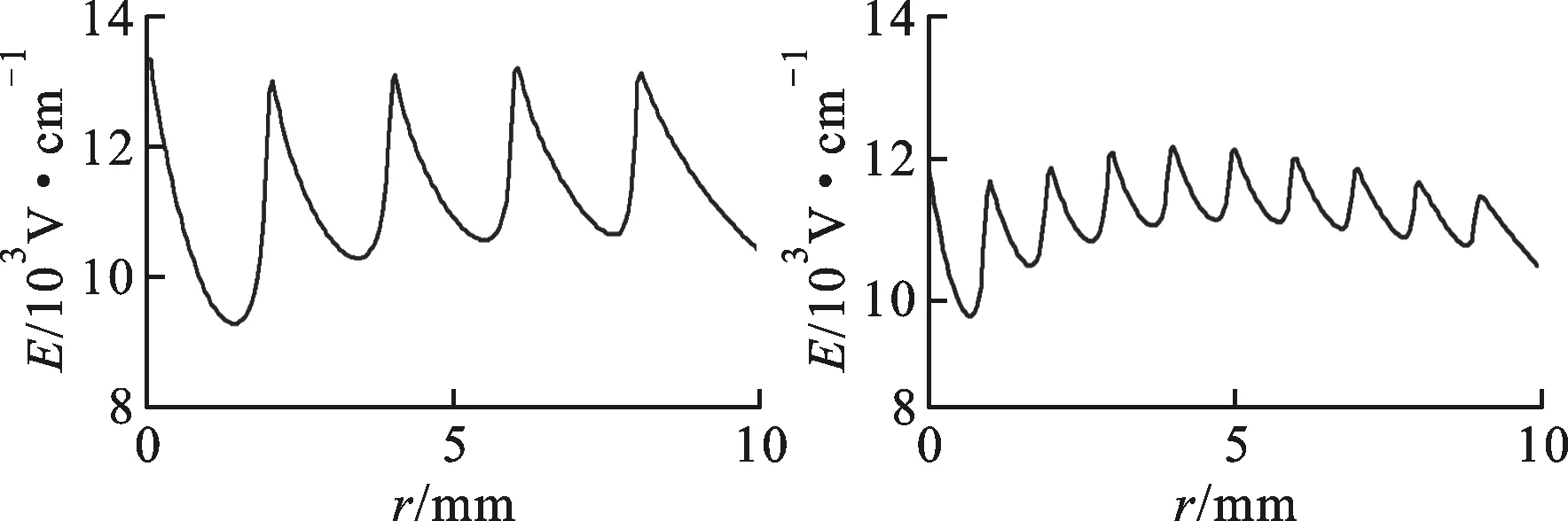

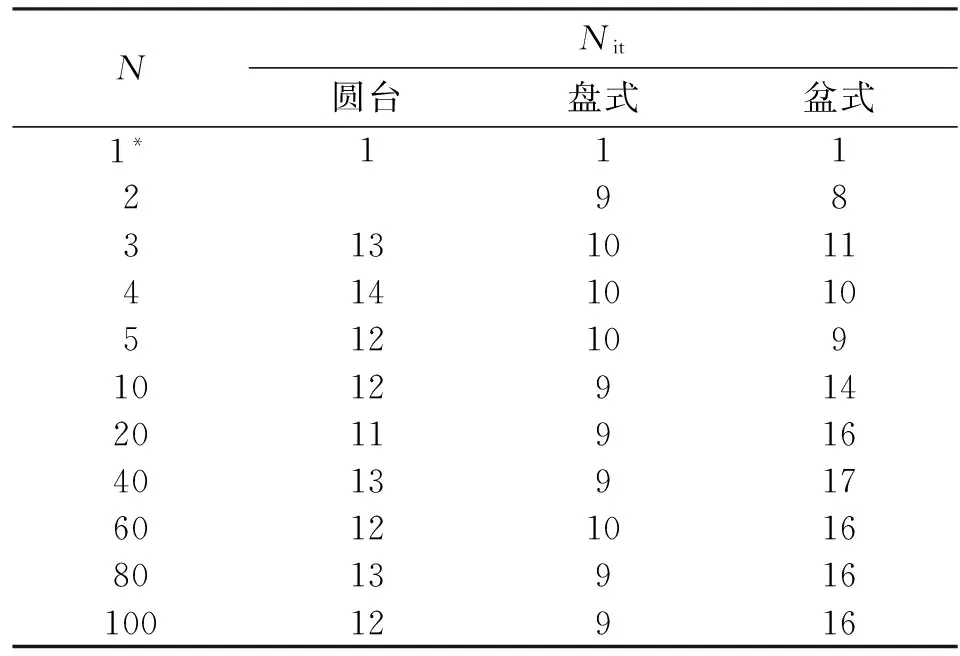

4 结 论

