采用能耗最优改进蚁群算法的自治水下机器人路径优化

刘贵杰,刘鹏,穆为磊,王寿军

(中国海洋大学机电工程系,266100,山东青岛)



采用能耗最优改进蚁群算法的自治水下机器人路径优化

刘贵杰,刘鹏,穆为磊,王寿军

(中国海洋大学机电工程系,266100,山东青岛)

针对传统路径优化算法中“距离最短能耗非最低”的问题,提出了一种基于能耗最优改进蚁群算法的自治水下机器人路径优化算法。该算法通过对水下机器人进行水动力学分析,建立了水下机器人移动过程中的受力模型;得到了机器人移动路径的能耗计算公式;提出了能耗最优的改进蚁群算法,采用路径能耗的倒数作为路径信息素值,实现了能耗指导蚁群进化的目的。实验结果表明:该算法规划的路径长433.51 m,水下机器人能耗12 235.17 J,算法寻优迭代次数22次;传统距离最优算法规划的路径长393.56 m,水下机器春能耗12 864.99 J,算法寻优迭代次数33次。该算法规划的路径距离虽比传统算法长10%,但是能耗却降低了5%,收敛速度明显比传统算法快,对降低水下机器人能耗、提高续航能力有一定的优势。

能耗;蚁群算法;自治水下机器人;距离

自治水下机器人(autonomous underwater vehicle,AUV)具有高自动化和智能化的特点,可以独立自主地完成水下作业任务和水下巡航。路径规划是一种典型的优化问题,也是水下自治机器人领域的研究热点,按照某一性能指标(最小工作代价、最短路径等)得到一条最优的水下路径对水下自治机器人具有重要的意义[1]。通常情况下,AUV优化路径评价指标包括时间最优、距离最优、能耗最优,但是AUV的能源需要自身携带,从而限制了水下机器人的行动范围和工作时间,因此在AUV巡航过程中寻找一条能耗最低的优化路径具有重要的实用价值。

在机器人路径规划的算法领域中,常用的全局路径规划方法很多,例如栅格法[2]和人工势场法[3]。栅格法思想简单,但是栅格粒度划分与计算复杂度之间很难找到平衡点;人工势场法模型简单、计算量小且实时性好,但是容易产生局部最优解问题和死锁现象。随着智能控制技术的发展,出现了A*算法[4]、遗传算法[5]、蚁群算法[6]、人工鱼群算法[7]、粒子群算法[8]和免疫算法[9]等。蚁群算法是一种群体智能随机优化算法,具有正反馈、分布式计算,较强的通用性和鲁棒性等特点。

传统路径规划研究以距离最短为目标函数,选取距离最短的路径作为最优的路径。这种方法假设机器人移动过程中能耗与移动距离成正比关系,不考虑机器人加减速、转弯等过程的影响,然而水下AUV移动时存在加减速、定速巡航和转弯等过程,因此,距离最短的路径不一定是能耗最低的路径。

为了使水下AUV获得能耗最小的优化路径,从而为AUV长时间巡航提供理论基础,本文提出以能耗最低为目标函数,通过建立AUV运动的速度模型和能耗模型,获得AUV规划路径的总能耗,并采用路径能耗更新蚁群算法的信息素,实现路径向能耗最小的方向进化。

1 拐点速度和总能耗的计算方法

为了准确求解AUV路径的总能耗,首先需要建立AUV移动速度模型,然后根据水阻力、推进器推力和效率的计算公式,求得AUV移动时规划路径的总能耗。

1.1 巡航速度模型

为了简化计算过程的复杂度,忽略AUV移动路径中的加减速过程,并做如下假设:①AUV匀速开始直线航行,中间转弯采用低速航行,最终以匀速到达终点;②AUV由直线航行状态进入转弯航行状态以及由转弯航行状态重新进入长直线航行状态时忽略加减速过程。距离拐角顶点两侧各5 m处为转弯航行阶段。因此,AUV巡航过程可划分为直线匀速航行和转弯匀速航行2种,如图1所示,其中长直线航行速度取2.5 m/s。

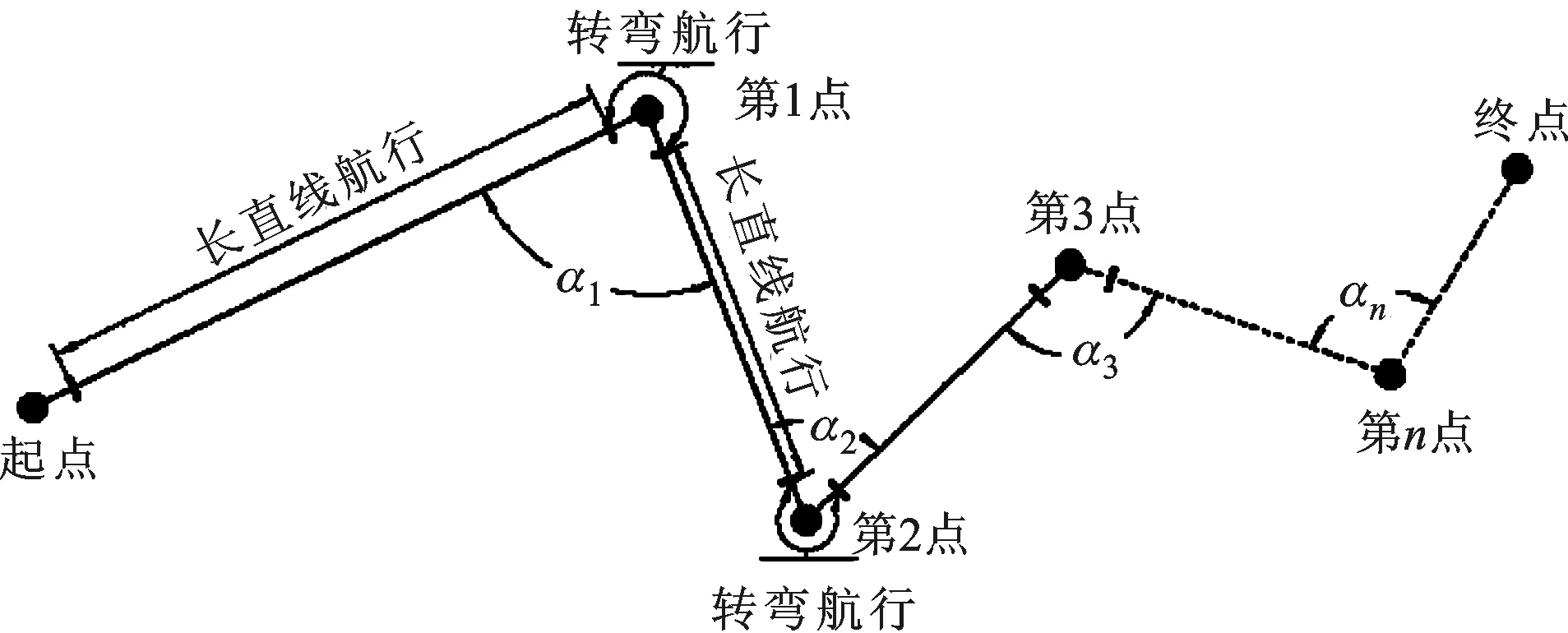
图1 速度模型示意图

AUV在转弯时必定要适当减速,因此AUV的转弯速度低于其做长直线运动时的速度。本文假设不同的转弯角度对应不同的转弯速度,对应关系为

vi=0.01αi+0.7

(1)

式中:vi为转弯速度;αi为转弯角度,范围为0°<αi≤180°。

AUV在巡航过程中,巡航过的任意连续3个点可以构成一个三角形,以中间点为顶点的角为三角形的一个内角,如图1中α1,α2,α3,…,αn所示。

1.2 水阻力的计算

AUV在水下航行时受到水阻力,根据水动力学公式,得出机器人受到的水阻力为

F=1/(2Cρv2S)

(2)

式中:F为AUV航行时受到的水阻力;C为水动力系数,C的取值不仅与介质性质有关,还与机器人形状、迎流面积等一系列要素有关,根据经验一般取0.7;ρ为水的密度;v为AUV的航行速度;S为AUV的横截面积,实验样机的横截面积为0.035 m2。

由式(2)得

v=(2F/Cρs)1/2

(3)

在AUV匀速移动时水阻力F与推进器产生的推力FT相等,故由推进器的推力可求得匀速航行状态下AUV的航行速度。

AUV在水下巡航时克服水阻力做功,如忽略AUV推进器之外的部件发热和能耗,AUV能量的消耗为克服水阻力做功,故在计算能量消耗问题时所有能耗均用来克服水阻力做功。

1.3 推进器的推力曲线

本文针对研究团队研发的AUV样机的巡航问题开展研究。该样机采用TECNADYNE公司的Model 150推进器,该推进器为无刷直流电机,通过改变供电的占空比达到调速的目的。

由牛顿第二定律可知,AUV恒速航行时所受的合力为零,此时推进器产生的推力与水阻力相等。为了获得推进器的推力曲线,搭建了推进器测试平台,获得的推进器推力曲线如图2所示。

图2 推进器推力曲线

1.4 速度与效率的关系

Model 150推进器采用无刷直流电机,由无刷直流电机特有的机械特性可知,在一定转速范围内,随着电机转速的提高,机械效率逐渐提高,而无刷直流电机的转速又影响到AUV的航行速度。假设AUV的能量消耗全部转化为AUV推进器无刷直流电机的能量消耗,那么推进器无刷直流电机的效率直接决定了AUV的工作效率,因此AUV的航行速度与AUV的工作效率存在如下关系

ηi=FTivi/Pi

(4)

式中:ηi为AUV的工作效率;FTi为推进器推力;vi为AUV的航行速度,可由式(1)求出;Pi为输出功率。

图3 AUV速度效率曲线

为预测任意速度下AUV的工作效率,用三次函数拟合AUV航行速度与AUV工作效率曲线,得AUV航行速度vi与AUV的工作效率为

(5)

1.5 能耗计算

假设AUV在巡航过程中以2.5 m/s的初速度从起点出发,经过中间各点之后最终以2.5 m/s的速度到达终点。整个运动过程分解为5个长直线航行与转弯航行的组合以及倒数第二个巡航点与终点的长直线航行,由此运动过程计算能量消耗。

AUV在匀速航行过程中消耗的能量为

E=Pt/η=Fvt/η=FL/η

(6)

将式(1)代入式(6)得

E=Cρv2SL/2η

(7)

将式(5)代入式(7)得运动过程中的总能耗为

(8)

当vi≠0时,式(8)等价于

∑E=∑0.5CρSL/(-0.073vi+

(9)

令

(10)

由式(6)、式(9)、式(10)可得

∑E∝L/f(vi)

(11)

做函数f(vi)趋势曲线,如图4所示。

图4 f(vi)趋势曲线

由式(11)可知,AUV的能耗只与AUV的航行速度和航行距离有关,因此在研究AUV能耗问题上将速度与距离作为直接研究对象。由图4分析可知,在AUV最大航速2.5 m/s的范围内,速度越高能耗越低。

2 基于能耗最优的改进蚁群算法

蚁群算法是模拟自然界中蚂蚁的觅食行为而形成的一种群体智能优化算法。蚂蚁在寻找食物的过程中会释放信息素,而且在寻找食物的过程中会根据信息素强度指导下一步的移动方向。一条路径上信息素浓度越高就表明该路径上通过的蚂蚁的数量越多,其他蚂蚁选择该路径的可能性越大。

2.1 算法实现步骤

步骤1 参数设置。本文中为体现路径以能耗最优为主,因此设置信息启发式因子α=1.5,期望启发式因子β=1,信息素挥发因子Δ=0.1。对每一代蚂蚁来说,将允许搜索的点加入allowed表中,将已巡航的点加入禁忌表tabu中,并在各因子的作用下指导蚂蚁寻找路径,最终获取每一代蚂蚁的最优路径。

步骤2 种群初始化。一般地,种群中个体越多,求出的最优解的品质越好,但是计算量也越大。为了兼顾求解效率和求解品质,蚂蚁个体数m取为20,种群进化代数取为50。

(12)

式中:t为蚂蚁编号;i、j、k表示蚂蚁当前处于j点,i为j之前经过的点,k为j之后待搜索点,k∈allowed;τijk(t)为信息素因数,由能耗决定;δjk(t)为能见度因数,由距离决定。

直到该蚂蚁到达终点为止,一个蚂蚁个体完成一次路径搜索。

步骤4 更新信息素。每个蚂蚁个体完成一次路径搜索后进行一次信息素更新,信息素更新为

τ(t+1)=(1-Δ)τ(t)+Δτ(t)

(13)

步骤5 终止条件。当50代蚂蚁全部完成搜索后,算法终止。在每一代的搜索过程中记录算法寻找的最优路径,最终对比50代蚁群寻找出最优路径进行输出,完成路径搜寻。

2.2 算法关键要素

在每一代蚁群中第一个蚂蚁进行搜索时,各巡航点之间的信息素均为1。当每只蚂蚁搜寻完所有路径点后进行信息素更新,信息素的更新由能量决定

(14)

式(14)表明,路径的总能量影响到信息素的更新。将式(14)代入式(10)中完成信息素更新。路径能耗越低,信息素的积累量越大,下一只蚂蚁选择低能耗路径的可能性就越大。

能见度因数δjk(t)由j、k两点间的距离djk决定

δjk(t)=1/djk

(15)

两点之间的距离越小,能见度因数就越大,蚂蚁的选择概率越高。

3 仿真实验及分析

3.1 巡航点地图

选取如图5所示的海域地图为测试对象,地图中包含11个巡航点,巡航点坐标见表1。要求AUV从起点出发遍历所有目标点并最终到达终点。

图5 海域巡航点地图

巡航点x/my/m113.0423.12237.1213.99323.7029.75425.6217.56537.1516.78637.8022.12740.2928.38835.0723.67933.9426.431031.4035.501143.865.70

3.2 实验结果及分析

将以上参数输入至改进蚁群算法中,经过50代蚂蚁的搜寻,得到能耗最少的遍历所有巡航点的路径,如图6所示。在此路径下,AUV航行距离为433.51 m,能耗为12 235.17 J。

图6 能耗最优蚁群算法规划路线

为了验证本文算法的优越性,针对同一巡航地图,采用同样的蚁群参数进行了路径优化,得到了基于传统距离最优算法的最优路径,如图7所示。在此路径下,AUV航行距离为393.56 m,能耗为12 864.99 J。

图7 距离最优蚁群算法规划路线

算法求解过程记录每次迭代寻优路径的最小能耗和平均能耗,通过算法最优迭代次数比较本文提出的基于能耗最优改进蚁群算法和传统的基于距离最优蚁群算法的收敛速度。图8所示为基于能耗最优改进蚁群算法的寻优过程,图9为基于距离最优蚁群算法的寻优过程,两种算法的对比见表2。

图8 能耗最优改进蚁群算法的寻优过程

图9 传统距离最优蚁群算法的寻优过程

算法质量的好坏会影响程序执行效率。时间复杂度和空间复杂度是评价算法性能的重要指标[10],在蚁群优化算法中其评价指标公式可做如下简化[11]。时间复杂度是巡航点的四阶函数,记为O(n4)

O(n4)=n(n-1)mT/2

(16)

空间复杂度是巡航点的二阶函数,记为O(n2)

O(n2)=3n2+nm

(17)

式中:n为巡航点数;m为蚂蚁数;T为迭代次数。

表2 能耗、距离最优蚁群算法的对比

从表2仿真结果来看,基于能耗最优改进蚁群算法得到的路线航行距离为433.51 m,比基于传统距离最优算法得到的路线航行距离393.56 m长10%。然而,基于能耗最优改进蚁群算法的路线能耗为12 235.17 J,比传统算法路线能耗12 864.99 J低5%,从收敛速度来看,本文提出的改进算法在寻优迭代22次开始收敛,而传统算法迭代33次才开始收敛,两种算法的空间复杂度评价值相同,但是本文改进算法的时间复杂度评价值要远小于传统算法的时间复杂度评价值。

4 结 论

(1)AUV路径规划问题中实现低能耗才是最终目的。本文提出了一种基于能耗最优改进蚁群算法的水下AUV路径优化算法,该方法从AUV的工作效率作为切入点,从能耗因素来考虑AUV的路径规划问题,从仿真实验结果可以看出,本文提出的规划算法比传统的基于距离最优规划算法得到的路线虽然距离长一些,但是能耗却更低,从而有利于提高AUV的续航能力。本文提出的改进算法以能耗最小为主,距离较短为辅,使寻优路径趋向于能耗最低、距离较短的优化路径,由于优化参量的增加,缩小了蚁群搜索空间,从算法的复杂度分析,本文提出的优化算法的时间复杂度评价值比传统算法大幅减小,有利于提高算法收敛速度。

(2)本文提出的能耗最优算法虽然较好地实现了AUV的更低能耗,但是在算法的实现过程中忽略了AUV的加减速过程,会对最优结果求解产生影响。接下来会考虑加减速过程对AUV能耗的影响。

[1] YUAN Mingxin, WANG Sun’an, WU Canyang, et al. Hybrid ant colony and immune network algorithm based on improved APF for optimal motion planning [J]. Robotica, 2010, 28(6): 833-846.

[2] 王醒策, 张汝波, 顾国昌. 基于势场栅格法的机器人全局路径规划 [J]. 哈尔滨工程大学学报, 2003, 24(2): 171-174. WANG Xingce, ZHANG Rubo, GU Guochang. Potential grid based global path planning for robots [J]. Journal of Harbin Engineering University, 2003, 24(2): 171-174.

[3] 李擎, 王丽君, 陈博. 一种基于遗传算法参数优化的改进人工势场法 [J]. 北京科技大学学报, 2012, 34(2): 202-206. LI Qing, WANG Lijun, CHEN Bo. An improved artificial potential field method with parameters optimization based on genetic algorithms [J]. Journal of University of Science and Technology Beijing, 2012, 34(2): 202-206.

[4] 王殿君. 基于改进A*算法的室内移动机器人路径规划 [J]. 清华大学学报(自然科学版), 2012, 52(8): 1085-1089. WANG Dianjun. Indoor mobile-robot path planning based on an improved A*algorithm [J]. Journal of Tsinghua University (Science and Technology), 2012, 52(8): 1085-1089.

[5] 石铁峰. 改进遗传算法在移动机器人路径规划中的应 [J]. 计算机仿真, 2011, 28(4): 193-195. SHI Tiefeng. Research on path planning for mobile robot based on improved genetic algorithm [J]. Computer Simulation, 2011, 28(4): 193-195.

[6] 张银玲, 牛小梅. 蚁群算法在移动机器人路径规划中的仿真研究 [J]. 计算机仿真, 2011, 28(6): 231-234. ZHANG Yinling, NIU Xiaomei. Simulation research on mobile robot planning based on ant colony optimization [J]. Computer Simulation, 2011, 28(6): 231-234.

[7] 周利坤, 刘宏昭. 自适应人工鱼群算法在清罐移动机器人路径规划中的应用 [J]. 机械科学与技术, 2012, 31(7): 1085-1089. ZHOU Likun, LIU Hongzhao. An adaptive artificial fish school algorithm for path planning of mobile tank-clearing robot [J]. Mechanical Science and Technology, 2012, 31(7): 1085-1089.

[8] 李擎, 徐银梅, 张德政. 基于粒子群算法的移动机器人全局路径规划策略 [J]. 北京科技大学学报, 2010, 32(3): 397-402. LI Qing, XU Yinmei, ZHANG Dezheng. Global path planning method form mobile robots based on the particle swarm algorithm [J]. Journal of University of Science and Technology Beijing, 2010, 32(3): 397-402.

[9] 叶兆莉, 袁明新, 程帅. 移动机器人的一种烟花爆炸式新免疫规划算法 [J]. 计算机仿真, 2013, 30(3): 323-326. YE Zhaoli, YUAN Mingxin, CHENG Shuai. New fireworks explosive immune planning algorithm for mobile robots [J]. Computer Simulation, 2013, 30(3): 323-326.

[10]张宇山. 进化算法的收敛性与时间复杂度分析的若干研究 [D]. 广州: 华南理工大学, 2013: 10-17.

[11]傅鹏. 多目标广义蚁群算法的收敛性、收敛速度和算法复杂度研究及其应用 [D]. 南京: 南京邮电大学, 2014: 16-32.

(编辑 武红江)

A Path Optimization Algorithm for AUV Using an Improved Ant Colony Algorithm with Optimal Energy Consumption

LIU Guijie,LIU Peng,MU Weilei,WANG Shoujun

(Department of Mechanical and Electrical engineering, Ocean University of China, Qingdao, Shandong 266100, China)

A path optimization algorithm for autonomous underwater vehicles is proposed to solve the problem of the shortest distance with not the lowest energy consumption in the traditional path optimization algorithm. The algorithm bases on an improved ant colony algorithm with optimal energy consumption. A stress model of movement process of AUV in water is built by studying the hydrodynamic analysis of AUV and a formula to calculate the energy consumption of AUV moving path is derived. Then, the improved ant colony algorithm with optimal energy consumption is presented. The inverse of the path energy consumption is used as a path pheromone value to guide evaluation of ant colonies by energy consumption. Experimental results show that the proposed algorithm uses 22 iterations to plan a 433.51 m long path with 12 235.17 J AUV energy consumption, while a traditional algorithm uses 33 iterations to plan a 393.65 m long path with 12 864.99 J AUV energy consumption. The path distance planned by the proposed algorithm is 10% longer than that planned by the traditional algorithm, but it's energy consumption is lower by 5%. It is clear that the algorithm has advantages of reducing the energy consumption and improving the battery life.

energy consumption; ant colony algorithm; autonomous underwater vehicle; distance

2016-03-15

刘贵杰(1968—),男,教授;穆为磊(通信作者),男,讲师。

国家自然科学基金资助项目(61540010,61501418)。

时间:2016-09-02

http:∥www.cnki.net/kcms/detail/61.1069.T.20160902.1630.008.html

10.7652/xjtuxb201610014

TP242

A

0253-987X(2016)10-0093-06