一种用于虹膜识别的特征提取算法

来 毅, 王 倩, 刘 颖, 李大湘

(西安邮电大学 通信与信息工程学院， 陕西 西安 710121)



一种用于虹膜识别的特征提取算法

来 毅, 王 倩, 刘 颖, 李大湘

(西安邮电大学 通信与信息工程学院， 陕西 西安 710121)

通过对比分析2维(2D)复Gabor滤波器实部和虚部幅频的响应特性，给出一种基于2D奇Gabor滤波的虹膜特征提取算法。根据2D奇Gabor滤波器关于原点奇对称，利用其编码虹膜纹理特征点的相位信息，计算汉明距离，实现虹膜分类识别。实验结果表明，所给算法可使系统识别错误率降低约12%。

虹膜识别；特征特取；Gabor滤波器

虹膜识别作为一种新颖的基于生理特征的识别方法[1]，是以人眼的虹膜为特征，通过区分人眼虹膜纹理信息进行有效的身份鉴别。虹膜识别的关键是特征提取和匹配[2]，其结果直接决定了虹膜识别系统的性能[3]。虹膜识别算法通常都是采用2维(2D)复Gabor滤波的方法，对虹膜纹理的相位特征进行编码[4]，但2D复Gabor滤波器的实部含有直流分量且易形成低通滤波器，无法有效提取虹膜纹理特征。

本文拟利用2D奇Gabor滤波器，对归一化后的虹膜图像进行滤波，再对滤波后的相位信息进行编码，并通过计算虹膜间的汉明距离进行匹配。

1 Gabor滤波器

虹膜图像本质上是一种纹理图像，从中提取纹理特征的有效方法之一，就是将图像与带通滤波器进行卷积。由于2D Gabor滤波器能够很好地模拟皮层简单细胞的二维感受轮廓，最大限度地提供图像的方向信息和频率信息，同时也能够提取位置信息[5]，因此，实际应用中带通滤波器通常选择2D Gabor滤波器。

2D复Gabor滤波器在空频域的形式可描述为[6]

(1)

其中,(x0,y0)是滤波器的中心点坐标，f0是滤波器的中心频率,θ0是滤波器方向,α和β是空间参数。

由式(1)分析可知，G(x,y)函数被局限在Gauss窗内。在窗口内，G(x,y)与人的视觉感知细胞的2D接收域波形非常相似[4]。通过调整G(x,y)的参数(x0,y0,f0,θ0,α,β)，可使Gabor函数具有各种不同的空间特征，如方向选择性与频率选择性等。为了简单起见，取

x0=0, y0=0, α=β=σ,

则式(1)简化为

G(x,y)=he(x,y)-i ho(x,y)。

(2)

其中

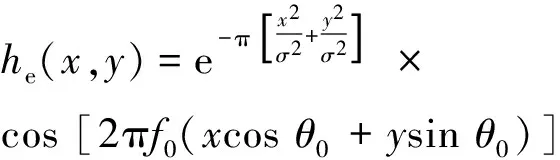
(3)

(4)

分别为G(x,y)的偶部(即实部)和奇部(即虚部)，其Fourier变换分别为

(5)

(6)

其中带通滤波器

H1(u,v)=σe-πσ2[(u-f0cos θ0)2+(v-f0sin θ0)2],

(7)

H2(u,v)=σe-πσ2[(u+f0cos θ0)2+(v+f0sin θ0)2],

(8)

关于原点偶对称，故He(u,v)由关于原点偶对称的两个带通滤波器形成，Ho(u,v)由关于原点奇对称的两个带通滤波器形成 。

Gabor滤波器频率的半峰带宽可描述为[7]

σf0=c(常数)。

即当f0较大时，σ比较小，滤波器带宽变宽，此时构成He(u,v)的两个带通滤波器在低频部分叠加容易形成低通滤波器，这种情况十分不利于虹膜纹理特征的提取。然而,H1(u,v)和-H2(u,v)关于原点是奇对称的，此时恰好在低频部分相互抵消，故在任何情况下，由它们构成的Ho(u,v)都是一个很好的带通滤波器。设置适当的f0，则Ho(u,v)可滤除低高频分量，降低图像中的噪声，从而有效地提取虹膜纹理特征。

中心频率f0较小或较大时，2D Gabor滤波器偶部和奇部的的空频域波形和幅频响应分别如图1和图2所示。在图1中，Gabor滤波器偶部和奇部都是较好的带通滤波器，而在图2中，2D Gabor滤波器偶部形成了低通滤波器，但其奇部依然为带通滤波器，因此，采用2D奇Gabor滤波器，即2D Gabor滤波器的虚部，可有效地提取虹膜纹理特征。

图1 f0较小的情形

图2 f0较大的情形

2 虹膜识别

通常获取到的虹膜图像包含很多无效信息在内，如图3(a)，且虹膜每次在图像中的位置、大小和旋转角度都不一定相同。可靠有效的虹膜识别算法应具有平移、缩放及旋转不变性。新算法将通过对图像预处理，实现对平移及缩放的补偿，并利用移位匹配虹膜特征模板完成旋转补偿。

2.1 虹膜图像预处理

为了使虹膜识别算法满足平移和缩放不变性，在采集到的原始虹膜图像中定位虹膜,并将其归一化:虹膜定位是指确定虹膜区域的内外边界;虹膜图像归一化则是通过坐标映射，将不同尺寸的虹膜图像调整为固定尺寸，以便后续处理。为此，可采用文献[4]所述方法进行虹膜定位及归一化，相关结果如图3所示。

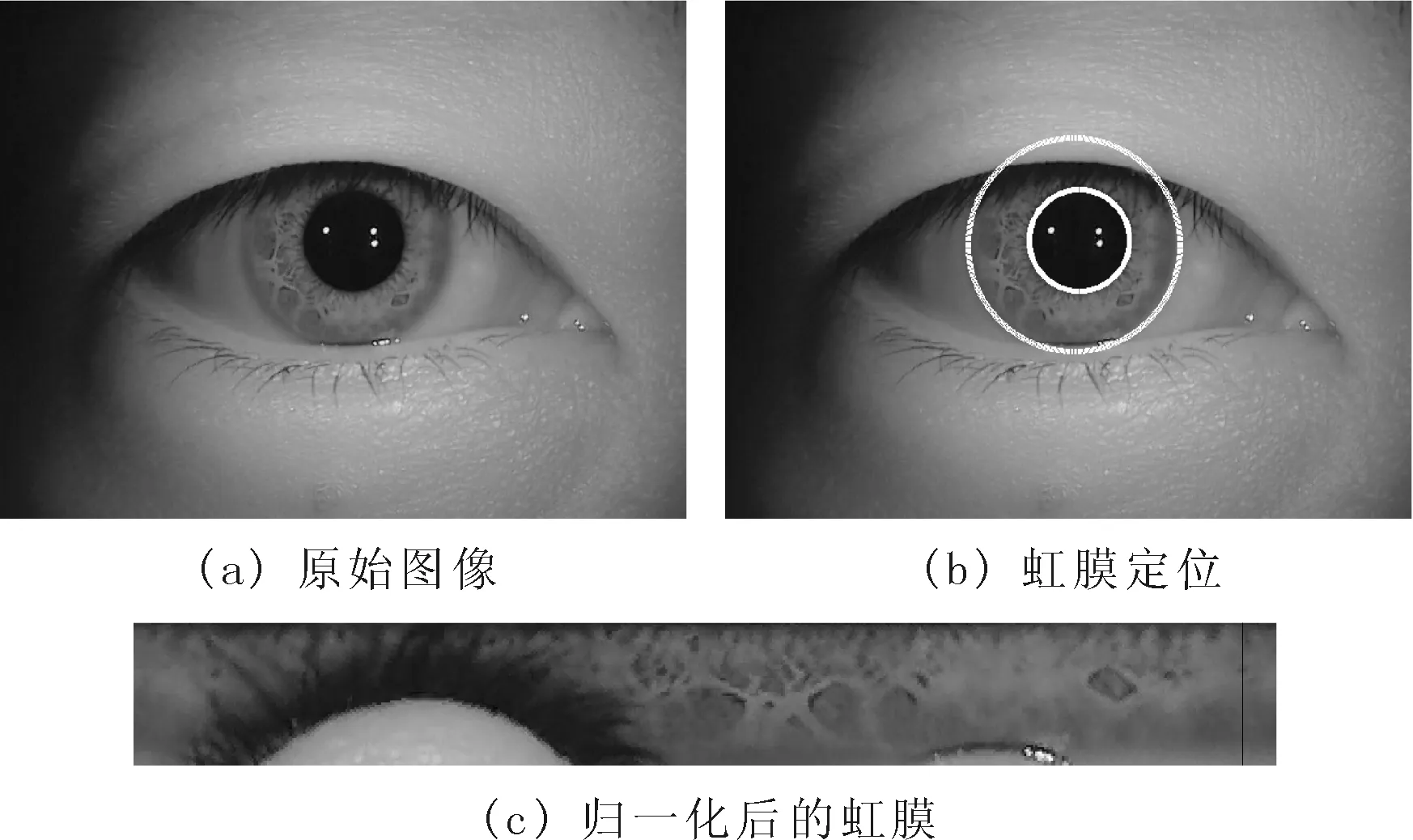
图3 虹膜图像预处理

2.2 虹膜特征提取及编码

假设归一化后的虹膜图像为P(x,y)。虹膜的纹理特征在P(x,y)接近水平的方向具有较高的信息密度和很强的区分性[8]，故只需在θ0方向提取特征,即可满足虹膜识别的需要。根据式(4)，提取虹膜纹理特征的滤波器组可表示为

(9)

其中i=0,1,2,3。实验时，滤波器中心频率fi依次分别取3,6,12和24。

通过使用2D奇Gabor滤波器组提取虹膜特征后，对滤波结果的相位信息进行编码，即

(10)

式中,bi(x,y)为点(x,y)处的编码结果，“*”代表卷积，i=0,1,2,3。

2.3 虹膜匹配

在虹膜特征二值化编码的模板匹配中，汉明距离(Hamming distance，HD)是效果较好的模板匹配方法。借助汉明距离，可通过计算两个模板间对应的位是否一致来实现匹配。此法计算量小，实时性好，简单易用，完全可以满足虹膜识别的匹配需求。

假设码长为L字节，虹膜特征码A和B的归一化汉明距离可以表示为

(11)

其中“⊕”表示异或运算，Aj为待识别图像特征码的第j个码字，Bj为模板图像特征码的第j个码字。当Aj和Bj对应的比特位不同时，则计算结果为1，当Aj和Bj对应的比特位相同时，则计算结果为0。因此，若两幅虹膜图像是采集于同一个人的同一只眼睛，则dH=0；当两幅虹膜图像是采集于不同人的眼睛或同一人的不同眼睛，则dH=1。

3 实验结果及分析

为验证所给新算法的有效性和可靠性，采用识别难度较大的虹膜图像库——第一届中国生物特征识别竞赛训练库1[9]——进行实验。该虹膜图像库包括30个人，每人左眼和右眼各20幅图，共60类，1 200幅虹膜图像，图像的分辨率为640×480。

实验在认证模式下进行。在认证模式的算法测试中，输入数据声称自己是来自某一特定的类别，目的在于测试算法是否能够正确判断该输入数据来自所声称的这一类别。测试时常采用3个指标来衡量一个系统识别性能，即错误接受率(False Acceptance Rate, FAR)，错误拒绝率(False Rejection Rate, FRR)和等错误率(Equal Error Rate, EER)。其中EER数值越小，说明算法的性能越好。

实验分别采用2D奇Gabor滤波器和2D复Gabor滤波器的方法，提取虹膜纹理特征点相位信息，并将测试结果进行对比。“算法A”采用基于2D奇Gabor滤波器，“算法B”采用基于2D复Gabor滤波器。两种算法识别性能的对比结果如图4所示。实验中眼睑和眼睫毛遮挡等其它噪声均未考虑，只是通过平移匹配虹膜特征模板来实现旋转补偿。考虑到两种算法是在同等情况下进行比较，故此类噪声的存在并不会影响比较结果。

图4 认证模式下两种算法识别结果比较

由图4可见，“算法A”的EER只有5.21%，远小于“算法B”的17.61%。其原因在于，所给新算法采用具有良好带通特性的2D奇Gabor滤波器对虹膜图像提取特征，可避免2D偶Gabor滤波器易形成低通滤波器，从而难以有效提取虹膜图像纹理特征的问题。“算法A”只采用2D复Gabor滤波器的奇部进行识别，故其计算复杂度只是“算法B”的一半。

在相同的实验条件下，分别采用两种算法对识别难度较小的CASIA虹膜图像库[10]进行测试。该图像库共有108只眼睛，每只眼睛采集有7幅图像，故共有756 幅虹膜图像。

“算法B”所得EER为9.43%，“算法A”仅为3.74%。这再次说明，所给新算法是有效和可靠的。由此也可见，所采集的图像质量对虹膜识别算法的识别结果有一定影响，即图像质量越好，EER越小，识别的准确率越高。

4 结语

引入虹膜定位和归一化，实现移位及近似的尺度缩放不变性，并采用2D奇Gabor滤波编码虹膜纹理特征点的相位信息，匹配时采用移位虹膜特征模板实现旋转补偿，由此给出一种新的虹膜特征提取算法。对第一届中国生物特征识别竞赛训练库1和CASIA虹膜图像库中图像的测试结果显示，所给基于2D奇Gabor滤波的虹膜特征提取算法识别率较高，分类有效。

[1] SHEN F，FLYNN P J． Iris crypts: Multi-scale detectionand shape-based matching[C/OL]//2014 IEEE Winter Conference on Applications of Computer Vision (WACV). [S.l.]: IEEE,2014: 977-983[2016-04-05]．http://dx.doi.org/10.1109/WACV.2014.6835998.

[2] LI H Q，SUN Z N，ZHANG M，et al． A brief survey on recent progress in iris recognition[C/OL]//Biometric Recognition:9th Chinese Conference, CCBR 2014, Shenyang, China, November 7-9, 2014. Proceedings. Switzerland: Springer International Publishing,2014: 288-300[2016-04-05]．http://dx.doi.org/10.1007/978-3-319-12484-1_33.

[3] FENG Z G，SUN X Q． Box-counting dimensions of fractal interpolation surfaces derived from fractal interpolation functions[J/OL]． Journal of Mathematical Analysis and Applications，2014，412(1) : 416-425[2016-04-05]．http://dx.doi.org/10.1016/j.jmaa.2013.10.032.

[4] DAUGMAN J G. High Confidence Visual Recognition of Persons by a Test of Statistical Independence[J/OL]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1993, 15(11):1148-1161[2016-04-05].http://dx.doi.org/10.1109/34.244676.

[5] DAUGMAN J. Demodulation by Complex-valued Wavelets for Stochastic Pattern Recognition[J/OL]. International Journal of Wavelets, Multiresolution and Information Processing,2003,1(1):1-17[2016-04-05].http://dx.doi.org/10.1142/S0219691303000025.

[6] DAUGMAN J G. Uncertainty Relation for Resolution in Space, Spatial Frequency and Orientation Optimized by Two-Dimensional Visual Cortical Filters[J/OL]. Journal of the Optical Society of America A, 1985, 2 (7): 1160-1169[2016-04-05].http://dx.doi.org/10.1364/josaa.2.001160.

[7] BOLES W W, BOASHASH B. Human Identification Technique Using Images of the Iris and Wavelet Transform[J/OL]. IEEE Transactions on Signal Processing, 2012,46(4):1185-1188[2016-04-05].http://dx.doi.org/10.1109/78.668573.

[8] MA L, TAN T N, WANG Y H, et al. Personal Identification based on Iris Texture Analysis[J/OL]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2003, 25(12):1519-1533[2016-04-05].http://dx.doi.org/10.1109/TPAMI.2003.1251145.

[9] 第一届中国生物特征识别竞赛训练库1[DB/OL].[2016-04-05].http://sinobiometrics.com/sinobiometrics%2704.htm.

[10] CASIA虹膜图像库[DB/OL].[2016-04-05].http://sinobiometrics.com/casiairis.htm.

[责任编辑:陈文学]

A feature extraction algorithm for iris recognition

LAI Yi, WANG Qian, LIU Ying, LI Daxiang

(School of Communication and Information Engineering, Xi’an University of Posts and Telecommunications, Xi’an 710121, China)

By comparing and analyzing the response characteristics of the real and imaginary parts of 2D complex Gabor filter, an algorithm of iris feature extraction based on 2D singular Gabor filter is presented. Being odd symmetric on the origin point, the 2D odd Gabor filter is used to encode the phase information of the iris texture feature points. As the Hamming distance is figured out, the pattern matching and classification can be achieved. Experimental results show that, compared to the original ones, the given algorithm can reduce the equal error rate (EER) of system identification by about 12%.

iris recognition, feature extraction, Gabor filter

10.13682/j.issn.2095-6533.2016.06.010

2016-08-08

国家自然科学基金资助项目(61601362);公安部科技强警基础工作专项资助项目(2015GABJC51)；陕西省国际科技合作与交流计划资助项目(2015KW-005)

来毅(1978-)，男，博士，工程师，从事图像处理与模式识别研究。E-mail: laiyi0614@163.com 王倩(1983-)，女，博士，讲师，从事视觉信息处理与场景分析研究。E-mail: xinrzhsh24@163.com

TP391.4

A

2095-6533(2016)06-0051-04