金属板材厚度涡流检测仿真与实验

王 悦， 王壮壮， 吴 涛， 吴啟菡， 范孟豹

(中国矿业大学 机电工程学院，江苏 徐州 221116)



金属板材厚度涡流检测仿真与实验

王 悦， 王壮壮， 吴 涛， 吴啟菡， 范孟豹

(中国矿业大学 机电工程学院，江苏 徐州 221116)

为实现对金属板材的产品质量进行准确快速的检测，利用有限元法建立了电涡流测厚系统的理论模型。仿真研究了金属板材的厚度变化对探头电感值的影响规律。经分析发现，在同一频率下探头电感值随着金属板材厚度的增加而减小,可运用建立的试验系统进行实验研究。结果表明，实验与仿真结论一致。通过拟合并分析实验结果发现，测量精度在5%以内。

电涡流检测； 仿真； 厚度测量； 最小二乘法

0 引 言

金属板材厚度是产品质量、设备服役状态的重要参数，因此准确、快速测量金属板材厚度至关重要[1-5]。射线法存在防护放射源问题，设备昂贵，且对人体有害[6]；超声法需要对试件进行表面进行光洁处理，必须使用耦合剂[7]。基于法拉第电磁感应原理的电涡流法具有灵敏度高、造价低以及可用于高温、薄管、细线和内空表面等其它检测方法难以进行检测的特殊场合等优点，在金属板材厚度检测中应用非常广泛[8-9]。

任吉林等[10]基于涡流法对碳纤维复合材料涂层厚度的测量进行了研究；武新军等[11]以厚壁磁性材料为对象，研究了基于晚期信号斜率的脉冲涡流测厚方法；雷银照等[12]通过实验数据分析，建立激励频率范围内若干频率点处线圈散射场阻抗测量值与三层导电不导磁平板结构所有分层厚度及电导率的定性关系；周德强等[13]采用脉冲涡流检测装置在铝合金板上进行厚度实验，针对目前脉冲涡流信号所提取的信号特征进行了灵敏度与线性度分析，给出了最合适的特征值。

本文建立了由探头、金属板材和空气组成的有限元仿真模型，仿真研究了金属板材的厚度参数与探头电感值之间的关系，为实验系统的搭建和实验参数的选择等提供了理论依据。在此基础上搭建了电涡流厚度检测实验系统，对仿真结果进行验证。

1 有限元建模与仿真

1.1 建立模型

涡流仿真分析的目的是能够找到探头电感值与金属板材厚度的关系，为实验系统的搭建和实验参数的选择等提供理论依据。

ANSYS有限元分析软件有着强大的分析处理和求解功能，因而在实际工程中得到广泛的应用。由于本文采用的电涡流探头为圆柱型探头，金属试件材质地均匀无缺陷，为了简化模型，可以将仿真模型简化成二维轴对称模型。运用ANSYS Maxwell软件建立由探头、被测试件及周围空气组成的涡流检测有限元仿真模型，如图1所示。

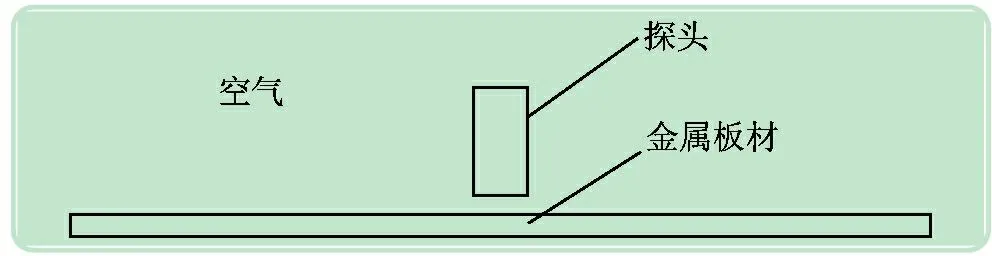
图1 仿真模型

1.2 仿真参数选取

探头由一个空心圆柱线圈组成，线圈半径20 mm，匝数为200匝，高度为60 mm。金属板材为黄铜和铝合金，厚度为0.1～1.0 mm，以0.1 mm为步长增加试件的厚度。探头置于金属板材的中心位置，距离设置为1 mm。

已知电涡流强度随金属板材深度增加作指数或近似于指数衰减，通常定义当材料内部涡流为表面涡流密度的1/e的深度为标准渗透深度[14]，如下所示:

(1)

式中:f为激励探头线圈的信号频率，Hz;σ为被测试件的电导率，S/m;μ为被测试件的磁导率，H/m;δ为标准渗透深度，m。

激励信号频率越高，涡流贯穿深度就越小，其产生的磁损耗也就越小。因此实验装置进行金属板材厚度检测时，应尽量采用较高的激励频率。但同时考虑到实验中金属板材的厚度范围为0.1～1.0 mm，根据设计经验，目标金属厚度至少为标准透射厚度的1.5倍才不会对测量结果造成显著影响[15]。结合以上因素和式(1)，将黄铜和铝合金试件的测量频率分别设定为3 kHz和5 kHz。

1.3 仿真结果与分析

电涡流探头的激励信号为频率3 kHz和5 kHz的正弦波电流信号。金属板材厚度每改变一次，得到一个探头电感值。根据仿真结果得到探头电感值随着黄铜试件和铝合金板材厚度的增加的变化趋势，如图2所示。

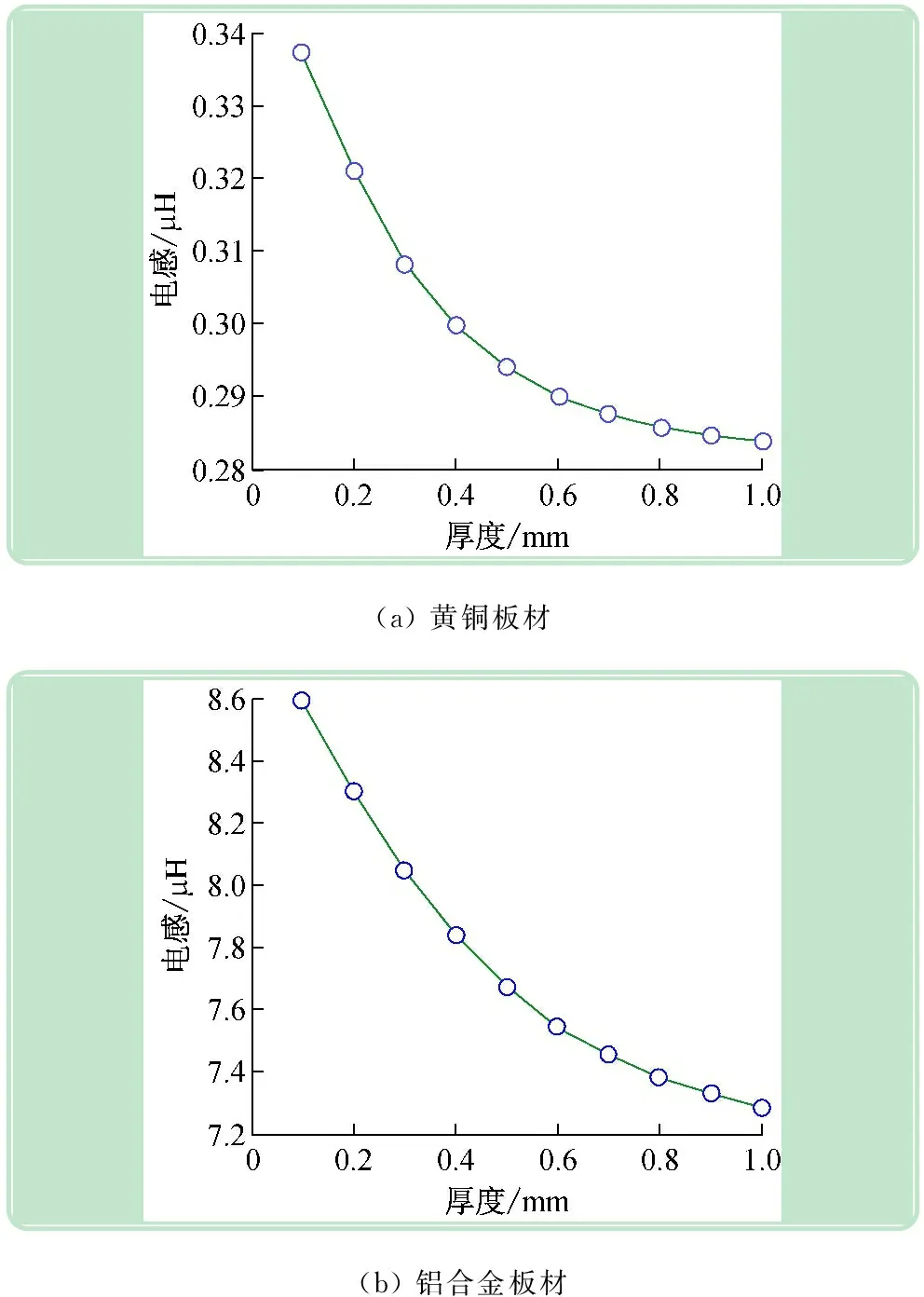
图2 黄铜、铝合金板材仿真结果曲线

由图2可知，当被测金属板材厚度在一定范围内变化时，探头线圈电感值随着金属板材的增加而减小，并且减小的趋势越来越小。下面将对这一规律进行实验验证。

2 实验验证

2.1 实验设置

搭建金属板材电涡流测厚系统由探头、65120B阻抗分析仪以及夹具组成。阻抗分析仪与探头线圈直接相连，为探头线圈提供不同频率的激励信号，并可以测试电容、电感、电抗和电阻等参数，基本测量精确度为0.05%。夹具分为基座和压板两部分，后者叠放在前者正上方并保证接触面光滑。将金属板材置于基座和压板之间，压板自身的重力作用给金属板材表面一个较大的压力，从而减小了金属板材叠加时所产生的间隙，进而减小实验误差。

根据仿真参数，设定黄铜和铝合金板材的测量频率分别为3 kHz和5 kHz，将金属板材的厚度从0.1～1.0 mm以0.1 mm为步长逐步增加，并记录下每次厚度变化后阻抗分析仪的探头电感值示数。

2.2 实验结果与分析

使用Matlab软件，用最小二乘法多项式拟合的方式对测量数据进行处理。最小二乘法是以误差的平方和最小为准则，根据观测数据估计模型中参数的一种基本参数估计方法[16]，最小二乘法多项式拟合能够得到形如下式的n阶多项式:

(2)

在曲线拟合时，一方面使曲线形状符合仿真结果中的变化规律，另一方面使曲线与各实验点之间的误差最小。故经过多次计算比较选择黄铜与铝合金板材的测量数据曲线拟合阶数n分别为6和8，曲线拟合结果如图3所示。

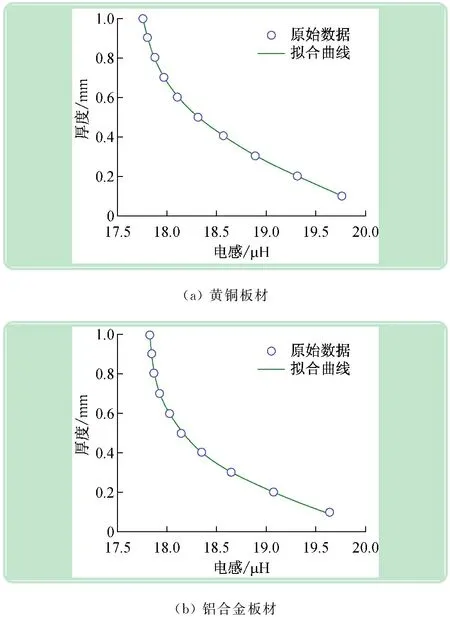
图3 黄铜、铝合金板材曲线拟合结果

根据曲线拟合结果，求得电涡流探头电感值L与金属板材厚度δ的函数关系式:

黄铜板材

(3)

铝合金板材

(4)

其中多项式系数如下:a0=9 428 200.607,a1=2 997 568.000,a2=397 035.900,a3=28 042.66,a4=1 113.935,a5=23.595,a6=0.208。b0=876 670 071 388.306,b1=377 940 469 955.667,b2=71 274 573 938.585,b3=7 679 863 256.505,b4=517 127 643.553,b5=22 282 663.462,b6=600 013.862,b7=9 231.280,b8=62.128。

通过重复实验，将测量电涡流探头的电感值作为输入参数分别代入上式计算得到被测金属板材厚度的计算值及相对误差，如表1和表2所示。

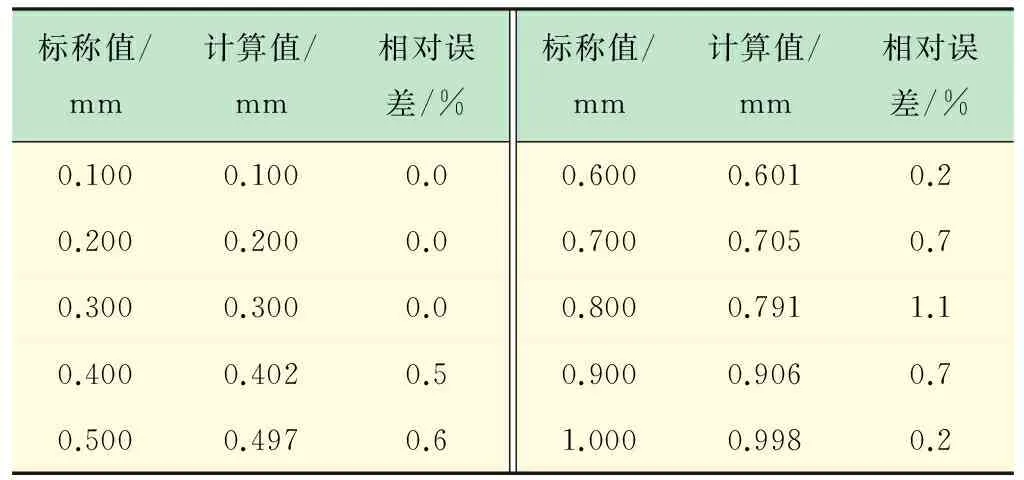
表1 黄铜板材计算值误差分析

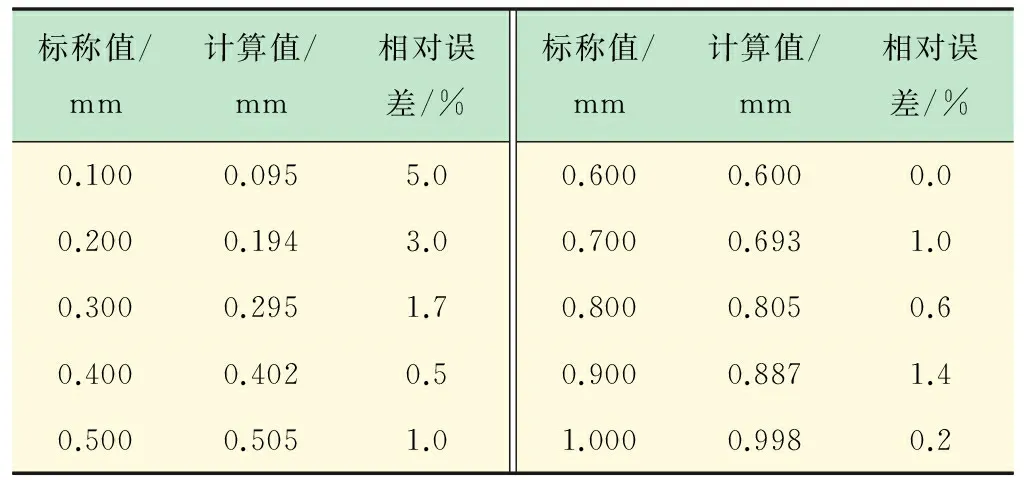
表2 铝合金板材计算值误差分析

3 结 语

本文利用有限元法建立了电涡流金属厚度检测的理论模型，通过仿真研究电涡流探头电感值与金属板材的厚度参数之间的关系。分析发现，在同一频率下电涡流探头电感值随着金属板材厚度的增加而减小。本文建立了金属板材电涡流金属厚度检测系统，经过实验验证，仿真与实验结果的规律吻合，验证了所建模型的正确性与试验系统的可行性。

本文所研究对象仅为单一材料的金属板材，下一步的研究工作将围绕金属基体上涂镀层的厚度检测。

[1] Mengbao F. Elimination of liftoff effect using a model-based method for eddy current characterization of a plate[J].Nondestructive Testing and Evaluation International, 2015(74):66-71.

[2] 段伟亮, 康 磊, 张晓辉.基于FPGA的电磁超声测厚仪[J]. 仪表技术与传感器, 2010(4): 14-16+19.

[3] Hongbo W. Noncontact thickness measurement of metal films using eddy-current sensors immune to distance variation[J]. IEEE Transactions on Instrumentation and Measurement, 2014:1-8.

[4] 魏天锋, 龚荣洲. 智能在线测厚系统的设计[J]. 仪表技术与传感器, 2006(8): 39-40,43.

[5] Syasko V A, Measuring the thicknesses of nonferromagnetic metal coatings on nonferrous metal products using the eddy-current frequency method[J]. Russian Journal of Nondestructive Testing, 2010, 46(12): 898-905.

[6] 郑 岗,刘 丁.基于提离点的脉冲涡流测厚研究[J].仪器仪表学报,2008,29(8):1745-1749.

[7] 岳秀芳,王召巴,张东利.涡流检测的厚涂层高精度方法[J].仪表技术与传感器,2014(2):99-101.

[8] Zilian Q. Improvement of sensitivity of eddy current sensors for nano-scale thickness measurement of Cu films[J]. Nondestructive Testing and Evaluation International. 2014(61):53-57.

[9] Tian S, Chen K, Bai L,etal. Frequency feature based quantification of defect depth and thickness[J]. Review of Scientific Instruments. 2014, 85(6): 64705.

[10] 任吉林.碳纤维复合材料涂层厚度涡流法测量的研究[J].仪器仪表学报,2011,32(12):2662-2668.

[11] 柯 海,武新军.基于信号斜率的铁磁材料脉冲涡流测厚研究[J].仪器仪表学报,2011,32(10):2376-2381.

[12] 任芳芳,雷银照.三层平板导体厚度及电导率的涡流检测[J].无损检测,2013,35(8):50-53.

[13] 周德强,李 勇,张秋菊. 脉冲涡流金属厚度检测信号及其特征提取[J]. 中国机械工程,2012(15):1771-1773+1778.

[14] Ribeiro A Lopes, Ramos H. Liftoff insensitive thickness measurement of aluminum plates using harmonic eddy current excitation and a GMR sensor[J]. Measurement,2012, 45(9): 2246-2253.

[15] 王旻玥, 康宜华, 叶志坚. 多通道电磁超声测厚系统[J]. 仪表技术与传感器, 2015(6): 75-76+91.

[16] Zilian Q, Qian Z, Yonggang M.In-situ measurement of Cu film thickness during the CMP process by using eddy current method alone[J].Microelectronic Engineering, 2013(108): 66-70.

·名人名言·

没有伟大的品格,就没有伟大的人,甚至也没有伟大的艺术家,伟大的行动者。

——罗曼·罗兰

Simulations and Experiments on Thickness Measurement of Metal Plates Using Eddy Current Method

WANGYue,WANGZhuang-zhuang,WUTao,WUQi-han,FANMeng-bao

(School of Mechatronic Engineering, China University of Mining and Technology, Xuzhou 221116, China)

In order to accurately and fast detect product quality, a finite element model is established by using eddy current technique to measure the thickness. Then, with the established model, the influence of thickness of the tested sheet on the probe inductance value is investigated. The simulation results show that the probe inductance value decreases when the tested sheet becomes thicker. Finally, experiments were carried out to verify this model. Experiment results show that the observations from the experimental measurements agree well with those from simulation data. Hence, this method can be used to measure the thickness of the tested sheet with small relative error (less than 5%).

eddy current testing; simulation; thickness measurement; least square method

2015-11-12

国家自然科学基金资助项目(51307172);国家级大学生创新训练计划资助项目(201410290015);江苏省自然科学基金资助项目(BK2012567);轻工过程先进控制教育部重点实验室开放课题资助项目(APCLI1404)

王 悦，男，山东滨州人，研究方向：厚度测量理论及应用。Tel.: 15150030553; E-mail: 1101730966@qq.com

范孟豹(1981-)，男，山东高唐人，博士，副教授，主要研究方向：电磁无损检测理论及应用。E-mail:wuzhi3495@cumt.edu.cn

TH 701

A

1006-7167(2016)04-0087-03