单调变分不等式的一种自适应谱梯度投影算法*
康立泉,牛善洲,黄进红
(赣南师范大学 数学与计算机科学学院,江西 赣州 341000)
·计算方法·
单调变分不等式的一种自适应谱梯度投影算法*
康立泉,牛善洲,黄进红
(赣南师范大学 数学与计算机科学学院,江西 赣州 341000)
本文提出了求解单调变分不等式问题的一种自适应谱梯度投影算法,并在一定条件下建立了算法的全局收敛性结果.初步的数值实验结果表明该算法能够有效提高原有算法的计算效率.
变分不等式;谱梯度算法;投影算法;自适应;全局收敛
1 引言
变分不等式在线性规划、网络经济、交通平衡、博弈论等领域都有非常广泛的应用.无约束优化问题在转化为变分不等式问题后,将变得更容易求解. 对于下述无约束优化问题:
(1)
其中f为连续可微可导的凸函数,Rn是n维欧式空间.上述问题的一阶必要性条件等价于一个单调变分不等式问题,即寻找u*∈Ω使得∀u∈Rn,满足
(2)
其中Ω是Rn中的一个非空闭凸集,F为Rn→Rn的连续单调算子.通常记变分不等式问题为:VI(Ω,F)问题.
投影算法是求解VI(Ω,F)问题简单且效果明显的算法,其迭代格式为:
(3)

Barzilai和Borwein提出了求解无约束优化问题的谱梯度算法也称为BB算法[7], Dai在谱梯度算法及其应用方面也做了大量的工作[8-12].进一步,Zhou和Dai提出一个自适应步长的梯度方法,实验结果表明该方法十分有效[13].此外,Yu提出了一个修正的自适应梯度算法并应用于图像去噪问题,并得到了非常好的数值表现[14].
鉴于谱梯度算法在求解优化问题上的优越表现,本文提出求解单调变分不等式问题的一种自适应谱梯度投影算法.
2 自适应谱梯度投影方法
BB算法利用当前迭代步以及前一步的信息来确定步长因子,其基本思想是利用一个数量矩阵δkI近似代替目标函数的Hessian 矩阵.Han在谱梯度算法的基础上提出了一个变分不等式问题的谱梯度投影算法迭[15]代格式为:
(4)

(5)
(6)
γ是一个大于0的常数,βk+1为步长.
为了改善上述谱梯度算法的计算效率,本文提出如下自适应交替选取大步长和小步长的方式:
(7)
具体算法如下
算法1 (自适应谱梯度投影算法:APBB)
步1: 给出初始点u0∈Rn,精度ε>0,设置最大迭代步为M及参数γ,β1;
步2: u1=PΩ(u0-β1F(u0)),设置k=1;
步3: 由(7)式计算βk+1;uk+1=PΩ(uk-γβk+1F(uk));
步4: e(uk+1)=uk+1-PΩ(uk+1-F(uk+1));
步5: 如果‖e(uk+1)‖≤ε或者k>M则迭代终止,否则设置k=k+1转步3.
3 算法收敛性分析
本文在变分不等式的框架下对于上述自适应谱梯度投影算法(APBB)进行收敛性分析.
假设1 算子F满足Lipschitz连续且强凸,即存在实数L和η使得:对于任意有u,v∈Ω有

(8)

(9)
在假设1成立的基础上,根据Cauchy-Schwarz不等式可知L>η且不等式:
(10)
成立.




由文献[16]重要投影性质可得
引理2 对于∀β1,β2,且β2≥β1>0,有
(11)
(12)
定理 通过APBB算法产生的序列{uk}全局收敛于VI(Ω,F)问题最优解.
证明 由(11)与(10)式及投影性质:
(13)
可知:
‖uk+1-PΩ[uk+1-γβk+1F(uk+1)]‖2=‖PΩ[uk-γβk+1F(uk)]-PΩ[uk+1-γβk+1F(uk+1)]‖2≤

设λ1是方程:
(14)
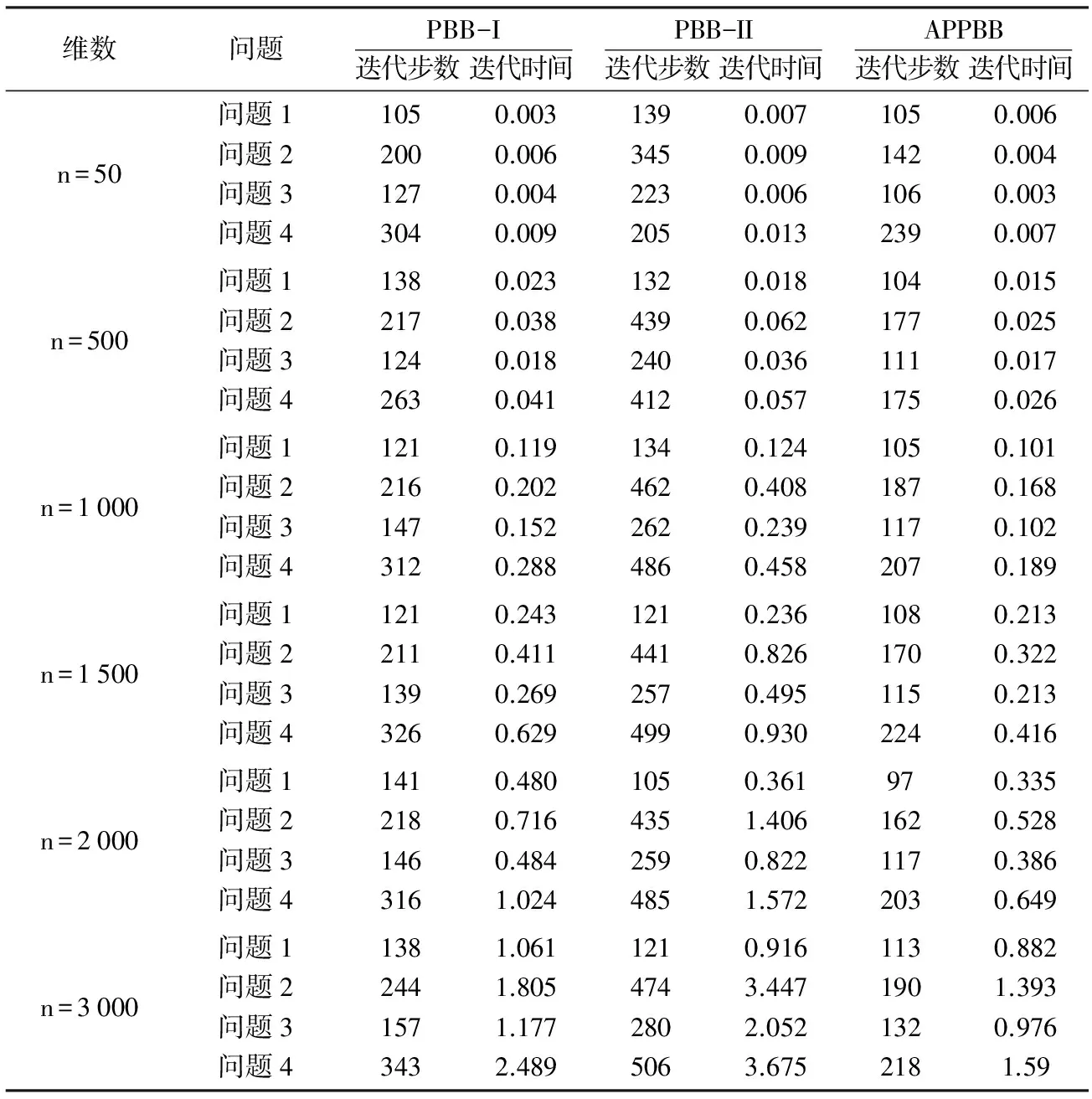
的最大实数解,其中ξ1∈(0,0.1),实数L,η满足不等式:η 因此可得: (15) 再由文献[15]引理1可知βk>η/L2,以及引理2可得: (16) 设c1=1-ξ1<1,因为βk+1 所以{uk}是柯西列且收敛于u∞.既然{u-PΩ[u-γβF(u)]}在Ω上连续,因此可得: 因为F强凸,可知变分不等式只有唯一解,即u∞=u*,所以点列{uk}收敛于VI(Ω,F)问题的最优解. 问题1 在线性互补问题中,F(u)=Mu+q其中q=(-1,-1,…,-1),在实验中条件数设定为100. 图1 APBB,PBB-I,PBB-II,算法运行时间表现图 问题2 在对称非线性互补问题中,F(u)=Mu+D(u)+q,其中Dj(u)=aj,且aj由区间(0,1)中的数随机生成. 问题3 对于上一个对称非线性互补问题2,aj由区间(-500,500)中的数随机生成. 表1 PBB-I,PBB-II,APBB算法对于互补问题实验数据结果 表2 取不同值互补问题实验数据 由表1可知:无论是迭代步还是CPU运行时间,APBB在绝大多情况下比PBB-I,PBB-II更有优势.另外,再以不同的参数γ,不同的维数n=500,n=1 500,n=3 000进行实验,代入以上四个互补问题中验证算法的有效性,从实验结果表2可知:自适应谱梯度投影算法表现优越. 为了更好说明算法APPB的效果,本节分别选用不同的初始迭代点u0=0n×1,u0=1n×1,u0=rand(n,1)再以不同的维数n为50,200,500,800进行实验,绘制出PBB-I,PBB- II,APBB三种方法相对于函数值的计算时间的表现分析图.该曲线图是根据Dolan和Moré提供的分析方法和工具,对不同算法的数值表现进行分析[18].每条曲线对应一种算法数值表现的概率分布.曲线的最左端表示该方法数值表现最有效的概率,曲线的最右端表示该方法能成功解决所有测试问题的概率.所以其它曲线右上方的曲线对应的方法是最有效和最稳定的算法.由分析图可知,APPB算法的数值表现是最好的,其中APPB算法大约对75%的测试函数CPU的计算时间是最省的,PBB-I方法大约对20%的测试函数CPU的计算时间是最省,而PBB-II法只对大约8%的测试函数CPU计算时间是最省的,从整体上看:自适应谱梯度投影算法稳定且效果好. 本文提出了求解单调单调变分不等式问题的一种自适应谱梯度投影算法,一定条件下建立了算法的全局收敛性结果.初步的数值实验结果表明该算法能够有效提高原有算法的计算效率,有一定的应用前景. [1] A.A.Goldsten. Convex programming in Hilbert space[J].Bulletin of the American Mathematical Socitey,1964,70(5):709-710. [2] E.SLevitin, B.T.Polyak. Constrained minimiztion problems[J].USSR computional Mathematics and Mathematical Physics,1966,6(5):1-50. [3] B.s. He,X.M.Yuan, J.Z.Zhang. Comparison of two kind of prediction-correction methods for monotonevaritionalinequalition[J].Computational Optimization and Applications, 2004,27(3):247-267. [4] B.S.He, X.Z.He, X.H.Liu, T.Wu. A Self-adaptive projectivon methods for co-coercive variationalinequalities[J].EuropeanJournal of Operational resarch, 2009,196(1):43-48. [5] D.R.Han, H.K.Lo. Two new self-adaptive projection methods for variational inequality problems[J].Computers and Mathematics with Applications, 2002,43(12):1529-1537. [6] D.R.Han, W.Y.Sun. A new modified Goldstein-Levitin-Polyak projection method for variational inequality problems[J].Computers and Mathematics with Applications, 2005,47(12):1817-1825. [7] J.Barzilai, J.M.Borwein. Two-point step size gradient methods[J].IMA Journal of Numerical Analysis,1988,8(1):141-148. [8] Y.H Dai, .J.Y.Yuan, Y.X.Yuan.. Modified two-point stepsize gradient methods for unconstrained optimization[J].Computational Optimization and Applications,2001,22(1):103-109. [9] Y.H. Dai, W.W. Hager, K Schittkowshi, H. Zhang. The cyclic Barzilai-Borwein method for unconstrained optimization[J].IMA Journal of Numerical Analysis,2006,26(3):604-627. [10] Y.H. Dai, .R. Fletcher. New algorithms for singly linearly constrained quadratic programs subject to lower and upper bounds[J].Mathematical Programming,2006,106(3):403-421. [11] Y.H. Dai, R. Fletcher. On the asymptotic behaviour of some new gradient meth-ods[J].Mathematical Programming,2005,103(3):541-559. [12] Y.H. Dai, R. Fletcher. Projected Barzilai-Borwein methods for large-scale box-constrained quadratic programming[J].Numerische Mathematik,2005,100(1):21-47. [13] B. Zhou. L. Gao, Y. H. Dai. Gradient methods with adaptive step size[J].Computational Optimization and Applications,2006,35(1):69-86. [14] G. H. Yu, L .Q. Qi, Y. M. Sun, Y. Zhou. Impulse noise removal by a nonmonotone adaptive gradient method[J].Signal Processing,2010,90(10):2891-2897. [15] H.J. He, D. R. Han, Z. B. Li. Some projection methods with the BB step sizes for variational inequalities[J].Journal of Computational and Applied Mathematics,2012,236(9):259-604. [16] T. Zhu, Z.G. Yu. A simple proof for some important properties of the projection mapping[J].Mathematical Inequalities and Applications,2004,7:453-456. [17] B.S. He. On the 0(1/t) convergence rate of the projection and contraction methods for variational inequalities with Lipschiz continuous monotone operators,manuscript[M].Availabl on Optimization Online,2011. [18] E. Dolan, J. Moré. Benchmarking optimization software with performance profiles[J].Mathematical Programming,2002,91(2):201-213. An Adaptive Spectral Gradient Projection Method for Monotone Variational Inequalities KANG Liquan, NIU Shanzhou, HUANG Jinhong (SchoolofMathematicsandComputerScience,GannanNormalUniversity,Ganzhou34100,China) This paper presents an adaptive spectral gradient projection method for monotone variational inequalities. Under suitable conditions, its global convergence result is established. Numberical results illustrate that the proposed method is more efficient than classical projection-like methods. variational inqualities; spectral gradient method; projection method; global convergence 2016-02-15 10.13698/j.cnki.cn36-1346/c.2016.06.003 江西省研究生创新基金项目编号(YC2014-S411) 康立泉,男,赣南师范大学数学与计算机科学学院2013级研究生;牛善洲,男,赣南师范大学数学与计算机科学学院教师,研究方向:最优化方法及其应用;黄进红,男,赣南师范大学数学与计算机科学学院教师,研究方向:最优化方法及其应用. http://www.cnki.net/kcms/detail/36.1037.C.20161209.1500.008.html O22 A 1004-8332(2016)06-0012-05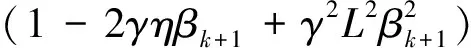

4 实验与结果

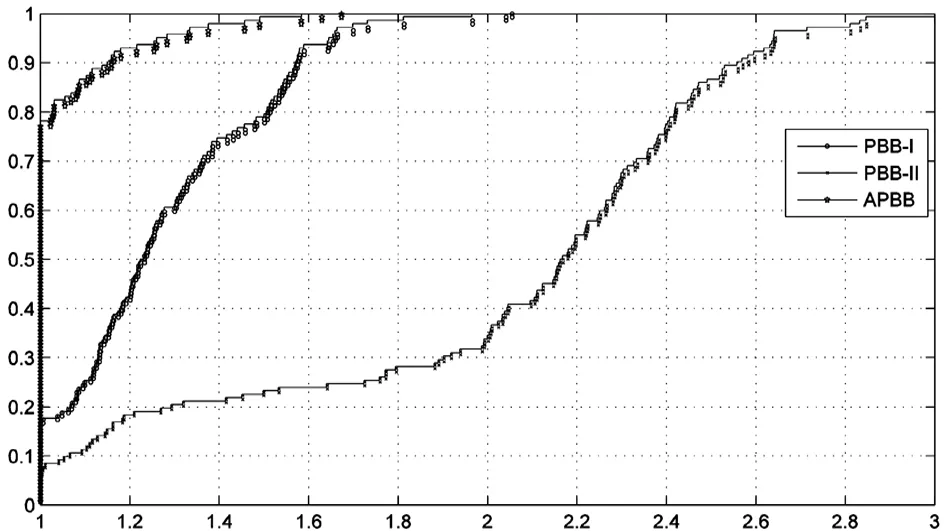


5 结论

