常红利边界下带投资的复合Poisson-Geometric风险模型

乔克林,韩建勤

(延安大学 数学与计算机科学学院,陕西 延安 716000)



常红利边界下带投资的复合Poisson-Geometric风险模型

乔克林,韩建勤

(延安大学 数学与计算机科学学院,陕西 延安 716000)

对常数红利边界策略下保费收入为复合Poisson过程,理赔支付服从复合Poisson-Geometric过程的带投资的干扰风险模型进行研究,利用全期望公式和盈余过程的马氏性,得到了直至破产时总红利现值的期望、矩母函数及其n阶矩所满足的积分微分方程。

Poisson过程; Poisson-Geometric过程; 常红利边界;积分微分方程

0 引言

风险理论是对金融保险行业所面临的各种风险进行数量分析的理论, 是经营者或决策者对各种金融或保险风险进行定量分析和预测的重要工具, 是当前精算学和数学界研究的热点, 如破产理论就是人们研究的重要课题, 并取得了许多有意义的结果[1-8], 为保险公司的稳定经营提供了理论保障。

近年来,随着金融保险行业的发展,保险业竞争越来越激烈。保险公司为了吸引更多客户投资,推出了分红保险。因此对研究红利边界策略下的风险模型无疑已成为当前研究的热点问题。1957年De Finetti[9]首次提出了红利策略;Gerber和Shui在文献[10]中考虑了带红利边界策略的经典风险模型;文献[11]研究了带利率和常数红利边界的对偶风险模型,分别给出破产为止红利现值的期望和矩满足的积分微分方程;文献[12]研究了存在红利界限和随机干扰的保费收取过程为复合Poisson过程的风险模型,得到了破产概率满足的Lundberg不等式,并给出了生存概率满足的积分微分方程; 文献[13]研究了常红利边界下保费收入为复合Poisson过程的风险模型,得到了直至破产时红利付款的期望现值、矩母函数、n阶矩以及模型的期望折现罚金函数满足的积分微分方程;文献[14]研究了常红利边界下带干扰的双复合Poisson风险模型,得到了直至破产时红利付款的期望现值、矩母函数、n阶矩以及模型的期望折现罚金函数满足的积分微分方程。

本文在上述文献的启示下,结合当前金融保险行业实际, 考虑到再投资, 随机干扰及保费为复合过程, 同时考虑到在保险事务中, 风险事件和理赔事件有可能不等价的事实, 特别是保险公司推出免赔额制度和无赔款折扣等制度的背景,建立以保费收入服从复合Poisson过程,理赔量服从复合Poisson-Geometric过程的带投资的干扰风险模型, 使其更接近保险公司的实际经营运作。

1 模型建立

定义1.1 在一个完备概率空间(Ω,F,P)上,设保险公司的盈余过程为

定义1.2 设定一红利界限b(其中b为初值且b≤u),若保险公司的盈余在红利界限b以下,则不发放红利;若盈余超过红利界限b,则超出部分全部用来分红,于是在该边界策略下的盈余过程为

dUb(t)=

定义1.3 破产时刻Tu,b=inf{t|Ub(t)<0|Ub(0)=u},若Tu,b=∞,则表示破产不会发生。

定义1.4 设D(t)为至时刻t为止保险公司的累积分红，则定义

为直至破产时的总红利现值，其中δ>0为折现因子,且对0≤u≤b,定义Du,b的均值、矩母函数和n阶原点矩分别为

V(u;b)=E[Du,b|Ub(0)=u]

M(u,z;b)=E[ezDu,b|Ub(0)=u]

其中V0(u;b)=1。

2 预备引理

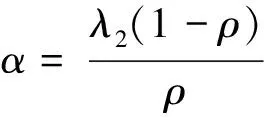
Pr(N2(t)=0)=e-λ2t=1-λ2t+o(t)

Pr(N2(t)=k)=αρkt+Ak(t)o(t) k=1,2,…

3 主要结论及证明

记F*k(y)为F(y)的k重卷积, f*k(y)为f(y)的k重卷积。并记

定理3.1 当0≤u≤b时,红利付款的期望现值V(u;b)满足的积分微分方程

当u>b时, V(u;b)=u-b+V(b;b)。

证明 当0≤u≤b时,对足够小的时间t,结合引理2.1,在时间段(0,t]内有下面4种情况

1)当保费收取和索赔发生次数都为0时,事件发生的概率为

Pr[N1(t)=0,N2(t)=0]=[1-λ1t+o(t)][1-λ2t+o(t)]=1-(λ1+λ2)t+o(t)

2)当保费收取0次,索赔发生k次时, 事件发生的概率为

Pr[N1(t)=0,N2(t)=k]=[1-λ1t+o(t)][αρkt+Ak(t)o(t)]=αρkt+Ak(t)o(t)

3)当保费收取1次,索赔发生0次时, 事件发生的概率为

Pr[N1(t)=1,N2(t)=0]=λ1t[1-λ2t+o(t)]=λ1t+o(t)

4)其它情况发生的概率为o(t)

对上述情况(2),当y>u+Fjt+σW(t)时,破产必然发生,此时V(u+Fjt+σW(t)-y;b)=0。利用全期望公式及盈余过程的马氏性,有

(3.1)

对于E[V(u+Fjt+σW(t);b)],由Taylor公式及布朗运动的性质得

(3.2)

又

(3.3)

(3.4)

把(3.2)-(3.4)式代入(3.1)式,化简得

上式两边同时除以t,且令t→0时有

定理3.2 当0≤u≤b时,红利付款现值的矩母函数M(u,z;b)满足的积分微分方程

当u>b时, M(u,z;b)=e(u-b)M(b,z;b)。

证明 当0≤u≤b时,类似定理3.1的方法,应用全期望公式

(3.5)

对于E[M(u+Fjt+σW(t),e-δtz;b)],由Taylor公式及布朗运动的性质得

故(3.5)式可表示为

进一步有

对上式两边同时除以t,且令t→0时有

定理3.3 当0≤u≤b时,红利付款现值的n阶矩Vn(u;b)满足的积分微分方程

证明 由定义1.4有

代入定理3.2,并比较zn的系数可得

[1] 张淑娜,陈红燕,胡亦钧.一类推广的复合Poisson-Geometric风险模型破产概率[J].数学志,2009,29(4):567-572.

[2] 耿金辉,李志民.保费再投资下COX风险模型的破产概率[J].贵州师范大学学报(自然科学版),2014,32(5):91-93.

[3] 侯致武,乔克林,张璐.一类风险模型赤字分布的函数型不等式[J].贵州师范大学学报(自然科学版),2015,33(4):72-74.

[4] 魏广华,高启兵,王晓谦.常利力下带干扰的双复合Poisson风险过程的生存概率[J].应用概率统计,2012,28(2):31-42.

[5] ZHANG Y Y,WANG W S.The perturbed compound Poisson risk model with constant interest[J].Chinese Journal of Applied Probability and Statistics,2015,31(4):375-383.

[6] HAO Y Y,YANG H.A ruin model with compound Poisson income and dependence between claim sizes and claim intervals[J].Acta Mathematicae Applicatae Sinica,English Series,2015,31(2):445-452.

[7] 乔克林,韩建勤.改进后的复合Poisson-Geometric风险模型的生存概率[J].重庆师范大学学报(自然科学版),2016,33(4):69-73.

[8] 韩建勤,乔克林.改进后的复合Poisson-Geometric风险模型的预警区问题[J/OL].重庆师范大学学报(自然科学版)[2016-01-13],http://www.cnki.net/kcms/detail/50.1165.N.20160713.1406.064.html.

[9] DE FINETTI B.Su un’impostazione alternativa dell teoria colletiva del rischio[J].Transactions of the XV International congress of Actuaries,1957,2:433-443.

[10]GERBER H U,SHIU E S W.on the time value of ruin[J].North American Actuarial Journal,1998,2(1):48-72.

[11]袁海丽,胡亦钧.带利率和常数红利边界的对偶风险模型的研究[J].数学学报(中文版),2012,55(1):131-140.

[12]赵金娥,何树红,王贵红.带线性红利和干扰的双复合Poisson风险模型[J].云南民族大学学报(自然科学版),2010,19(1):24-27.

[13]赵金娥,李明.双复合Poisson风险模型总红利现值的研究[J].西南大学学报(自然科学版),2015,37(1):104-109.

[14]赵金娥.常红利边界下带干扰的双复合Poisson风险模型[J].辽宁工程技术大学学报(自然科学版),2014,33(5):691-695.

[15]毛泽春,刘锦萼.索赔次数为复合Poisson-Geometric过程的风险模型及破产概率[J].应用数学学报,2005,28(3):419-428.

[16]汤珂.随机过程与金融衍生品[M].北京:中国人民大学出版社,2014.

Compound Poisson-Geometric risk model with a constant dividend and investment

QIAO Kelin,HAN Jianqin

(School of Mathematics and Computer Science,Yan’an University,Yan’an,Shaanxi 716000,China)

In this paper, the risk model whose the premium income followed the compound Poisson process and the claim numbers were a compound Poisson-Geometric process was considered with the constant dividend barrier strategy. Integral-differential equations with boundary conditions for the expectation, the moment generating function and nth moment of the discounted dividend payments until ruin were given by the method of total expectation formula and strong Markov property of the surplus process.

Poission process; Poission-Geometric process; constant dividend barrier; integral-differential equations

1004—5570(2016)06-0065-05

2016-05-28

陕西省教育厅专项科研计划项目(2013JK0576); 延安市科学技术研究发展计划项目(2014ZC-6);延安大学研究生教育创新计划项目(YCX201610)

乔克林(1964-),男,副教授,硕士,研究方向:金融数学及应用概率统计E-mail：yadxqklin@163.com.

O211.5

A