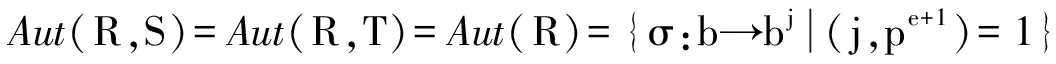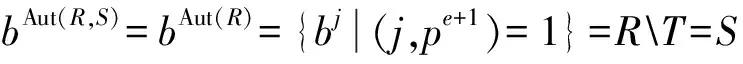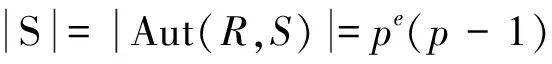完全多部图同构于一类循环群的Cayley齐次分解

张晓辉，温 玉，郝 英

(邯郸学院 数理学院，河北 邯郸 056002)



完全多部图同构于一类循环群的Cayley齐次分解

张晓辉，温 玉，郝 英

(邯郸学院 数理学院，河北 邯郸 056002)

设Γ=Ks[t]是一个完全多部图，R=Zn=〈a〉是一个循环群，其中n=st。令Τ=〈as〉≅Zt、S=RT，那么Γ=Ks[t]≅Cay(R,S)。构造出了多部图Γ同构于循环群的一类齐次分解，并对这种齐次分解进行了刻画。

完全多部图； 循环群； 齐次分解

定义1 设G是一个群，S为G的非空真子集，我们称如下定义的图为群G关于S的Cayley图：VΓ=G，且顶点u和v是连接的充要条件为uv-1∈S。这个Cayley图记为：Cay(G,S)。

定义2[1]设Γ是一个图，AΓ是图Γ的弧集。设= {P1,P2,…,Pk}(k≥2)是AΓ的一个分类，那么我们可以诱导出图Γ的一些子图Γi=(VΓ,Pi)。我们称Γi为图Γ的因子，而称Γ=Γ1+Γ2+…+Γk为图Γ的一个分解。当Γi两两同构时我们称该分解为图Γ的同构分解。

设Γ=Γ1+Γ2+…+Γk是图Γ的一个同构分解。由于Γi=(VΓ,Pi)两两同构，所以Γi=

定义3[2]假设={P1,P2,…,Pk}是弧集AΓ的一个分解(k≥2)，M

(i)M在顶点集VΓ上是传递的，并且M稳定每个集合Pi。

定义4 如果M在顶点VΓ上是正则的，并且M◁G，这时称定义2中的齐次分解为M-Cayley齐次分解。此时，由诱导的子图Γi叫做M-Cayley图。

定义5 由单个的n阶元素a生成的群称为循环群，记作Zn=〈a〉。

引理2 设群G传递作用于非空集合Ω上，H◁G且H在Ω上不传递，则H在Ω上半传递。

引理3[3]设Γ=Cay(R,S)是一个Cayley图，H是Aut(R,S)的一个子群且H在S上半传递，则图Γ存在一个各因子度数均相等的分解。

任取Pi∈。由于(yg)(xg)-1= yx-1∈Si，我们有。又因为H保持Si不变，所以，即保持每个Pi不变。

任取Pi∈，则yx-1∈Si。因为L在传递，所以存在Si∈，使得(yg)l((xg)l)-1=(ygg-1x-1)l=(yx-1)l∈Sj，由已知在VΓ上传递，进而。又因为，所以，即保持={P1,P2,…,Pk}不变。

任取Pi,Pj∈、(x,y)∈Pi，则yx-1∈Si。因为L在上传递，故存在g∈L，使得yg(xg)-1=(yx-1)g∈Sj，进而(x,y)g=(xg,yg)∈Pj。又因为，所以，即L在上传递。进一步，由于，我们有G也在传递。

引理5 设R=〈a〉是一个循环群，其中 ° (a)=n=st。令T=〈as〉、S=RT，则Aut(R,S)=Aut(R,T)=Aut(R)。

证明 ∀σ∈Aut(R,S)，则Sσ=S，即(RT)σ=RT，进而Tσ=T。所以我们有

=Aut(R,T)

该引理的前半部分得证。

所以我们有〈as〉=〈ais〉=〈(as)δ〉=〈as〉δ，即Tδ=T，进而Aut(R)⊆Aut(R,T)。又因为Aut(R,T)⊆AutR，所以Aut(R,T)=AutR。证毕。

现在我们按照引理4提供的方法来构造图Γ=Ks[t]≅Cay(R,S)(R为循环群)的齐次分解，并对具备这种齐次分解的图进行刻画。对此我们有下面的定理成立。

定理1 图Γ=Ks[t]≅Cay(R,S) (R为循环群)具有引理4所提供的齐次分解，当且仅当s=t,t=pe，其中p是一个素数。

反之，设Γ=Kp[pe]是一个完全多部图，其中p是一个素数。令R=Zpe+1=〈b〉、T=〈bp〉≅Zpe、S=RT，那么Γ=Kp[pe]≅Cay(R,S)。显然b∈S，又因为

所以：

[1] GIUDICI M,LI C H,POTOCNIK P,et al.Homogeneous factorisations of graph products[J].Discrete Math,2008,308:3652-3667.

[2] 张晓辉，卢建岳，李根亮，等.完全图的循环齐次分解[J].云南大学学报(自然科学版),2010,32(3):254-257.

[3] LI C H,GIUDICI M,PRAEGER C E.Homogeneous factorizations of complete graphs with edge-transitive factors[J].Algebraic Combin,2009,29:107-132.

[4] LI C H,PRAEGER C E.Homogeneous factorisations of complete multipartite graphs[J].Discrete Math,2007,307:415-431.

[5]LI C H.On isomorphisms of finite Cayley graphs-asurvey[J].Discrete Mathematics,2002,256:301-334.

[6] 徐明曜.有限群导引(上,下册)[M].北京：科学出版社,1999.

[7] 张远达.有限群构造[M].北京：科学出版社,1982.

Cayley homogeneous factorization of complete multipartite graphs isomorphic to cyclic group

ZHANG Xiaohui,WEN Yu,HAO Ying

(Department of Mathematics,Handan College,Handan, Hebei 056002,China)

Let Γ=Ks[t]be a complete multipartite graphs, R=Zn=〈a〉 is a cyclic group, n=st. Let Τ=〈as〉≅Zt、S=RT, that Γ=Ks[t]≅Cay(R,S).we can characterize a class of homogeneous factorization of the complete multipartite graphs Γisomorphism to cyclic group.

complete multipartite graphs;cyclic group;homogeneous factorization

1004—5570(2016)06-0050-02

2016-06-20

河北省社科基金(201603040127)

张晓辉(1982-)，女，河北人，讲师，研究方向：群与图方面，E-mail: nizi112@126.com.

O175

A