率失真优化的压缩感知图像编码

蒋 伟，杨俊杰

(上海电力学院 电子与信息工程学院，上海 200090)



率失真优化的压缩感知图像编码

蒋 伟，杨俊杰

(上海电力学院 电子与信息工程学院，上海 200090)

针对基于压缩感知的图像编码系统，分析了系统中编码参数和码率以及失真的关系，在此基础上提出了基于压缩感知的图像编码系统的码率-失真模型。根据所提模型设计了率失真优化的压缩感知图像编码算法。在给定码率的条件下，优化编码参数，使得编码器失真最小。算法在Matlab的编码平台上进行了仿真和实验，结果证明提出的码率-失真模型能够很好地拟合实际率失真曲线，并且基于该模型的率失真优化算法有效的提高了压缩感知图像编码系统的性能。

压缩感知；率失真；编码

2006年Donoho and Candes首次提出了压缩感知的理论[1-2]。该理论是一种将高维空间的信号转换为低维信号的采样方法。如果输入信号足够的稀疏，那么这个信号就可以很高的精度被重构。基于压缩感知的图像编码框架摒弃了传统的先采样后处理的级联结构，将采样和数据压缩结合起来，简化了编码框架[3-4]。通过使用压缩感知降低了编码器的复杂度，而解码端由于需要求解凸优化的问题来恢复输入信号，因而复杂度较高，所以基于压缩感知的图像编码系统适合于能量受限的编码场合，如传感器网络。

率失真性能是衡量图像编码系统性能的重要准则。率失真技术可以不受编码结构和技术的限制，通过配置最优的编码参数提高编码性能，是实际编码系统中常用的优化方法。量化是传统的有损编码系统中的主要失真来源，量化器性能很大程度上决定了编码效率，因而可以选择合适的量化参数使得给定编码码率下失真最小。然而在基于压缩感知的图像编码系统中除了量化，采样过程也会引起失真和码率的变化，也就是说给定码率条件下最优的编码性能由量化参数和采样参数共同决定。因而分析量化参数、采样参数和编码码率、失真之间的关系对确定最优的参数配置至关重要。

目前在基于压缩感知的图像编码系统的编码参数和码率失真之间关系的研究方面已有一些成果。文献[5]中针对传统的视频编码系统提出了延迟-能量-率失真模型。文献[6-7]针对压缩感知编码视频流提出了码率-能量-失真模型。该模型可以用于估计接收端接收到的受信道噪声污染的视频流的质量。但在基于压缩感知的图像编码系统中最优的编码参数选择方面研究成果较少。文献[8]中针对分布式视频压缩感知编码框架提出了压缩感知采样率的分配方法，该方法基于图像区域的稀疏程度进行采样率的分配，稀疏度高的区域分配较低的采样率，稀疏度低的区域分配较高的采样率。但是该方法并没有考虑量化对编码码率和失真的影响。而且算法还需要额外传输附加信息到接收端。文献[9]提出了率失真优化的码率分配方案，然而算法的效率很大程度上取决于失真模型的正确性。

本文首先分析了基于压缩感知的图像编码系统的编码参数与码率和失真之间的关系，然后分别提出了码率和失真模型，最后将上述模型用于压缩感知编码算法的优化，提出了基于率失真优化的压缩感知编码算法，选择最优的采样率和量化参数，使得编码器性能最佳。

1 压缩感知

压缩感知(Compressive Sensing)是通过线性投影将高维信号编码为低维信号的采样方法。压缩感知包括3个主要问题：稀疏表示、信号测量和信号重构。压缩感知理论实现的基础是信号的稀疏性。稀疏度定义为离散时间信号中非零元素的个数。如果在某个正交基下信号是稀疏的，并且稀疏度K远小于信号的维数N，那么该信号被称为稀疏的或可压缩的，可以通过压缩感知对信号压缩。自然图像在诸如离散余弦变换和小波变换这类变换下都是稀疏的，因此将图像看作矢量u∈RN，那么图像在正交基ΨN×N下的映射信号x是

x=Ψu

(1)

假设存在测量矩阵Φ，维数是L×N，L≤N，则通过非相关测量将信号x投影到测量矩阵Φ上，即

y=Φx=ΦΨu

(2)

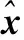
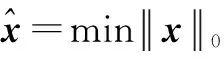
(3)

由于L≤N，式(3)的求解是一个病态问题，有无穷多组解，计算复杂度很高。因此Donoho and Candes提出当满足RIP条件时，可以用l1范式代替l0范式，将式(3)转换为一个凸优化问题进行求解

(4)

通常采样个数L≥αKlogN时，可以精确重构出x。其中α是一个很小的常数。在实际环境中通常存在各种各样的噪声，对测量数据造成干扰，比如图像压缩系统中编码端就会引入量化误差。在噪声环境下信号的重构可以进一步写为

(5)

其中:参数ε表示噪声。在重构过程中，重构信号质量与测量矩阵、正交基都有关系。精确重构原信号所需的样本个数也由正交基和测量矩阵的相关性决定[12]。正交基和测量矩阵的相关性越低，精确重建稀疏信号所需要的采样个数就越少。

2 码率-失真模型

传统的视频编码系统中，量化是产生失真的主要原因，量化参数(量化步长)越大，失真越大，编码码率越小；而在压缩感知编码系统中，失真由量化和线性测量共同产生。量化参数和测量数目的设置直接影响系统的性能。比如减小量化步长会提高码率，减小失真；而增大量化步长会降低码率，增加失真。增加采样个数会增加码率，同时减小失真；而减小测量数目会降低码率，增加失真。由于无法保证码率和失真同时达到最小，因此需要在码率和失真这两个参数中获取最优的Pareto均衡。

采样个数和量化参数互不相关，因此可以分别分析他们对码率和失真的影响。当测量值的数目固定时，码率和失真随量化参数的变化如图1和图2所示。图中，Rcs表示采样个数占总数的百分比，失真是源图像和重构图像之间的均方误差。可以看出采样个数不变时，码率随着量化参数的增大而下降，失真随量化参数的增大而增加。从图1a和图2a中可以看出，码率和量化参数QP之间近似服从幂函数的分布，而图1b和图2b中失真和量化参数也近似服从幂函数分布，码率和失真与量化阶之间的关系可表示为

R1=α1·QPα2

(6)

D1=α3·R1α4

(7)

式中：α1，α2，α3和α4是模型参数，取值与原信号有关；R1表示码率；D1表示失真。 当量化参数固定时，码率和失真随采样个数变化如图3和图4所示。可以看出码率R2随采样个数呈线性变化，失真D2随采样个数呈指数分布

R2=β1·NCS

(8)

D2=β2·eβ3R2

(9)

式中：β1，β2，β3是模型参数，因此可以建立码率R和采样个数NCS、量化参数QP之间的数学模型

R=aR·NCSβR·QpγR

(10)

式中：αR，βR和γR是模型参数，取值与原信号有关。总失真由测量模块产生的失真和量化模块产生的失真构成，D=D1+D2。测量模块产生的失真随采样个数呈指数分布，量化产生的失真服从幂函数分布，因此失真模型可以定义为

D=αD·RβD+γD·eθDR

(11)

式中：αD，βD和γD是模型参数，取值与原信号有关。

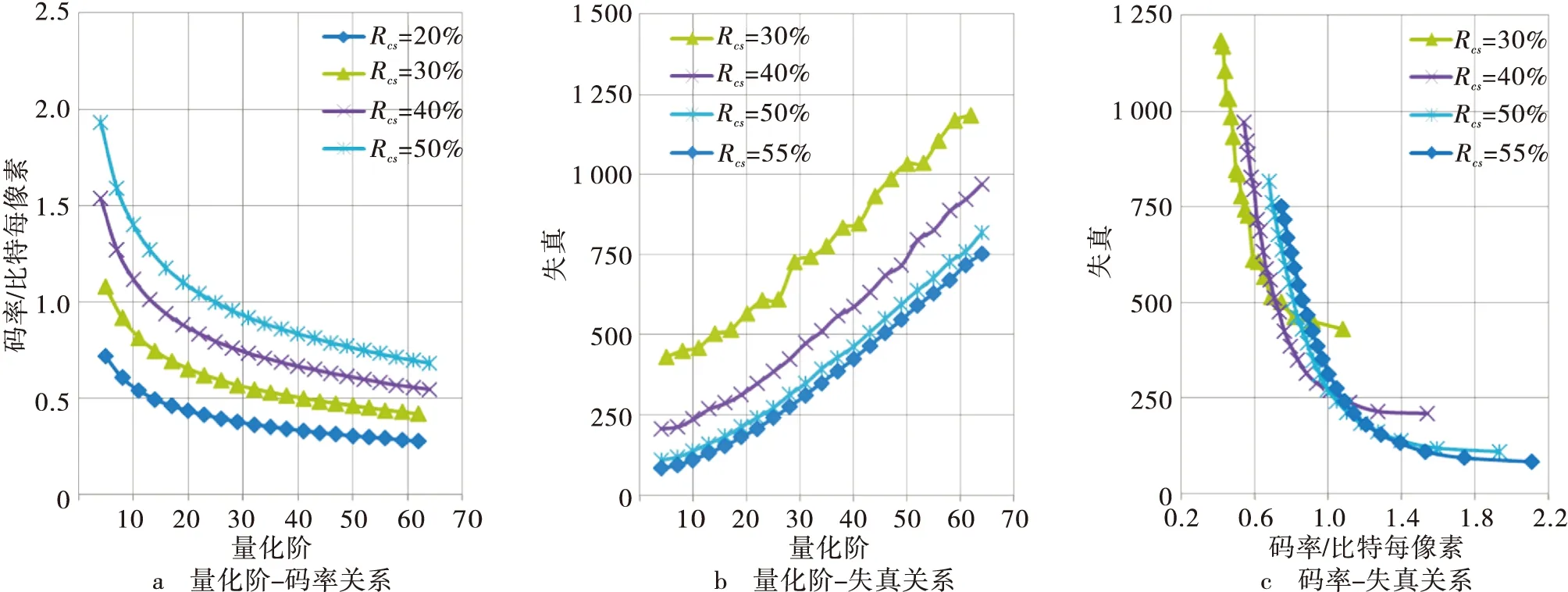
图1 测量值个数固定时码率失真关系，Lena

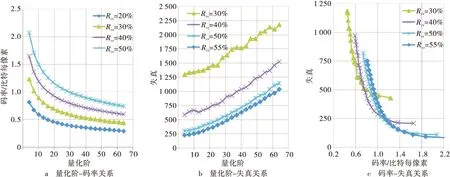
图2 测量值个数固定时码率失真关系，Bank

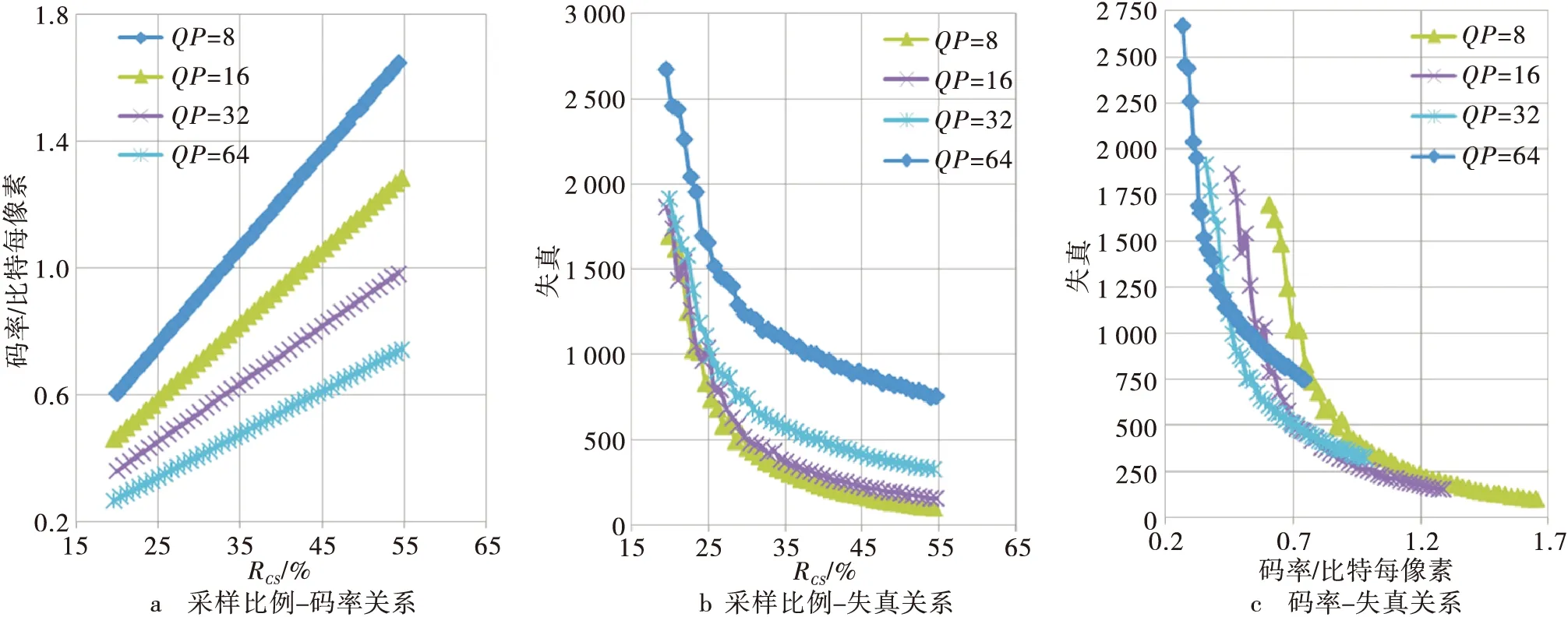
图3 量化参数固定时码率失真关系，Lena

图4 量化参数固定时码率失真关系，Bank

3 率失真优化的压缩感知编码

理想情况下期望最优的编码器以最小的码率获得失真最小的图像，也就是在给定码率Rb的条件下失真最小的编码器

minD(U,S) s.t.R(U,S)≤Rb

(12)

式中：U是源图像；S是编码器配置参数矢量；D(U，S)，R(U，S)分别是失真和码率。式(12)的最优值就是码率受限条件下最优的视频编码器性能。从式(12)中可以看出，编码器的失真受码率的约束，无法同时使得码率和失真最小。当给定编码码率一定时，如果分配较多比特用于采样，那么用于表示每个样值的比特数较少，导致失真增大；反之，如果用于量化的比特数较多，那么用于采样的比特就会较少，同样导致失真增大。因此根据上节提出的码率-失真模型，分析码率、失真和编码参数(量化参数和采样个数)之间的关系，提出了基于率失真优化的压缩感知编码算法，求解最优的编码参数配置，得到给定码率条件下的失真最小的编码器。

压缩感知编码框架中影响性能的因素有2个，即采样个数和量化参数，因此最优的编码参数配置实际上就是求解能够使编码效率最高的采样个数和量化参数。式(12)可以改写为

minD(U,NCS,QP) s.t.R(U,NCS,QP)≤Rb

(13)

式中：D(U,NCS,QP)和R(U,NCS,QP)分别是在编码参数NCS,QP下得到的失真和码率。通过式(10)的码率模型可以计算出每组NCS,QP的取值下对应的编码码率，通过式(11)可以得到在该码率下产生的失真。式(13)可以使用拉格朗日法或是动态规划法求解。由于动态规划的复杂度随着编码单元的增加呈指数上升，导致计算量巨大，因此通常采用拉格朗日法求解。当满足KKT条件时，式(13)表示的受限优化问题可以转换成不受限优化问题，可以由下式解出

minJ(U,NCS,QP,λ)=D(U,NCS,QP)+

λR(U,NCS,QP)

(14)

式中：λ≥0称为拉格朗日因子，也是率失真曲线的斜率。λ用来衡量码率和失真的相对重要性。λ越小失真越重要，λ越大码率越重要。拉格朗日代价值J(U,NCS,QP,λ)用于衡量编码性能的优劣，代价值越小编码性能越好。能够使得代价值最小的参数配置S*={N*CS,Q*P}就被称为最优的参数配置，对应的λ*是最优的率失真斜率，失真D*是在该码率Rb下的最小失真。诸如牛顿法或二分法这类快速搜索算法通常用于求解λ*，然而算法复杂度都较高，相当耗时。本文中通过求解KKT条件计算最优的拉格朗日因子。既然最优的参数配置S*使得J(U,NCS,QP,λ)达到最小值，那么J(U,NCS,QP,λ)的梯度在S*的值为0，也就是

(15)

R(S*)≤Rb

(16)

λ*≥0，λ*(R(S*)-Rb)=0

(17)

(18)

因此如果存在λ*满足KKT条件，对应的S*也就是J(U,NCS,QP)的最小值。求解满足KKT条件的λ*就可以得到式(14)的最优解，也就是最优的压缩感知编码器。

4 实验结果

本文所提算法基于Matlab编码平台进行了实验。在发送端待测图片先进行小波变换，得到稀疏信号，然后由测量矩阵进行采样，采样后的数据再经过均匀量化和算术编码生成编码码字。在接收端编码码字先算术解码和反量化，然后根据得到的采样数据进行重构。目前有多种重构算法，算法的性能与图片在小波域的稀疏性有关。本实验中采用OMP(Orthogonal Matching Pursuit)算法重构信号[13]。重构后的信号再经过小波反变换就恢复出了原图片。

实验测试了文中所提的码率和失真模型的正确性。图5显示了根据码率模型估算的码率和实际测试码率的比较。从图中可以看出，由采样数目和量化参数估算的码率和实际编码码率相符。依据码率-失真模型计算出的率失真曲线和实际测试曲线的对比如图6所示。其中图6a是在固定量化参数条件下得到的率失真曲线，图6b是在固定测量数目的条件下得到的率失真曲线，并且图中的曲线代表实际测试得到的率失真关系，菱形和星型代表模型计算结果。从图中可以看出模型产生的率失真曲线和实际曲线相符。实验还对率失真优化的压缩感知编码系统的性能进行了测试。测试结果如图7所示。可以看出根据本文提出的码率-失真模型对编码系统进行率失真优化后，系统的编码性能有了明显提高，和未优化时相比增益约有2 dB。

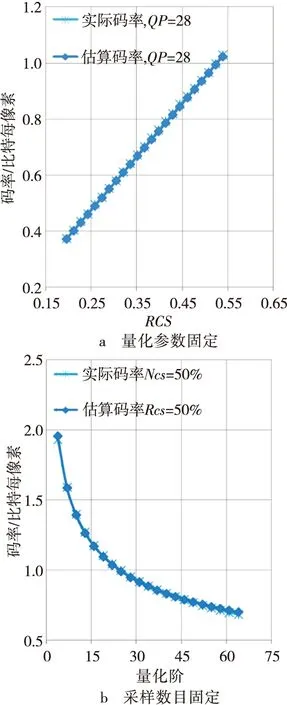
图5 码率和编码参数的关系，Lena

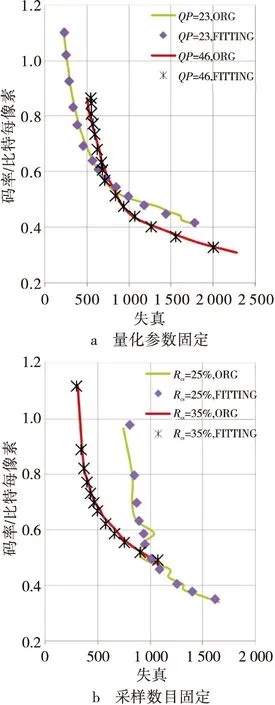
图6 码率-失真模型曲线，Lena

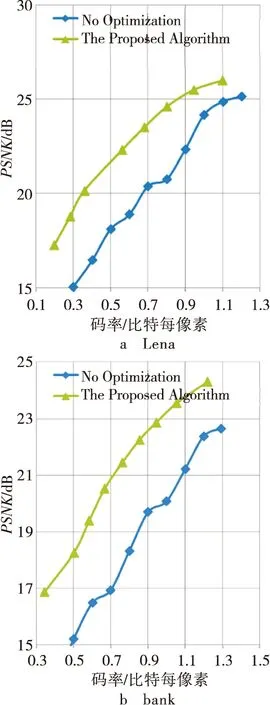
图7 率失真优化的压缩感知编码性能

5 结论

本文通过分析压缩感知编码系统中编码参数和码率以及失真的关系，提出了基于压缩感知的图像编码系统的码率-失真模型。并且根据所提模型设计了率失真优化的压缩感知图像编码算法。通过优化测量数目和量化参数，得到给定码率下失真最小的编码器。实验结果表明该码率-失真模型能够很好地拟合实际率失真曲线，以此为基础提出的率失真优化算法能够有效提高压缩感知图像编码系统的性能。

[1]DONOHO D. Compressive sensing[J]. IEEE transactions on information theory，2006，52(4)：1289-1306.

[2]CAND`ES E.，ROMBERG J，TAO T. Robust uncertainty principles，EXACT signal reconstruction from highly incomplete frequency information[J].IEEE transactions information theory，2006，52(2)：489-509.

[3]左觅文，常侃，施静兰，等. 一种自适应采样率视频压缩感知方案[J].电视技术，2015，39(2)：66-70.

[4]覃远年，徐晓宁．立体视频图像编码的研究进展[J].电视技术，2015，39(7)：10-14.

[5]WU X L，ZHANG X J. Model-guided adaptive recovery of compressive sensing[C]// Proc. Data Compression Conf(DCC).UT，USA：IEEE ，2009：123-132.

[6]GOYAL V K，FLETCHER A K，RANGAN S. Compressive sensing and lossy compression[J].IEEE signal processing magazine，2008，25(2)：48-52.

[7]WU S H，PENG W H，CHIANG T. Bit-plane compressive sensing with bayesian decoding for lossy compression[C]//Proc. 28th Picture Coding Symposium.Nagoya，Japan：IEEE，2010：606-609.

[8]LI C L，WU D P.Delay-power-rate-distortion model for wireless video communication under delay and energy constraints[J].IEEE transactions on CSVT，2014，24(7)：1170-1183.

[9]PUDLEWSKI S，MELODIA T. A rate-energy-distortion analysis for compressed-sensing-enabled wireless video streaming on multimedia sensors[C]// IEEE Globecom.Texas，USA：IEEE，2011：1-6.

[10]CANDES E，WAKIN M. An introduction to compressive sampling[J].IEEE signal processing magazine，2008，25(2)：21-30.

[11]魏从静，唐加山．基于行列式随机循环的压缩感知测量矩阵研究[J]. 电视技术，2015，39(19)：6-10．

[12]DO T T，GAN L，NGUYEN N，et al. Sparsity adaptive matching pursuit algorithm for practical compressed sensing[C]// Asilomar Conference on Signals，System and Computer.Pacific Grove，CA：IEEE，2008：581-587.

[13]郎利影，王勇，李思骞.基于压缩感知OMP改进算法的图像重构[J]. 电视技术，2015，39(6)：8-12.

蒋 伟(1975— )，女，副教授，主要研究方向为图像压缩；

杨俊杰(1977— )，教授，主要研究方向为电力通信技术、光纤通信技术等。

责任编辑：许 盈

Rate-distortion optimized compressive sensing based coding

JIANG Wei, YANG Junjie

(SchoolofElectronicsandInformationEngineering,ShanghaiUniversityofElectricPower,Shanghai200090,China)

In view of compressive sensing based image coding schemes, the relationship of rate and coding parameters and relationship of distortion and coding parameters are analyzed. Moreover, a source rate and distortion model is proposed. Based on the R-D model, the optimal number of measurements and quantization step size are determined according to the rate-distortion criteria. The proposed algorithm is implemented on the platform of Matlab. The accuracy of the proposed R-D model is verified through experiments. Experimental results show that the proposed algorithm improves coding performances substantially.

compressive sensing; rate-distortion; coding

蒋伟，杨俊杰. 率失真优化的压缩感知图像编码[J].电视技术，2016，40(11)：12-17. JIANG W，YANG J J. Rate-distortion optimized compressive sensing based coding[J].Video engineering，2016，40(11)：12-17.

TN915

A

10.16280/j.videoe.2016.11.003

国家自然科学基金项目(61401269；61371125)；上海市自然科学基金项目(14ZR1417400)；地方能力建设项目(14110500900；15110500900)

2016-06-24