木质粉末热模压成形致密化过程数值模拟
董俊辉,刘克非,陈 飞,吴庆定
(中南林业科技大学 工程流变学湖南省重点实验室,湖南 长沙 410004)
木质粉末热模压成形致密化过程数值模拟
董俊辉,刘克非,陈 飞,吴庆定
(中南林业科技大学 工程流变学湖南省重点实验室,湖南 长沙 410004)
为探寻木质粉末热压成形致密化规律,基于杨木粉末与芦苇粉末热压成形实验数据,借助有限元法分析成形压力对其压坯密度的影响,并通过理论计算与实验验证相结合的方法对成形压力与压坯密度的关系进行回归分析。结果表明:在热压工艺条件下,依据Shima模型的计算数据与实验结果存在明显偏差,但当成形压力不小于50 MPa时,通过理论计算、实验检测与分析修正获得的由理论方程与修正项组成的杨木粉末和芦苇粉末的热压成形“压力-密度”模型与实验结果高度吻合。
木质粉末;热压成形;致密化;数值模拟
虽说国内外有关粉末材料模压致密化过程数值模拟研究的报道很多,但基于木质粉末相关研究的公开报道并不多见[1-4]。尽管已有的研究成果基于粉末材料“可压缩连续体”的理想假设,建立了一系列的理论与准则,如:Kuhn等学者提出的多孔介质材料模型[5]、Shima材料模型[6]、Doraivelu准则[7]、Kim准则[8]等;遗憾的是,由于非连续介质力学基础的不完善,使得这些理论与准则在工程上的应用受到了很大限制。本文试图基于粉体材料连续性假设,应用Shima模型运用MSC.MACR有限元分析软件,以白杨粉末和芦苇粉末为例,在室温模压致密化过程模拟分析结果[1]的基础上对木质粉末热模压致密化过程进行模拟分析,从而建立木质粉末热模压致密化过程的数值模型,以缩短人工木质新材料的开发周期,减少试验工作量和研发成本,并进一步优化木质粉末热模压成形工艺。
1 木质粉末冷压成形过程数值模拟
分析发现[2],木质粉末的松装密度随粒度的变化不大,约为绝干密度的1/2;其粒度组成呈正态分布,与金属粉末的粒度分布类似;其颗粒排列无序、形状各异、多为长条状;其模压成形过程是一个典型的非线性弹塑性接触问题。
有限元分析软件MARC[9]对于非线性热弹塑性问题具有强大的有限元分析和计算能力,笔者利用该软件以白杨粉末和芦苇粉末为例对木质粉末的模压成形致密化过程进行了数值模拟。模拟结果表明,在弹塑性理论的理想假设下,Shima模型可对木质粉末的冷模压致密化过程进行很好的模拟。试验结果与理论模型计算数据高度吻合(如图1所示),说明木质粉末在室温环境下模压致密化行为与金属粉末类似[1-2]。
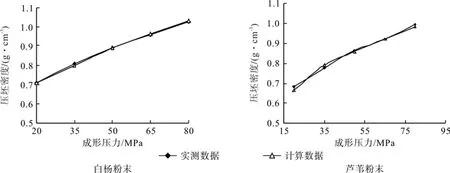
图1 木质粉末密度-压力曲线Fig.1 Wood powder density - pressure curve
2 木质粉末热压成形过程数值模拟
2.1 温度场有限元模型的建立
木质粉末热模压成形工艺已趋成熟[2-4],据此可建立如图2所示的有限元模型。将网格划分为10×15,采用8节点单元,计算规模为1 200节点,单元类型为热传导单元,单元号42。在边界上施加160℃的温度载荷后进行对流分析。
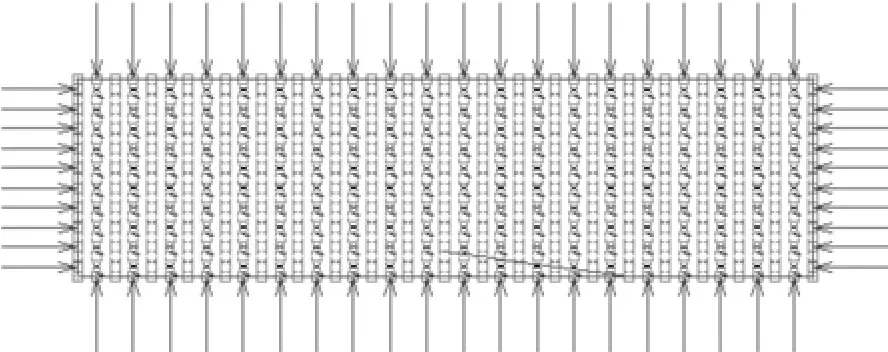
图2 热传导有限元模型Fig.2 The fi nite element model of heat conduction
2.2 温度场分布
图3为木质粉末在9MPa×160℃条件下保温保压30 s时的温度场分布图(取导热系数0.12 W/mk、导温系数0.0014e-4 m2/s)。
很明显,加载温度后,压坯表层温度明显高于内部温度,温度场从外到里呈梯度分布。另外,由于粉末体局部粒度分布、含水率等的差异,温度场的实际分布也会有差异。
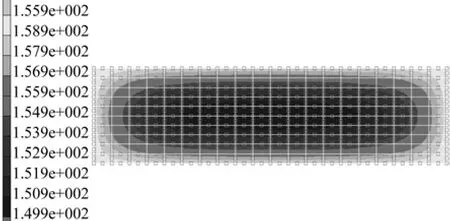
图3 木粉压坯温度分布云图Fig.3 Temperature distribution nephogram of wood powder compact
2.3 密度-压力有限元模型
为相互印证计算结果,在有限元模型中对白杨粉末和芦苇粉末采用了不同的计算起始位置。白杨粉末的计算起始点:20 MPa、13.39 mm(有限元网格如图4 a);芦苇粉末的计算起始点:0 MPa、69.93 mm(有限元网格如图4b)。变化参照点:白杨粉末,20 MPa、13.39 mm(高度变化量为28.75);芦苇粉末,20 MPa、12.42 mm。试验压力:20 MPa、35 MPa、50 MPa、65 MPa、80 MPa,在160℃成形温度下各保压30min,测量5个点的试验数据。
2.4 密度-压力数值模拟
图5~图7分别为20 MPa、50 MPa、80 MPa压制压力下,白杨粉末和芦苇粉末压坯内部相对密度随成形压力的变化分布图。
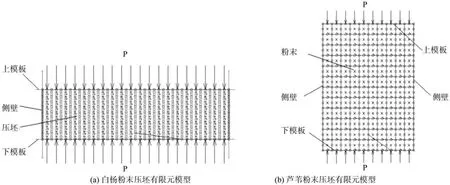
图4 “密度-压力”有限元模型Fig.4 Finite element model of density - pressure
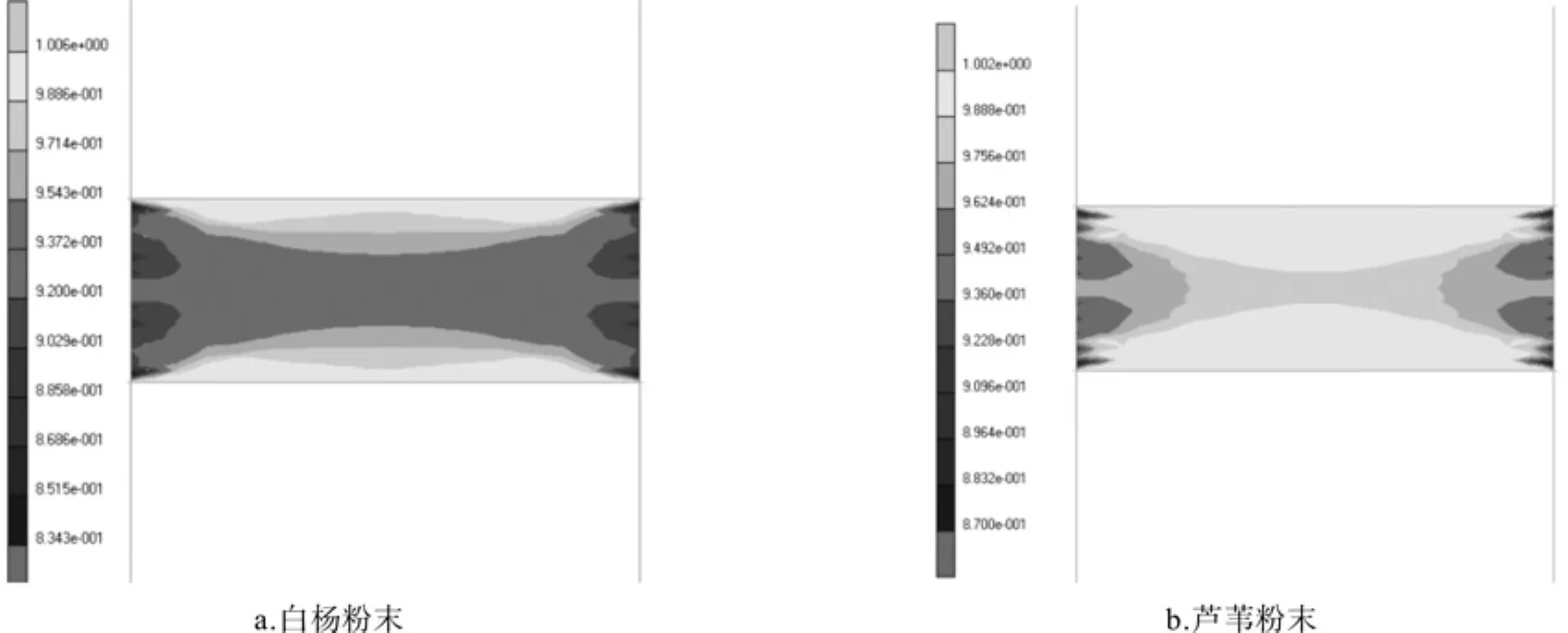
图5 20 MPa时压坯内部相对密度分布图Fig.5 Relative density distribution in inner compact at 20 MPa

图6 50 MPa时压坯内部相对密度分布图Fig.6 Relative density distribution in inner compact at 50 MPa
图5~图7表明,热模压成形过程中白杨粉末和芦苇粉末的压坯内部密度分布不均匀,说明压坯与成形模型腔侧壁之间的摩擦力对压坯内部应力产生了显著影响;且随着成形过程的延续与成形压力的增大,压坯内部密度差异逐步减小。
由于成形模的刚性约束,粉末压坯在热成形阶段的截面积保持不变,而厚度发生不同程度的变化,图8~图10为白杨粉末和芦苇粉末压坯在20 MPa、50 MPa、和80 MPa成形压力下时厚度变化图,据此可根据公式(1)计算出不同热成形压力下的压坯密度,进而绘制出白杨粉末和芦苇粉末热压成形压坯的“密度-压力”曲线(示于图11)。

图7 80 MPa时压坯内部相对密度分布图Fig.7 Relative density distribution in inner compact at 80 MPa

图8 20 MPa时的压坯厚度变化绝对值Fig.8 Thickness change absolute value of compact at 20 MPa

图9 50 MPa时的板坯高度变化绝对值Fig.9 Thickness change absolute value of compact at 50 MPa

式中,ρ0:初装密度;h0:初装高度;Δh:高度变化绝对值。
从图11不难看出,通过有限元法计算得出的木质粉末热压压坯的密度数据与实测数据存在明显差异。
2.5 差异分析
上述有限元模型的建立是基于白杨粉末、芦苇粉末等木质粉末颗粒体积不变的理想假设。而白杨粉末、芦苇粉末这类木质材料由半纤维素、纤维素和木质素等部分结晶体组成[2,10],当加热到玻璃化温度时,粉末材料的结晶区会由玻璃态向橡胶态转化,此时粉末材料的物理力学性能会发生显著变化,如强度急剧下降、蠕变显著增加,由此造成了压坯密度计算曲线与实测曲线的明显偏差(正如图11所示结果)。此外,含水率等因素对木质粉末热压成形过程的“密度-压力”曲线均有影响。
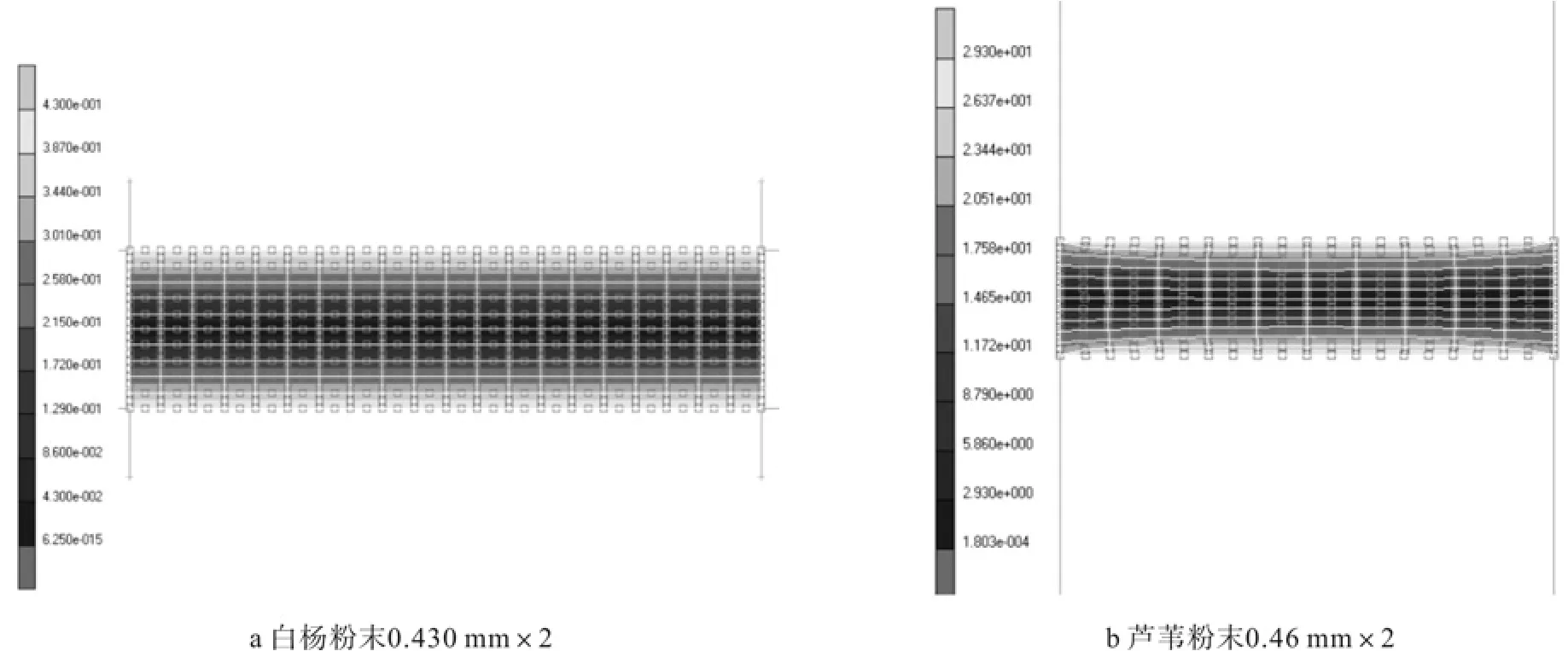
图10 80 MPa时的板坯高度绝对变化值Fig.10 Thickness change absolute value of compact at 80 MPa
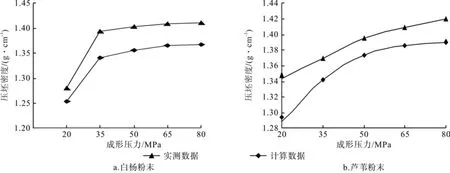
图11 “密度-压力”曲线Fig.11 density - pressure curve

表1 杨木粉末热压成形“压力-密度”方程计算数据表Table 1 Pressure-density equation calculation data of thermoforming of poplar powders
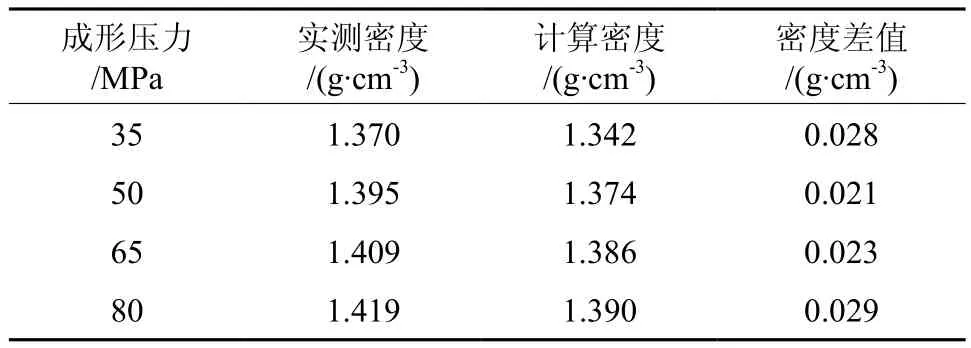
表2 芦苇粉末热压成形“压力-密度”方程计算数据表Table 2 Pressure-density equation calculation data of thermoforming of reed powders
2.6 “压力-密度”数学模型
利用统计分析软件SPSS Statistics[11-12],基于图11对应的理论计算与试验分析数据建立“压力-密度”理论方程和修正方程。
2.6.1 压力-密度理论方程
由图11数据可得白杨与芦苇粉末在160℃/30min热压条件下的压力-密度方程计算数据,列于表1、表2。据此,通过回归分析,可建立杨木粉末与芦苇粉末的“压力-密度”理论方程。
(1)杨木粉末的热压成形“压力-密度”理论方程
成形压力为20~50 MPa时,杨木粉末热压成形“压力-密度”理论方程回归分析模型汇总与参数估计见表3由此可得回归方程:
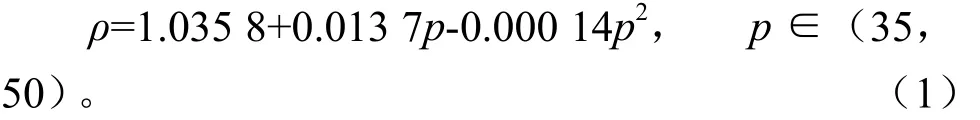
式中,ρ:压坯密度,g/cm3;p:成形压力,MPa。

表3 压力为20~50 MPa时的模型汇总和参数估计值†Table 3 Model summary and parameter estimation value at pressure of 20 to 50 MPa
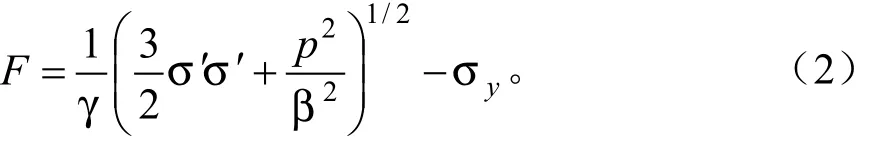
式中:F为屈服强度,MPa;σy为单向屈服应力,MPa;下标y表示流动应力的方向;σ′为偏应力分量张量,MPa;P为静水压力,MPa;γ、β为材料参数,均为相对密度的函数。
成形压力为50~80 MPa时,杨木粉末热压成形“压力-密度”理论方程回归分析模型汇总与参数估计值见表4由此可得回归方程:
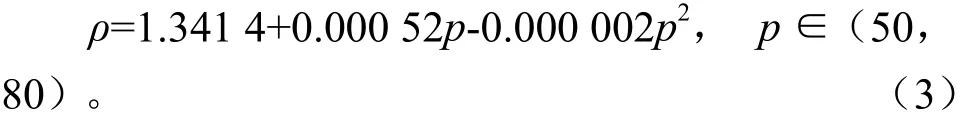
式中,ρ:压坯密度,g/cm3;p:成形压力,MPa。

表4 压力为50~80 MPa时的模型汇总和参数估计值†Table 4 Model summary and parameter estimation value at pressure of 50 to 80 MPa

表5 压力为20~50 MPa时的模型汇总和参数估计值†Table 5 Model summary and parameter estimation value at pressure from 20 to 50 MPa
(2)芦苇粉末的热压成形“压力-密度”理论方程
成形压力为20~50 MPa时,芦苇粉末热压成形“压力-密度”理论方程回归分析模型汇总与参数估计见表5由此可得回归方程:
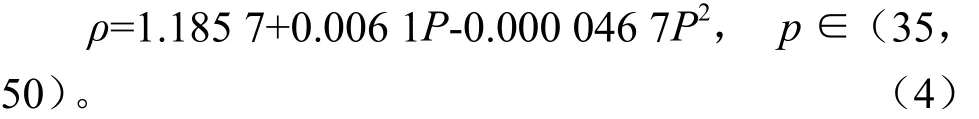
式中,ρ:压坯密度,g/cm3;P:成形压力,MPa。
成形压力为50~80 MPa时,芦苇粉末热压成形“压力-密度”理论方程回归分析模型汇总与参数估计见表6由此可得回归方程:


表6 压力为50~80 MPa时的模型汇总和参数估计值†Table 6 Model summary and parameter estimation value at pressure of 50 to 80 MPa
式中,ρ:压坯密度,g/cm3;P:成形压力,MPa。
由上述回归方程可得,杨木粉末和芦苇粉末热压成形过程的“压力-密度”通用理论方程为:
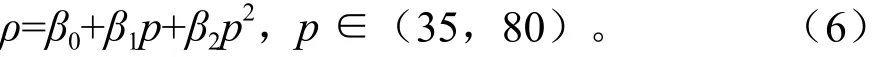
式中,ρ:压坯密度,g/cm3;p:成形压力,MPa;β0、β1、β2:通过有限元法计算所得特定材料的理论方程系数。
2.6.2 压力-密度修正方程
根据表1,采用压力为35~50 MPa时的模型,用统计分析软件SPSS以杨木粉末热压成形压坯的计算密度和实测密度差异为因变量、成形压力为自变量进行线性回归分析。结果显示:所取回归分析数据均被采入,模型的剔除变量为因变量密度差,导入变量为自变量压力;相关系数R=0.772,判定系数R2=0.596,校正系数为0.394,标准差为0.004 555,表明回归数据具有明显的线性关系。由方差分析表(表7)和回归系数分析表(表8)可以看出:回归系数为0,回归系数检验统计量t<α,说明此时成形压力对压坯密度差的影响不明显;非标准回归系数βn=0.059,t<α,说明常数项对密度差有影响。
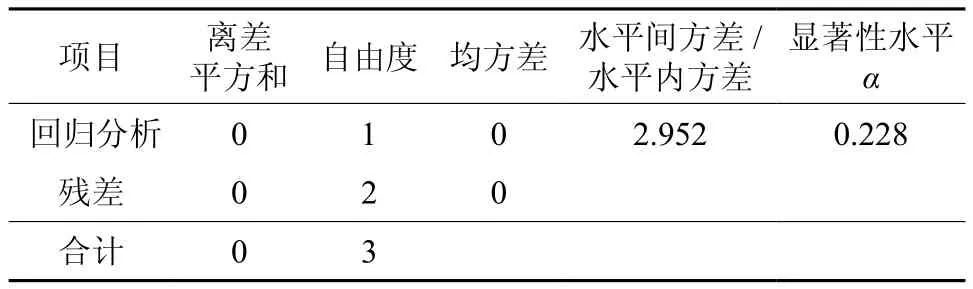
表7 方差分析†Table 7 Variance analysis
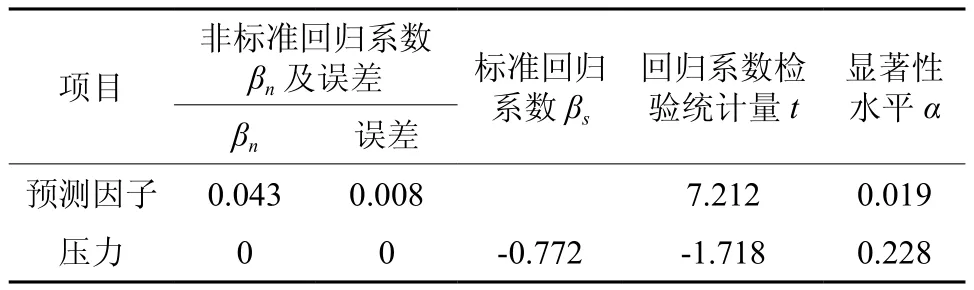
表8 回归系数分析表†Table 8 Regression coefficient analytic statement
可得杨木粉末热压成形“压力-密度”回归修正方程:

式中:Δρ为压坯密度修正值,g/cm3;p为成形压力,MPa。
上述分析表明:当成形压力不小于50 MPa时,压坯密度的变化与成形压力关系不大,压力-密度通用修正方程退化为常数Δ。
同样方法可求得芦苇粉末热压成形“压力-密度回归修正方程”:

式中:Δρ为压坯密度修正值,g/cm3;p为成形压力,MPa。
2.7 木质粉末热压成形压力-密度应用模型
综上所述,杨木粉末和芦苇粉末热压成形过程的“压力-密度”模型应由理论方程和修正项2部分组成,其数学模型可描述为:
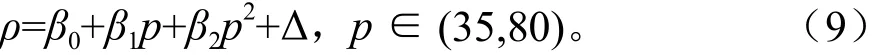
该模型可望拓展适用于所有木质。在实际应用过程中,可先计算确定β0、β1、β2,再将试验数据和理论计算数据对比得到密度修正值Δ。
图12所示为粒径小于0.85 mm的杨木粉末和芦苇粉末热压成形压坯密度随压力变化的实测数据、有限元计算数据和修正数据的对比图。不难看出,当成形压力不小于50 MPa时,经修正后的“压力-密度”关系曲线与实测“压力-密度”关系曲线高度一致,因而具有很好的实践应用价值。
3 结 论
通过杨木粉末、芦苇粉末等木质粉末的热压成形实验,利用有限元法分析了热压成形工艺条件下成形压力对压坯密度的影响。通过理论计算与实验检测相结合的方法,对成形压力与压坯密度的关系进行了回归分析,得到如下结论:
(1)在弹塑性理论的理想假设下,Shima模型可对杨木粉末、芦苇粉末等木质粉末的常温压制成形过程进行很好的数值模拟,与实验结果高度吻合。
(2)在成熟热压成形工艺条件下,Shima模型对杨木粉末、芦苇粉末等木质粉末的成形过程的有限元分析结果与实验检测数据有明显偏差,但该偏差在成形后期趋于定值。
(3)通过理论计算、实验检测与分析修正,获得的杨木粉末、芦苇粉末等木质粉末的的热压成形压力-压坯密度模型由理论方程与修正项组成,当成形压力不小于50 MPa时与实验结果高度吻合,可作为木质粉体热压成形模具设计与相关木质品制备工艺设计的计算依据,具有实际应用价值。
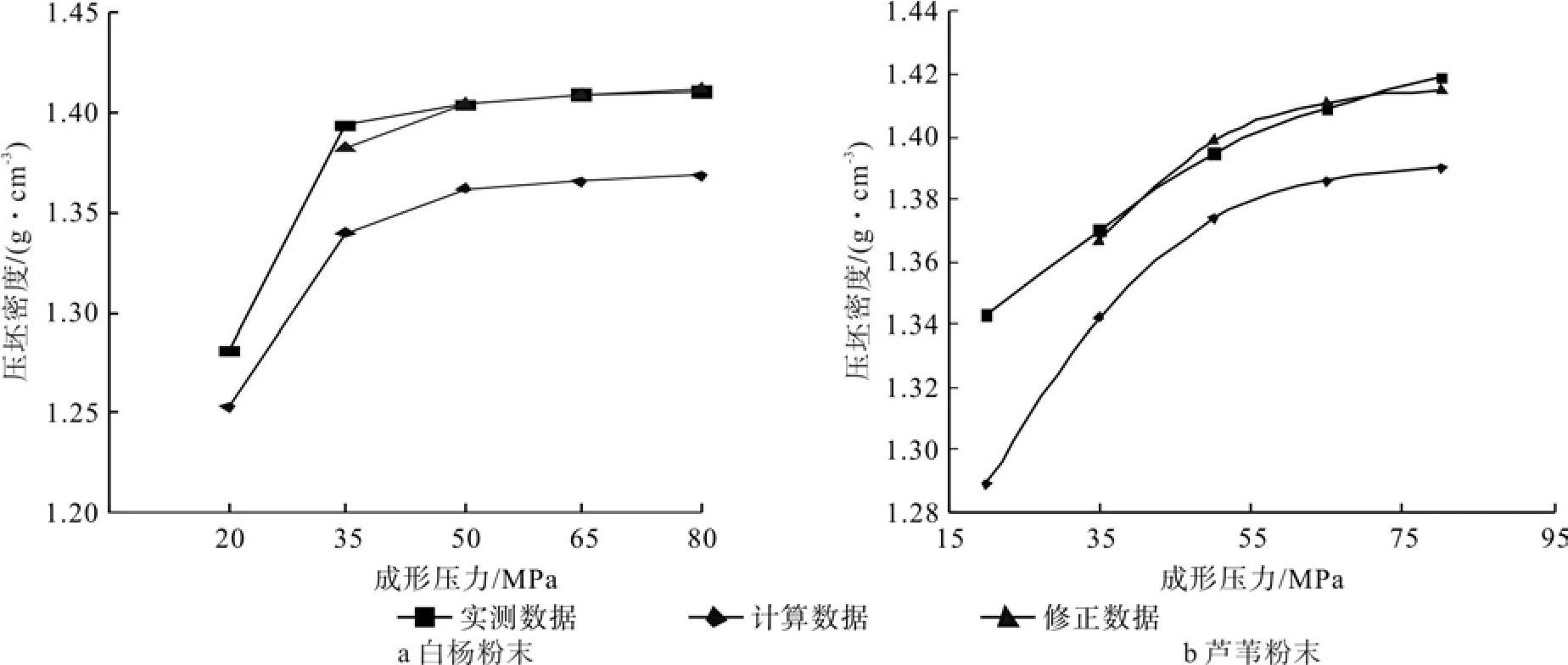
图12 压坯密度随压力变化的数据对比图Fig.12 Data comparison diagram of green density variation with pressure
[1]李元元. 金属粉末温压成形原理与技术[M]. 广州: 华南理工大学出版社, 2008.
[2]吴庆定. 木质粉末温压成形原理与技术[M]. 长沙: 湖南大学出版社, 2012.
[3]黄 静, 陈珏俐, 吴庆定. 白杨粉无胶模塑成形工艺参数优化[J]. 东北林业大学学报, 2012, 40(2): 81-84.
[4]张 红, 吴庆定, 彭 博. C-stalk/Cu复合材料的温压成形与表征[J]. 中南林业科技大学学报, 2014, 34(8): 101-105.
[5]Kuhu H A, Downey C L. Deformation characteristics and plasticity theory of sintered powder materials[J]. International Journal of Powder Metallurgy, 1971, 7(1): 15-25.
[6]Shima S, Oyane M. Plasticity Theory for Porous Mctal[J]. Int.J.Mech. Sci., 1976, 18: 285-292.
[7]Doraicelu S M, Gegel H L, Gunasekera J S,et al. A new yield functions for compressible P/M materials[J]. International Journal of Mechanical Sciences, 1984, 26(9/10): 527-535.
[8]Kim K Y, Cho J H. A densification model for mixed metal powder under cold compaction[J]. International Journal of Mechanical Sciences, 2001, 43(12): 2929-2946.
[9]陈火红. MARC有限元实例教程[M]. 北京: 机械工业出版社,2005.
[10]王逢瑚. 木质材料流变学[M]. 哈尔滨: 东北林业大学出版,2008.
[11]杜 强. SPSS统计分析从入门到精通[M]. 北京: 机械工业出版社, 2009.
[12]宋志刚, 谢蕾蕾, 何旭洪. SPSS 16实用教程[M]. 北京: 机械工业出版社, 2008.
Numerical simulation of the densi fi cation process on thermoforming of wood powders
DONG Jun-hui, LIU Ke-fei, CHEN Fei, WU Qing-ding
(Hunan Provincial Key Laboratory of Engineering Rheology, Central South University of Forestry and Technology, Changsha 410004,Hunan, China)
To fi nd the densi fi cation rules of thermoforming of wood powders, based on experimental data of thermoforming of poplar and reed powders, the fi nite element method was applied to analyze the in fluence of forming pressure on green density of wood powders.The methods of theoretical calculation and experimental veri fi cation were combined to make a regression analysis of the relationship between forming pressure and green density. The results show that according to Shima model, the calculated data obviously deviate from the experimental results under the condition of thermoforming. A pressure-density model of thermoforming of poplar and reed powders is obtained by theoretical calculation, experimental detection and correction analysis, which is composed of a theoretical equation and a correction term. The model is particularly consistent with the experimental results when the forming pressure is not less than 50 MPa.
wood powder; thermoforming; densi fi cation; numerical simulation
S781.3
A
1673-923X(2016)04-0103-08
10.14067/j.cnki.1673-923x.2016.04.019
http: //qks.csuft.edu.cn
2015-09-07
国家林业公益性行业科研专项经费资助项目(201404508);湖南省自然科学基金/常德市联合基金资助项目(14JJ5018);湖南省工业支撑计划科技项目(2015GK3016);湖南省研究生科研创新项目(CX2015B301)/中南林业科技大学研究生科技创新基金资助项目(CX2015B23)
董俊辉,硕士研究生
吴庆定,博士,教授;E-mail:wudingle@126.com
董俊辉,刘克非,陈 飞,等. 木质粉末热模压成形致密化过程数值模拟[J].中南林业科技大学学报, 2016,36(4):103-110.
[本文编校:吴 彬]

