森林火灾现场图形面积量算方法的比较研究
张民侠,张 洁,赵浩彥,陈戈萍
(南京森林警察学院,江苏 南京 210023)
森林火灾现场图形面积量算方法的比较研究
张民侠,张 洁,赵浩彥,陈戈萍
(南京森林警察学院,江苏 南京 210023)
森林火灾面积是森林火灾案件定罪量刑的依据,是确定森林火灾类型的重要条件,是森林火灾损失调查的重要因子。当绘制好森林火灾现场图形后,可采用几何法、网点法、方格法或求积仪法等量算面积,不同方法量算的结果不同,目前对不同方法量算结果的差异性研究较少。通过对不同方法量算精度的理论分析及实证研究发现,方格法量算的结果精度较高,但要选择合适的方格边长,效率较低;求积仪法使用效率高,操作方法得当,精度也可满足林业测量要求,但基层森林公安机关使用较少;几何法因有现成的公式,使用方便,但与图形的分割方式、量测方法、图形边长大小等有关。实践中要根据具体情况选用合适的量算方法,提高面积计算的精度。
森林火灾;现场图形;面积量算;定性处罚
森林火灾现场面积大小是森林火灾案件定性处罚的重要依据,是森林火灾类型确定的重要条件,也是森林火灾损失评估的重要项目之一。《国家林业局、公安部关于森林和陆生野生动物刑事案件管辖及立案标准》([2001]156号)规定了根据过火有林地面积或伤亡人数,确定放火案和失火案刑事案件的立案标准及案件性质。其中放火案过火有林地面积2 hm2以上为重大案件,过火有林地面积10 hm2以上为特别重大案件;失火案过火有林地面积2 hm2以上即立刑事案件,过火有林地面积10 hm2以上为重大案件,过火有林地面积50 hm2以上为特别重大案件。《森林防火条例》(2009年1月1日)第40条规定,按照受害森林面积和伤亡人数,将森林火灾分为一般森林火灾、较大森林火灾、重大森林火灾和特别重大森林火灾,不同类型的森林火灾要求相关部门采取不同的应对措施。《森林火灾损失评估技术规范(试行)》(国森防办〔2011〕17号)中强调火场面积和受害森林面积是损失评估的重要内容,火灾损失评估结果直接影响到相关责任人承担的责任大小,对推进森林防火工作具有重要的意义。
森林火灾现场面积数量通常由具有相应资质的司法鉴定机构组织人员或有一定资质的林业技术人员测量,出具鉴定意见或调查结果,作为确定森林火灾案件性质、森林火灾类型及损失大小的依据。实践中面积测量的方法很多,通常可分为直接求算法和间接求算法。直接求算法是指使用相关仪器设备直接测算出现场面积,如全站仪测量法、GPS测量法[1]等。间接求算法是指先在纸上绘制现场图形,然后在图上量算面积,如罗盘仪导线测量法、遥感影像图勾绘法[2]、地形图勾绘法等。森林火灾现场图形绘制好后,可以使用方格法(网点法)、求积仪法和几何法量算其面积。方法不同计算的结果不同,相关法律法规没有对量算方法进行规定。因此,鉴定人员要认真分析不同方法的适用条件、优缺点、精度等,保证鉴定结果客观准确,以维护司法的公正性[3]。本研究拟比较几种图上量算森林火灾图形面积方法的差异性,为林业司法鉴定提供依据。
1 材料与方法
试验地选在南京森林警察学院校园内,校内有高低起伏的丁山,山体海拔高度约为100 m左右,实验区坡度平均为15 °左右。山上树木主要为马尾松和阔叶树形成的混交林,平均郁闭度约为0.6。校园内也有较为开阔的平坦地面。在山上和平坦地分别设置两块样地。样地1为山地条件,在其边界设置了50个控制点;样地2为平坦地面,在其边界设置了39个控制点。每个样地分别使用全站仪和罗盘仪进行测量,以全站仪测量的结果为真值。罗盘仪外业依次测量了相邻控制点的距离、角度后,在室内进行绘图,对绘制好的图形,分别采用方格法、求积仪法、几何法计算其面积,每种方法重复量测30次。
1.1 方格法
方格法是利用透明方格纸覆盖在所绘制的图形上或直接将图形绘制在方格纸上,求算图形面积的方法。计算面积时,查数图形内方格数,再加上位于图形边界上方格数的一半得出总方格数。根据每个方格的面积和方格总数求算图形总面积。本研究中方格法使用的方格边长为5 mm。
1.2 求积仪法
求积仪法是用求积仪直接量测图形面积。求积仪有机械求积仪和电子求积仪,现在常用的是电子求积仪。电子求积仪也称为数字求积仪,是为传统的机械求积仪加上处理器进行重新设计而成为一种新型求积仪,求积仪的基本原理不变。由于微电子技术的引入,配合电子计算器,使求积仪的精度和效率大为提高。仪器操作时,手扶描迹器跟踪图形的轮廓,在显示器上就可获得所量测图形的面积。本研究中使用的求积仪是日本的KP-90N无极式求积仪。
1.3 几何法
几何法计算图形面积常用的有几何图解法、几何解析法、积矩法。几何图解法是将待测的图形分解成若干个简单的几何图形(三角形、四边形、梯形等),分别进行面积测算,其和为即所求图形的总面积。几何解析法也称为坐标法,是利用图形转折点的坐标计算面积。积矩法(纵距和法、平行线板法、截线法)是用由等距离的若干条平行线所组成的透明纸或透明模片测定面积的方法,将透明纸或透明模片随机覆盖在图形上,整个图形被平行线分割成若干个等高的矩形(或梯形),求出各矩形(或梯形)的面积,其和即为待测图形的总面积。本研究中使用几何图解法求算图形的面积。
2 结果与分析
2.1 不同方法计算面积的精度分析
2.1.1 方格法计算面积的精度分析
方格法求算图形面积的精度与方格的边长大小有关,方格边长愈小,求算的面积愈接近真实值,但方格边长过小又会增加计算的工作量,会失去使用方格法计算简便的优势。实际工作中应根据需要,从既考虑精度又节省工作量两方面,确定方格的边长。以前多采用“试验比较法”[4]来确定合适的方格边长,此法比较麻烦,且不能确定出测量的误差,不能保证计算的质量。通过研究发现,格点法求算图形面积的精度较方格法高[5]。格点法与方格法求算面积的思路基本一致,通过对格点法求算面积方法的精度分析,以探讨方格法中方格边长的大小及精度。
方格法求算图形面积公式为:

格点法求算图形面积公式为:

式(1)与式(2)中:N是图形中完整方格的个数;L是图形中不完整方格的个数;S是一个方格所代表的面积;A是所求图形的面积。
在待测图形边缘内外各做一个格点多边形,使:

式(3)中:A1是待测图形内格点多边形面积;A2是待测图形外格点多边形面积。若以(A1+A2)/2代替A,则有

即当用待测图形内外两格点多边形面积的平均值代替量测图形的面积,其最大误差不超过内外两个格点多边形面积差的一半。由于格点的距离愈小,两格点多边形面积的差值也越小。因此可通过限制格点的距离来限制格点法求积的误差,从而做出符合要求的估计。
由(2)式可得:

而N2=N1+L1。
则

给定测量允许的相对误差,则由(6)式可以确定格点的距离,再用(5)式计算面积。
例:令精度≥95%,即误差Δ≤5%,则
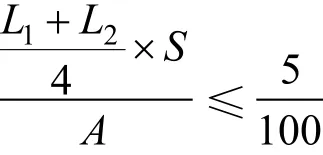
即

为方便讨论,假设所量测的图形为圆形,令:
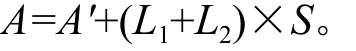
由(7)式可得

则

格点法中点的距离类似于方格法的边长,根据以上分析。如果按所测图形直径的十分之一确定方格的边长,可以获得≥95%的精度。同理,如果按所测图形直径的二十五分之一确定方格的边长,可获得≥98%的精度;按所测图形五十分之一确定方格边长,可望获得≥99%的精度。因此,从理论上分析,如果选用了合适的边长,方格法计算面积的精度可以满足林业测量的要求。
除此之外,影响面积量算的精度的还有方格纸放置的位置、计数方法、方格纸的伸缩等因素。放置时方格的边应尽量与图形边界重合或先靠一边重合,减少半格的数量,从而减少估算带来的误差;计数时采取复合量计数,减少对方格的遗漏;尽量将图形直接画在方格纸上,减少方格纸的伸缩;重复多次计数取平均值等,提高量算面积的精度。
用方格法求算面积,不需要复杂的仪器和高深的知识,使用方便,计算简单,受到了基层森林公安民警的欢迎。经笔者调研,目前林业司法鉴定中涉案林地面积求算方法中,有30%的案件都是将现场勾绘在地形图上,然后使用方格法计算面积。
方格法计算图形面积的缺点是,由于落在图形边界线上的方格要估读,加上方格边长及图形大小的不同,会影响图形计算的精度。格点法作业效率比方格法提高0.5~1倍,精度(0.14%)可提高1倍以上[5],建议实践中也可以使用格点法量算图形面积。
2.1.2 求积仪法计算面积的精度分析
KP-90N属于脉冲式求积仪,求积仪的积分导轮与图面接触,摩擦使其正转或反转,编码器产生脉冲增量,计数器接收并经微处理器处理,最后显示所测图形的面积值。KP-90N求积仪量测面积示意如图1。

图1 KP-90N求积仪测面积示意Fig.1 The area of graph was calculated with KP-90N product moment method
描迹器由a移动到a1时,可将其分解为:先由a平移到b,此时求积仪计算的面积为L·h(L为描臂长度,h为积分导轮转动的弧长);再由b移动到a1,求积仪计算出的面积为1/2L2·θ。描迹器绕图形移动一周后,所量测的图形面积为:

式(8)中:Σθ=0,Σh为积分导轮转运的总弧长,即Σh=2πr·n(n为积分导轮转运圈数)。则得:

式(9)中:t为脉冲当量值(比例尺1∶1时,t=0.1 cm2/脉冲);K为积分导轮每转一圈所计的脉冲数(K=1 080)。
则求积仪量算面积的基本公式为:

对式(10)全微分得:

积分导轮的半径误差dr与制造的材料有关,一般情况下厂家都会对其进行特殊处理,所以可以认为dr=0,同时Σθ=0,所以上式可简化为:
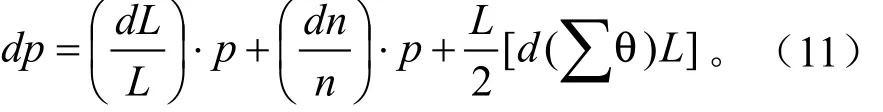
从式(11)可知,KP-90N求积仪面积量测误差由固定误差和比例误差(与面积成正比)组成。求积仪扫描臂长L=18 cm,描迹镜放大倍数为1.5倍,那么描迹误差为:0.01/1.5=0.006 7 cm;式(11)中dL可认为是描迹误差,则dL/L=0.000 37。式(11)中d(Σθ)·L的值可认为是起、终对点误差,其值也为0.006 7 cm。积分导轮转动圈数误差dn与仪器分解力(小于1/500个脉冲)有关,同时也与所量测图纸的质地有关,图纸的摩擦系数越大,则dn的值就越小。实践证明,在专用绘图纸上量测面积dn/n≤1/1 000,若使用较光滑的图纸dn/n≤1/500。综上所得,KP-90N电子求积仪量算面积的精度为:

式(12)中比例系数K取值范围为0.001至0.002,主要取决于量测图纸的性质。如在采用打毛处理的聚脂薄膜上量算,K可取0.001。不同面积的量算精度见表1。

表1 不同面积的量算精度(K=0.001)Table 1 The calculation precision of different size of land(K=0.001)
从表1可以看出,KP-90N电子求积仪量测面积大于20 cm2的图形面积时,其相对精度可达到1/250,林业上一般要求的精度是1/200。因此,使用求积仪时,建议量测的面积应该在20 cm2以上。
汤明宝[6]等人通过研究,发现求积仪量算大面积的图形效率很高,量算的精度可达0.2%以下,量算面积小于50 cm2的图形时,其相对精度大于0.3%,量算面积小于10 cm2的图形时,应选择方格法或几何法。使用时还需要测定分划值的变形系数,以消除脉冲误差以及图纸变形误差对面积量算结果的影响。求积仪分划值变形系数的输入与比例尺的安置同步进行[7]。在量算面积过程中,要减小积分导轮最少的滑动,以提高量测的精度。
2.1.3 几何法计算面积的精度分析
几何图解法计算面积的精度与图形的分割方式及量测的方法有关,一般图形分割的个数越少、分割的线条越长,计算的结果精度越高。张晋昌[8]等人的研究发现,绘图比例尺对计算结果也有影响,当绘图比例尺增大一倍,量算面积的精度大致提高一倍。
几何解析法计算面积的精度与测量的精度有关,其面积计算公式[9-10]如下。

或

当i=1时,yi-1=yn,xi-1=xn;当i=n时,yi+1=y1,xi+1=x1。
式(13)(14)中:P为图形量算的面积;x、y为图形边界转折点的坐标;n为图形边界转折点的个数;i为图形边界转折点的序号。
对式(13)或(14)求导并设各点误差相等,根据误差传播定律可得面积量算的中误差mp为:

设
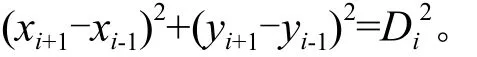
假设量测的图形为正多边形,由图2可得:

图2 Di计算示意Fig.2 Calculation diagram of Di

则

已知正多边形的面积P为:

由式(16)求得多边形的边长Si为:

将式(17)代入式(15),得:


表2 不同边长的面积计算精度Table 2 The calculation precision of the areas consisted of different side length
从表2可以看出,面积计算的精度与多边形的边数有关,边数越多,面积精度越高,但四边形例外。朱宏军[11]等人的研究发现,当正多边形接近圆形,面积计算的相对精度较高,并且精度随面积的增大而增加。但当比例尺变小,图形面积变小时,面积计算的相对误差会增加。所以实际计算时,当森林火灾现场边界勾绘在地形图上,边界为曲线时,在边界上选点分割为多边形时,要确定合适的点数,并不是越多越好。段庆功[12]等人的研究发现,比较合适的分割间距应该是0.3~0.5 m。朱宏军[13]等人研究也发现,解析法计算的精度高于图解法。
积矩法(纵距和法、平行线板法、截线法)求算图形面积的方法如图3所示。

图3 积矩法求算图形面积示意Fig.3 Product mement method schematic diagram
放置时图形位于透明纸或透明模片的中央,而且要使边缘a,b两点位于任意平行线之间,整个图形被平行线分割成若干个等宽的矩形或等高的梯形,图内的平行线段是各个矩形的长度或梯形的中线,如cd、eg、……kl。当表示为梯形时,图形中的虚线为各个梯形的上、下底。各个矩形或梯形面积的和即为图形的总面积[14]。积矩法求算面积的公式如下。

式(19)中:P为所求图形的总面积;h为矩形的宽度(梯形的高),即平行线的间距;括号中为纵距和(矩形的宽度或梯形的中线之和)。
陶绍训[15]的研究发现,用平行线板测定面积的精度比网点板好,而且可以根据需要制作成求积尺,量算的效率会大大提高。陈禄泽[16]研究发现,纵距和法量算面积的最大误差不超过1/200,一般在1/500左右,最高精度常出现在1/1 000以上,高于森林罗盘仪测量容许误差1/200,可以满足林业测量的精度要求。
2.2 不同方法计算结果的实证分析
2.2.1 样地1测量结果比较分析
对样地1测量的面积数据进行方差分析,结果见表3。

表3 4种方法测量坡地面积结果的方差分析Table 3 The ANOVA of slope land areas calculated with four methods
从表3可以看出,全站仪法、方格法、求积仪法、几何图解法测量面积的结果存在显著差异。具体哪几种方法存在差异,使用费歇最小显著差方法(LSD)进一步分析,结果见表4。
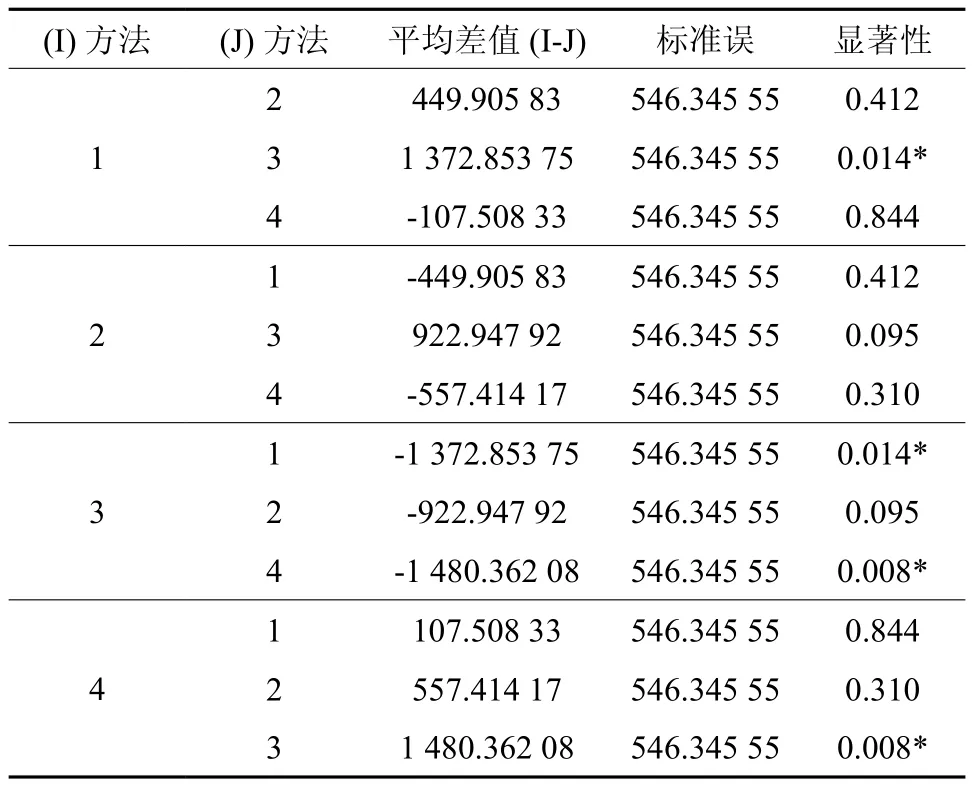
表4 LSD 多重比较†Table 4 Multiple comparison analysis with LSD
从表4可以看出,几何图解法分别与方格法和全站仪法测量的结果存在显著差异,与求积仪法也有一定的差异。表明与其他3种方法相比,几何图解法量算图形面积的误差较大。具体哪一种方法误差最小、精度最高并具有较高的稳定性,以全站仪测量的面积结果为真值,选取了30个样本的均值、标准差、相对标准偏差、平均相对误差和平均相对误差绝对值5个指标来比较与方格法、求积仪法和几何图解法3种方法的差异,结果见表5。

表5 3种方法测量坡地面积的数据分析Table 5 Data analysis of slope land areas calculated with three methods
从表5可以看出,方格法量算面积的标准差和相对标准偏差最小,求积仪法次之,几何图解法最大,表明方格法量算面积的数据变动最小,量算结果最为稳定,几何图解法量算的面积数据变动最大,量算结果较不稳定。方格法量算面积的平均相对误差和平均相对误差绝对值最小,求积仪法次之,几何图解法最大,表明方格法量算面积误差最小,精度最高,几何图解法量算面积误差最大,精度最低。
2.2.2 样地2测量结果比较分析
对样地2测量的面积数据进行方差分析,结果见表6。

表6 4种方法测量平地面积结果的方差分析Table 6 The ANOVA of flat ground areas calculated with four methods
从表6可以看出,4种方法测量结果的显著性大于0.1,表明方格法、求积仪法、几何图解法和全站仪法所测量的面积不存在显著差异。使用费歇最小显著差方法(LSD)进一步分析,结果见表7。
从表7可以看出,虽然4种方法不存在明显差异,但是以全站仪法测量的结果为真值,通过比较其余3种方法量算面积结果与其的差值,可以发现方格法量算的面积最接近真值,求积仪法次之,几何图解法误差最大,这与样地1分析的结果一致。具体哪一种方法误差最小、精度最高并具有较高的稳定性,同样以全站仪测量的面积结果为真值,选取30个样本的均值、标准差、相对标准偏差、平均相对误差和平均相对误差绝对值5个指标来比较与方格法、求积仪法和几何图解法3种方法的差异,结果见表8。

表7 LSD多重比较†Table 7 Multiple comparison analysis with LSD
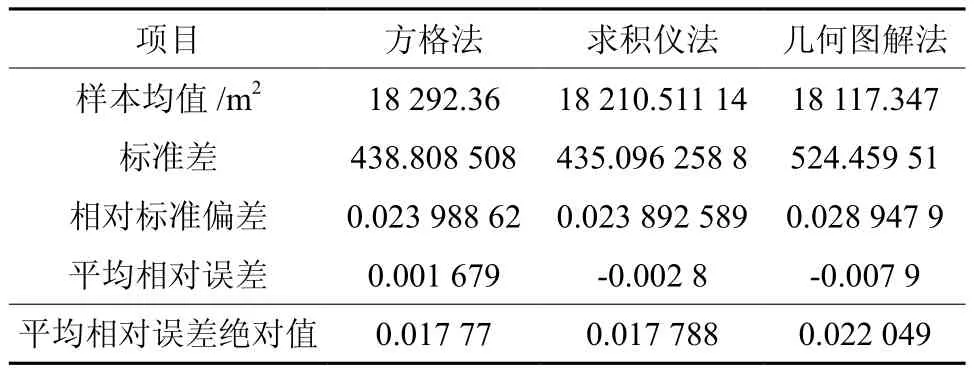
表8 3种方法测量平地面积的数据分析Table 8 Data analysis of flat ground areas calculated with three methods
从表8可以看出,方格纸法和求积仪法量算图形面积的标准差和相对标准偏差较小,几何图解法较大,表明方格纸法和求积仪法量算图形面积的数据变动较小,量算的结果最为稳定,几何图解法量算的结果较不稳定。方格法量算面积的平均相对误差和平均相对误差绝对值最小,求积仪法次之,几何图解法最大,表明方格法量算面积误差最小,精度最高,几何图解法量算面积误差最大,精度最低。
为了进一步比较3种方法量算图形面积的差异性,以全站仪测量的结果为真值,计算不同方法量算结果的误差与精度,结果见表9。
从表9可以看出,方格法、求积仪法、几何图解法量算的结果与前面的分析结果一致,即方格法效果最好,其次是求积仪法,最后是几何法图解法。同时也发现,样地2量测结果的误差小于样地1,精度高于样地1,主要原因是样地1所处地形为山地,罗盘仪导线测量法测量的精度本身低于全站仪,而样地2处于平坦地面,罗盘仪导线测量法的效果较好。因而外业测量的精度首先会影响到图形绘制的精确程度,绘制的图形与现场越接近,面积计算的结果精度越高。

表9 不同方法测量结果的差异性比较Table 9 Difference comparison among the results of different methods
3 结论与讨论
3.1 结 论
(1)根据精度分析,方格法、求积仪法、几何法都可以满足图形面积量测的精度要求,可作为森林火灾现场图形面积量算的方法。《森林资源规划设计调查技术规程》(GB/T26424-2010)中关于面积量算部分就特别指出“手工绘制成果图时,可用几何法、网点网格法或求积仪等量算面积”。但研究发现,不论使用哪种方法都要注意规范操作,避免降低精度的不利因素,以提高量算结果的准确度。
(2)根据实证研究分析,外业测量的准确度影响面积量算的结果。外业测量时控制点选择与现场形状越接近、角度和距离测量的越准确,绘制的图形越精确,求出的面积则越精确。
(3)根据实证研究分析,方格法量算的结果最精确,其次是求积仪法,几何图解法量算的结果误差最大,结果不稳定。
3.2 讨 论
(1)使用方格法时要选取合适的方格边长,将方格纸与图形充分贴合;通过调整方格纸的位置使方格尽量占满图形,减少逐个计数的工作量,使落在图形边界上的方格数达到最少,因方格法的误差主要源于界线上半个方格数估算的误差;数方格时要认真仔细,防止方格纸移动。本研究中图形是绘制在方格纸上,因此量算结果较精确。计方格数量时多数几次取平均,有条件的时候可使用网点法则效果更好。方格法或网点法量算面积的效率低,数方格时容易疲劳,可制作带有一定色彩的方格,保证计数准确。
(2)使用求积仪量算面积效率高。但使用时应注意将图纸固定在光滑平整的桌面上,绘图的图纸不能太光滑,要有一定的摩擦力。操作时要保证桌子平稳;用描迹器跟踪图形边界时手要稳,跟踪标志不能离开图形边界线,速度要适当;跟踪时起始位置与终点位置要充分重合;操作时中间可以暂停,以便随时调整手力、运动方向和视力,保持好身体的重心;最好多测几次取平均值,以提高量算的精度;量算的面积应大于20 cm2。由于求积仪的购置需要一定的费用,目前基层森林公安很少使用。
(3)几何法适合于较为规则的几何图形面积的量算。如果是曲线形的图形,如地形图勾绘形成的图形不宜使用,因直线趋近程度差,通常会降低面积量算的精度。使用几何图解法量算面积的误差与图形的分割方式、量测方法有关,尽量使分割的图形个数少,分割的图形线条长,以减少分割和量测带来的误差。本研究中几何图解法量算的误差较大,与图形分割不精确有一定的关系,部分分割的图形线条过短,人为做高等过程中都存在误差,导致面积计算结果精度不高。几何解析法量算的精度较高,但外业测量时要确保坐标测量准确。积矩法(纵距和法、平行线板法、截线法)使用效果好,精度较高,建议可以使用。
森林火灾现场面积测量的方法较多,《森林火灾成因和森林资源损失调查方法》(LY/T1846-2009)中指出“一般森林火灾和较大森林火灾,用罗盘仪、经纬仪[17]或经过差分纠正的GPS接收机测量,测量的闭合差不大于1/200;重大森林火灾和特别重大森林火灾,可以分成小区域用罗盘仪、经纬仪和GPS接收机测量;特别重大森林火灾也可以借助飞机进行航空测量”。不同方法测量结果不同,但从对森林火灾定案的角度,司法鉴定结果需要唯一性。因此需要不断研究各种方法的适用条件、精确度,保证鉴定结果的公正性和客观性。在司法实践中还需要考虑测算的时间效率。本研究从理论分析和实证方面对森林火灾现场图形面积量算方法进行了比较研究,但实证研究范围和方法还有一定的局限性,今后还可以进一步扩大研究范围,对多种测算方法的差异性进行比较研究,为林业司法鉴定提供依据。
[1]汪 东, 周宏平,张慧春,等.不同植被 GPS 定位精度影响因素分析及多路径效应[J].中南林业科技大学学报,2014,34(11): 46-51.
[2]巩垠熙,高 原,仇 琪,等.基于遥感影像的神经网络立地质量评价研究[J].中南林业科技大学学报,2013,33(10):42-48.
[3]乐通潮,鲍晓红,万晓会,等.3S技术在林业司法鉴定中的应用[J].防护林科技, 2008(3):72-73.
[4]林业部调查规划院.森林调查手册[M].北京:中国林业出版社,1980.
[5]汤明宝.格点法量算面积的原理和精度[J].测绘学报,1987,16(1): 57-67.
[6]汤明宝.提高求积仪量算面积的精度[J].测绘学报,1984,13(1): 42-53.
[7]常同元.KP-90N电子数字求积仪分划值变形系数的测定方法[J].冶金测绘,1994,3(4):52-53.
[8]张晋昌. 面积量算及其精度分析[J]. 运城学院学报,2003,21(5):38-39.
[9]林观土,陈俊林. 农地面积测量方法的精度分析[J]. 广东农业科学,2007(6):44-46.
[10]郭宗河,郑进风. 全站仪面积测量及其精度分析[J]. 测绘通报,2002(3):30-31.
[11]朱宏军,安忠利.用坐标法量算士地面积的精度分析[J].黑龙江水利科技,2000(4):56-57.
[12]段庆功,李海君. 含有曲线的土地面积量算精度分析[J]. 价值工程,2015(10):222-223.
[13]朱宏军,安忠利.用坐标法量算士地面积的精度分析[J].黑龙江水利科技,2000(4):56-57.
[14]张民侠,刘成林,李炳凯,等.森林资源管理概论[M].北京:中国人民公安大学出版社,2015.
[15]陶绍训. 网点板与平行线板测定面积的方法与精度[J].林业资源管理,1983(5):5-8.
[16]陈禄泽. 用纵距和法求面积精度高[J].林业勘查设计,1974(7): 25.
[17]曹 忠,冯仲科,徐伟恒.电子经纬仪无损立木材积测量方法及精度分析[J].中南林业科技大学学报,2015,35(4):7-13.
The comparison among the calculation methods of forest fi re spot fi gure area measuring research
ZHANG Min-xia, ZHANG Jie, ZHAO Hao-yan, CHEN Ge-ping
(Nanjing Forest Police College, Jiangsu 210023, Nanjing, China)
Forest fire area is the gist of conviction and measurement of penality of forest fire crimes, the important condition of determining the types of forest fi re, and the signi fi cant factor of investigating the loss of the of forest fi re. After drawing the forest fi re fi eld graph, the geometric method, dot method, grid method, and the planimeter method etc. can be used to calculate the proportion.The results are different after using different methods. Currently, there is a small amount of studies of differences among the results.Through theroatical analysis and empirical study of different measurements, the grid method has a relative high accuracy. However, the applicable gird length is needed so the ef fi ciency is low; using planimeter method is quite ef fi cient, operationally appropriate and the accuracy is apply to the requirements of forest measurements. But the fundemental forest public security organizations utilize few of planimeter method. Geometric method has existing formulas and is easy to use but it dependes on the ways of segmentation, methods of measurements, and the size of graph length. In the practice, choosing suitable measurement ways to improve the accuracy of calaculaing area according to speci fi c situation is required.
forest fi res; the spot fi gure; area measuring; qualitative punishment
S771
A
1673-923X(2016)12-0018-08
10.14067/j.cnki.1673-923x.2016.12.004
http: //qks.csuft.edu.cn
2016-06-29
中央高校基本科研业务费专项(LGYB201511);江苏省林业三新工程项目(LYSX[2016]52)
张民侠,副教授,博士
张 洁,副教授;E-mail:282898412@qq.com
张民侠,张 洁,赵浩彥,等. 森林火灾现场图形面积量算方法的比较研究[J].中南林业科技大学学报,2016, 36(12): 18-25.
[本文编校:文凤鸣]

