风速对红松针叶床层两个重要失水时间的影响
金 森,张俪斌,于宏洲,满子元
(东北林业大学 林学院,黑龙江 哈尔滨 150040)
风速对红松针叶床层两个重要失水时间的影响
金 森,张俪斌,于宏洲,满子元
(东北林业大学 林学院,黑龙江 哈尔滨 150040)
森林防火人员需要关注可燃物从雨后不燃变为可燃所需的时间和其后蔓延速率倍增所需的时间。这两个时间与可燃物失水速率直接相关,也会受风速影响。但关于风速对这些时间的影响还没有直接研究。为此,以红松针叶床层为研究对象,研究其在近恒温湿条件下不同风速时的失水过程,分析风速对这两个失水时间的影响,结果表明,在温度近20 ℃,湿度在25%~35%的条件下,有风条件显著减少了红松针叶床层从雨后不燃(含水率70%)到可燃所需的时间,时间可缩短1~1.3 h,减少比例近40%,最长可缩短5.2 h。但不同风速所缩短的时间差异不大。风的这种影响与红松针叶床层的密实度有关。风的影响可用风速的指数函数形式来描述。但风对于以0.3 g·g-1为基点的蔓延速率倍增所需时间无显著影响。
风速;失水时间;阔叶;含水率;蒙古栎;可燃物
风是重要的火险预报因子。风通过影响可燃物含水率和火行为而增加火险。风对火行为的影响已有很多研究[1-2]。风对火险的影响可分为两个方面:一是在可燃物含水率较高而不燃时,风加速可燃物的失水速率,缩短从不燃到可燃的时间;二是在可燃物可燃后,风加速失水速率,加速林火蔓延速率。基于物理意义的火险预报及等级划分需明确两个时间:一个是某种可燃物从不燃变为可燃所需的时间,典型的是从雨后不燃到可燃所需的时间,另一个是可燃物含水率减少导致蔓延速率倍增所需的时间。前者用于确定可燃物何时可燃,后者用于基于物理意义的火险等级划分。这两个时间与可燃物失水速率有关,必然受风速的影响。目前关于风对可燃物含水率变化过程的影响已有一定研究[3-9],但关于风对这两个时间的影响的直接研究还没有开展,还不明确风对这两个时间的减少幅度。
红松Pinus koraiensis是东北地区的原生植被的优势树种,研究风对红松林可燃物上述两个时间的影响,对于建立相应的火险预报方法和森林防火实践具有现实意义。为此,我们以红松针叶床层为研究对象,研究其在近恒温湿条件下不同风速时的失水过程,分析风速对上述两个失水时间的影响,为建立更科学的火险预报系统提供基础。
1 研究方法
1.1 采 样
红松针叶采自东北林业大学帽儿山实验林场。 该 林 场 位 于 45°20′~ 45°25′N,127°30′~127°34′E,属温带大陆性气候,阔叶红松林为该地区原生植被。该林场目前主要是原生植被大量破坏后形成的天然次生林。在红松林下采集当年凋落的红松针叶,带回实验室自然风干。
1.2 室内失水实验
风速设0、1、2、3、4 m·s-1五个梯度,床层密实度设0.015 8、0.023 6、0.031 5三个梯度,共15个风速密实度组合,每个组合3个重复,全部试验共构建45个床层。对于每个风速,取部分红松松针置于烘箱中105 ℃烘24 h至绝干,分别取干质量为4、6、8 g的松针各3份,在盆中浸泡24 h,取出放置一段时间,待针叶失去部分表面水分后制成长20 cm、宽20 cm、高2 cm的可燃物床层,该床层高度与采样地红松林下可燃物床层的高度相似。红松的颗粒密度按317.2 kg·m-3计,则4、6、8 g的松针床层的密实度分别为0.015 8、0.023 6和0.031 5。每个床层上下两面用塑料网固定,下面和四周用塑料布围住,只有上表面能够进行水分散失。将松针床层放在架子上,置于风扇前,调整床层与风扇的距离,使床层上方的风速为设定风速。然后每隔0.5 h称量一次床层的质量,精确到0.01 g,共称量20次。同时记录环境温度和湿度。
1.3 数据处理与分析
1.3.1 可燃物含水率的计算
按下式计算各床层不同时刻含水率:

式(1)中:Mi为阔叶床层的含水率,g·g-1;Whi为第i个时刻称量的阔叶鲜质量,g;Wd为阔叶干质量,g。
1.3.2 两个失水时间计算
为计算两个失水时间,必须先设定各自的基准含水率。第一个时间的基准含水率为一般可燃物在中度降雨量(10 mm)后能到达的含水率,根据对相似可燃物雨后含水率变化的观测结果[10-11],将该值设为0.7 g·g-1。根据蒙古栎点燃含水率的试验结果[12],将点燃含水率设为0.3 g·g-1。相应的点烧试验[13]证明了Rothermel模型[1]在预测蒙古栎红松混合床层蔓延速率中的有效性。据此模型计算,以含水率为0.3 g·g-1时的林火蔓延速率为基准点,倍增时的含水率为0.2 g·g-1。为此,分别计算不同风速下红松针叶各床层含水率从0.7 g·g-1下降到0.3 g·g-1、从 0.3 g·g-1下降到 0.2 g·g-1的时间。这些时间分别为中等强度降雨后从不燃到可燃所需的时间、林火蔓延速度倍增所需的时间。
1.3.3 风速对两失水时间的影响分析
以风速和密实度为自变量,对上述两个失水时间进行方差分析,确定对其有显著影响的变量。以对其有影响的变量为自变量,建立该变量和相应失水时间的拟合函数。拟合通过MATLAB7.0实现。
2 结果与分析
2.1 红松针叶床层的失水时间
全部试验温度范围为17.5 ~19.6 ℃,单次实验的变幅均值为2.0 ℃,湿度范围为0.247~0.344 g·g-1,单次实验变幅均值为 0.097 g·g-1。这是东北林区防火期中的典型气象条件。
图1给出了不同风速、不同密实度时红松针叶床层含水率从 0.7 g·g-1到 0.3 g·g-1、从 0.3 g·g-1~0.2 g·g-1两个失水过程的失水时间。从趋势上看,从雨后不燃到可燃所需时间基本随风速增加而下降,而以含水率0.3 g·g-1为基准的蔓延速率倍增所需时间与风速没有明显关系。从数值上看,含水率从 0.7 g·g-1到 0.3 g·g-1所需时间,密实度为0.015 8和0.023 6的床层无风时均值相似,基本为3.5 h,而密实度为0.031 5的床层的时间较长,为8.4 h。随风速增加,不同密实度的床层平均失水时间在2.2 h到3.2 h之间, 其中密实度为0.015 8和0.023 6的床层的失水时间有风均值在2.2 h到2.5 h之间,而密实度为0.031 5的床层稍长,为2.4~3.2 h。有风时不同风速下该失水时间差异不大。而3种密实度的红松针叶床层含水率从0.3 g·g-1到0.2 g·g-1所需时间,即以0.3 g·g-1含水率时的蔓延速率为基准的倍增所需时间,均值多在0.5 h到1.0 h。有风和无风、有风时不同风速下的差异不明显。上述表明,风使红松针叶床层从雨后不燃到可燃所需时间平均至少减少1~1.3 h,减少比例近40%,最长可缩短5.2 h。而对于蔓延速率倍增所需时间则影响不明显。

图1 不同密实度、不同风速的红松针叶床层的两个失水时间(图中70%~30%为0.7~0.3 g·g-1、30% ~ 20% 为 0.3 ~ 0.2 g·g-1)Fig.1 Two water loss times of moisture from 0.7 g·g-1~0.3 g·g-1 and 0.3 g·g-1~0.2 g·g-1 of fuelbed composed of Korean pine needles of varied compactness
2.2 风速对两个失水时间的影响
表1给出了风速和密实度对两个失水时间影响的方差分析结果。从中可见,风速、密实度及其交互作用对红松针叶床层从0.7~0.3 g·g-1的失水时间有着显著影响,其中以风速的影响最大,其次为密实度,最次为两者的交互作用。对于0.3~0.2 g·g-1的失水过程,风速、密实度和风速与密实度的交换作用对其都没有显著影响。

表1 风速和密实度对红松针叶床层两个失水时间的方差分析结果Table 1 Variance analysis of effects of wind speed and fuelbed compactness on water loss times of two periods of fuelbeds of Korean pine needels
分别密实度,以风速为自变量,对应的3个可燃物床层的从0.7 g·g-1到0.3 g·g-1的失水时间分别为因变量,采用不同形式的函数进行拟合建模,以所得决定系数R2最大为最佳模型。所得的最佳模型形式为:

式(2)中:T为0.7~0.3 g·g-1的失水时间,h;w为风速,m·s-1。
所得模型系数和拟合情况见表2和图2。从模型的决定系数看,预测值和实测值关系很密切,模拟有效。从图2的数据看,所建模型充分反映了两个失水时间随风速的变化情况。3个模型的均方根误差为0.5 h到0.8 h,平均相对误差在20%以内,精度可以接受。
上述3个不同密实度的床层上建立的风速对第一个失水时间的影响函数在形式上是一致的,表明了风对第一个失水时间的影响是一致的。如果为预测目的,应将密实度直接作为变量放入模型中。图3给出了表2中密实度和对应的模型系数a、b、c之间的散点图。从中可见,这些系数和密实度之间存在着抛物线的关系,为此,用下面的抛物线形式来拟合:

式(3)中:y为a、b、c,β为密实度;d、e、f为待估参数。因为只有3个样本,所以d、e、f可确定性计算出来。表3给出了相应的计算结果。

表2 风速对0.7~0.3 g·g-1阶段失水时间影响模型T=ae-bw+c的参数†Table 2 Coefficients of models between fuelbed water loss times of periods 0.7~0.3 g·g-1 and wind speed in the form of T=ae-bw+c

图2 根据风速计算的红松针叶床层叶床层0.7~0.3 g·g-1阶段失水时间比较Fig.2 Comparison of measured water loss times of two periods(0.7~0.3 g·g-1) and modeled ones for fuelbeds of Mongolian oak leave
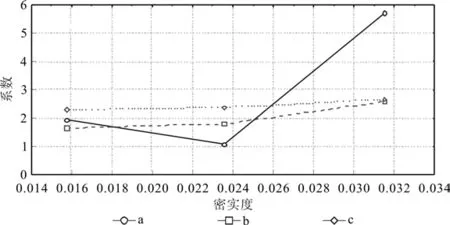
图3 床层密实度和相应3个拟合系数Fig.3 Fuelbed compactness and three corresponding coef fi cients of fi tting functions

表3 床层密实度和式(2)中参数的拟合系数Table 3 Coefficients of functions fitting coefficients in Eq.2) over fuelbed compactness
同时包括风速和密实度的第一个失水时间的预测模型为:

式(4)中符号意义同前。
该模型的平均绝对误差为0.415 h,均方根误差为0.537 h,平均相对误差为15.91%。模型的误差综合了分别密实度建立的3个模型,预测和实测的失水时间的决定系数为0.792,总体效果较好。图4给出了两者之间的对比,模型总体是无偏的,在失水时间<3 h时,误差较小,失水时间在4~5 h时,误差有所增加,最大可达1.2 h。

图4 实测和模拟的从 0.7 g·g-1 到 0.3 g·g-1 失水时间Fig.4 Observed and modeled water loss times of fuelbed from 0.7 g·g-1 to 0.3 g·g-1
3 结论与讨论
在温度近20 ℃,湿度在0.25~0.35 g·g-1的条件下,风显著减少了红松针叶床层从雨后不燃到可燃所需的时间,可缩短1~1.3 h,减少比例近40%,最长可缩短5.2 h。但不同风速所能缩短的时间差异不大。风这种影响与红松针叶床层的密实度有关。风的影响表现为指数函数形式。风对于以含水率0.3 g·g-1为基点的蔓延速率倍增所需时间无显著影响。
风对从0.7~0.3 g·g-1阶段所需时间有影响而对从0.3~0.2 g·g-1所需时间没有显著影响表明,风对红松针叶床层失水速率的影响主要体现在高含水率阶段。Jin等[14]表明,可燃物在高含水率时的失水过程主要受蒸发影响。本研究中红松针叶床层含水率从0.7~0.3 g·g-1阶段也以蒸发过程为主,而从0.3~0.2 g·g-1阶段以扩散为主,因此,风对红松针叶床层失水速率的影响主要体现在高含水率的蒸发阶段。
本研究建立的同时包括风速和密实度在内的第一个失水时间的预测模型[(式4)]反映了风和密实度对第一个失水时间的影响形式。但温湿度显著影响可燃物的失水速率,相应地影响失水时间。本研究的失水时间和风速、密实度对其的影响只是针对东北林区防火期中典型天气条件有效,仅适用于研究中的温湿度范围,今后应在更大的温湿度范围内开展同样的研究,以提高模型的适用性。
风速对第二个失水时间没有影响,这与我们的预想不同。一方面可能因为这个阶段可燃物含水率较低,以变成扩散为主的阶段,风的影响已很弱,同时,每个风速密实度组合的3个重复的结构有一定差异,这些差异掩盖了本来就不很大、至少不像对第一个失水时间那么显著的影响。这种影响也可能与材料本身的特性有关,针叶材料不明显,还可能与含水率的大小有关。这些都需要进一步研究。
[1]Rothermel, R.C. A mathematical model for predicting fi re spread in wildland fuels[R]. USDA For.Serv.Res.Pap, 1972,INT-115.
[2]李存宇,金 森,周 勇,等.红松针叶床层风影响因子的模拟[J].林业科学,2014,50(1):116-124.
[3]Byram GM.Solar Radiation and Forest Fuel Moisture[J].Journal of Agricultural Research, 1943(67):149-176.
[4]King AR,Linton M.Moisture variation in forest fuels: the rate of response to climate changes[J]. Aust. J.Appl. Sci. 1963, 14(1):38-49.
[5]BRITTON, CM, COUNTRYMAN CM, WRIGHT HA,et al. The effect of humidity, air tempera ture, and wind speed on fi ne fuel moisture content[J].Fire Technology. 1973,9(1):46-55.
[6]Van Wagner. A laboratory study of weather effects on the drying rate of jack pine litter[J].Canadian Journal of Forest Research,1979,(9): 267-275.
[7]居恩德,陈贵荣.可燃物含水率与气象要素相关性的研究[J].森林防火, 1993(1): 17-19.
[8]张国防,林文革,花昆福,等.杉木人工林地表易燃物含水率变化规律[J].福建林学院学报,2000,20(1):76-78.
[9]Saglama B, Bilgili E, Ku O,et al. Determination of surface fuels moisture contents based on weather conditions[J]. Forest Ecology and Management, 2006, 234: 75.
[10]张运林,张 恒,金 森.季节和降雨对细小可燃物含水率预测模型精度的影响[J].中南林业科技大学学报,2015,35(8):5-12.
[11]金 森,李建民.农林交错区典型地表死可燃物含水率预测[J].中南林业科技大学学报,2014,34(12): 27-34
[12]李 林.森林可燃物含水率及失水效率的研究[D]. 哈尔滨:东北林业大学,2004.
[13]张吉利,刘礡霏,邸雪颖,等.广义Rothermel模型预测平地无风条件下红松-蒙古栎林地表混合可燃物火行为[J].应用生态学报,2012,23(6):1495-1502.
[14]Jin S,Chen PY. Modelling drying processes of fuelbeds of Scots pine needles with initial moisture content above the fi bre saturation point by two-phase models[J]. International Journal of Wildland Fire, 2012,21:418-427.
Effects of wind speed on two key water loss times of fuelbeds composed of Korean pine needles
JIN Sen, ZHANG Li-bin, YU Hong-zhou, MAN Zi-yuan
(College of Forestry, Northeast Forestry University, Harbin 150040, Heilongjiang, China)
Two times concerned by forest fi re managers are the time required for fuel to become ignitable from non-ignitable status after rain and the time required to increase its spread rate by one time. These times have been related with fuel drying rate. Generally speaking, wind affect fuel drying rate and should affect the two times. Although some works have been conducted on effects of wind on fuel moisture dynamics, no answers have ever been given to the question that to what extent wind can reduce the two times. Drying processes of fuelbeds composed of Korean pine needles were observed under nearly constant temperature and humidity but varied wind speeds. The two times of the processes were measured and effects of wind speed on the times investigated. Results show that under nearly 20℃ and 25%-30% humidity conditions, wind speed, fuelbed compactness and their interaction all have in fl uences on the fi rst time but not on the second time with benchmark set at fi re spread rate of fuelbed with moisture content of 0.3 g·g-1. Wind speed reduced the fi rst time by 1-1.3 h, nearly 40% of the time at zero wind speed condition. The relationship between the time and wind speed can be depicted by a exponential function. A fi tting function combining wind speed and fuelbed compactness was also established with satis fi ed accuracy.
wind speed; water loss time; moisture; Korean pine needle
S718.54+1
A
1673-923X(2016)12-0006-05
10.14067/j.cnki.1673-923x.2016.12.002
http: //qks.csuft.edu.cn
2016-01-17
国家大学生创新实验训练项目(201410225063);国家自然科学基金(31370656)
金 森,教授,博士;E-mail:jinsen2005@126.com
金 森,张俪斌,于宏洲,等. 风速对红松针叶床层两个重要失水时间的影响[J].中南林业科技大学学报,2016, 36(12): 6-10.
[本文编校:文凤鸣]

