基于TOA估计的超宽带快速定位方法
杨小凤,陈铁军,陈宇宁
(玉林师范学院 电子与通信工程学院, 广西 玉林 537000)
·信号处理·
基于TOA估计的超宽带快速定位方法
杨小凤,陈铁军,陈宇宁
(玉林师范学院 电子与通信工程学院, 广西 玉林 537000)
提出一种基于波达时间估计的脉冲超宽带定位方法,能够以较低的复杂度准确定位目标。文中算法利用功率时延谱对时间的一次导数构造多项式,把功率时延谱中搜索峰值的问题转化为多项式求根,可以降低搜索功率时延谱最大峰值的复杂度。由于该算法处理的是频域信号,文中设计了一种新型接收机模型,能够输出接收信号的等效频域采样值,而且能大大降低系统对ADC高采样速率的要求。Matlab仿真实验证明,该方法的TOA估计精度达到0.1 ns,定位精度达到厘米级,同时又易于工程实现。
脉冲超宽带;定位;波达时间;多项式求根
0 引 言
超宽带(UWB)信号是指绝对带宽大于500 MHz或相对带宽大于20%的无线信号,脉冲宽度可达到纳秒级,因此具有极高的时间分辨率,近年来被广泛应用于定位、雷达、追踪、传感网络等领域,具有定位精度高、功耗低、抗干扰性能强、安全性高等特点[1]。对于应用在一些恶劣和特殊的环境(如战争,地震,偏远山区等)中的无线网络,由于存在资源有限的特点,其定位机制必须满足低复杂度的要求;在追踪等应用场合中定位实时性也是非常重要的指标。在保证一定定位精度的条件下提高定位系统的实时性,即降低算法复杂度,降低系统对ADC高采样速率的要求,这是当前UWB定位技术的研究热点之一[2-3]。目前大多数UWB定位系统采用的是波达时间(TOA)定位法,其关键任务是精确估计首径信号的传播时延。近年来,国内外关于UWB快速定位技术的研究非常活跃,并取得了许多有价值的研究成果。文献[4]提出了一种基于最大似然估计准则和峰值检测的TOA估计算法,接收机采样速率为码元速率,但是需要使用多种码元,而且信号波形的设计对估计精度影响较大;文献[5]提出了两种基于贝叶斯估计准则的TOA估计算法,适用于能量检测接收机[6],采样速率为Sub-Nyquist速率,估计精度受复杂多径环境以及噪声的影响较大;文献[7]提出了一种基于阈值搜索的TOA估计算法,并设计了相应的接收机模型,采样速率为MHz级别,估计精度与设定的检测阈值密切相关。
首径信号的传播时延一般可以通过在功率时延谱中搜索最大峰值得到。本文提出一种新颖的TOA估计算法,把功率时延谱中搜索峰值的问题转化为多项式求根,可以降低搜索功率时延谱最大峰值的复杂度。由于算法处理的信号为频域信号,本文设计了相应的接收机模型,能产生接收信号的等效频域采样样本, ADC采样速率为Sub-Nyquist速率,从而降低了系统复杂度。Matlab仿真实验证明了该定位方法的有效性和可行性。
1 信号模型
待定位目标发射的脉冲超宽带信号(IR-UWB)s(t)由周期性重复的高斯脉冲一阶导数p(t)组成
(1)
设具有L条路径的多径衰落信道模型的信道冲激响应为[8]
(2)
式中:hl和τl分别为第l条路径的衰落系数和时延。
则接收信号为
r(t)= s(t)*h(t)+v(t)=
(3)
式中:v(t)为加性高斯白噪声。
将r(t)在时域采样后进行N点离散傅里叶变换(DFT)
(4)
式中:R(n)、S(n)、V(n)分别为接收信号,发射信号和噪声的DFT值;0≤n≤N-1。
将式(4)写成矩阵的形式
R=SEH+V
(5)
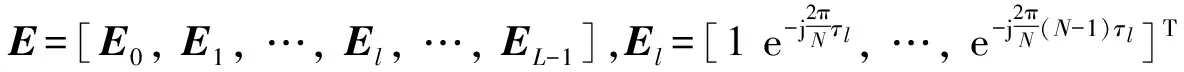
2 TOA估计——多项式求根法
功率时延谱(PDP),定义为信号能量随多径传播时延的分布[9],可通过式(6)计算得到
(6)
式中:Y=E[RRH]为频域接收信号的自相关矩阵。
首径传播时延的位置一般可以通过在功率时延谱中搜索最大峰值得到(功率时延谱峰值法),搜索复杂度(搜索次数)与搜索时延范围和搜索步长的比值成正比。本文提出一种新颖的多项式求根法,可以降低搜索功率时延谱最大峰值的复杂度。
根据矩阵的迹的性质[10],式(6)可改写为
(7)
式中:tr为求迹运算;Ypq为Y第p行、第q列上的元素。则在功率时延谱中搜索峰值的问题可转化为求式(7)的一次导数的根
(8)
(9)
式中:Ym为Y第m条对角线上的元素之和。式(9)为关于x的多项式。
功率时延谱式(6)可以改写为以x为变量的形式
(10)
其中
Ex=[1 x … xN-1]T
式(9)的2N-2个根中相角为负数的根对应功率时延谱的极大值和极小值,再求这些极大值和极小值中的最大值对应的根xo,通过式(11)求出首径传播时延
(11)
式中:angle为求相角运算。
至此,将基于多项式求根法的TOA估计的主要步骤总结如下:
1)求频域接收信号的自相关矩阵Y;

3)求该多项式的相角为负数的根;
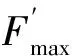
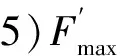
下面进行算法复杂度分析。以实现算法的过程中使用的实数乘法运算的个数(NOM)作为算法复杂度的度量,每次复数乘法运算相当于4次实数乘法运算。多项式求根法的NOM主要集中在求频域接收信号的自相关矩阵YN×N(N为DFT变换的点数)、多项式求根和求这些根对应的功率时延谱值这三步,运算量分别NOMA,NOMB及NOMC
NOMA=4N2+N2=5N2
(12)
(13)
NOMC=4(N2+N)·(2N-2)=8N3-8N
(14)
将以上三式相加,得到多项式求根法的NOM为
(15)
而功率时延谱峰值法的NOM与搜索时延范围τmax和搜索步长Δτ的比值成正比
(16)
设N=8,τmax=100 ns,Δτ=0.1 ns,代入式(15)和式(16),得到功率时延谱峰值法的NOM为2.88×105,多项式求根法的NOM为2.99×104,比功率时延谱的运算量少了一个数量级。
3 仿真实验
采用Matlab仿真实验验证本文算法的优越性。仿真中采用的高斯脉冲一阶导数p(t)的脉冲形成因子σ=0.15 ns;发射信号的脉冲重复周期T=5 ns,单脉冲的能量E=1J;信道模型采用IEEE 802.15.4a 标准[11]的CM1视距(Residential——LOS) 模型和CM2非视距(Residential——NLOS)模型,对两种模型分别产生100次独立的信道实现,用功率时延谱峰值法和多项式求根法进行TOA估计实验,得到估计精度——均方根误差(RMSE)和信噪比(SNR)的关系图如图1和图2所示。从图中可以看出,两种算法在视距环境下的估计精度均比非视距环境下的估计精度高,两种算法的估计精度均随SNR的增大而提高。在两种信道模型下,多项式求根法的估计精度均比功率时延谱峰值法高;SNR大于0 dB时,多项式求根法的估计精度达到0.1 ns。该仿真实验验证了多项式求根法良好的TOA估计性能。
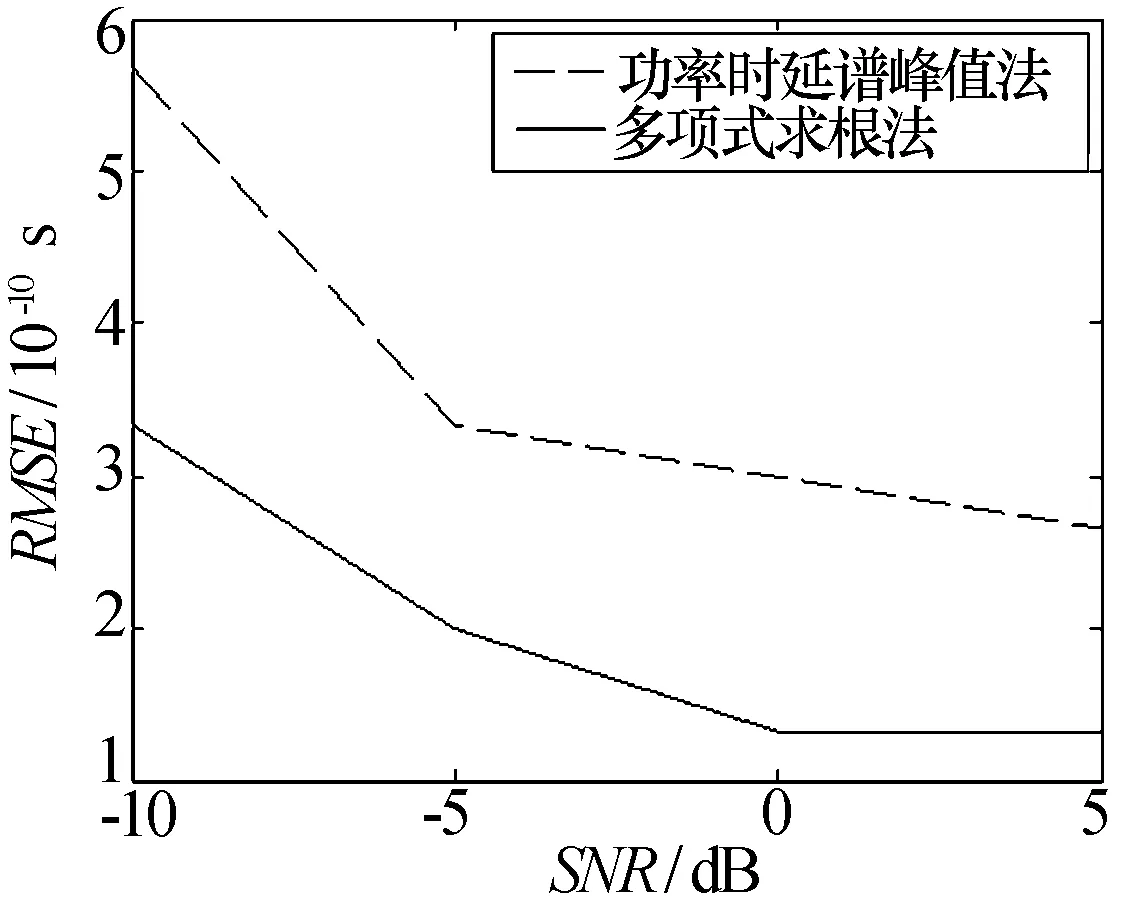
图1 CM1模型下TOA估计精度比较
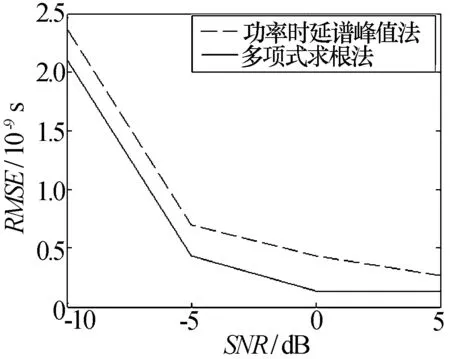
图2 CM2模型下TOA估计精度比较

(17)
(18)

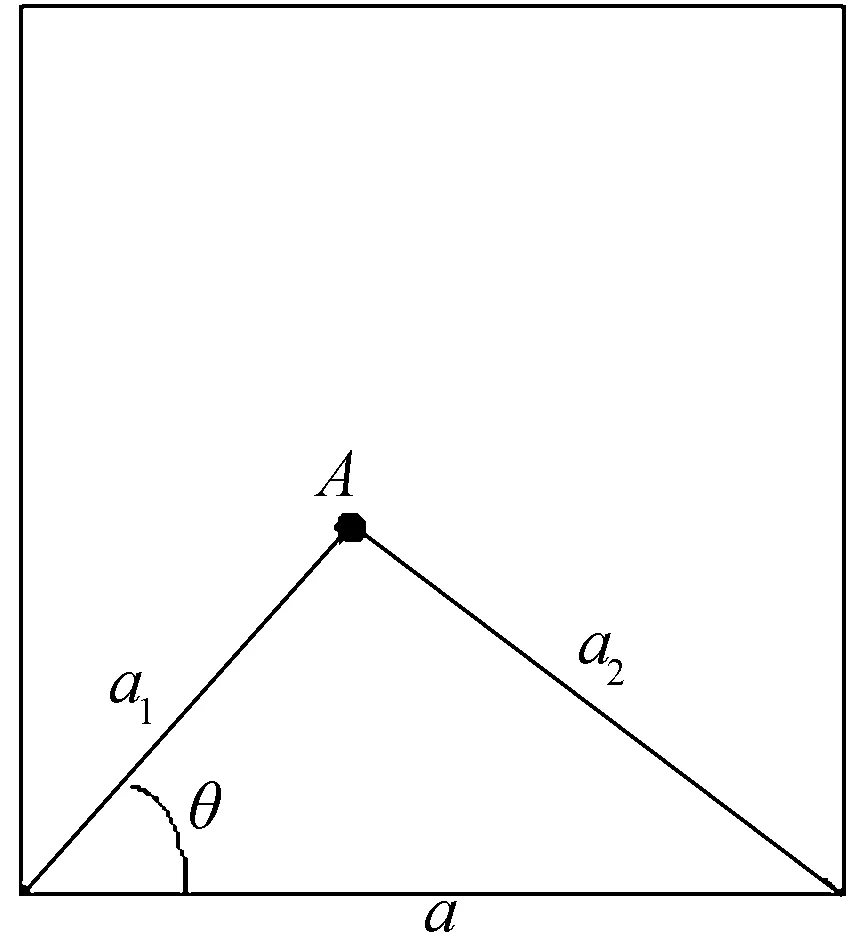
图3 定位实验场景

图4 多项式求根法的定位精度
4 接收机模型
UWB信号的带宽一般在GHz级别,所以在时域对UWB信号进行检测处理的一般接收机需要GHz甚至更高采样速率的ADC,造成系统硬件成本很高,功耗也非常大。本文算法处理的信号模型为频域信号,相应地本文设计了如图5所示的接收机模型,能够产生接收信号的等效频域采样值,而且能大大降低系统对ADC采样速率的要求,从而降低了系统复杂度。

图5 接收机模型
接收机模型由天线、放大器、功率分配器、滤波器组、下变频器、ADC和DSP等主要模块构成。带宽为Bw的接收信号r(t)被功率分配器分为B路,再经过带宽为Bw/B,冲激响应为式(19)所示 的滤波器滤波,然后由采样时间周期为T的ADC采样,每路输出信号可用式(20)表示。从该式可以看出,滤波器和ADC的处理相当于对接收信号进行了B路短时傅里叶变换[12],即得到接收信号的B路频域采样样本。而且由于每路信号的带宽为原始信号带宽的1/B,因此每路ADC的采样速率也下降为原始信号时域采样速率的1/B。
(19)
式中:g(t)为窗函数,通常为矩形脉冲函数(偶函数),因此有g(t)=g(-t)
(20)
当窗函数为矩形脉冲函数时,Ib(t-nT)为接收信号矢量空间的标准正交基[12],因此接收信号可以由其B路频域采样样本重构
(21)
5 结束语
本文提出一种基于波达时间估计的脉冲超宽带定位方法,利用功率时延谱对时间的一次导数构造多项式,把功率时延谱中搜索峰值的问题转化为多项式求根,可以降低搜索功率时延谱最大峰值的复杂度。本文还设计了相应的接收机模型,能产生接收信号的等效频域采样样本供算法处理,ADC采样速率为Sub-Nyquist速率,从而降低了系统复杂度。Matlab仿真实验证明了这是一种简单可行的定位方法。
[1] BHARADWAJ R, PARINI C, ALOMAINY A. Ultra wideband based 3D localization using compact base station configurations[J]. IEEE Antennas and Wireless Propagation Letters, 2014(13): 221-224.
[2] 肖 竹,王勇超,田 斌,等. 超宽带定位研究与应用:回顾和展望[J]. 电子学报,2011,39(1):133-141. XIAO Zhu, WANG Yongchao,TIAN Bin, et al. Development and prospect of ultra-wideband localization research and application[J]. Acta Electronica Sinica, 2011,39(1):133-141.
[3] NAVARRO M, NAJAR M. Frequency domain joint TOA and DOA estimation in IR-UWB[J]. IEEE Transactions on Wireless Communications, 2011, 10(10): 1-11.
[4] FALSI C, DARDARI D, MUCCHI L, et al. Time of arrival estimation for UWB localizers in realistic environments[J]. Eurasip Journal on Advances in Signal Processing, 2006, 2006(2): 1-14.
[5] YOUSSEF J, DENIS B, GODIN C, et al. New TOA estimators within energy-based receivers under realistic UWB channel statistics[J]. IEEE Vehicular Technology Conference, Taipei, 2010, 45(2): 1-5.
[6] GUVENC I, SAHINOGLU Z, ORLIK P. TOA estimation for IR-UWB systems with different transceiver types[J]. IEEE Transactions on Microwave Theory and Techniques, 2006, 54(4): 1876-1886.
[7] BELLUSCI G, JANSSEN G, YAN J L, et al. Performance evaluation of a low-complexity receiver concept for TOA-based ultra wideband ranging[J]. IEEE Transactions on Vehicular Technology, 2012, 61(9): 3825-3837.
[8] FANG S, CHAMPAGNE B, PSAROMILIGKOS I. Joint estimation of time-of-arrival and channel power delay profile for pulse-based UWB systems[J]. IEEE International Conference on Communications, 2012, 11(18): 4515-4519.
[9] 杨鸿文,李卫东,郭文彬,等. 无线通信[M]. 北京:人民邮电出版社,2012:72-73. YANG Hongwen, LI Weidong, GUO Wenbin, et al. Wireless communications[M]. Beijing: Posts and Telecom Press, 2012:72-73.
[10] 张贤达. 矩阵分析与应用[M]. 2版. 北京:清华大学出版社,2013. ZHANG Xianda. Matrix analysis and application[M]. 2nd ed. Beijing: Tsinghua University Press, 2013.
[11] MOLISCH A, BALAKRISHNAN K, CHONG C C, et al. IEEE 802.13.4a channel model-final report[S]. 2005.
[12] 余翔宇. 数字信号处理:基于计算机的方法[M]. 4版. 北京:电子工业出版社, 2012: 173-175. YU Xiangyu. Digital signal processing: with methods based on computer[M]. 4th ed. Beijing: Publishing House of Electronics Industry, 2012: 173-175.
杨小凤 女,1984年生,讲师。研究方向为超宽带无线定位,阵列信号处理算法及其应用等。
陈铁军 男,1966年生,教授。研究方向为无线网络。
陈宇宁 男,1976年生,讲师。研究方向为电子技术。
A Fast UWB Positioning Method Based on TOA Estimation
YANG Xiaofeng,CHEN Tiejun,CHEN Yuning
(College of Electronics and Communications Engineering,Yulin Normal University, Yulin 537000, China)
This paper proposes a novel positioning method based on time-of-arrival (TOA) estimation for impose ultra-wideband systems, which can locate targets with high accuracy and low complexity. The algorithm derives a polynomial from the first derivative of power delay profile and finding the maximum points of the power delay profile is equivalent to calculate the roots of the polynomial, thus reducing the search complexity. Since the algorithm is a frequency domain approach, this paper also designs corresponding receiver model which outputs equivalent signal samples in frequency domain and reduces the high demand on ADC sampling rate. Matlab simulation results prove that this method achieves TOA estimation accuracy of 0.1 ns, which leads to centimeter-order of positioning accuracy while it is easy for implementation.
IR-UWB; positioning; TOA; solving polynomial
10.16592/ j.cnki.1004-7859.2016.03.006
广西高校科学技术研究项目(KY2015YB240);广西高校科学技术研究重点项目(2013ZD055)
杨小凤 Email:yy2822205@163.com
2015-10-26
2015-12-28
TN911.7
A
1004-7859(2016)03-0028-04

