径向进气室对叶轮性能影响的数值研究

冯占宸 高阳 宋茜/沈阳鼓风机集团股份有限公司

径向进气室对叶轮性能影响的数值研究

冯占宸 高阳 宋茜/沈阳鼓风机集团股份有限公司

0 引言

离心压缩机各元件之间的相互匹配关系，已经成为近些年叶轮机械研究领域的热点之一。在离心压缩机中，管路来流经过进气室进入首级，因此进气室出口的流动情况会直接影响压缩机首级的性能。对于一个典型的离心压缩机级，进气室和蜗壳流动损失产生的效率降低约为4％～6％[1]。相比于其它进气室结构，径向进气室因为具有结构紧凑的优点，所以被广泛应用在多级压缩机组中。然而与此同时，由于径向进气室具有几何结构非轴对称、收敛通道处气流折转等特性，因此其内部流动复杂、出口气流分布存在畸变，这些现象不仅使得进气室本身损失增加，还会导致叶轮偏离轴向进气假设下的预期性能。

近年来，随着CFD技术的快速发展，国内学者采用数值手段进行了大量的径向进气室相关研究。陈宗华等[2]采用基于CFD技术的数值优化方法，通过改进气室结构，提升了压缩机的首级性能。董帆等[3]对比了径向进气室与轴向进气室对压缩机外特性及内部流动的影响，发现径向进气室会影响叶轮进口流动的均匀性，降低级效率和总压比，同时，叶轮对进气室也有影响，使得其内部流动不对称。龙峰等[4]的研究显示，与轴向进气室相比，径向进气室会引起效率和压比的下降，径向进气室出口流动存在不均匀性，且该处流动受叶轮影响明显。王锐等[5]通过采用分流叶片结构，减少了径向进气室出口气流的畸变，改善了叶轮叶片受力和压缩机性能。王锐等[6]详细给出了进气室内部的流动结构，结果显示，流动损失和进气室出口的畸变主要是由于气流在环形通道中产生的旋涡造成的。

本文采用数值模拟方法，对比两个径向进气室设计方案对压缩机首级叶轮性能的影响，分析了其内部流动情况，并且比较进气室单独计算的结果与进气室-叶轮耦合的结果，以探究耦合作用对进气室流场产生的影响。

1 计算模型及计算方法

1.1 计算模型及网格

本文的研究对象由进气室、闭式叶轮和出口无叶段组成。为了减少计算耗时以及提高计算的鲁棒性，本文的计算域并未包含叶片扩压器与回流器等下游原件。因此在不改变子午视图布置的基础上，设计了两个进气室方案，分别为算例G0与G1。离心压缩机模型级在设计过程中，均按照轴向进气设计，即文中的0-2截面轴向进气算例。而在实际应用中，需要加入径向进气室。这就导致了首级性能与理想轴向进气时不同。本文研究进气室对首级性能的影响，比较轴向进气（0-2），与带进气室径向进气（in-2）的性能。此外，为了进行比较，本文还包含了叶轮轴向进气的算例I。具体几何结构如图1所示。

图1 计算模型几何结构示意图

本文采用NUMECA软件的IGG和Aurogrid5模块分别制作了结构化的进气室与叶轮通流部分网格。当叶轮进口为轴向进气时，采用单通道网格进行计算，计算域为0截面到2截面；当叶轮与进气室网格进行耦合计算时，叶轮采用全通道网格，叶轮与进气室之间采用转静子交接面完成数据传递，计算域为in截面到2截面。叶轮与进气室壁面网格宽度分别取0.005mm与0.01mm，保证壁面Y+≤10。计算域网格如图2所示。

图2 进气室与叶轮拼接算例计算域网格图

1.2 计算方法及边界条件

本文采用商业CFD软件NUMECA作为求解工具，采用时间推进法求解流动控制方程组，选取S-A湍流模型封闭N-S方程。数值方法上应用二阶中心差分格式，采用多节点并行计算、多重网格和隐式残差光顺等技术加速收敛。计算收敛标准为进出口质量相对误差下降到0.5％以内，总体残差降到10-5，效率和压比保持恒定。

边界条件方面，将压缩机组的实际进气条件，在保证首级叶轮马赫数、流量系数相同的前提下，转换为常温常压进气。介质采用假定的理想气体，其物性随温度压力保持不变，物性参数由实际混合气体在常温常压下计算获得。进口给定总压、总温，气流无预旋，出口给定质量流量，固体壁面给定无滑移和绝热条件。当叶轮与进气室耦合计算时，采用冻结转子法完成数据传递。注意，本文将进气室视作叶轮进口结构的一部分，因此轴向进气与径向进气的进口边界条件相同。

2 计算结果

2.1 性能比较

选取轴向进气时的叶轮最高效率工况点进行性能比较，该工况Mu=0.42，出口质量流量为2.75kg/s。计算结果如表1所示。其中算例G0与G1的效率与压比采用in-in截面、2-2截面的参数计算获得，总压损失系数采用in-in截面、0-0截面参数计算获得。

相比于轴向均匀进气的算例I，G0与G1算例的多变效率分别降低了21.4％与2.8％，首级叶轮产生的总压压比分别降低了0.052与0.003。由此可以看出虽然使用了同样的叶轮，但是采用不同的进气结构，压缩机首级叶轮所表现出的性能差别极大，算例G1的进气室性能上明显优于G0。比较两者的总压损失系数可以发现，算例G0的进气室总压损失较大，这也是造成G0算例性能低的原因之一。

表1 叶轮最高效率点性能比较表

2.2 内部流场分析

2.2.1 叶轮进口截面（0截面）

0截面的流动情况会直接影响叶轮内部流动，因此该截面上流动的均匀性、偏离轴向流动的程度至关重要。图3显示了各算例的0截面静压、马赫数以及切向气流角分布云图。

图3 0截面静压、绝对马赫数与切向气流角分布云图

从0截面静压云图可以看出，G0算例的0截面静压分布最不均匀，存在局部高压与低压区，在同一半径上沿周向压力变化较大。G1算例尽管同样存在着相对的高压与低压区，但变化范围远小于G0算例，此外，从等值线上可以看出压力沿圆周方向的均匀程度要优于G0算例。G0与G1算例的马赫数云图显示出位于底部的高速区，这主要是由于进风筒位于进气室的下方，下部气流流经线路短，流速高。与G1相比，G0算例的流速畸变现象要更加严重，高速区的数值更大。类似地，切向气流角云图也显示出相似的趋势，G1算例的切向气流角分布更接近于算例I。

综上，可以看出径向进气室对叶轮进口流场的影响明显，与轴向进气算例I相比，G0与G1均存在不同程度的畸变。叶轮在进行气动设计时，通常基于轴向无预旋假设，因此叶轮进口流动的畸变，必定改变局部的叶片前缘气流冲角，造成效率降低。相比较而言，G1的均匀程度要好于G0，流动也更接近轴向进气，这也是G1的外特性优于G0的原因之一。

2.2.2 进气室内流动

0截面的流动受上游环形通道、进风筒结构影响，因此进气室内部的流动也是压缩机设计者关注的重点。G0与G1的进气室主要存在两点结构区别：G1进风筒出口面积大于G0；G1进气室顶部增加了“眉毛”结构，取消分流筋。图4展示了G0与G1算例在A-A截面的绝对马赫数云图、流线图。

对比马赫数云图可以看出，G0算例因为进风筒进口面积过小，导致进风筒下游流速高于周向其他部位，局部最高绝对马赫数达到了0.316。观察G0的流线可以明显看到在低马赫数区存在着大量旋涡，其位置分别位于进风筒出口两侧与分流筋板两侧，并与总压数值较低的区域相重合。大量旋涡的存在不仅影响了进气室出口流动的均匀性，也造成进气室本身总压损失系数较高。

观察G1的马赫数云图可以发现其最高马赫数只有0.113左右，与周向其他部位流速相差不大。在“眉毛”部位也存在一定的低速区，但是通过观察流线图可以看到流动在该部位并未形成旋涡，流线平顺的进入下游区域，该区域产生的总压损失也要小于G0算例。从本文的规律可以看出增大进风筒的出口面积，有利于降低总压损失、产生均匀的出口流动，但进风筒出口面积过大会引起机壳等零件的强度问题，因此应当综合考虑。

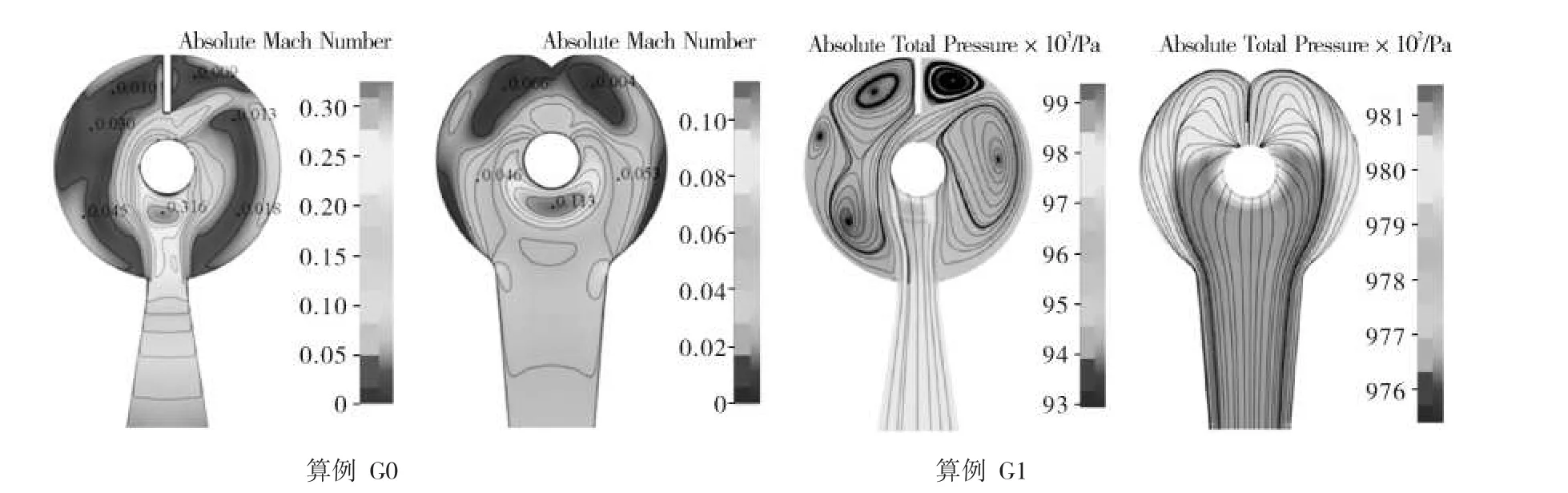
图4 马赫数云图与流线图（总压云图）

2.2.3 单独进气室内部流动

进气室与叶轮之间的相互耦合作用，不仅表现在进气室对叶轮内流场产生影响，而且叶轮的存在也会影响进气室内的流动。为了探究叶轮对进气室的影响，本文对G0与G1两个算例的进气室部分进行了单独的数值计算。为了保证内部流动稳定、充分发展，计算域在进口与出口方向进行了一定的延长，边界条件与耦合算例相同。单独计算结果的0截面切向气流角分布云图与A-A截面流线图如图5所示。

图5 切向气流角云图（0截面）与流线-总压云图（A-A截面）

将图5中的切向气流角分布云图与图3比较，发现耦合计算与单独计算的区别较大，单独计算进气室获得的0截面切向气流角最大值要小于耦合计算的结果，而且切向气流角的分布也更加均匀。造成这一差异的原因，是叶轮旋转带动0截面附近流场随之转动，增加了0截面流动的不均匀性。比较G0与G1的进气室单独计算结果，发现G1切向气流角分布的均匀性仍远好于G0。

比较图5与图4的流线图可以发现，耦合作用对流线、总压分布的影响并不大，流线形状基本相同。值得注意的是，G1算例在单独计算时“眉毛”处出现了回流区，这在耦合计算中并未出现。出现这一现象的原因可能是叶轮进口的“吸气”效果，有助于进气室内的气流稳定流入收敛通道。

综上比较发现，进气室单独进行数值计算，可以在一定程度上反应进气室的优劣，但是进气室内部流场受叶轮耦合作用的影响显著。

3 结论

本文采用NUMECA软件对具有不同进气结构的压缩机首级叶轮进行了数值研究，得到以下结论：

1）径向进气室的存在会在叶轮进口造成流动的畸变，使得进入叶轮的流动不均匀。此外，径向进气室本身会产生一定的压力损失。这些效应综合在一起，会导致首级叶轮效率、压比的下降。

2）径向进气室的几何结构会影响进气室内的流动以致影响首级叶轮的性能。增加进风筒出口面积，有助于改善进气室内流动，获得均匀叶轮进口流场；“眉毛”结构有助于消除进气室上部的回流区域。

3）下游叶轮对径向进气室内的流动同样会产生影响，造成进气室内部流动、进气室出口气流分布发生变化。

4）单独分析进气室内部的流动情况，能够在一定程度上反应进气室设计的优劣。

[1]Engeda A,Kim Y,Aungier R,et al.The inlet flow structure of a centrifugal compressor stage and its influence on the compressor performance[J].ASME Journal of Fluids Engineering,2003,125 (3)：779-785.

[2]陈宗华，谷传纲，舒信伟.基于CFD技术的离心压缩机径向进气室结构形状优化设计[J].机械工程学报,2010,46(14): 124-129.

[3]董帆，于跃平，朱晓农.径向进气室对离心压缩机气动特性影响的研究[J].流体机械,2012,40(11):15-20.

[4]龙峰，谭佳健.径向吸气室对离心压缩机级性能的影响[J].风机技术,2010(2):7-11.

[5]王锐，祁大同，王学军，等.离心压缩机径向吸气室的流动损失分析和改进设计[J].应用力学学报，2009，26(3):437-443.

[6]王锐，祁大同，王学军，等.离心压缩机径向吸气室内部流动的数值研究[J].流体机械，2008，36(6):19-24.

■

在保证子午面结构不变的前提下，设计了两个径向进气室方案。采用CFD对径向进气室与首级叶轮进行了流场分析，并且与轴向进气方案进行了比较。结果显示，径向进气室会造成叶轮进口流动的畸变，导致首级叶轮的效率和压比下降；同时，径向进气室的性能与几何形状关系密切。

径向进气室；离心压缩机；几何结构；数值模拟

Numerical Simulation Research of the Im pactofRadial InletChambers on the Performance of Impellers

Feng Zhan-chen，Gao Yang，Song Qian/ Shenyang BlowerWorksGroup Co.,Ltd.

Abstract：Two radial inlet chamber are designed to ensure the meridian plane structure is unchangeable.The flow field of the radial inlet volute and first stage impeller was analyzed with CFD，and was then compared to the case of axial air inflow design.The results indicated that radial inlet chambers can cause flow distortions in the impeller's inlet，that will decrease efficiency and first stage impeller pressure ratio.Meanwhile,it proved that the performance of radial chambers have close relations togeometry shape.

radial inlet volute;centrifugal compressor;geometrical structure;numericalsimulation

TH452;TK05

A

1006-8155（2016）03-0037-05

10.16492/j.fjjs.2016.03.0018

2015-09-18辽宁沈阳110869