基于安全存货的EOQ模型及其应用

王嗣琦

南京航空航天大学金城学院，江苏南京，211156



基于安全存货的EOQ模型及其应用

王嗣琦

南京航空航天大学金城学院，江苏南京，211156

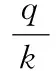
安全存货；经济批量；订货成本；储存成本

1 提出问题和相关研究

存货管理是现代企业短期资产管理的重要环节。特别是对存货占短期资产比重较高的生产型企业，存货利用效率对企业财务状况的影响较大[1]。企业存货过多，不仅会占用企业大量流动资金，也会增加企业仓储成本；存货不足，可能面临生产缺货、影响销售、有损商家信誉，增加企业经营风险等。因此，确定合适的订货量，使存货保持在最优水平，既可以保持企业运作的经济性，如适量的订货量既可以获得供应商提供的商业折扣，又可降低运输成本；既可以有效地调节供需平衡，缓解需求波动带来的矛盾，又可以缓解企业经营风险[2]。

1915年，哈里斯(F.W.Harries)在研究企业库存问题时首次提出EOQ模式[3]；1935年，威尔逊(R.H.Wilson)在研究同类问题时采用不同的方法也得到与哈里斯相同的结论，即所谓传统EOQ模型(经济批量模型)或威尔逊(Wilson)公式[3]。此后，随着供应链管理的发展，传统EOQ模型在制造、贸易、物流企业得以广泛使用。

在传统经济批量模型理论的基础上，许多学者提出的存货模型都是在确定环境条件下得到的，且模型的提出与推导并没有全面考虑现实环境变化可能产生的影响。特别是被广泛认可的经典的EOQ模型，因有严苛的假设，在企业生产、经营、管理的现实应用中受到了较大的限制。从经济订货批量的研究内容看，很多学者或是从EOQ模型假设入手，逐步放宽假设条件，对EOQ模型加以改进[4-7]；或是从调整部分环境变化入手，推导不确定环境中的优化存货模型[8-11]。

李温红在研究了需求确定、不允许缺货、瞬时供货且库存容量有限的条件下，给出租借仓库的最优存贮模型[4]：

刘德权在研究了需求确定、允许缺货、瞬时供货且库存容量有限条件下，同样给出了租借仓库的最优存储模型[5]：

杨益民在研究了需求确定、不允许缺货、生产有一定时间要求且库存容量有限的情况下，给出租借仓库的最优存储模型[6]：

刘斌在刘德权研究的基础上，假定生产需要一定时间或在杨益民研究的基础上，假定允许缺货并产生缺货损失，给出更一般的最优生产批量模型:

据此可以考察企业在需求确定、库存容量有限时的订货行为[3]。

谢海娟、陶晓美对传统经济订货批量模型进行了修订，她们认为在允许缺货、有数量折扣且陆续到货时，相关总成本为[7]：

Park将EOQ模型的订单和库存成本作为梯形模糊数，对经济订货批量进行了求解[8]。Roy和Maiti提出了一个模糊的EOQ模型与有限的存储容量，并在目标函数和存储区域都引入了模型的模糊性[9]。Samanta和Al-Araimi开发了一个基于模糊逻辑的存货模型，考虑了可变订单数量的存货控制周期性回顾模型[10]。李群霞、李争香在模糊环境下采用阶梯模糊数来描述现实生产环境，对不允许缺货、全部要素均为模糊数时的EOQ模型进行优化求解，确定经济订货批量[11]。

还有一些学者从供应链环境下采购价格折扣和库存成本的敏感性等方面对传统EOQ模型进行修正，如郭晓霞、闫学峰从EOQ模型的敏感性、单位订购费用与单位库存保管费不确定性的角度，将库存成本、采购价格折扣引入传统EOQ模型，使其更具实践意义[12]。

从模型研究方法看，大多数学者在进行最优经济批量的推导中利用微分求极值的方法，少数学者使用代数或线性规划法进行推导。从研究的内容上看，多数研究都是从模型的假设入手，将假设的数量或者内容进行调整，使模型更具一般性，进而在更符合现实情况下探讨最优经济订购(生产)批量、成本最小化以及企业利润最大化问题。

本文在假定企业考虑安全存货的条件下，采用微分求极值法，对传统EOQ模型进行改进，使其更符合现代企业生产、经营、管理的实际。

2 传统EOQ模型分析

传统EOQ模型通过确保一定时期内总储存成本和总订货成本之和最小来确定经济批量。通过对哈里斯和威尔逊构建传统EOQ模型提出的假设分析可知，要利用传统EOQ模型确定最优经济批量，企业的生产或销售活动需满足如下五个基本条件：(1)一定时期内企业对某种存货需求D确定不变；(2)一定时期内企业单位批次订货成本C0和订货量不变；(3)一定时期内企业对某种存货的单位储存成本Cs不变；(4)一定时期内企业对某种存货的消耗是均匀的；(5)当企业某种存货降为零时，企业存货可以瞬时得到补充，不会出现生产停工待料或销售缺货的现象。其中，订货成本与储存成本呈反向变动关系，订货批量越大，企业储存的存货就越多，进而使总储存成本上升；此时订货次数减少，总订货成本降低。反之，订货批量减少能够降低储存成本，但由于订货次数增加，总订货成本会上升。

据此，可得传统经济订货批量公式：

(1)

显然，在企业实际应用传统EOQ模型时，只要有一个条件不能满足，就理论而言，则不能采用其确定最优经济订购(生产)批量。事实上，在现代企业的生产、经营、管理中，几乎不可能同时满足以上五个条件。因此，采用传统EOQ模型确定企业最优经济批量、最优订货批次、最小存货成本，难以实现企业存货管理的预期目的。

另外，在上述五个条件下确定的最优经济批量，可以看作是企业年存货需求量、单位订货成本、单位储存成本的三元非线性函数。事实上，现代企业的存货管理成本并非只受到这三个方面的影响，还包很多因素。就企业对某种原材料或商品的年需求而言，除受到价格、质量、自身需求弹性大小等因素影响外，还受到消费者的消费偏好、可支配收入等外部因素影响。也就是说，一定时期内企业对某种原材料或商品的年需求量往往不是确定不变的。同样，受现代运输方式、物流方式、供货商经营行为等因素影响，企业对某种原材料或商品的年需求量也在发生变化，从而直接或间接地影响企业最优经济批量的确定。

从建立传统EOQ模型的条件(4)看，其本质在于企业前后两批原材料或商品到货之间，企业原材料或商品存货的消耗量必须服从或近似服从均匀分布。显然，这在企业生产、经营和管理实践中无法实现。因为市场经济条件下，企业产品销售量取决于消费者的消费需求和购买力，尽管企业可通过加快或减缓生产进度来控制一定时期内原材料的消耗量，但实践中大多数企业的生产计划往往视产品的销售状况而定。如果产品销售需求增加，则增加产品生产，从而使原材料的消耗加快；反之，减少产品生产，则使原材料的消耗减缓。因此，在一定时期内，企业对某种原材料或商品存货的消耗难以服从或近似服从均匀分布。

从建立传统EOQ模型的条件(5)看，其本质在于当企业上一批次所采购的原材料或商品耗尽或售罄时，后一批次订购的原材料或商品正好在当日运达并由企业验收入库以备使用。这样，企业生产或销售不会出现缺货现象，即具有“瞬时到货”的特征。显然，这也只是一种较为理想的假定。尽管有些现代企业采取JIT存货管理模式，但该模式对企业的供应链管理要求极高，企业为建立非常稳定的供应链，往往会支付较高的“维护”成本。因此，许多企业为防止缺货、断货，通常保留一定数量的存货即安全存货，这样更可靠。

事实上，无论何种模型，模型的前提假设越严格就越理想化，与实践差距就越大，模型的使用就越缺乏准确性和参考性；模型假设越少或设定的条件越宽松，与实践情况越相近，模型才能更好地模拟实践。传统EOQ模型的缺陷主要在于模型设定条件过于严格，这样限制了模型的实际应用。

3 基于安全存货的EOQ模型构建

在现代企业生产、经营和管理活动中，为了降低生产出现停工待料或商品销售缺货现象发生的概率，多数企业均会考虑持有一定数量的安全存货，以减少相应的经济或信誉损失。因此，笔者在保持传统EOQ模型前四个条件不变时，将最后一个条件放宽，即在企业考虑持有一定安全存货的情况下，采用导数求极值的方法确定最优经济批量。

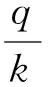
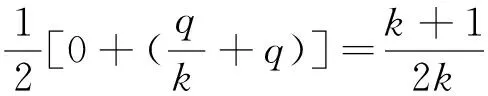
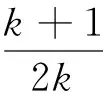
由 TC=TCo+TCs

(2)

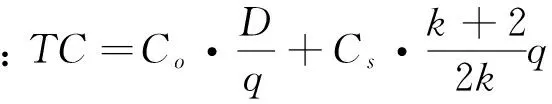
(3)

(4)

(5)

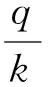
4 基于安全存货的EOQ模型应用

与传统EOQ模型相比，利用基于安全存货的EOQ模型可以更科学地帮助企业确定最优经济订购批量，降低企业运营成本，提高企业资本运作效率，使企业在行业竞争中更具优势。

一是用于确定企业一定时期最优经济订购批量。事实上，尽管持有安全存货会增加企业的储存成本，但大多数企业为了防止生产经营过程中存货耗用异常或存货供应不足而影响生产或经营的连续性，都会持有一定量的原材料或商品作为安全存货。据此可以测算其最优经济订购批量：

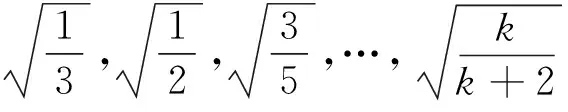
二是用于确定企业一定时期最优经济订购批次。若企业决定采用安全存货管理模式，可先根据模型(5)确定最优经济订购批量，进而再确定在一定时期内最优经济订购批次：

(6)

据此，企业可以制定采购方案，协调采购和仓储管理工作，做好车辆运输协调以及货物的检测检验工作等。

三是用于确定企业一定时期最小存货管理成本，有助于降低企业总生产营运成本，实现利润最大化。根据(5)和(6)可测算出最小总成本：

(7)

据此，企业可以制定一定时期相关原材料或商品存货的订购计划，合理高效地安排企业资金的使用与周转。同时，也可以为企业生产管理部门的业务考核提供依据。

例如，2017年某生产企业预计需要消耗20000吨某种原料，根据历史经验每批次的订购成本是30元，每吨仓储成本是7元。假如安全存货是最优订货量的1/10、1/20、1/50、1/100，即当k分别为10、20、50和100时，利用式(5)可得最优订货量分别为378吨、395吨、406吨和410吨，相应的安全存货分别为37.8吨、19.75吨、8.12吨和4.10吨；利用式(6)可得最优订货批次分别为53次、51次、49次和49次；利用式(7)可得最小存货管理成本分别为2078元、1990元、1935元和1916元，比传统EOQ最小存货管理成本分别高出19.45%、4.88%、1.98%和1.00%。

显然，至于该企业实际会选择多少原料作为安全存货，这取决于企业现有的仓储容量、发生缺货可能带来的直接与间接的经济损失及其可能承担的最大存货管理成本。但是，根据模型参数k的每一个不同取值，则对应一个可供企业选择的方案。

5 结束语

本文通过考虑企业为降低停工待料或缺货发生的风险而普遍留有安全存货的现实情况，将传统的EOQ模型加以修正，得到了基于安全存货的EOQ模型公式，并证明了传统EOQ模型是修正模型的一种特殊情况。因而,更具一般性的基于安全存货的模型在实践中可以更加科学地帮助企业确定最优经济批量、最佳订购批次和存货管理成本。但是，本文仅是针对一个模型假设条件的修正，因此，基于安全存货的EOQ模型的成立仍然需要其他四个假设作为前提条件，与现实情况仍有一定差距。同时，修正模型在使用时需要企业根据自身具体情况来确定模型参数k，使得测算结果存有一定的主观性。

[1]荆新，王化成，刘俊彦.财务管理学[M].北京：中国人民大学出版社，2014：309-310

[2]陈斯瑜.基于库存价值变化和随机需求的经济订货批量模型研究[D].武汉：华中科技大学管理学院，2009:1-6

[3]刘斌，刘思峰，翟振杰.EOQ模型的一个注记[C]//第八届全国青年管理科学与系统科学学术会议论文集.南京：河海大学出版社，2005:377-379[4]李温红.仓库容量有限条件下的不允许缺货存贮模型[J].系统工程理论方法应用,1997,6(3):68-71

[5]刘德权，徐毓，孙知建.仓库容量有限条件下的缺货存贮模型[J].空军雷达学院学报，2002,16(1):22-23

[6]杨益民，付必胜.仓库容量有限条件下的生产销售存贮模型[J].系统工程，2001,19(1)：18-23

[7]谢海娟,陶晓美.存货经济订货批量模型研究[J].财会月刊，2010(11)：59-62

[8]K S Park.Fuzzy-set theoretic interpretation of economic order quantity[J].IEEE Transactions on Systems, Man and Cybernetics,1987,17(6):1082-1084

[9]T K Roy，M Maiti.A Fuzzy EOQ Model with Demand Dependent Unit Cost under Limited Storage Capacity[J].European Journal of Operational Research,1997,99(2):425-432

[10]B Samanta，S A Al-Araimi.An inventory control model using fuzzy logic[J].International Journal of Production Economics,2001,73(3):217-226

[11]李群霞,李争香.基于模糊集的经济订货批量模型的优化研究[J].中国管理信息化，2012(3)：59-60

[12]郭晓霞，闫学峰.供应链环境下库存管理EOQ模型分析及应用[C]//第三届不确定系统年会论文集.南京：2005：510-516

(责任编辑：周博)

2016-09-10

王嗣琦(1990-)，女，江苏南京人，硕士，助教，主要研究方向：企业财务管理。

10.3969/j.issn.1673-2006.2016.11.008

F

A