多机外场实弹保障装备配置优化方法研究

陈晔，韩强，王玉刚

（海军航空工程学院青岛校区，山东青岛266041）

多机外场实弹保障装备配置优化方法研究

陈晔，韩强，王玉刚

（海军航空工程学院青岛校区，山东青岛266041）

考虑了多机多武器实弹保障问题，以航炮、拦截导弹与格斗导弹的检测仪配置形式为例，将外挂物装挂前检查保障作业抽象成车间内自由作业，给出了保障设备配置方案的优化方法。根据保障约束条件与各项工作所需的时间，计算出设备的配置方案，用三元组简化排序问题的表示形式，将保障流程进行调整后用甘特图进行直观展现，并检验了优化后的配置方案。

多机组；实弹保障；装备配置；优化方法

0 前言

飞机执行任务，地面人员要对飞机进行保障，在进行单机保障的时候不存在保障设备优化的问题，但是在实际工作中，基本上都是要求多机同时执行任务，在多机保障的时候会出现保障设备利用率很低的情况，很多时候都是设备在等飞机，造成很大的浪费。如何科学合理配备保证装备数量并在有限的设备的基础上保证完成任务，提高设备利用率，是保障人员的面临难题。从保障装备配置优化方面入手，利用设备配备数量的计算公式和甘特图法，对多机实弹保障装备配置进行优化。

1 保障装备配备条件与作业要求

本文假定的保障方案为飞机装挂航炮、空空拦截导弹与空空格斗导弹，讨论的保障设备是这3种武器的检查仪，即航炮检查仪、拦截导弹检查仪以及格斗导弹检查仪。根据以往的保障装备配置方案，1个机组2架飞机配置1套检测仪器，虽然这样一定能保证在规定的时间内完成保障任务，保障人员也可以很容易的掌握保障情况和进度，但是检测仪器很多时候没有利用起来，设备的利用率很低，保障设备的价格往往很昂贵，如果设备利用不起来，这就造成了极大的浪费。

在实际的外场实弹保障过程中，保障的时间是有要求的，只要在规定的时间内把航炮或导弹按照武器悬挂方案挂到飞机上就算完成保障任务。在此设定武器悬挂方案，航炮、空空拦截导弹、空空格斗导弹，假设1架飞机各个武器的检测时间：航炮2 min、空空拦截导弹7.5 min、空空格斗导弹3 min。以1个机组2架飞机为基本单位，参考机组专业人员配置情况，1个机组的检测时间为航炮4 min、空空拦截导弹15 min、空空格斗导弹6 min。为了方便计算，将1个机组（2架飞机）相同武器的检测工作合并在一起进行，1个机组武器装挂的保障总时间取80 min。

2 多机检测流程优化理论依据

由于1个机组的3种武器的检测工作不能同时进行。这3种武器的保障的先后顺序没有严格的限制，即各项保障工作之间没有什么相关性，这就为多机实弹保障流程的优化提供了前提条件。多机实弹保障流程优化问题抽象出来，属于运筹学里的动态规划中的排序问题，进一步可以归纳为车间内自由顺序作业问题。

（1）车间内自由顺序作业问题。如果每个作业后任务需要在每个机器用来加工或处理，每一作业或任务加工的顺序可以自由选择，那么就称这种方式为自由顺序作业方式。在一定数量的加工机器或保障资源的限制下，最优地完成给定的作业或任务（最优完成通常指的是使加工时间最短，设备利用率最高等），这就是排序优化。在这一节中，最优的完成指是在规定时间内，使用有限数量的保障设备，完成保障任务，提高设备利用率。

（2）多机检测流程数学模型。用Graham等人首先使用的三元组（α|β|γ）来描述排序问题，可以大大简化排序问题的表示。典型自由顺序作业的三元组表示为式（1）。

式（1）中Om表示m个检测设备，工作方式是自由顺序作业方式；Cmax为完成所有该型飞机3项基本机务准备工作所需时间，即总完工时间T′，总完工时间越短说明装备利用率越高，P为各项任务加工时间矩阵，Pij表示第i个检测设备完成第j个任务所需的时间。

3 多机检测流程优化过程

假设要完成N个机组的3种武器的装挂前检测任务。根据上面给出的资料，可以得到各项检测工作所用时间分别为，航炮检测P1=4 min、空空拦截导弹检测P2=15 min、空空格斗导弹检测P3=6 min，检测装备分别是航炮检测仪（P1）、拦截导弹检测仪（P2）、格斗导弹检测仪（P3）。各项检测工作的转换时间在本文中忽略不计。进行检测机组为。Pij表示第i个检测设备完成第j个任务所需的时间。将数据带入（1）式见（2）式。

根据模型的适用范围，可将问题分为N＜m，N≥m的2种情况分别进行讨论，即3个机组（含3个）以上和3个机组以下2种情况，但2种情况均是无论采取何种优化方法飞机飞行前的3项准备工作时间，都无法少于单机准备时间或耗时最长的检测装备（拦截导弹检测）的总工作时间（15×N），其中N为保障机组的数量。

3.1 当保障3个以下机组（N＜m）的检测流程优化

当N=2＜m=3时，排序问题就失去一般性，可以直接利用最简单的并行工作方式给出保障流程的甘特图（图1）。

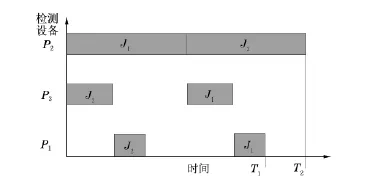
图12 个机组优化后检测流程图

T2=30 min＜80 min，表明优化后的检测设备能满足使用要求，2个机组检测设备数量配置优化前后设备数量与利用率对比见表1。

3.2 当保障3个以上机组（N≥m）的检测流程优化

当N≥m时，这个时候优化问题满足一般性原则，可以利用循环算法求得N个机组检测流程的最优排序，优化的具体步骤如下。

（1）将Pi进行不增排列。在本文中P2＞P3＞P1。

表1 数量与利用率对比

（2）运用循环算法进行最优作业排序。在检测设备P2上依次对J1，J2，J3…Jn进行机务准备作业。在检测设备P3上依次对Jn，J1，J1…Jn-1进行机务准备作业；在检测设备P1上依次对Jn-1，Jn，J1…Jn-2进行机务准备作业。

（3）画出甘特图。根据上面的具体步骤，选取当N=4时举例分析。当N=4时，通过上一小节的计算结果可以知道，当N=4时，把4个机组分成了2批保障，每一批次2个机组，最优检测流程见图2。

T2（4）=30 min＜80 min，表明优化后的检测设备能满足使用要求，2个机组检测设备数量配置优化前后设备数量与利用率对比见表2。

4 小结

分析了保障装备同机组之间的配置关系，以3种武器的装挂前前检测为假设，以保障机组的数量和规定准备时间要求为约束条件，提出外场实弹保障检测设备配置数量的计算方法。利用装备配备的计算公式计算检测设备的配置方案，结合配置方案，对多架飞机保障作业流程进行排序并优化，验证优化后配置方案是否符合要求并同时达到缩短装备检测时间及提高检测设备利用率的目的。最后比较分析了优化前后检测设备的配置个数和利用率，优化后比优化前有了改进，满足了优化的目标。

［1］董肇君.系统工程与运筹学（第二版）［M］，北京：国防工业出版社，2009．

［2］岳奎志，侯志强，等，机群出动能力的Markov模型［J］，系统仿真学报．2008，22（20）：6278-6280.

［3］王绍华，海军机场飞行保障流程仿真及优化［D］，工学硕士学位论文，2012.03.

［4］王禹，刘峰，徐晓东，等，航空装备飞行机务准备时间估算方法研究［J］，数学的实践与认识2012，（4）.

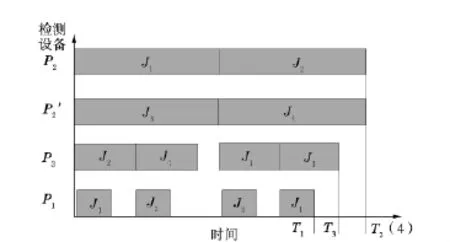
图24 个机组优化后检测流程图

表2 设备数量与利用率对比

〔编辑 利文〕

E926

B

10.16621/j.cnki.issn1001-0599.2016.11.54