电解质溶液热力学模型的研究进展

杜燕萍, 刘 斌, 侯海云, 张东东, 白海浪, 杜丽颖, 李 斌

（西安工程大学 环境与化学工程学院, 陕西 西安 710048）

电解质溶液热力学模型的研究进展

杜燕萍, 刘 斌, 侯海云, 张东东, 白海浪, 杜丽颖, 李 斌

（西安工程大学 环境与化学工程学院, 陕西 西安 710048）

从电解质溶液的经典理论、活度系数模型和近代统计力学理论三个方面，对电解溶液热力学模型的研究进展进行了综述。通过对活度系数模型的分类、组成和发展进行研究，预测电解质溶液热力学模型未来发展方向是从分子和离子角度研究其宏观热力学性质。

电解质溶液；活度系数；热力学模型

在自然界以及各种工业过程，比如化学化工过程中的溶液结晶、环境化工中的废水处理，能源冶金，地球化学，电化学及盐湖工业等过程，电解质溶液可以说是无处不在。对电解质溶液进行理论研究，是这些过程新工艺开发及相平衡研究的理论基础。而电解质溶液的热力学性质，如活度系数，渗透系数，吉布斯自由能等，是化工产品开发及过程设计的重要数据。各国每年都有巨额财政以支持概念设计、工艺过程设计和建设化工厂，而化工过程研究、开发和设计成功的关键就取决于能否从物质微观结构出发，解释、关联和预测电解质溶液的热力学性质。

电解质溶液不同于一般溶液，具有导电性。电解质溶液热力学性质是解决许多工程问题必不可少的工具，在各种化学加工领域中的应用非常广泛。包括：

1、环境应用：如气体处理、污水处理或者化学废物处置；

2、分离过程：如溶液结晶，萃取蒸馏，海水淡化或生物分离；

3、电化学过程：如电解腐蚀和工业生产过程中的不良现象；

4、超临界技术：包括有害剂和超临界流体合成的破坏；

5、能源生产：包括扩大生产井，利用地热能源或抑制天然气水合物的形成；

6、湿法冶金过程。

这些应用，覆盖范围很广的化学组成（如水或混合溶剂，稀或浓溶液）、状态（从常温到超临界状态）和物理现象（如相平衡，酸碱平衡，物质到反应界面的迁移等）。因此，电解质体系理论及模型的发展一直是非常重要的研究课题。

关联和预测水-有机溶剂电解质溶液的热力学性质，需要有系统的实验研究和可靠的理论模型，其中，有些热力学模型已能够表达电解质混合溶剂体系的气液相平衡关系和活度系数。Liddell[1]等认为相平衡体系中存在较强的分子间相互作用力，如果采用液相单一模型模拟关联固–液–汽平衡数据，效果很差。这主要是由于溶液的热力学性质在很宽的温度和浓度组成范围内缺乏可靠的实验数据。因此仅仅从相平衡状态获得模型参数以试图解决热力学可逆问题并不合适。这就需要引进各类实验方法和数据以获得可靠的热力学模型，用于预测热力学性质和平衡状态，从而为化工设计、新型分离过程的开发提供基础数据和模型。

因此，建立电解质溶液热力学模型对研究电解质溶液的热力学性质至关重要，接下来，本文将从电解质溶液的经典理论、活度系数模型和近代统计力学三大方面对近年来电解质溶液体系所应用的理论和模型做一介绍。

1 经典理论

经典电解质理论的基础是离子间存在不同的作用力。可分为：

1.1 非缔合式电解质离子互吸理论

1921年，Lewis等[2]首次提出了电解质溶液的热力学行为。1923年，德拜（Debye）和休克尔（Hü kel）[3]开创了现代电解质溶液理论，他们从离子之间的物理作用出发，提出强电解质离子互吸理论。该理论假设强电解质完全电离，它把离子间复杂相互作用，简化成各个中心离子与周边离子氛的静电引力，故又被称为非缔合式电解质离子互吸理论。

德拜和休克尔提出了离子平均活度系数与离子强度之间的关系式[4]：

式中：z — 离子价数；

I — 离子强度，mol·kg-1。

因为引入一系列假设，导致此式仅适用于很稀的浓度（I ＜ 0.001 mol·kg-1的溶液）。因此又称为Debye-Hükel（简称DH）极限公式。

对于MX型电解质，考虑到中心离子的体积后，当溶液浓度增大，离子氛半径必然减小，在此情况下将中心离子视为点电荷已不合适，若以a表示此位置至中心离子的距离。表达式修正为：

对于非缔合的 1:1电解质，公式可用至 I=1 mol·kg-1的溶液。

半个多世纪以来，很多学者对Debye-Hükel进行改进，扩大它的浓度适用范围。比如Guggenheim[5]在上式基础上，假定Ba = 1并增加了一个线性浓度项bI，浓度范围可到0.1 mol·kg-1左右。

Bromley[6]又通过对 Guggenheim 公式进行修正，得出其计算单电解质离子平均活度系数的计算式：

Bromley公式和DH公式相比较，它可以适用于无离子平均活度系数实验值的体系，这是DH公式不具备的特点；另外，该公式只有一个参数B，但可用于I = 6 mol·kg-1的浓度范围。

虽然在Debye-Hükel模型的基础上，增加参数可以提高模型的浓度适用范围，但这些参数的物理意义尚不明确，不适用于弱电解质和有缔合的电解质溶液体系。

1.2 离子溶剂化（水化）理论

溶剂化是指每一个溶解的分子或离子周围被溶剂分子层牢固包围的现象。水溶液中，溶剂化也叫水化。电解质溶液的非理想性很大程度来自离子在溶液中的溶剂化。对于DH理论和Bromley理论，溶剂分子被看成是不变的连续介质，不仅忽略了离子本身的结构和离子水化作用、溶剂化程度和能力等对离子间相互作用的影响，同时也忽略了离子间静电作用和介质介电常数的关系。在稀释溶液里，这是允许的，但是在高浓溶液里，离子的溶剂化既改变了溶质的浓度，也改变了离子的性质；同样，溶质也影响着溶剂的性质。因此对高浓电解质水溶液而言，溶剂和溶质同样重要。

1948年起，Stokes（斯托克斯）和Robinson（鲁宾逊）[7]考虑到离子和水分子之间存在相互作用力，提出了离子水化理论（SR理论）。即离子是水合的，形成溶剂化离子，当其作用大于离子互吸作用时，活度系数可由随浓度先减小后增大，甚至可大于1。后来，Glueckauf[8]克服了离子水化理论的缺点，引入了过量Gibbs自由能，避免了水的活度的引入，但是同SR理论一样，它也仅限于25 C时的情况。

无论是SR理论还是Glueckauf提出的修正方程均假设离子水化数跟离子浓度无关，两者只适用于稀溶液。因此，Stokes和Robinson后来又提出了离子逐级水化理论[9]，他们假设随着离子浓度的变化，水溶液中离子的水化数随之改变，离子浓度越高，水分子数目越少，离子的水化数也越少。该理论可适用于高浓度的电解质溶液，但较为复杂，目前尚未见其应用于混合电解质溶液。

陆小华[10]提出的以离子水化数为参数的水化模型，可适用于混合电解质溶液的热力学性质计算；并通过分子动力学方法模拟了单个离子的水化现象，提出用“水化因子”的新概念表征离子水化的强弱，并得出离子的鲍林半径大小是决定离子水化强弱的关键因素。应用离子水化理论到强电解质溶液中，水活度的计算结果与实验结果相符合，但对于弱电解质、非电解质和存在缔合的电解质溶液此理论应用较少。

1.3 离子缔合理论

电导、溶剂蒸汽压、拉曼光谱和核磁共振等都证明了即使是强电解质在低介电常数溶剂中也存在离子缔合。离子缔合现象在混合溶剂（如水乙醇混合溶剂）或在高温时会更突出，因此卜耶隆（Bjerrum）[11]提出“缔合理论”。该理论假定：两个带相反电荷的离子彼此接近到某一临界距离因库仑力的吸引而形成离子对，这样的离子对具有一定的稳定性，溶剂分子的碰撞不能拆散它。除了浓度以外，溶剂的介电常数、离子半径等因素也会对离子对的形成产生影响。

根据Bjerrum的理论，q为正负离子互相接近产生缔合时离子间的平均距离，定义为：

式中：z+和z-—正负离子的价态；

e —是单位电荷的电量；

εr—相对介电常数；

kB—Boltzmann常数；

T—热力学温度。

对于25 ºC的水，q = 3.57 |z+z-|。Bjerrum假定，当正、负离子间距小于q时，它们形成“未离解的”的离子对；反之，它们是自由离子。离子缔合理论适用于前者，而德拜–休克尔理论适用于后者。电导实验证明，高价盐在低介电常数溶剂中普遍存在离子对，这与Bjerrum离子缔合理论非常吻合。但是该理论也存在明显的缺点，比如缔合作用力完全是静电作用力，这个理论就不能用[12]。

后来，又出现了一些关于离子缔合的理论，比较突出的是考虑到溶液中的电导性质的 Lee-Wheaton理论[13]和Fuoss理论[14]。

2 活度系数模型

电解质溶液模型的综述文献已有报道。Pitzer[15]等对经验和半经验模型进行了综述。Maurer[16]也对不同时期电解质溶液的热力学研究作出总结。陆小华[17]把电解质在水和混合溶剂体系的热力学模型经典地划分为物理模型、化学模型和化学物理模型。物理模型是典型地基于扩展的Debye–Hückel方程、局部组成理论和统计热力学理论之上。其中有Pitzer模型[18]，Pitzer-Simonson-Clegg模型[19]，eNRTL模型[20]以及eUNIQUAC模型[21]。化学模型是基于离子进行溶剂化反应的假设，其中最重要的热力学模型是Chen模型[22]。以上化学模型都有专门文献对其作详细描述。化学物理模型的代表是陆小华和Maurer[17]提出的混合电解质模型，该模型使用水化平衡的化学作用和UNIQUAC局部组成的物理作用相结合的方法描述电解质溶液的性质。在国内，黄子卿[23]、胡英[24]以及李以圭[25]等曾分别总结过电解质溶液理论方面的研究成果。

统计热力学模型总的说来是既简单又复杂，说其简单是此类模型简化过多，不能真正地表达复杂的电解质溶液；说其复杂是虽然经过简化，结果还是相当复杂冗长，难以求解。因此，与统计热力学模型相比较，工程界更多使用的是从过量吉布斯自由能出发的半经验模型。

混合溶剂–电解质体系的非理想性可通过过量吉布斯自由能（Gex）进行表述，电解质溶液中电解质离子i的活度系数γi可通过Gex求解：

对于活度系数模型（或过量吉布斯自由能模型），每摩尔真实溶液的过量吉布斯自由能通常由三项组成（有的是四项），例如：

式中第一项（lr）代表带电离子间的长程静电作用项，也称作Debye-Hükel（DH）项。通常用非对称的Pitzer-Debye-Hükel（PDH）模型或平均球近似（MSA）理论来表达此项。第二项代表所涉及到的所有物质之间的短程硬球作用项（sr），一般用扩展的非电解质热力学模型，如维里（Virial）方程，Wilson，NRTL，UNIQAC，UNIFAC方程等局部组成模型表达。第三项是所谓的玻恩项或修正的Brünsted-Guggenheim贡献项。玻恩项通常用来解释离子从混合溶剂中的无限稀释态到水相的无限稀释态的离子吉布斯自由迁移能。有些模型还加入了第四项，即中程作用项，用以表达非对称体系参考状态的转换、介电常数与组分及浓度关系的影响。

对于1:1型的电解质MX，玻恩项可表达为：

式中，εs、εw—混合溶剂、水的相对介电常数；

ε0—真空介电常数；

kB—Boltzmann常数；

rM、rX—离子的玻恩半径；

e—单位电荷电量。

另外，有些活度系数模型除考虑长程静电项和短程作用项外，还考虑了化学贡献。比如Lu-Maurer方程[17]提出的适用于单一和混合电解质体系活度系数模型，考虑了离子的单级水化。

无论是哪种过量吉布斯自由能表达式，主要都是由离子长程静电作用项和短程作用项组成。

（1）离子长程静电作用项

Debye-Hükel强电解质离子互吸理论和平均球近似（MSA）理论是基于McMillan-Mayer（MM）渗透压统计理论的原始电解质模型，它们将溶剂看作连续介质，只考虑离子间相互作用。

1973年，Pitzer[26]采用了带电硬球电解质原始模型，从MM理论出发，推导出扩展的Debye-Hükel作为长程静电作用项的表达式，即 Pitzer-Debye-Hükel方程：

以上公式以纯熔盐作为标准态，通过玻恩项可以修正混合溶剂和纯溶剂介电常数的差异。离子长程静电作用项还可通过 MSA理论推导出活度系数的表达式。

（2）短程作用项

短程作用项采用的形式较多，现仅列出主要模型：

① Virial方程

1973年，Pitzer提出的电解质溶液的渗透系数和活度系数的普遍方程，表示如下：

其中，第一项为长程静电作用项，即公式（8）；第二、三项同为表达离子短程硬心效应的维里方程，其中第二项为两粒子短程作用项，包括离子间的色散作用和硬球排斥作用[27]，λij为两粒子作用系数，是离子强度的函数；第三项为三粒子作用项，μijk为三粒子作用系数，略去它与离子强度的关系。

② Margules方程

对于高浓度电解质体系以至纯熔盐体系，质量摩尔浓度很大，Pitzer和李以圭[28]提出的可用于高温、高压、高浓电解质溶液的，Pitzer-Li模型：

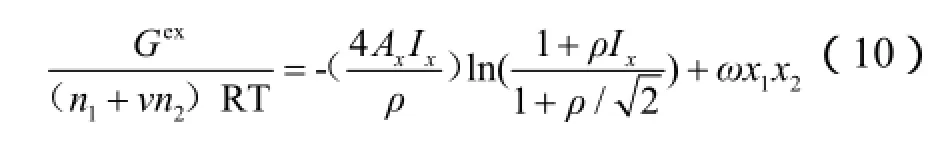
上式等号右边第二项即为短程作用项，是二尾标的Margules方程。

③ eNRTL模型

1968年，Renon和 Prausnitz[29]提出了 NRTL（non-random two liquid）方程，后来，Chen将Pitzer-Debye-Hü kel理论与NRTL方程相结合，提出了Chen-NRTL模型[30]。在此模型中，Chen将过量吉布斯自由能分成两相：即PDH项和由NRTL方程表示的粒子间短程作用项（lc），即局部组成相为：

近年来该模型使用广泛，对于盐效应、汽液平衡和固液平衡方面都有很好的应用。用该模型计算0～6 mol·kg-1浓度范围内电解质水溶液的活度系数精度较高。

④ eUNIQUAC模型

UNIQUAC（universal quasi chemical equations）方程是从似晶格模型和局部组成概念导出的，认为过量吉布斯自由能是由组合项（Gex, C）和剩余项（Gex, R）组成[31]：

Sander[32,33]将反映远程静电作用的 Debye-Hü kel项结合与此方程相结合，提出了扩展的 UNIQUAC方程（eUNIQUAC）。在新的过量吉布斯自由能表达式中，Debye-Hükel（DH）项作为长程静电作用项，短程项用UNIQUAC方程表示，即：

后来，陆小华等[31]分别提出的Lu-Maurer方程，也都包含UNIQUAC方程表示的短程项。

⑤ UNIFAC

UNIFAC（universal functional group activity coefficients）方程是在UNIQUAC方程的基础上提出的，然而它是一种集团贡献法，因此UNIFAC的活度系数计算公式形式上和UNIQUAC相同，但具体处理过程不同。

短程作用项还可分为两类：一类为电解质的原始模型；一类为电解质的非原始模型。前者将溶剂视为连续介质，只考虑离子间相互作用，比如基于Debye-Hü kel理论的模型，MSA理论；后者将溶剂视为作用粒子，在真空介电常数下，同时考虑溶剂分子与离子质点之间的各种相互作用，比如 PS、PSC、eNRTL和eUNIQUAC方程等。长程作用项和短程作用项组合成过量吉布斯自由能表达式的过程中，Pitzer方程的组成形式应用最为广泛。

3 近代统计热力学理论

近年来，随着计算机技术和实验技术的不断提高，人们引入统计热力学，使得电解质溶液理论研究的发展越来越快。从而，很有可能使得电解质溶液理论从原始模型转向非原始模型，并从经典的半经验模型转向分子水平的热力学模型。近年来此方面取得的代表性的工作有：

3.1 积分方程理论（分布函数理论）

积分方程理论从求解溶液中各种粒子的径向分布函数入手，因通常采用Ornstein-Zernike（OZ）积分方程求解，因此称为分布函数理论。该方程在求解过程中未知数过多，为此，常需带入各种假设条件值以获取近似求解，故所求结果很难直接应用。目前，对电解质溶液，应用最为广泛的是“平均球近似理论”（mean spherical approximation，MSA）方法。MSA方程求解简单，已经大量应用于电解质的原始或非原始模型，获得了很好的结果。陆九芳等[34,35]通过对MSA的原始模型进行改进，提出了阳离子有效直径与离子浓度的关系式，并对85种单一电解质和32种混合电解质水溶液中，离子的平均活度系数进行了预测，预测结果比原MSA和Pitzer方程的结果好很多。

3.2 微扰理论

自从1954年Zwanzig[36]创立了流体的微扰理论后，因其能反映溶液的本质及溶剂-溶质间的真实作用，因而发展迅速。微扰理论应用到电解质溶液时，会遇到长程静电积分项无法收敛的问题，因此，要适当考虑参考流体的选择和加速收敛的问题。微扰理论最早的有 Barker-Henderson微扰理论和Chandler-Weeks-anderson微扰理论等，这些理论推导严格，计算复杂；此后又出现了一系列用于实际体系的微扰理论，比如微扰硬链理论（PHCT）和微扰软链理论（PSCT）等；近来，又出现了可用于实际电解质水溶液体系的新微扰理论[25]。胡英等[37]对微扰理论进行了简化，并用此简化的一阶微扰理论预测了气体在电解质水溶液及地下卤水、海水等混合电解质中的亨利系数。

3.3 分子模拟

随着计算机技术的快速发展，计算机分子模拟方法已和理论研究方法并重。它以分子统计力学作为基础，并采用计算机技术，进行分子、离子等微观结构的测定和宏观性质的计算。分子模拟的两种主要方法是蒙特卡洛模拟(Monte Carlo，MC)和分子动力学模拟（molecular dynamics，MD）方法[25]。与非电解质体系相比，目前还不能做到对电解质水溶液通过分子模拟数据直接建立模型流体的状态方程。但是，在极端条件下，比如高温高压以及实验设备极其昂贵时，分子模拟的方法就显得尤为重要。分子模拟的研究对象也将从分子结构简单的体系扩展到结构复杂体系，从单相扩展到多相，从均相扩展到非均相。分子模拟方法也将随着计算机技术的发展，从MC方法逐渐转至MD方法，以实现真正的动力学模拟。Sorensen[38]等分别用MC分子模拟方法计算了KCl在混合溶剂里的活度系数和含盐溶液的汽液相平衡，结果良好。

4 结束语

从理论上，鉴于溶液中各种复杂的相互作用，尤其是在高温高压，混合电解质或混合溶剂体系中，目前还没有哪种活度模型能完全适应各种条件下的电解质溶液体系。因此，很有必要发展新的活度系数模型。从实验上，也可以开展多种研究方法，比如等压法、量热法等，进而可以与电动势法相互补充，相互验证。同时，随着计算机技术的快速发展，可以采用计算机模拟方法，尝试从分子水平上研究复杂的电解质溶液体系的结构和热力学性质，将经典热力学理论与近代统计力学理论、分子模拟方法相结合，以期解决复杂电解质溶液体系。

［1］ K. Liddell. Thermodynamic Models for LiquidLiquid Extraction of Electrolytes[J]. Hydrometallurgy, 2005, 76 (3-4): 181-192.

［2］ G. N. Lewis, M. Randall. The Activity Coefficient of Strong Electrolytes. 1[J]. J. Am. Chem. Soc., 1921, 43 (5): 1112-1154.

［3］ P. Debye, E. Hü ckel. Zur Theorie Der Elektrolyte. I. Gefrierpunktserniedrigung Und Verwandte Erscheinungen. The Theory of Electrolytes. I. Lowering of Freezing Point and Related Phenomena[J]. Physikalische Zeitschrift, 1923, 24: 185-206.

［4］ G. Scatchard. The Physical Chemistry of Electrolytic Solutions[J]. J. Am. Chem. Soc., 1958, 80 (14): 3805-3806.

［5］ R. H. Fowler, E. A. Guggenheim. Statistical Thermodynamics: A Version of Statistical Mechanics for Students of Physics and Chemistry[M]. London: Cambridge University Press, 1939.

［6］ L. A. Bromley. Thermodynamic Properties of Strong Electrolytes in Aqueous Solutions[J]. AIChE J., 1973, 19 (2): 313-320.

［7］ R. R. A. Robinson, R. R. H. Stokes. Electrolyte Solutions (Second Edition)[M]. London: Butterworth, 1965.

［8］ E. Glueckauf. The Influence of Ionic Hydration on Activity Coefficients in Concentrated Electrolyte Solutions[J]. Trans. Faraday Soc., 1955, 51 (0): 1235-1244.

［9］ R. H. Stokes, R. A. Robinson. Solvation Equilibria in Very Concentrated Electrolyte Solutions[J]. J. Solution Chem., 1973, 2 (2-3): 173-191.

［10］ 周健, 陆小华, 王延儒, 时钧. 离子水化的分子动力学模拟[J]. 化工学报, 2000, (02): 143-149.

［11］ N. Bjerrum. Ionic Association. I. Influence of Ionic Association on the Activity of Ions at Moderate Degrees of Association[J]. K. Dan. Vidensk. Selsk, 1926, 7: 1-48.

［12］ 徐滢. 电动势法研究三元体系氟化铷/氟化铯+酰胺+水的热力学性质[D]: 陕西师范大学, 2014.

［13］ W. H. Lee, R. J. Wheaton. Conductance of Symm etrical, Unsym metrical and Mixed Electrolytes. Part 1.-Relaxation Terms[J]. J. Chem. Soc., Faraday Trans. 2: Molecular and Chemical Physics, 1978, 74 (0): 743-766.

［14］ R. M. Fuoss. Conductance-Concentration Function for the Paired Ion Model[J]. J. Phys. Chem., 1978, 82 (22): 2427-2440.

［15］ K. S. Pitzer. Activity Coeficients in Electrolyte Solutions[M]. 1991.

［16］ G. Maurer. Electrolyte Solutions[J]. Fluid Phase Equilib., 1983, 13 (0): 269-296.

［17］ X. Lu, G. Maurer. Model for Describing Activity Coefficients in Mixed Electrolyte Aqueous Solutions[J]. AIChE J., 1993, 39 (9): 1527-1538.

［18］ K. S. Pitzer, G. Mayorga. Thermodynamics of Electrolytes. II. Activity and Osmotic Coefficients for Strong Electrolytes with One or Both Ions Univalent[J]. J. Phys. Chem., 1973, 77 (19): 2300-2308.

［19］ S. L. Clegg, K. S. Pitzer. Thermodynamics of Multicomponent, Miscible, Ionic Solutions: Generalized Equations for Symmetrical Electrolytes[J]. J. Phys. Chem., 1992, 96 (8): 3513-3520.

［20］ B. Mock, L. B. Evans, C.-C. Chen. Thermodynamic Representation of Phase Equilibria of Mixed-Solvent Electrolyte Systems[J]. AIChE J., 1986, 32 (10): 1655-1664.

［21］ I. Kikic, M. Fermeglia, P. Rasmussen. Unifac Prediction of Vapor-Liquid Equilibria in Mixed Solvent-Salt Systems[J]. Chem. Eng. Sci., 1991, 46 (11): 2775-2780.

［22］ C.-C. Chen, P. M. Mathias, H. Orbey. Use of Hydration and Dissociation Chemistries with the Electrolyte-NRTL Model[J]. AIChE J., 1999, 45 (7): 1576-1586.

［23］ 黄子卿. 电解质溶液理论导论（修订版）[M]. 北京: 科学出版社, 1983.

［24］ 胡英. 近代化工热力学—应用研究的新进展[M]. 上海: 上海科学技术出版社, 1994.

［25］ 李以圭, 陆九芳. 电解质溶液理论[M]. 北京: 清华大学出版社, 2005.

［26］ K. S. Pitzer. Thermodynamics of Electrolytes. I. Theoretical Basis and General Equations[J]. J. Phys. Chem., 1973, 77 (2): 268-277.

［27］ 任颖倩. 离子液体调控介质的溶解性能及相关性质的研究[D]. 华东理工大学, 2012.

［28］ 李以圭, K. S. Pitzer. 高温高压下氯化钠水溶液的热力学(I)——在373～573 K及0.1—100 MPa条件下 NaCl-H2O 体系的热力学性质[J]. 化工学报, 1986 (01): 40-50.

［29］ H. Renon, J. M. Prausnitz. Local Compositions in Thermodynamic Excess Functions for Liquid Mixtures[J]. AIChE J., 1968, 14 (1): 135-144.

［30］ C.-C. Chen, H. I. Britt, J. F. Boston, L. B. Evans. Local Composition Model for Excess Gibbs Energy of Electrolyte Systems. Part I: Single Solvent, Single Completely Dissociated Electrolyte Systems[J]. AIChE J., 1982, 28 (4): 588-596.

［31］ X. Lu, L. Zhang, Y. Wang, J. Shi, G. Maurer. Prediction of Activity Coefficients of Electrolytes in Aqueous Solutions at High Temperatures[J]. Ind. Eng. Chem. Res., 1996, 35 (5): 1777-1784.

［32］ B. Sander, A. Fredenslund, P. Rasmussen. Calculation of Vapour-Liquid Equilibria in Mixed Solvent/Salt Systems Using an Extended Uniquac Equation[J]. Chem. Eng. Sci., 1986, 41 (5): 1171-1183.

［33］ 周桓, 李以圭. 电解质溶液相平衡热力学模型研究进展[J]. 计算机与应用化学, 2003 (03): 327-334.

［34］ 于养信, 陆九芳, 李以圭. 平均球近似法计算电解质活度系数的研究(Ⅰ) ——单一电解质水溶液[J]. 化工学报, 1992(05): 523-531.

［35］ 于养信, 陆九芳, 李以圭. 平均球近似法计算电解质活度系数的研究(Ⅱ)——混合电解质水溶液[J]. 化工学报, 1992(05): 532-539.

［36］ R. W. Zwanzig. High-Temperature Equation of State by a Perturbation Method. I. Nonpolar Gases[J]. J Chem Phys, 1954, 22 (8): 1420-1426.

［37］ Y. Hu, D. Lü decke, J. Prausnitz. Molecular Thermodynamics of Fluid Mixtures Containing Molecules Differing in Size and Potential Energy[J]. Fluid Phase Equilib., 1984, 17 (2): 217-241.

［38］ T. S. Sorensen, J. B. Jensen, P. Sloth. Experimental Activity Coefficients in Aqueous Mixed Solutions of KCl and KF at 25 OC Compared to Monte Carlo Simulations and Mean Spherical Approximation Calculations[J]. J. Chem. Soc., Faraday Trans. 1: Physical Chemistry in Condensed Phases, 1989, 85 (9): 2649-2664.

Research Progress in Thermodynamic Models of Electrolyte Solution

DU Yan-ping, LIU Bin, HOU Hai-yun, ZHANG Dong-dong, BAI Hai-lang, DU Li-ying, LI Bin
（College of Environmental and Chemical Engineering, Xi′an Polytechnic University, Shaanxi Xi′an 710048, China）

Research progress in thermodynamic models of electrolytic solution was reviewed from three aspects of the classical theory of electrolyte solution, the activity coefficient model and modern statistical mechanics theory. By studying the classification, composition and development of activity coefficient model, the future development direction of the thermodynamic model of electrolyte solution was predicted.

electrolyte solution; activity coefficient; thermodynamic model

TQ 013

A

1671-0460（2016）11-2632-06

陕西省教育厅专项科研计划项目，项目号：16JK1318；西安工程大学博士启动基金项目，项目号：BS1405；西安工程大学2015年国家级大学生创新创业训练计划项目，项目号：201510709354；国家自然科学基金青年科学基金项目，项目号：21603169。

2016-08-14

杜燕萍（1979-），女，陕西省西安市人，讲师，博士，2013年毕业于陕西师范大学应用化学专业，研究方向：溶液化学。E-m ail：27448084@qq.com。