阻尼振动和受迫振动系统的动力学研究

刘津升

(南京工程学院数理部 江苏 南京 211167)



阻尼振动和受迫振动系统的动力学研究

刘津升

(南京工程学院数理部 江苏 南京 211167)

首先对3种不同情况下的阻尼振动系统进行定量地分析研究，再利用指数方程推导受迫振动的运动方程，分析振子振幅、速度、初相位与驱动力角频率间的关系.分析结果对实际教学和后续科研有一定帮助.

阻尼振动 受迫振动 共振

谐振动是指系统不受外力作用，只在保守内力作用下的物体的周期性往复运动.而现实中，物体的运动总是会受到阻力作用，振幅也会逐渐减小，直至停止.只在回复力和阻力作用下的振动被称为阻尼振动.有时，为了获得稳定的振动，需要对系统施加一周期性的外驱动力，形成受迫振动.振动在生产和科研领域有着重要的应用[1].而教学过程中，许多教材在介绍阻尼振动和受迫振动时，只是直接给出相关结果，并未进行深入地推导和分析.下面利用水平弹簧振子模型对阻尼振动和受迫振动进行定量分析研究.

1 阻尼振动

图1所示为一水平弹簧振动系统，弹簧的劲度系数为κ，振子质量为m,阻力系数为γ.

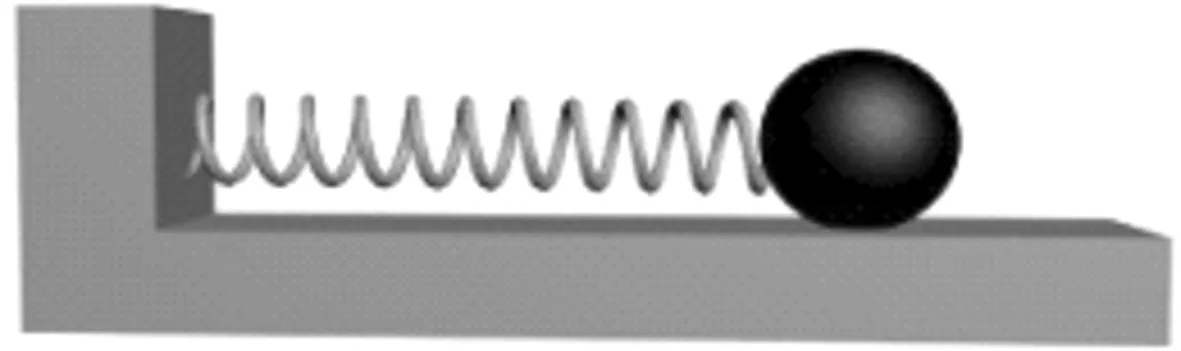
图1 水平弹簧振动系统

假设受到的阻尼力满足f=-γv，则系统的动力学方程可写为

(1)

式(1)为二阶齐次微分方程，其特征方程为

(2)

特征方程根的判别式为

(3)

为了方便计算，令

ω0称为振动系统的固有角频率，δ称为阻尼系数.设振动系统的初始条件满足t=0时，x=A，v=0.很明显对于特征方程式(2)的解有3种情况，下面分别进行展开讨论.

(1)当Δ>0，即δ>ω0时，特征方程式(2)具有两个不相等的实数根，即

微分方程式(1)的解为

(4)

式中，A1和A2为待定系数.代入初始条件有

(5)

图2所示为δ>ω0时，不同阻尼系数下的振动曲线.当δ=0时，振子做周期性谐振动.随着阻尼系数值的增大，振子从初始位置回到平衡位置所需的时间逐渐变长，此时振子做非周期性振动，这种情况称之为过阻尼.

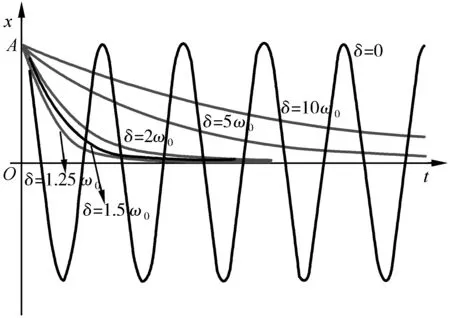
图2 δ>ω0时，不同阻尼系数下的振动曲线

(2)当Δ<0,即δ<ω0时，特征方程的两个共轭复数根为

微分方程的解为

(6)

利用欧拉公式

eiθ=cos θ+isin θ

e-iθ=cos θ-isin θ

式(6)可变换为

x=A1e-δtcos ωt+A2e-δtsin ωt

(7)

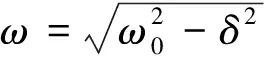
(8)

对式(8)再利用和差化积公式，有

(9)

其阻尼系数δ愈大，振动周期愈长，且振幅减小得愈快.而随着阻尼系数δ的减小，系统也逐渐接近无阻尼条件下谐振动的情况.此时振子做准周期性振动，这种情况称之为欠阻尼.当阻尼系数足够小，即δ=0时，则上式可改写为x=Acos(ωt+φ)，此时又回归到简谐运动形式.

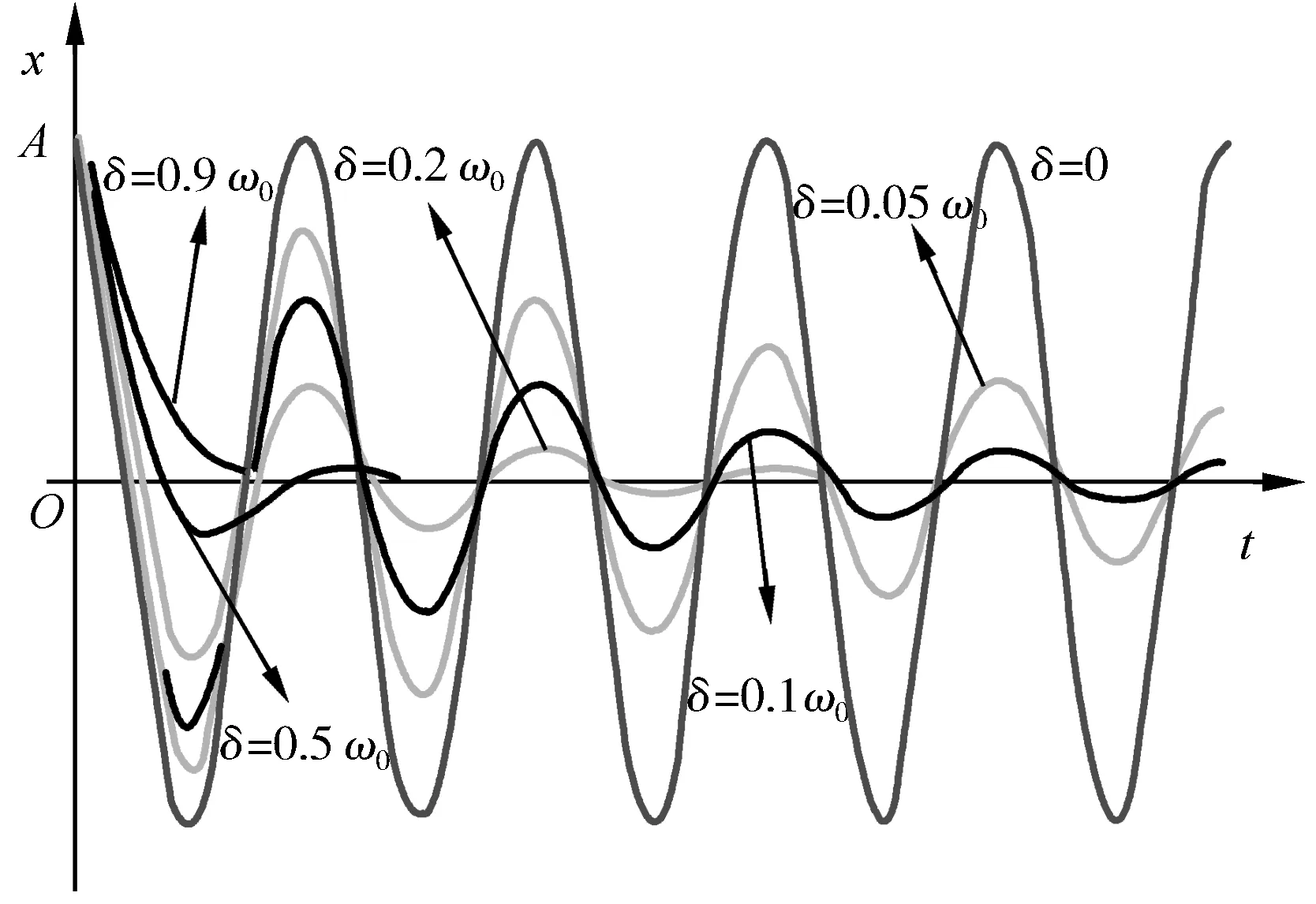
图3 δ<ω0不同阻尼系数下的阻尼振动曲线

(3)当Δ=0,即δ=ω0时，特征方程的两个相等的实数根为

r1=r2=-δ

微分方程的解为

x=(A1+A2t)e-δt

(10)

式中，A1和A2为待定系数.代入初始条件，有

x=A(1+ω0t)e-ω0t

(11)

图4所示为不同阻尼条件下的振动曲线，从图可以看出，当δ=ω0时，振子经过一个较长的时间最终刚好回到平衡位置，这种情况称为临界阻尼.对于无阻尼振动来说，振子做周期性的往复振动.相对于过阻尼状态，临界阻尼状态下振子回到平衡位置的时间最短.欠阻尼状态时，振子做准周期性的运动，其振幅呈指数减小.临界阻尼处于准周期性向非周期性过渡的临界状态.

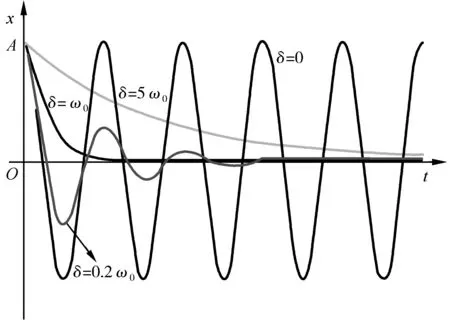
图4 不同阻尼系数下的振动曲线

对于阻尼振动，其任意时刻的机械能可写为

(12)

机械能随时间的变化率为

(13)

由于ma+κx=-γv，所以

(14)

式(14)中右式恒为负数，所以系统的机械能不断减小，且减小量等于阻力对振子所做的功随时间的变化率-γv2=fv，符合能量守恒定律.

2 受迫振动

为了维持稳定的振动，需对阻尼振动系统施加周期性的外驱动力，教材中一般使用余弦函数形式[2,3]，但利用指数形式可以更为方便地解释和说明受迫振动的一些性质.设外在驱动力为F0e-iωdt(实际问题只取其实部)，则振动系统的动力学方程可写为

(15)

式中ωd为驱动力的角频率，根据方程的特征，其解的形式应为x=A′e-iωdt，代入式(15)中，利用欧拉公式，有

(16)

于是式(15)解为

(17)

其中φ′为受迫振动的初相，其值为

我们只讨论式(17)的实部

x=Acos(ωdt+φ′)

(18)

式中，A为受迫振动的振幅，其值为

且是ωd的函数.受迫振动的振幅和初相随驱动力角频率的关系曲线如图5所示.当振幅最大时，满足

此时

随着阻尼系数δ的减小，ωd趋近于弹簧系统的固有角频率ω0，系统初相也趋近于谐振动的初相，其位移振幅也逐渐增大，这种情况称之为位移共振.

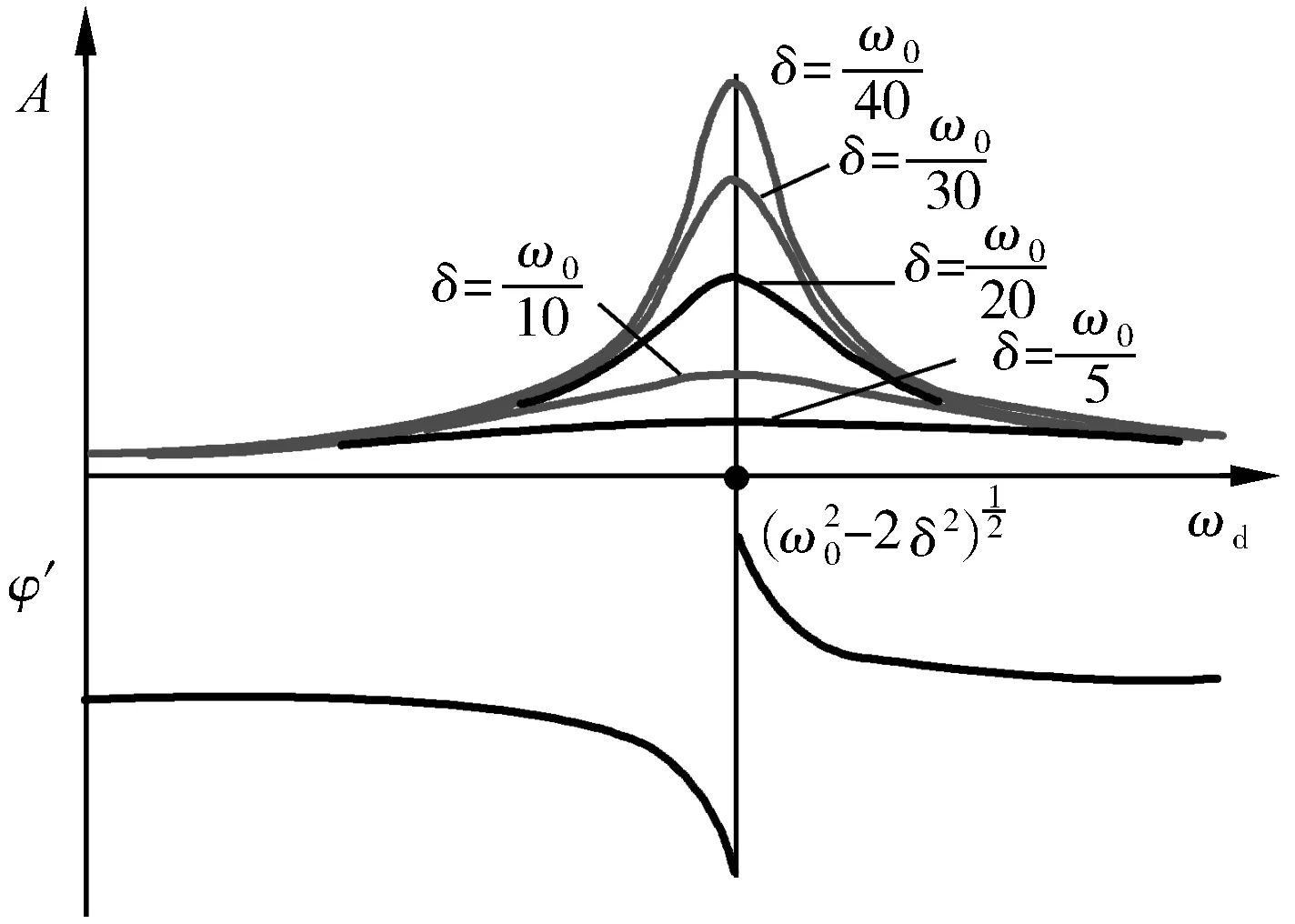
图5 位移共振时的受迫振动的振幅、相位与ωd间的关系

任意时刻，受迫振动系统的振子速度为

(19)

其中，vm为振子的最大速度，其值为

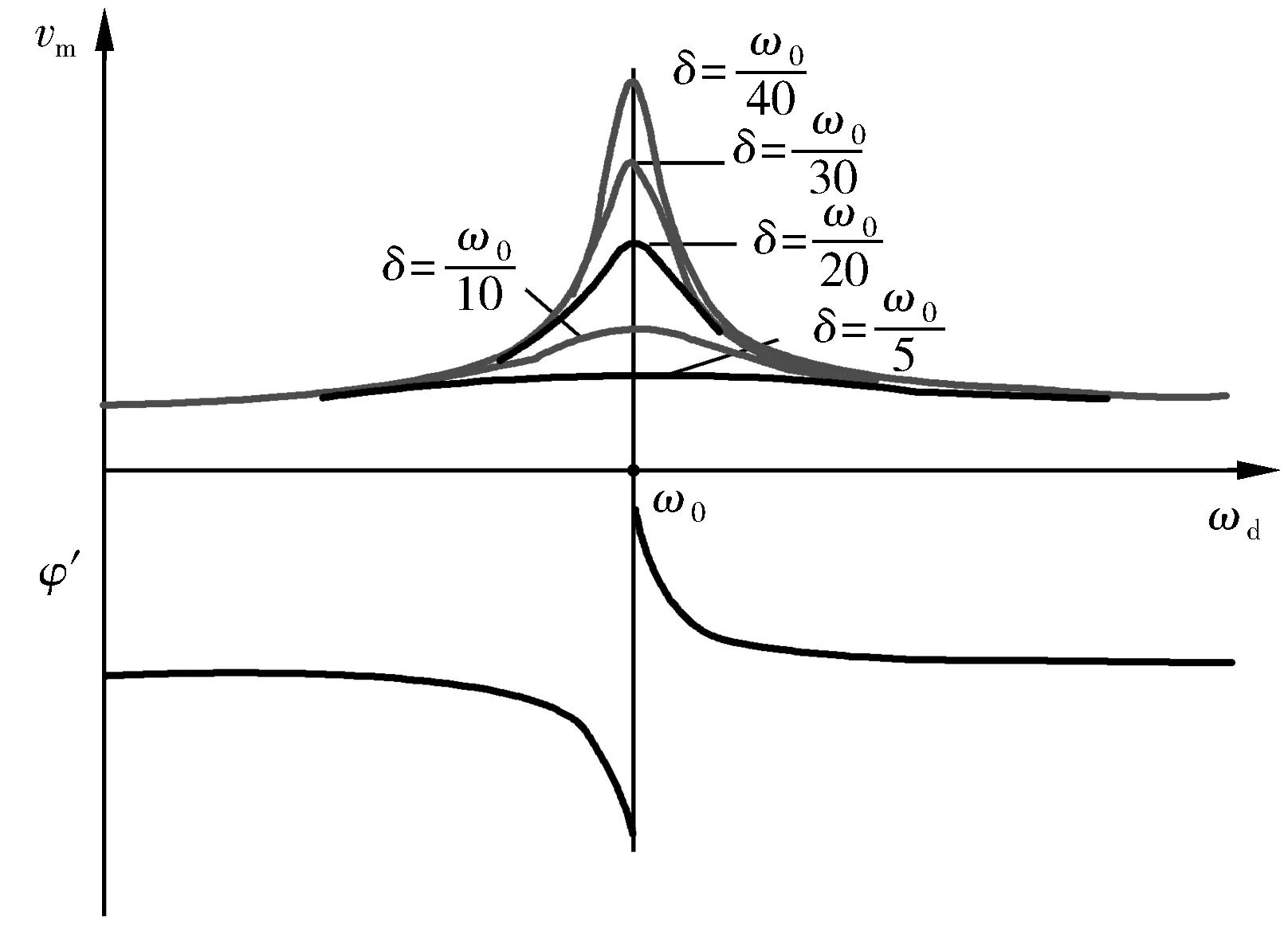
图6 速度共振时的受迫振动的速度、相位与ωd间的关系

通过以上讨论，我们对不同阻尼系数下的振动系统做了定量地分析研究，利用指数方程可以方便地推导和解释受迫振动的相关问题.分析结果对教学和后续科研有一定帮助.

1 Shao Lei, Fang Caihong, Chen Huanjun, et al. Distinct plasmonic manifestation on gold nanorods induced by the spatial perturbation of small gold nanospheres. Nano Letters, 2012, 12(3):1 424～1 430

2 程守洙, 江之永. 普通物理学(下册)(第6版). 北京：高等教育出版社, 2006

3 邓铁如, 孟大敏, 徐元英，等. 西尔斯当代大学物理. 北京：机械工业出版社, 2009

*南京工程学院科研启动基金项目，项目编号：YKJ201538

刘津升(1984- ),男，博士，讲师，主要研究方向为纳米材料.

2016-07-17)