采用基本标识图的Petri网控制策略

马子玥，童 音

(西安电子科技大学 机电工程学院，陕西 西安 710071)



采用基本标识图的Petri网控制策略

马子玥，童 音

(西安电子科技大学 机电工程学院，陕西 西安 710071)

提出了一种基于基本标识图的Petri网的在线监督控制策略．首先根据原Petri网的初始标识与变迁的可控性，建立基本标识图，通过求解整数规划将其中节点标记为合法或弱非法标识．之后基于标记的基本标识图对Petri网中的可控变迁进行在线控制，从而防止系统到达非法标识．该控制策略能够避免可达图的穷举计算，具有良好的效率．

Petri网;监督控制;基本标识

由文献[1]提出的监督控制理论是离散事件系统建模与控制的重要方法．在监督控制理论中，其控制器的设计目标为防止系统进入某些非法状态．早期监督控制理论主要针对自动机模型．在自动机模型中进行控制相对较为简单，可通过迭代算法将由不可控事件指向非法状态的状态标记为弱非法状态，最后在迭代完成之后删除所有的非法状态和弱非法状态就得到了所期望的闭环控制系统．

Petri网是一类广泛使用的离散事件系统模型，具有良好的建模能力．由于Petri网的演化状态是由网结构和标识共同表示，从而避免了状态爆炸问题[2-16]．然而，Petri网中的监督控制问题更为复杂，因为指向非法标识的变迁在其他正常情况下可能仍然在使用，因此不能通过简单的删除变迁来实现控制目的．对于某些特殊问题可以采用信标分析[2-5]、求解许可集合[6-10]、子网特征分析[11]以及笔者之前工作中提出的拓展广义互斥约束控制器[12]来解决，但是对于一般性问题没有很好的解决方案．通常情况下基于区域理论的控制策略[13-14]需要列举Petri网系统的所有可达状态，因此不可避免地遇到状态爆炸问题．

在解决Petri网系统的诊断问题过程中，文献[15-16]中提出了构建基本标识图和压缩一致标识来提升诊断效率的策略．这一策略将系统的可达状态用一组称作基本标识的状态来进行表示．笔者提出了一种基于基本标识图的Petri网在线控制策略，通过构建基本标识图来对系统的状态数进行压缩，在此基础上通过求解线性规划将基本标识划分为许可基本标识与非许可基本标识，从而实现控制目标．

1 基本定义

一个Petri网N可由四元组N=(P， T， Cpre， Cpost)表示，其中P与T分别是m个库所与n个变迁的集合，Cpre与Cpost分别为维度为 m× n、元素为非负整数的矩阵，分别称为N的输入矩阵与输出矩阵．矩阵 C= Cpost- Cpre，是一个以 P× T为序标的整数矩阵，称为关联矩阵．变迁t的输入库所的集合记为·t= {p∈ P| Cpre(p， t)> 0}，输出库所集合记为 t·= {p∈ P| Cpost(p， t)> 0}．

Petri网N=(P， T， Cpre， Cpost)的标识M是一个m维非负整数列向量．N， M0称为初始化的网系统，M0称为N的初始标识．变迁t在标识M下是使能的若 M≥ Cpre(·， t)，记作 M[t．若变迁t在M下使能，t的发射将会使得系统到达新的标识 M′= M+ C(·， t)= M+ Cpost(·， t)- Cpre(·， t)，记作 M[tM′．若从M开始 M[t1M1[t2M2…[tnMn成立，则称标识Mn从标识M可达，记作 M[σMn，σ= t1t2…tn．所有从M可达的标识记为R(N， M)．初始化的网系统N， M0的可达集合记为R(N， M0)．

Petri网中的变迁集合T可以划分为可控变迁集合Tc与不可控变迁集合Tu，其中的元素个数分别记为nc与nu．换言之，一个不可控变迁 tu∈ Tu在M下使能时，tu总是可以发射而不能由外部控制器阻止．

广义互斥约束(Generalized Mutual Exclusion Constraint，GMEC)是一个二元组(w， k)，其中w是m维整数列向量，k为整数．它定义了一组集合 S(w， k)= {M| wT·M≤ k}．拓展的广义互斥约束是一个二元组(W， k)，其中W是 m×r 维整数矩阵，k为r维整数列向量．其定义了一组集合 S(W， k)= {M| WT·M≤ k}．

2 基本标识图

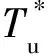
定义2 给定标识M和可控变迁t，其解释向量几何Y(M，t)定义为nc维向量的集合[15]:

Y(M， t)=yσ|σ∈Σ(M， t) ．

定义3 给定标识M和可控变迁t，其最小解释向量集合Ymin(M，t)定义为Y(M， t)中最小元素组成的集合[15]．

最小解释向量的物理含义为: 在标识M1下，若通过发射不可控制变迁到达某个标识M2且可控变迁t在M2下使能，那么所发射的不可控变迁序列σ所对应的发射向量yσ必然不小于Ymin(M1， t)中的任意元素．

假设1 系统中的所有库所与不可控变迁不构成环．

系统中不包括不可控环路这一假设具有现实意义．若现实系统中有不可控制的环路存在，则一旦环路使能，会不可控制地消耗或产出资源(取决于环路增益的正负性)，这样的系统通常是不稳定的．

在满足上述假设的情况下，给定Petri网N、可控/不可控变迁集合Tc/Tu以及标识M，最小解释向量集合Ymin(M， t)可以通过针对关联矩阵变换的操作实现[15]．为简化问题，考虑不可控子网中不包含逆向冲突结构，在该情况下任意Ymin(M， t)只包含惟一元素[15]．

定理1 当满足假设1时，对任意yσ∈Ymin(M1，t)，必然存在至少一个对应的发射序列σ满足 M1[σM2[t．

证明 因为不可控变迁组成的子网是无环的，若存在yσ≥0满足状态方程 M1+ C y≥ 0，则必然存在某个对应的发射序列σ在M下是使能的．

在此基础上通过下述算法生成其基本标识图．

算法1 基本标识图的生成．

输出: 基本标识图B=(V， E)．

步骤1 令V={(M0， 0)}，其中0为标记位．

步骤2 若V中存在标记位为0的元素(M， 0)，则:

步骤3 删除每个顶点的标记位．

结束: 输出B=(V， E)．

定义5 给定Petri网N、可控/不可控变迁集合Tc/Tu，标识M的不可控标识集合定义为

Ru(M)=M′|M[t1t2…tsM′， t1， t2， …， ts∈Tu．

证明 由基本标识图的构造过程可知，y1是M0下t1的最小解释向量．根据定理1，存在相应的发射序列σ1满足 M0[σ1M1．同理，可推知对陈述中的任意Mi都存在相应的发射序列σi满足 Mi[σi+1Mi+1．因此，Ms是可达的，故Ru(Ms)中的标识均可达．

M0[σ1t1M1[σ2t2M2…Ms-1[σstsMs[σs+1M ．

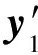
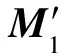
3 在线控制器设计

对于实际物理系统，某些状态是不希望到达的(例如缓存溢出或死锁等状态)．这些状态对应于Petri网模型中的某些标识，被称为非法标识．考虑非法标识由一组拓展的广义互斥约束(W， k)表示，即非法标识集合F定义为 F= {M| WT·M≤ k}．

定义6 若M∈F，则M被称为非法标识．若Ru(M)∩ F ≠ Ø，则M被称为弱非法标识．

根据定义，非法标识同时也是弱非法标识．若系统处于某个弱非法标识，则存在某个由不可控制变迁组成的发射序列使得系统到达非法标识．由于这一发射序列是不可阻止的，因此防止系统进入非法标识集合F控制的目标是防止系统到达某个弱非法标识．

证明 若M是非法标识，则根据定理3，基本标识图B中必然存在路径 M0- (y1， t1)- M1- (y2， t2)- …- (ys， ts)- Ms，M∈ Ru(Ms)．根据定义6，Ms是弱非法标识．

证明 用反证法．假设B中存在路径M0-(y1， t1)-M1-(y2， t2)-…-(ys， ts)-Ms且Ms是非法标识．根据定理2，存在发射序列σ满足 M0[σMs且 σTc= t1t2…ts．因为Ms是弱非法标识，存在非法标识 M∈ Ru(Ms)，因此 Ms[σ′M，σ σ′ 是一个发射序列满足 M0[σ σ′M 且t1t2…ts，与题设矛盾．因此Ms一定不是非法标识．

定理6 一个基本标识M是弱非法标识当且仅当以下整数规划问题存在可行解:

基于以上分析，以下的算法2可实现对系统的在线控制．

算法2 在线控制策略设计．

输出: 在线控制许可集合Cpermit．

步骤1 判断M0是否是弱非法标识．若M0是弱非法标识，则退出．

步骤2 计算基本标识图B=(V， E)，并标记其中的弱非法标识顶点．

步骤3 令当前基本标识Mc=M0．

步骤4 令Cpermit=Tc．

步骤5 对所有可控变迁t∈Tc，检查二元组(Mc， t):

若B中存在M满足Mc-(·， t)-M且M是弱非法标识，则令Cpermit:=Cpermit{t}．

步骤6 输出控制策略Cpermit并等待; //Cpermit集合中的变迁为允许发射的变迁．

步骤7 当观察到某一可控变迁t发生时，更新当前基本标识Mc:=Mc+C y+C(·， t)，其中 Ymin(M， t)= {y}．

步骤8 返回步骤4．

算法2运行时首先通过求解定理6中的整数规划问题判断初始标识M0是否为弱非法标识．若M0为弱非法标识，则不存在可行的控制策略，算法中止．步骤2建立基本标识图并通过求解定理6中的整数规划问题，找出V中的弱非法标识顶点．之后控制器在线依次检查每个可控变迁t发射后的情况．若B中存在M满足 M0- (y1， t1)- M1且M1是弱非法节点，而且允许t1发射，则系统可能到达M1这一弱非法标识，从而进一步到达某一非法状态F．因此，从Cpermit中删除t1，表明在初始状态下通过外部控制器阻止t1发射(无论t1是否使能)．反之，若经t1到达的M1为合法标识，则说明允许t1发射后系统无论如何经过不可控制的变迁序列均不会到达非法标识，故在Cpermit中保留t1．对所有变迁进行检查后系统输出当前的控制策略Cpermit，并停留在步骤6等待．每当控制器监测到某个可控变迁t发射的时候，步骤7对系统当前状态进行更新，之后重新执行步骤4～6，更新当前的控制策略．

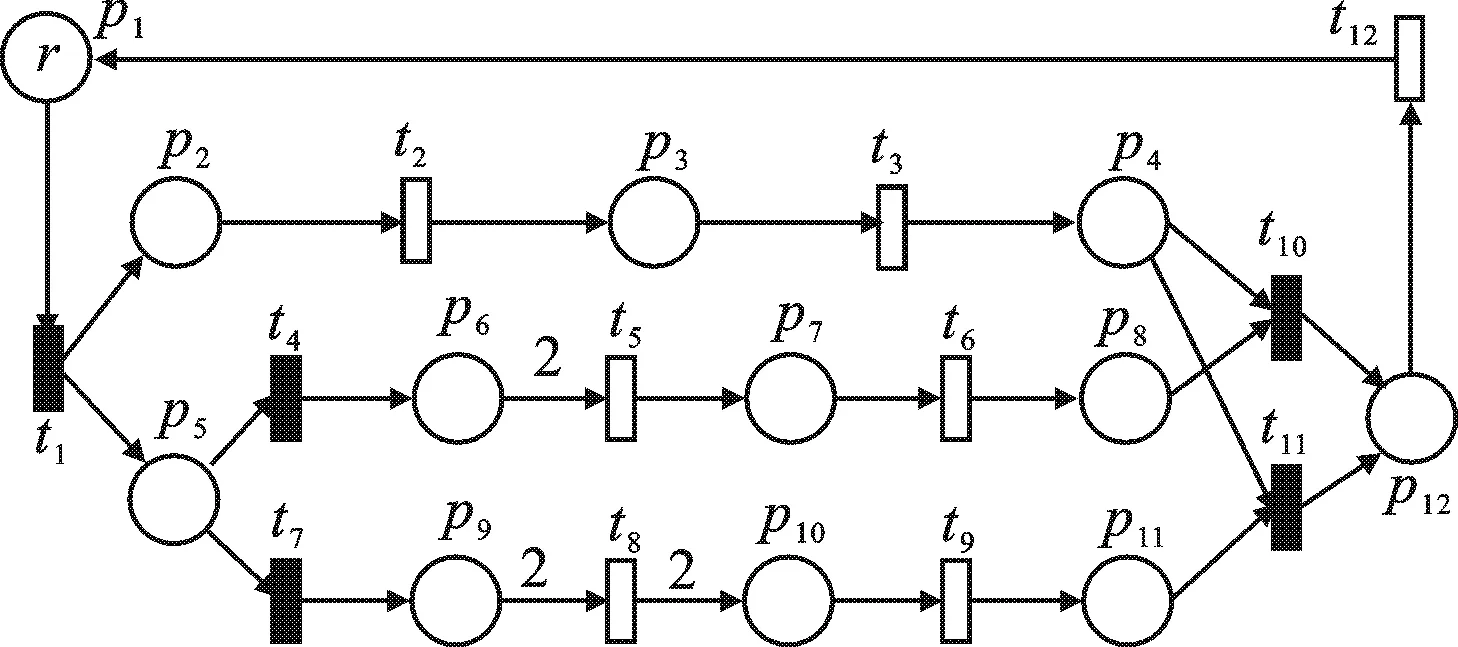
图1 包含3条生产线的自动制造系统

4 算 例

考虑图1中包含3条生产线的自动制造系统．p1代表Idle库所，其中生产线Ⅰ为 p2t3p3t4p4负责生产半成品A．另两条生产线Ⅱ: p5t4p6t5p7t6p8和生产线Ⅲ: p5t7p9t7p10t9p11生成半成品B，并与生产线Ⅰ的半成品A进行组装后得到产品进入库房．系统中可控变迁集合为{t1， t4， t7， t10， t11}，其余为不可控变迁．假设系统的容量为r，即系统的初始标识 M0= rp1．

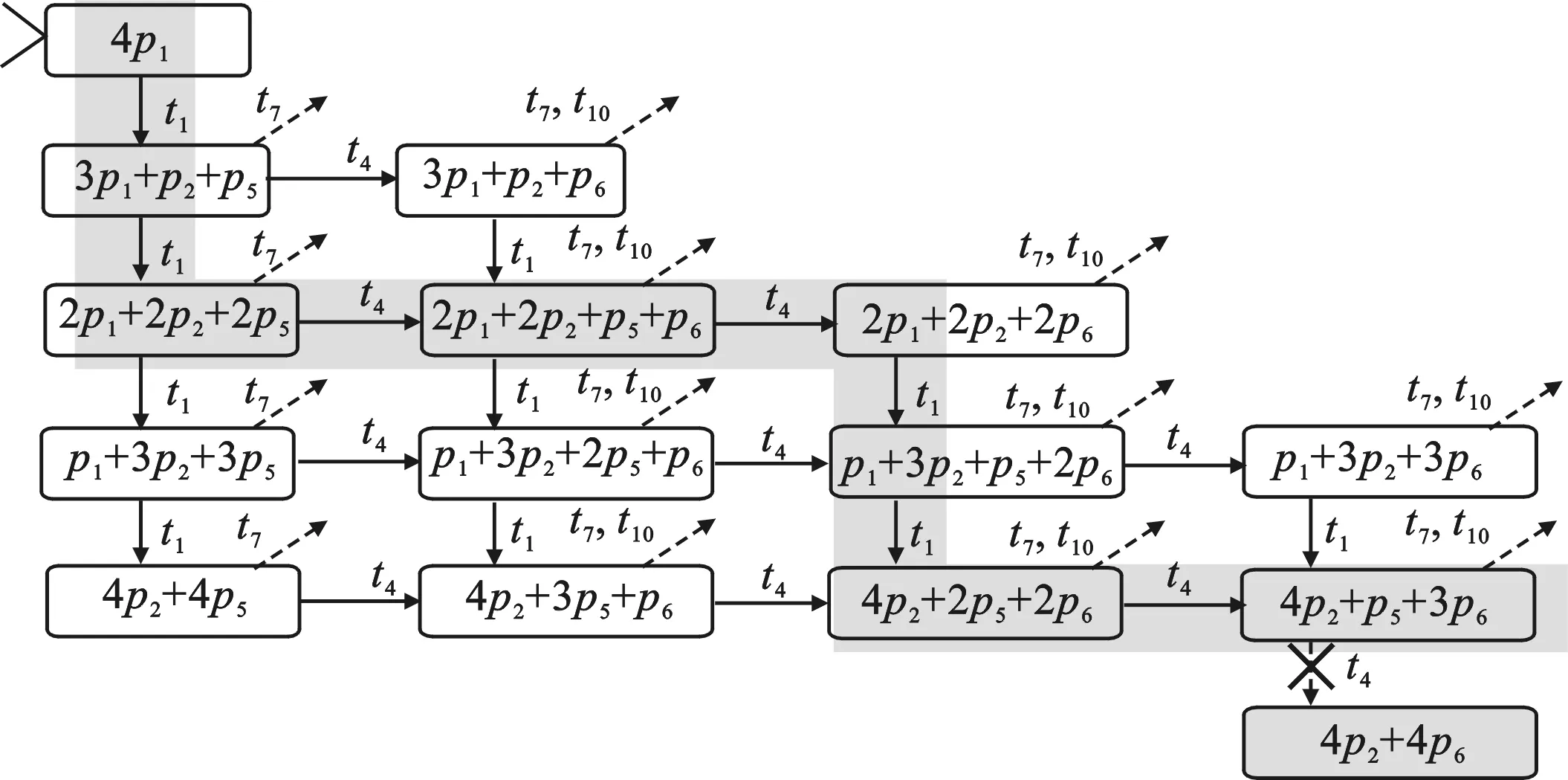
图2 图1中Petri网的基本标识图B(局部)

考虑系统容量r为4的情况，即系统的初始标识M0=4p1．由于系统容量限制，库所p8中的零件数应不超过2，即合法标识M满足 M(p8)≤ 2．因此，非法标识集合F由拓展的广义互斥约束表示为 M(p8)≥ 3．该系统具有 5 423 个可达状态，在此基础上基于区域理论的控制器设计策略需要多次求解包含超过 50 000 个线性约束的整数规划问题．因此，笔者采用上面提出的算法设计在线控制器．算法1构造的基本标识图仅含117个基本标识顶点，通过求解定理6中的整数规划(仅包含12个变量，36个约束条件)判定其中111个为合法基本标识，6个为弱非法基本标识．最终算法1得到一个包含117个状态的在线控制器，其部分列于图2．在初始状态 M0= 4p1下，由于不存在可控变迁指向弱非法基本标识，系统对可控变迁的发射不进行任何限制，即此时的控制策略 Cpermit= {t1， t4， t7， t10， t11}．当系统发射t1后，系统状态迁移至基本标识 M1= 3p1+ p2+ p5，同时输出当前控制策略 Cpermit= {t1， t4， t7， t10， t11}．以此类推，当控制器检测到系统发射了 t1t1t4t4t1t1t4后(灰色路径)到达基本标识 M7= 4p2+ p5+ 3p6，而在该状态下变迁t4指向弱非法基本标识 M8= 4p2+ 4p6．因此，此时控制器的控制策略为阻止t4，即 Cpermit= {t1， t7， t10， t11}，从而防止系统经不可控变迁的发射而到达非法标识．

最后，不同系统容量下的可达图分析控制策略与基本标识图控制器设计策略的对比数据列于表1(测试均采用Matlab工具包)．从表1可以发现，当系统容量增加时，其可达标识数呈指数增长，使得基于可达图的控制器设计策略代价很高．当系统容量 r>8 时，可达图的计算时间已经超过 1 h (可达图包含超过106个可达标识)，意味着基于可达图的区域分析策略已经不可行了．相反可以发现，系统的基本标识数增长缓慢，且远远小于其可达标识数．计算基本标识图的时间仅需计算可达图的1%，其中求解整数规划的计算量占总计算量约5%．因此基于基本标识图的控制策略可以有效地对系统进行控制．

表1 不同系统容量下的可达图RG与基本标识图B的规模

5 结 束 语

针对包含不可控变迁的Petri网系统，笔者提出了一种基于基本标识图的在线控制策略．通过构建基本标识图来对系统的状态数进行压缩，在此基础上通过求解整数规划将基本标识图的顶点划分为合法基本标识和弱非法基本标识，在线控制器与系统并行运行，实时跟踪可控变迁的发射，并阻止系统到达基本标识图中的弱非法基本标识状态．笔者提出的控制算法与传统的基于可达图的控制器设计算法相比，由于避免了可达图的穷举，计算量大大减少，具有较高的效率．

[1] RAMADGE P J G, WONHAM W M. The Control of Discrete Event Systems [J]. Proceedings of IEEE, 1989, 77(1): 81-98.

[2]LI Z W, ZHOU M C. Elementary Siphons of Petri Nets and Their Application to Deadlock Prevention in Flexible Manufacturing Systems[J]. IEEE Transactions on Systems, Man and Cybernetics, Part A: Systems and Humans, 2004, 34(1): 38-51.

[3]LI Z W, ZHOU M C, WU N Q. A Survey and Comparison of Petri Net-based Deadlock Prevention Policies for Flexible Manufacturing Systems [J]. IEEE Transactions on Systems, Man, and Cybernetics, Part C: Applications and Reviews, 2008, 38(2): 173-188.

[4]LI Z W, WU N Q, ZHOU M C. Deadlock Control of Automated Manufacturing Systems Based on Petri Nets—a Literature Review [J]. IEEE Transactions on Systems, Man, and Cybernetics, Part C: Applications and Reviews, 2012, 42(4): 437-462.

[5]张秀艳, 钟春富, 贾建援. S3PR网的可达标识集算法[J]. 西安电子科技大学学报, 2015, 42(5): 105-109.

ZHANG Xiuyan, ZHONG Chunfu, JIA Jianyuan. Method to Compute the Reachability Set of S3PR [J]. Journal of Xidian University, 2015, 42(5): 105-109.

[6]GIUA A, DICESARE F, SILVA M. Generalized Mutual Exclusion Constraints on Nets with Uncontrollable Transitions [C]//Conference Proceedings-IEEE International Conference on Systems, Man and Cybernetics. Piscataway: IEEE, 1992: 974-979.

[7]MOODY J O, ANTSAKLIS P J. Petri Net Supervisors for DES with Uncontrollable and Unobservable Transitions [J]. IEEE Transactions on Automatic Control, 2000, 45(3): 462-476.

[8]BASILE F, CORDONE R, PIRODDI L. A Branch and Bound Approach for the Design of Decentralized Supervisors in Petri Net Models [J]. Automatica, 2015, 52(2): 322-333.

[9]LUO J L, SHAO H, NONAMI K, et al. Maximally Permissive Supervisor Synthesis Based on a New Constraint Transformation Method [J]. Automatica, 2012, 48(6):1097-1101.

[10]MA Z Y, LI Z W, GIUA A. Comments on “Maximally Permissive Supervisor Synthesis Based on a New Constraint Transformation Method” [J]. Automatica, 2015, 51(1): 131-134.

[11]陈晓亮, 蒋忠远, 叶剑虹. 工作流网的混或检测和预防策略 [J]. 西安电子科技大学学报, 2015, 42(2): 77-83.

CHEN Xiaoliang, JIANG Zhongyuan, YE Jianhong. Confusion Detection and Prevention Policies for Workflow Nets [J]. Journal of Xidian University, 2015, 42(2): 77-83.

[12]MA Z Y, LI Z W, GIUA A. Design of Optimal Petri Net Controllers for Disjunctive Generalized Mutual Exclusion Constraints [J]. IEEE Transactions on Automatic Control, 2015, 60(7): 1774-1785.

[13]GHAFFARI A, REZG N, XIE X L. Design of a Live and Maximally Permissive Petri Net Controller Using the Theory of Regions [J]. IEEE Transactions on Robotics and Automation, 2003, 19(1): 137-142.

[14]陈玉峰, 李志武. 安全Petri网事件分离状态的BDD算法 [J]. 西安电子科技大学学报, 2010, 37(1): 119-124.

CHEN Yufeng, LI Zhiwu. Computation of Marking/Transition Separation Instances for Safe Petri Nets Using BDD [J]. Journal of Xidian University, 2010, 37(1): 119-124.

[15]CABASINO M P, GIUA A, SEATZU C. Fault Detection for Discrete Event Systems Using Petri Nets with Unobservable Transitions [J]. Automatica, 2010, 46(9): 1531-1539.

[16]CABASINO M P, HADJICOSTIS C N, SEATZU C. Probabilistic Marking Estimation in Labeled Petri Nets [J]. IEEE Transactions on Automatic Control, 2015, 60(2): 528-533.

(编辑：郭 华)

Supervisor synthesis in Petri nets based on basis marking graphs

MAZiyue，TONGYin

(School of Mechano-electronic Engineering, Xidian Univ., Xi’an 710071, China)

This paper proposes a method to design an online controller based on basis marking graphs for Petri nets. According to the initial marking and the controllability of transitions, a basis marking graph is first computed whose nodes are marked as legal or weakly illegal by solving integer programming problems. Based on the marked basis reachability graph, an online transition disabling rule is computed on-time to prevent the system from reaching illegal markings by firing uncontrollable transitions. This control strategy has a high efficiency since the full enumeration of the reachability graph is avoided.

Petri net; supervisory control; basis marking

2015-11-05

时间：2016-04-01

国家自然科学基金资助项目(61374068, 61472295)

马子玥(1984-)，男，博士，E-mail：maziyue@gmail.com．

http://www.cnki.net/kcms/detail/61.1076.tn.20160401.1622.024.html

10.3969/j.issn.1001-2400.2016.06.012

TP271+8

A

1001-2400(2016)06-0068-06