水驱油田特高含水期含水率预测模型
赵艳武,杜殿发,王冠群,周志海
(中国石油大学(华东),山东 青岛 266580)
水驱油田特高含水期含水率预测模型
赵艳武,杜殿发,王冠群,周志海
(中国石油大学(华东),山东 青岛 266580)
室内实验和矿场实践表明,在水驱油田特高含水期,现有相对渗透率方程不能准确描述油水相对渗透率比值随含水饱和度的变化关系,致使以该方程为前提建立的含水率预测模型在水驱油田开发后期的预测结果产生较大偏差。针对该问题,结合中国大多数水驱开发油田已进入特高含水期的生产实际,提出新型相对渗透率曲线表征方程,利用实际油田的相对渗透率数据,采用最小二乘法进行验证。在此基础上,借助新型相对渗透率表征方程和物质平衡原理,建立适应于特高含水期的含水率预测模型,通过油田实际生产测试资料验证了新模型的实用性和有效性。结果表明,新含水率预测模型的精度高于常用的Logistic模型及Gompertz模型,对特高含水期的含水率动态预测及开发规律认识具有一定的指导意义。
特高含水期;相对渗透率曲线;物质平衡;含水率;预测模型;水驱油田
0 引 言
对于注水开发的油田,含水率预测一直是油田开发工作者不懈研究的课题[1-8]。目前,常见的含水率预测模型包括理论模型与简单数学意义上的增长模型[9],均存在缺点和不足。杨仁峰等人根据Craft等提出的相对渗透率曲线首次推导出含水率理论预测模型,但大量的室内实验观察到,油水相对渗透率比值与含水饱和度在半对数坐标下的高含水饱和度阶段存在“下弯”现象[10],造成直接应用该含水率预测模型预测油田开发动态的效果变差。在前人研究的基础上,首先提出拟合精度高的新型相对渗透率曲线表征方程,在此基础上,推导并建立了适用于特高含水期的新型含水率动态预测理论模型。
1 含水率预测模型的提出
目前,描述油水相对渗透率比值与含水饱和度定量关系较为简洁常用的模型为Craft等提出的公式[11],即:
(1)
式中:Kro、Krw分别为油相和水相相对渗透率;Sw为含水饱和度;a、b为常数。
此外,侯建等人[12]为提高特高含水期油田开采动态预测效果,提出了新型的相对渗透率曲线关系式:
(2)
式中:p为常数。
分析上述2类相对渗透率曲线后发现,实测值与拟合值之间仍有较大差距。为精确定量分析油水渗流特征,提出新的油水相对渗透率比值与含水饱和度的关系表征方程,即:
(3)
式中:c、d为常数。
分别选用贝尔油田、西峰油田与榆树林油田的典型相对渗透率曲线数据,利用式(1)~(3)进行拟合(图1)。

图1 不同形式下的相对渗透率曲线拟合结果
由图1可以看出,3个油田相对渗透率曲线用三次多项式来表征最准确,其几乎与实测曲线完全重合。新型油水相对渗透率比值与含水饱和度关系表征方程在高含水饱和度的下弯段拟合精度较高,故此次研究采用三次多项式来描述相对渗透率关系。基于原含水率预测模型的推导过程及油水相对渗透率比值与含水饱和度关系的新表征方程,推导得到改进的含水率预测模型。在稳定水驱条件下,注水开发油田油井产油量[13]为:
(4)
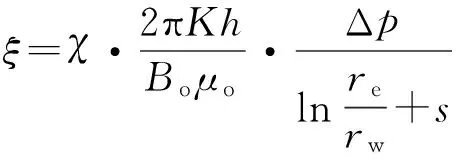
Qo=ξKro(Sw-o)
(5)
式中:Qo为油井产油量,m3/d;χ为单位换算系数;K为地层绝对渗透率,μm2;Kro(Sw-o)为出口端含水饱和度下的油相相对渗透率;h为油层厚度,m;Δp为生产压差,MPa;Bo为地层原油体积系数,m3/m3;μo为地层原油黏度,mPa·s;re为供给半径,m;rw为井眼半径,m;s为表皮系数。
由物质平衡方程可得:
(6)

平均含水饱和度和出口端含水饱和度满足关系式:
(7)

为方便起见,令Sw-o=Sw。联立式(5)~(7),可得:
(8)
对忽略毛管力和重力时的分流量方程分别求一阶、二阶导数,则:
(9)
(10)

将式(9)~(10)带入式(8),可得:
(11)

(12)
式中:Swc为束缚水饱和度;Sor为残余油饱和度;m、n为常数。
将式(12)代入式(11),积分后可得:
(13)

(14)
式中:A、B、C、D为常数,可通过现场含水数据拟合得到。
2 实例分析
东部某油田某区块于1973年投产,1980年底油水井总数为128口,综合含水率为62.08%,年产油113.91×104t/a;1991年底,油水井总数不变,综合含水率为91.15%,年产油为50.70×104t/a,油田开始进入特高含水期。平均水油黏度比为0.1,历史数据清楚,未采取大规模的调整措施,油水井数和生产状况稳定(表1、图2)。
根据相对渗透率曲线,回归得:a=115.14,b=-598.1,c=1 073.4,d=-670.43,m=0.656 13,n=2.482 6,进而有:
(15)
根据含水率随时间动态变化数据(表1)反推得到:A=-1.894 6×107,B=9.561 1×109,C=-1.608 3×1012,D=9.018 5×1013。将拟合结果带入含水率预测公式,可得:
(16)
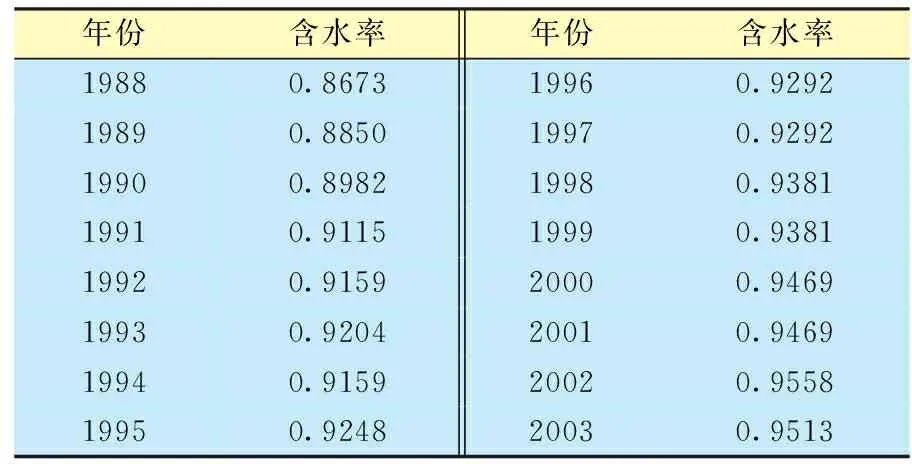
表1 东部某油田某区块含水率数据
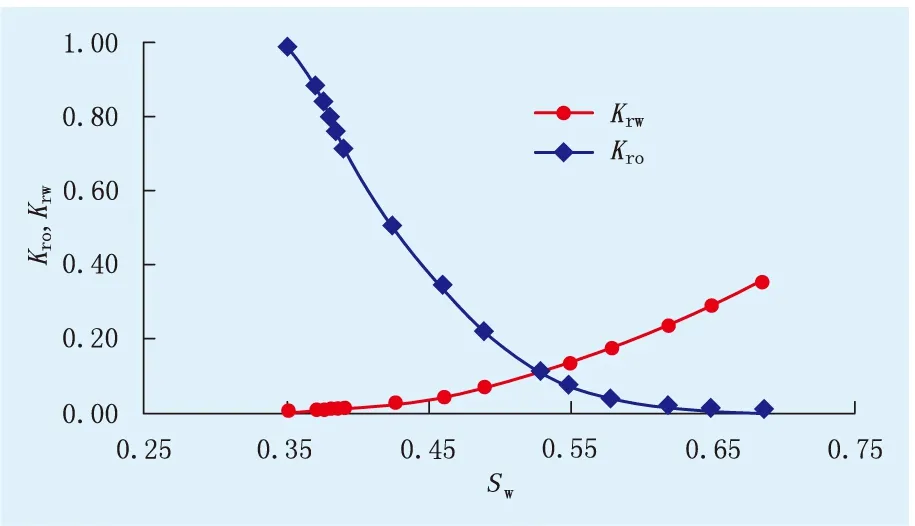
图2 东部某油田油水相对渗透率曲线
根据表2数据,绘制新型含水率模型预测结果与真实情况对比图(图3)。

图3 含水率实际数据与预测值对比结果
为验证新含水率预测模型的精确度,分别利用Gompertz、Logistic和新理论模型对含水率进行预测,并比较预测结果(表2)。其中,Gompertz模型、Logistic模型以及新模型的时间与含水率的相关系数分别为0.965 5、0.960 2、0.993 6,可见新模型较其他2种方法更加准确。
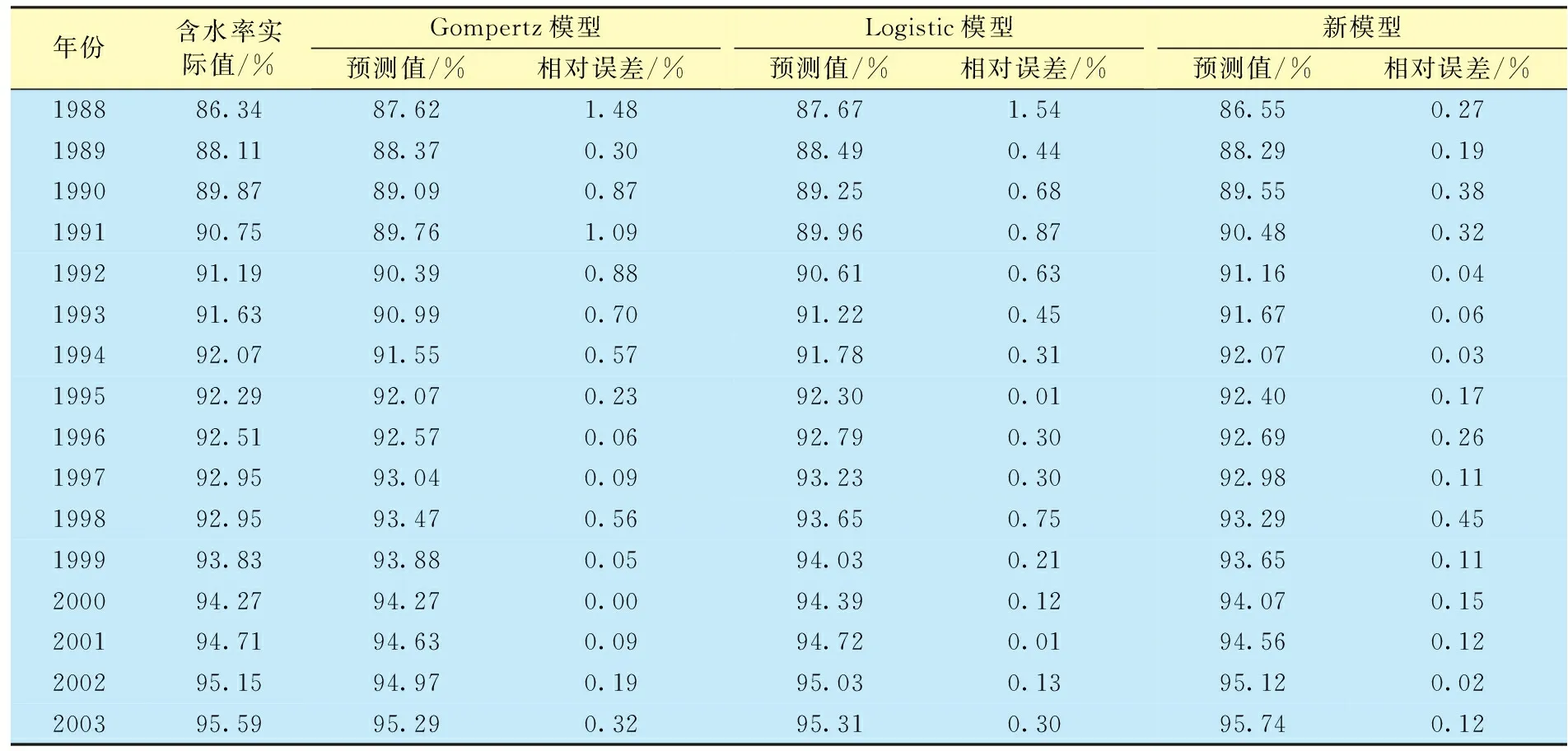
表2 不同含水率预测模型比较
由表2、图3可知,新模型的预测结果与实际情况吻合较好,二者的绝对误差小于1%;与其他2种数学增长模型相比,新建理论预测模型精度较高,当油田综合含水资料丰富时,可利用其建立含水率预测公式,为特高含水期矿场措施实施提供理论支持。
3 结 论
(1) 利用三次多项式表征的相对渗透率公式可准确表征油水相对渗透率随含水饱和度的变化关系。
(2) 借助改进的相对渗透率曲线表征方程推导并建立含水率理论预测模型,利用某油田实际开发数据对该模型进行验证,发现预测的综合含水率随时间变化关系同实际值吻合较好,其相对误差不超过1%。
(3) 结合油田开发现场数据,比较Gompertz模型、Logistic模型和文中预测模型的含水率预测结果,发现新建立模型的预测结果优于其他2种模型,可为矿场实践提供理论支持。
[1] 陈元千.对预测含水率的翁氏模型推导[J].新疆石油地质,1998,19(5):54-56.
[2] 刘鹏程,牟珍宝,刘玉涛.逻辑斯谛旋回模型在预测油田含水率时的修正[J].断块油气田,1999,6(6):40-42.
[3] 田鸿照,彭彩珍,王雪荔.一种预测水驱油田含水率的新模型[J].石油地质与工程,2011,25(1):71-72.
[4] 徐学品,孙健评,孙来喜,等.一种预测水驱油田含水率的模型[J].新疆石油地质,1999,20(2):74-75.
[5] 马春生,万宠文,崔秀敏,等.预测水驱油田含水率的一种新方法[J].大庆石油地质与开发,2006,25(3):43-44.
[6] 杨仁锋,杨莉.水驱油田新型含水率预测模型研究[J].水动力学研究与进展(A辑),2012,27(6):713-719.
[7] 马宏宇,杨青山,杨景强.特高含水期厚油层含水预测方法研究[J].测井技术,2009,33(3):261-265.
[8] 王炜,刘鹏程.预测水驱油田含水率的Gompertz模型[J].新疆石油学院学报,2001,13(4):30-32.
[9] 俞启泰.论Usher、Logistic和Gompertz三种增长曲线的使用价值[J].新疆石油地质,2001,22(2):136-141.
[10] 王小林,于立君,唐玮,等.特高含水期含水率与采出程度关系式[J].特种油气藏,2015,22(5):104-106.
[11] CRAFT B C,HAWKINS M F.Applied petroleum reservoir engineering[M].New Jersy:Prentice Hall,1991:355-365.
[12] 侯健,王容容,夏志增,等.特高含水期甲型水驱特征曲线的改进[J].中国石油大学学报(自然科学版),2013,37(6):72-75.
[13] 姜汉桥,姚军,姜瑞忠.油藏工程原理与方法[M].东营:中国石油大学出版社,2005:78-102.
编辑 姜 岭
10.3969/j.issn.1006-6535.2016.05.027
20151203;改回日期:20160820
中国石油天然气股份有限公司重大专项“塔里木油田勘探开发关键技术”(二期)课题7“碎屑岩油田稳产技术”(2014E-2017)
赵艳武(1990-),男,2015年毕业于中国石油大学(华东)石油工程专业,现为该校油气田开发工程专业在读硕士研究生,主要研究方向为油藏数值模拟及油气渗流理论。
TE341
A
1006-6535(2016)05-0110-04

