基于神经网络的自动机冲击振动信号混沌特征识别

李海广，潘宏侠，任海锋

(1.中北大学 机电工程学院，山西 太原 030051；2.内蒙古自治区白云鄂博矿多金属资源综合利用重点实验室，内蒙古 包头 014010)



基于神经网络的自动机冲击振动信号混沌特征识别

李海广1,2，潘宏侠1，任海锋1

(1.中北大学 机电工程学院，山西 太原 030051；2.内蒙古自治区白云鄂博矿多金属资源综合利用重点实验室，内蒙古 包头 014010)

针对武器自动机含噪冲击振动信号的混沌特性识别问题，提出了基于神经网络的混沌特征识别算法。将信号进行降噪处理，利用神经网络强大的学习和非线性处理能力，逼近信号真实相空间映射建立Jacobian矩阵，通过Jacobian矩阵计算出最大Lyapunov指数，并判断信号是否含有混沌特征。分别采用Lorenz仿真系统和自动机动作的冲击振动实测信号进行算法验证，仿真和试验结果表明提出的算法可以有效地解决自动机冲击振动信号混沌特性识别问题。

自动机；神经网络；混沌； 噪音；冲击振动

自动机是自动武器的核心组成部分，是实现连续发射的各机构的组合，可以完成重新装弹和发射下一发弹的全部动作[1]。在自动机工作过程中，机构相互碰撞会产生冲击振动信号，采集、分析冲击振动信号是诊断、控制自动机的重要途径[2-3]。在冲击碰撞振动问题的研究中，使用非线性动力学混沌理论来分析[4-5]、控制冲击碰撞[6-7]已经得到了学者普遍的认可[8]。其中潘宏侠等[9]对冲击振动数据进行了分析，提出了基于混沌理论的自动机故障诊断技术。由于自动机工作环境复杂，冲击振动信号往往受到不同噪音的影响，所以需要开展混沌特征信号的识别工作。笔者针对自动机含噪冲击振动信号的混沌识别问题，提出基于神经网络[10]的混沌信号特征识别算法。混沌信号的识别主要通过嵌入定理[11]重构相空间并计算最大Lyapunov指数来实现。通常计算Lyapunov指数需要指定相空间的延迟时间和嵌入维数，但对于含噪的混沌特征信号，延迟时间和嵌入维数的选取也受到噪音的影响，进而影响Lyapunov指数正确性。笔者提出基于神经网络的混沌信号识别，主要充分利用神经网络强大的非线性、鲁棒性、自适应性，高精度逼近含噪信号相空间的真实映射，准确有效地计算冲击振动信号最大Lyapunov指数，进而开展混沌识别。开展了仿真试验和自动机射击试验，数据结果表明该算法可以有效地解决自动机冲击振动信号混沌特性识别问题。

1 神经网络混沌特征识别算法

笔者提出的基于神经网络混沌特征识别算法如图 1所示，算法的核心为混沌信号识别：降噪后的信号，通过神经网络逼近其相空间真实映射F后，计算Jacobian矩阵、最大Lyapunov指数，如果Lyapunov指数为正，信号存在混沌；指数为负，则不存在混沌。

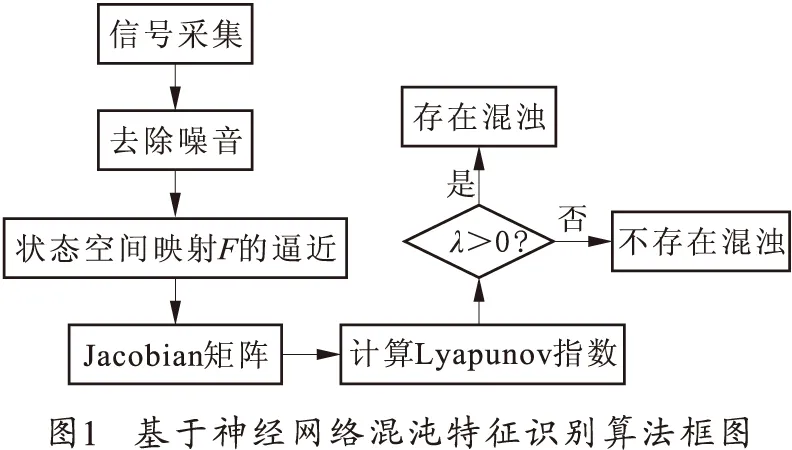
1.1 噪音去除

混沌信号降噪的方法很多，如构造代替函数法、局部平均法、局部投影法、小波分解等。不同的降噪方法，存在不同的局限性[12]，如构造代替函数法需要预先了解混沌系统动态特性；局部平均法中简单的局部线性近似，并不能充分刻画混沌信号的非线性动力学特性；局部投影法受限于合适的投影领域选择问题。小波的降噪方法虽然存在小波基及分解层数的选择问题，缺乏较好的自适应性，但凭借着时频域内很强的信号局部分析能力，以及多分辩分析的特点，对于含噪混沌信号能够取得良好的降噪效果[13]。在笔者所提出的混沌识别算法中，降噪环节采用小波分解降噪方法，采用离散Meyer小波基对信号进行10尺度小波分解，由于分解信号具备不同的频率特性范围，其中高频噪音信号主要集中在高频小波分量上，基线漂移噪音主要为缓变趋势分量，在重构过程中将高频分量、缓变趋势分量去除，进而实现噪音的消除。

1.2 基于神经网络的映射F逼近

xt=f(xt-L,xt-2L,…,xt-mL)+εt

(1)

式中:εt为噪音成份;L为时延;m为嵌入维数，其相空间表达式为

(2)

采用前馈神经网络逼近真实相空间未知映射F，前馈网络包括输入层、隐含层和输出层，学习模式采用BP算法，如图 2所示。

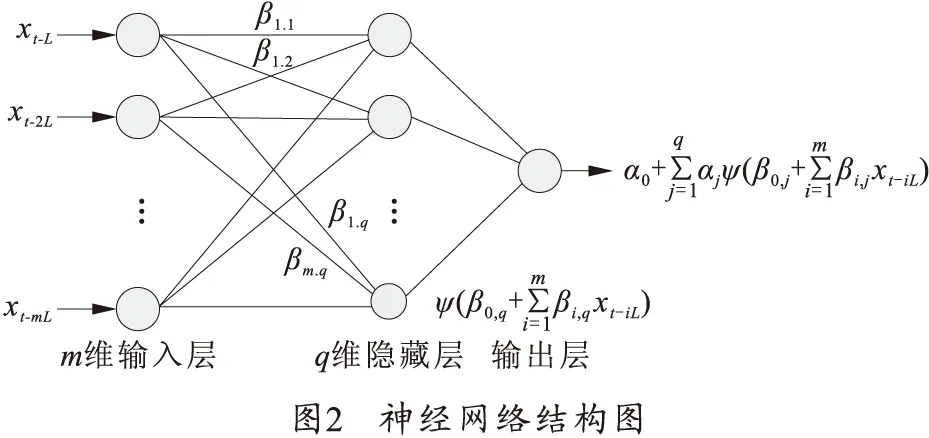
使用式(1)中的(xt-L,xt-2L,…,xt-mL)作为一个m维的输入层，整个信号被传递到一个q维隐藏层，连接权值为βi,j，其中i=1,2，…,m；j=1,2，…,q，隐藏层第j个神经元将接收输入层所有输入元的信号加权之和，此外每个神经元还有本身的初始阀值β0,j，神经元的传递函数采用Sigmoid函数，整个q维隐藏层与输出层连接权值为αj,初始阀值为α0，原始信号真实混沌映射F可以由式(3)进行逼近。

(3)

1.3 信号最大Lyapunov指数的计算

由混沌理论可知，在测量信号所构建的相空间内，最大Lyapunov指数反映了相空间内系统相邻轨道收敛和发散的长期平均水平。如果相空间存在混沌，最大Lyapunov指数为正，不存在混沌则为负。

因为时间序列测量信号的初始条件已经确定，因此不能直接计算Lyapunov指数，Wolf等[14]提出定义符合观测数据的微分预测模型，通过预测模型计算Lyapunov指数，但这种方法受限于系统测量误差、噪音的影响。另一种方法是由Eckmann等[15]提出的Jacobian矩阵计算方法，虽然测量信号的动力系统未知，不能重构信号相空间的真实映射F，但是可以通过重构嵌入空间进而得到与原始未知动力系统相同的不变量特性。

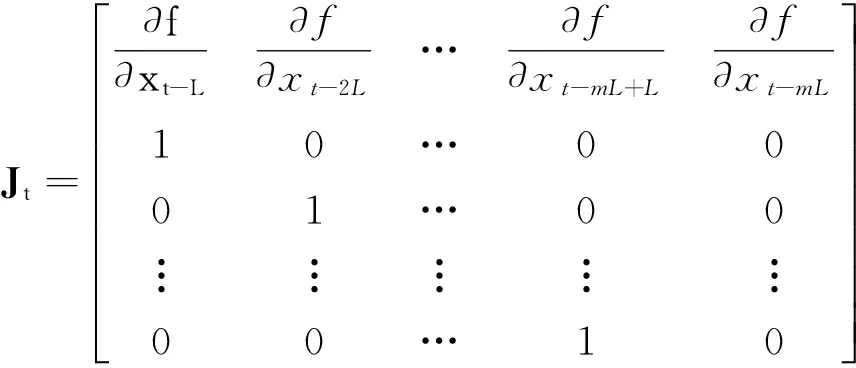
(4)式(4)为Jacobian矩阵，通过逼近真实相空间映射F计算出Jacobian矩阵，进而在相空间内线性逼近真实运动轨迹，两轨迹的对数分离程度Lyapunov指数测量经过M步时延后计算公式为

(5)

2 算法仿真

在仿真算法中使用无量纲Lorenz方程，如式(6)所示。

(6)

式中，选取参数a=16，b=4，c=45.92,采用四阶龙格-库塔积分算法，积分初始值为(1,0,1)，积分步长为0.01。选取Lorenz系统中x分量并附加上高斯噪音，如式(7)所示。

x=x+randn(0,1)×Slevel×std(x)

(7)

式中:x表示含噪信号;std(x)表示x的标准差; randn(0,1)表示产生正态分布的随机数;Slevel为噪音强度，分别选择0、0.05、0.5、1、2，计算含噪音的x分量，如图 3所示。

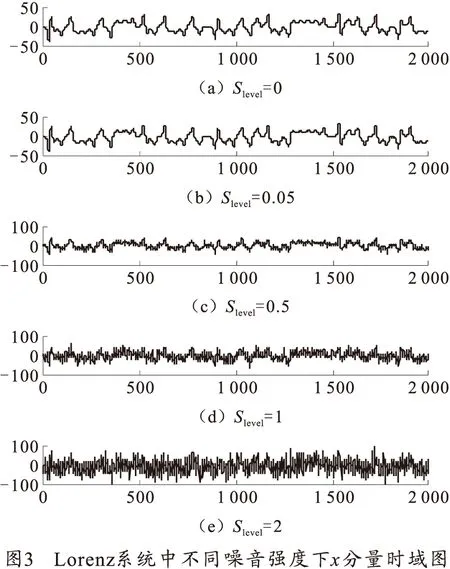
使用神经网络逼近相空间真实映射的最大Lyapunov指数计算方法，计算图3中各含噪x分量的最大Lyapunov指数，如图4所示，通过观察可以发现，最大Lyapunov指数随着噪音强度增加而降低，噪音对于混沌的识别有显著的影响，随着噪音强度的增加，信号的混沌特性逐渐湮灭在噪音信号之中。

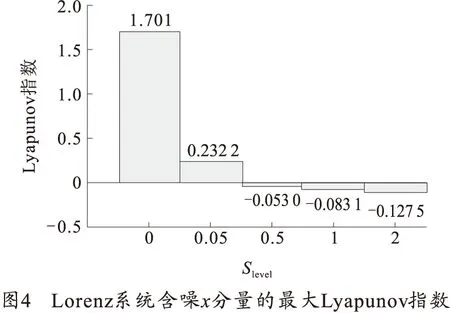
图5为使用笔者所提出的算法计算出图 3各含噪x分量的最大Lyapunov指数，并与图 4对比可知，提出算法计算得到最大Lyapunov指数均指示出Lorenz系统各含噪x分量具有混沌特征。

3 自动机冲击振动试验

3.1 试验台及其测点布置

试验研究的对象为国产某型高射机枪，采用导气式自动机，其工作原理为：子弹发射后，部分火药燃气进入导气室，推动运动活塞，完成机枪开锁、抛壳、供弹等自动循环动作。由于自动机的构成比较复杂，各个机构之间多是以曲面或者棱角的形式相接触，因此布置测点来安放传感器比较困难，经过对比自动机各机构的位置和考虑传感器安放的可行性，最终选择了在机枪尾部上方和机匣的前侧上方来布置测点，具体测点位置如图6所示。加速度传感器采用PCB公司型号350A14量程为10 000g的单向加速度传感器，以枪口正前方为x轴正方向，枪口左方向为y轴正方向建立坐标系。本试验在机枪射击靶场进行，用比利时LMS系统进行信号的采集工作，设置采样频率为204.8 kHz。

3.2 冲击振动信号的截取

高速自动机在其运动循环过程中会完成闭锁、激发、开锁等过程，每一个动作过程伴随着一个或几个冲击振动过程。在连续射击过程，每一发子弹的射击过程是相同的，整个过程呈现出以每发子弹射击时间为周期的冲击振动信号。 图7为截取的5连发射击冲击振动信号，每发子弹的冲击振动信号可以根据动作过程截取出每个动作的冲击振动信号，如图8所示。图8(a)为5连发中第4发子弹射击过程、图8(b)为其闭锁过程。

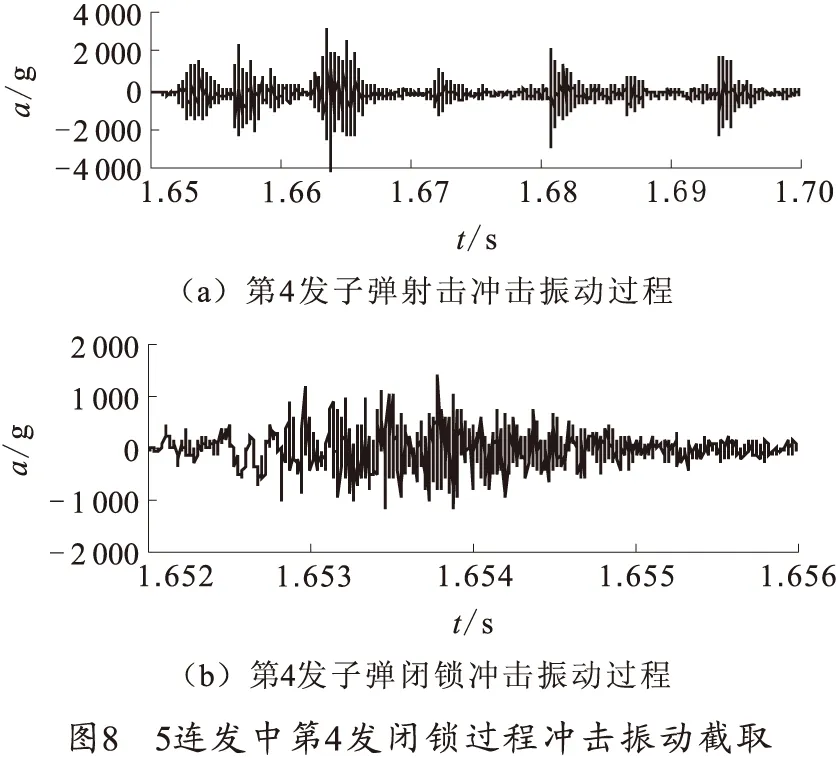
在试验设计工况下，实弹射击依次按照单发、3连发、5连发顺序进行射击，其中单发射击，射击3次，共3发子弹；3连发射击2次，共6发子弹；5连发射击1次，共5发子弹，总计射击14发子弹。

4 实测信号分析

4.1 未降噪信号分析

在不进行对实测信号降噪处理的条件下，使用神经网络逼近相空间真实映射的最大Lyapunov指数计算方法，计算出图8(b)闭锁冲击振动信号的最大Lyapunov指数为-0.101 2，根据混沌的Lyapunov指数判定方法可以分析出，图8(b)冲击振动信号并不是混沌信号，噪音信号掩盖了混沌成分。采用同样的方法将试验中14发子弹发射过程中所有闭锁冲击信号进行最大Lyapunov指数的计算，结果如图9所示，所有的冲击振动信号均受到噪音的干扰，均没有显示出具有混沌特性。

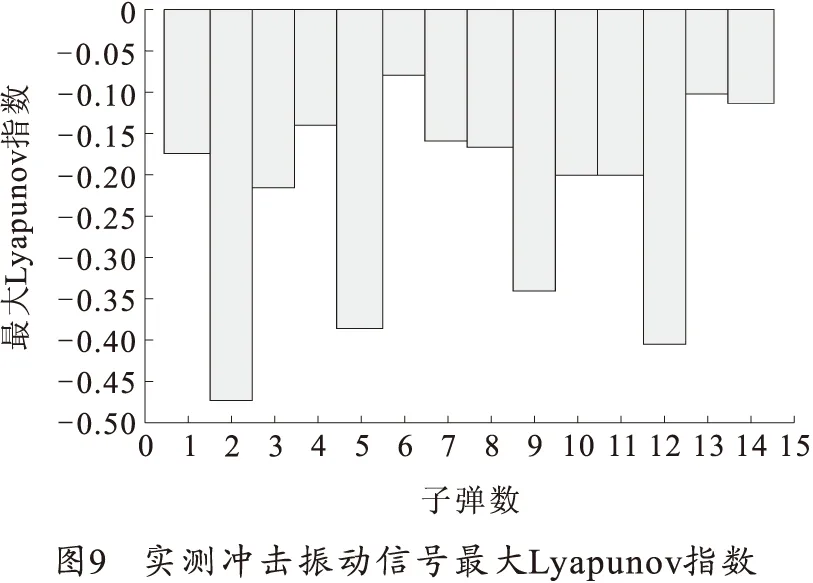
4.2 降噪信号分析

对于图8(b)冲击振动信号，采用离散Meyer小波进行10尺度分解降噪后，结果如图10所示。使用神经网络的最大Lyapunov指数算法，计算最大Lyapunov指数，结果为0.357 1，表明小波降噪有效地去除了原信号中的噪音成份，最大Lyapunov指数表征出该冲击振动信号具有混沌特性。

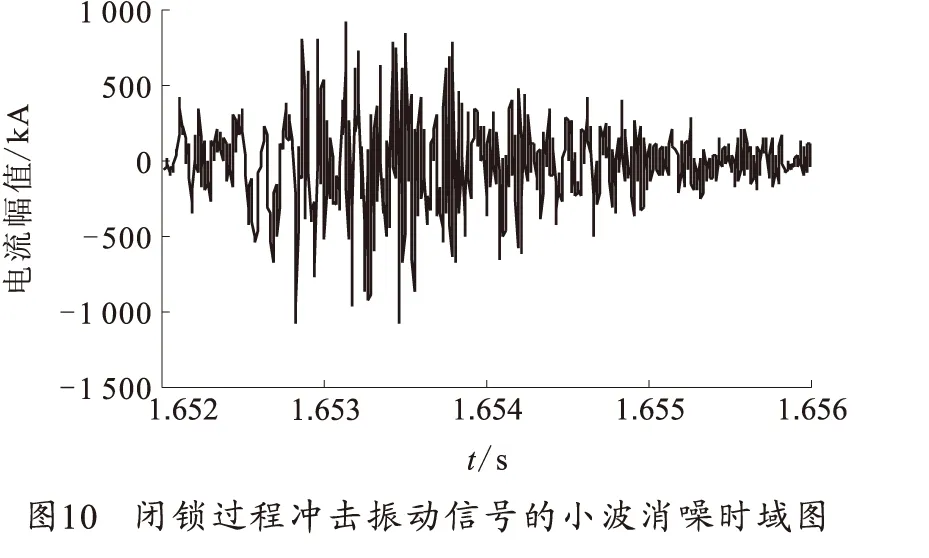
使用相同的小波降噪方法，将试验中的14发子弹所有闭锁冲击信号进行降噪处理，并计算最大Lyapunov指数，结果如图 11所示，根据最大Lyapunov指数数值大小，可以将14发子弹中混沌特性显著的信号识别出来，如第4、8～14发的闭锁冲击振动信号具有显著的混沌特性。与图9对比可以发现，小波降噪后所有冲击闭锁过程的最大Lyapunov指数均有所提高，但并不是所有的冲击信号降噪后显示出明显的混沌特性，这是因为自动机动作环境的复杂性，不同的冲击振动信号能量不同，造成冲击振动信号的混沌特性不同。

5 结论

笔者提出基于神经网络的最大Lyapunov指数算法，处理自动机冲击振动信号中混沌成分的识别问题，仿真Lorenz系统和某高射机枪试验数据处理表明，该方法可以准确地判断信号的混沌特性，可以有效解决自动机冲击振动信号混沌特性识别问题。

References)

[1]薄玉成，王惠源. 自动机结构设计[M].北京：兵器工业出版社, 2009 ：1-2. BO Yucheng,WANG Huiyuan. Automatic machine structure design[M]. Beijing:The Publishing House of Ordnance Industry,2009: 1-2.(in Chinese)

[2]潘宏侠，马百雪，许昕. 基于小波尺度谱重排与小波排列熵的自动机故障诊断[J]. 火炮发射与控制学报, 2015，36(2): 64-67. PAN Hongxia,MA Baixue,XU Xin.Fault diagnosis of automatic cannon based on wavelet scalogram rearrangement and permutation entropy[J].Journal of Gun Launch & Control,2015,36(2):64-67.(in Chinese)

[3]潘铭志，潘宏侠，赵润鹏，等.自动机机箱振动分析与诊断研究[J].火炮发射与控制学报,2012 (2):67-70. PAN Mingzhi,PAN Hongxia,ZHAO Runpeng,et al.Automatic receiver vibration analysis and diagnosis research[J].Journal of Gun Launch & Control,2012(2):67-70. (in Chinese)

[4]FENG Jinqian, LIU Junli.Chaotic dynamics of the vibro-impact system under bounded noise perturbation[J].Chaos, Solitons & Fractals, 2015, 73: 10-16.

[5]魏艳辉，徐洁琼，黄龙生. 两自由度碰撞振动系统的Lyapunov指数谱分析[J]. 振动与冲击, 2009,28(1): 60-63，195. WEI Yanhui， XU Jieqiong，HUANG Longsheng. Spectral analysis of Lyapunov exponents for a two-degree-of-freedom vibro-impact system[J]. Journal of Vibration and Shock, 2009, 28(1): 60-63，195. (in Chinese)

[6]苟向锋，罗冠炜，吕小红. 含双侧刚性约束碰撞振动系统的混沌控制[J]. 机械科学与技术, 2011, 30(8): 1262-1266. GOU Xiangfeng,LUO Guanwei,LYU Xiaohong. Chaos control of a two-degree-of-freedom vibrating system with two rigid constraints[J]. Mechanical Science and Technology for Aerospace Engineering,2011,30 (8): 1262-1266. (in Chinese)

[7]KOU C W, SUH C S. Controlling bifurcation and dynamic behavior in vibro-Impact System[C]∥ ASME 2014 International Mechanical Engineering Congress and Exposition. Montreal Canada：American Society of Mechanical Engineers.Montreal,Canada:IEEE,2014:1-8.

[8]丁旺才，谢建华. 碰撞振动系统分岔与混沌的研究进展[J]. 力学进展, 2005, 35(4): 513-524. DING Wangcai, XIE Jianhua. Advances of research on bifurcations and chaos in vibro-impact system[J].Advances in Mechanics, 2005, 35 (4): 513-524. (in Chinese)

[9]潘宏侠，崔云鹏，王海瑞. 基于混沌理论的自动机故障诊断研究[J]. 火炮发射与控制学报,2014,35(2):50- 54.

PAN Hongxia,CUI Yunpeng,WANG Hairui.Study on automaton fault diagnosis based on chaos theory[J].Journal of Gun Launch & Control, 2014,35(2):50-54. (in Chinese)

[10]BENSAIDA A, LITIMI H. High level chaos in the exchange and index markets[J]. Chaos, Solitons & Fractals, 2013, 54: 90-95.

[11]TAKENS F. On the numerical determination of the dimension of an attractor[M].Berlin:Springer Berlin Heidelberg, 1985:99- 106.

[12]王小飞,曲建岭,高峰,等.基于噪声辅助非均匀采样复数据经验模态分解的混沌信号降噪[J]. 物理学报, 2014, 63(17): 18-26. WANG Xiaofei,QU Jianling,GAO Feng,et al. A chaotic signal denoising method developed on the basis of noise-assisted nonuniformly sampled bivariate empirical mode decomposition[J]. Acta Physical Sinica, 2014,63(17):18-26. (in Chinese)

[13]刘云侠,杨国诗,贾群. 基于双提升小波的自适应混沌信号降噪[J]. 电子学报, 2011, 39(1): 13-17. LIU Yunxia, YANG Guoshi, JIA Qun. Adaptive noise reduction for chaotic signals based on dual-lifting wavelet transform[J]. Chinese Journal of Electronics, 2011, 39(1): 13-17. (in Chinese)

[14]WOLF A，SWIFT J B，SWINNEY H L，et al. Determining Lyapunov exponents from a time series[J]. Physica D: Nonlinear Phenomena, 1985, 16(3): 285-317.

[15]ECKMANN J P，KAMPHORST S O，RUELLE D，et al. Lyapunov exponents from time series[J]. Physical Review A, 1986, 34(6): 4971-4979.

Chaotic Characteristics Identification of Automatic Gun Impact Vibration Signal Based on Neural Network

LI Haiguang1,2, PAN Hongxia1, REN Haifeng1

(1.College of Mechatronic Engineering，North University of China, Taiyuan 030051, Shanxi, China；2. Inner Mongolia Key Laboratory for Utilization of Bayan Obo Multi-metallic Resources,Baotou 014010, Inner Mongolia, China)

In response to the issue of identifying the chaotic characteristics of automatic gun impact vibration signals, this paper puts forward an identification caculation method based on the BP neural network. Firstly, a method is used to reduce the noise in the signal measured. Secondly, based on the robust nonlinear reflection and training function of artificial neural networks, the optimal direction estimation of the signal real map can be obtained to create the Jacobian matrix from the output of the neural network, for the method of the Jacobian based approach can estimate the maximum Lyapunov exponent and judge if the signal has chaos. Positive maximum Lyapunov exponent was obtained from the signals, showing certain chaos features. Both the chaotic Lorenz simulation signal and the automatic gun impact vibration signal are respectively used for identitying the chaos property with the proposed method. Simulations and experiments verified the validity of the proposed method.

automatic gun; neural network; chaos; noise; impact vibration

10.19323/j.issn.1673-6524.2016.04.018

2016-02-24

国家自然科学基金资助项目(51675491)

李海广(1975—) ，男，副教授，博士研究生，主要从事信号处理、故障诊断技术研究。E-mail：btlhgboy@163.com

TJ25

A

1673-6524(2016)04-0082-05