近似梯度引导的人工蜂群搜索策略*

谢 娟，苏守宝，汪继文

1.安徽建筑大学 数理学院，合肥 230601

2.金陵科技学院 计算机学院，南京 211169

3.安徽大学 计算机科学与技术学院，合肥 230601

近似梯度引导的人工蜂群搜索策略*

谢 娟1，苏守宝2+，汪继文3

1.安徽建筑大学 数理学院，合肥 230601

2.金陵科技学院 计算机学院，南京 211169

3.安徽大学 计算机科学与技术学院，合肥 230601

XIE Juan,SU Shoubao,WANG Jiwen.Search strategy of artificial bee colony algorithm guided by approximate gradient.Journal of Frontiers of Computer Science and Technology 2016,10(12)：1773-1782.

针对人工蜂群算法自身存在的局部搜索能力较差，收敛较慢，易受到局部最优束缚的问题，在种群搜索过程中引入梯度信息，并利用中心差分格式对梯度做近似处理，提出了一种基于种群的梯度搜索策略，并用于人工蜂群算法采蜜蜂阶段的搜索，提高算法的局部搜索能力。同时，侦察蜂采用了全局随机搜索策略，以避免在解决多峰问题时，由于快速收敛而导致的早熟现象。在6个标准测试函数上的仿真实验结果表明，这种新的搜索机制在局部求解与全局探索之间取得了较好的平衡，使得改进后的算法在不同类型问题上的优化能力有了明显改善。

人工蜂群算法；近似梯度；局部搜索；合作与共享

1 引言

人工蜂群算法（artificial bee colony algorithm，ABC）是由土耳其学者Karaboga于2005年提出的一种基于蜂群智能行为的启发式优化算法[1]。ABC算法通过对蜂群个体之间在觅食过程中的劳动分工以及不同个体之间的信息共享机制——摇摆舞的模拟来实现对最优蜜源的选取。整个蜂群由采蜜蜂、观察蜂和侦察蜂3种类型的蜜蜂组成。采蜜蜂负责对巢穴周围的蜜源进行开采，记录每个蜜源的含密量及与巢穴的距离，通过摇摆舞的方式与巢穴周围的观察蜂共享蜜源信息，进而招募更多的观察蜂前去开采，以期发现更优质蜜源；在经过一段时间开采后，有些蜜源的质量无法得到进一步提高，则该蜜源将被抛弃，对应的采蜜蜂转变为侦察蜂，重新选择新的蜜源继续进行开采。相对于其他的群智能优化算法，ABC算法能够在局部搜索和全局探测之间做到较好的平衡，有效增加发现最优解的可能性，同时具有模型简单，参数少，易于理解，鲁棒性强的特点[2]，近年来受到国内外学者的广泛关注，并且在函数优化[3-4]、聚类分析[5]、图像处理[6-7]、负荷经济调度[8-9]等多个领域得到广泛应用。

在基本ABC算法中，采蜜蜂和侦察蜂负责在整个搜索范围内发现潜在最优解，即全局探测；而观察蜂是在“获取”采蜜蜂所共享的信息后，受优质蜜源的“招募”，对其进行进一步开采以提高最优解的质量，即局部搜索。ABC算法中的这种劳动分工机制导致了算法的局部搜索能力较弱，收敛较慢，尤其在解决多峰优化问题时，易出现早熟现象[10-11]。针对上述问题，国内外学者提出了不同的改进策略以提高其局部搜索能力，促进算法的全局优化能力的提升。Zhu等人将当前全局最优解引入ABC算法的搜索策略中，提出GABC（Gbest-guided ABC）算法，在当前全局最优解的引导下，整个蜂群快速向其聚集，提高了算法的局部搜索能力和收敛速度[11]。Gao等人将差分进化的思想引入到ABC算法的搜索策略中，同时在种群的初始化中利用混沌及反向学习技术以提高种群初始化质量，提出了ABC/best/1和ABC/best/2算法[3]。然而，无论是GABC还是ABC/ best/1、ABC/best/2算法，其相似之处都在于将当前全局最优解引入蜜源的搜索策略，在优化过程中容易出现“早熟”现象，这一点在多峰问题中尤为明显。由于单一的搜索策略难以克服复杂多变的优化问题，Kiran等人集成了具有不同特征的搜索方程，针对不同类型的优化问题选择相应的搜索策略，提高解的质量和算法的鲁棒性[12]。然而，为了选择较好的搜索策略，需要对候选解的质量进行多次评价，增加了时间开销。韩建权等人将基于当前最优解的混沌局部搜索策略和基于当前最优解的自适应侦查策略分别用于观察蜂和侦察蜂的搜索策略，提高了人工蜂群算法的局部搜索能力，有效地避免了其陷入局部最优[13]。此外，其他学者也在此方面做了卓有成效的改进研究工作[14-17]，详细的内容可以参考最近国内外关于ABC算法的文献综述[18-19]。

梯度信息往往给出了其方向导数在某点处取极值的方向，将其与其他智能优化算法结合，如差分进化[20]、遗传算法[21]，提高了算法的优化能力。然而，可微性的要求限制了梯度信息在优化算法中的广泛应用。Kuo等人在2015年提出了一种新的基于种群的梯度进化优化算法（gradient evolution，GE）[22]。受GE算法的启发，本文将近似梯度的计算方法引入采蜜蜂阶段的搜索，提出了一种基于梯度信息的人工蜂群算法（gradient based artificial bee colony algorithm，GdABC），以改进ABC算法的局部搜索能力，提高算法的优化性能。其优势在于利用梯度具有方向性的特点，“引导”个体提高自身的局部搜索性能，从而进一步提高算法的局部搜索能力和收敛速度。

2 基本的人工蜂群算法

在ABC算法中，每一个蜜源表示优化问题的一个可行解，通常用一个D维向量xi表示：

其中NP为种群大小。蜜源（可行解）的优劣用适应度函数Fitness表示；参数trial记录了每个蜜源没有得到更新的次数；Limit给出了每个蜜源最多被更新的次数上限。一旦蜜源相应的trial值超过Limit，该蜜源将被抛弃。算法在种群初始化后，通过采蜜蜂、观察蜂和侦察蜂3个阶段的相互合作，反复迭代直至满足迭代终止条件为止。下面从采蜜蜂、观察蜂和侦察蜂3个阶段概述基本ABC算法。

ABC算法首选在整个搜索空间内初始化NP个蜜源xi，每个蜜源用一个D维向量表示。为每个蜜源xi分配一个采蜜蜂，依据策略（2）在其邻域内生成新的候选解vi：

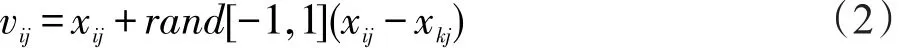
其中k∈[1,2,…,NP],k≠i，j∈[1,2,…,D]。评估两个蜜源的适应度值，采用贪婪选择机制，如果新的蜜源vi的适应度优于原有蜜源xi，则更新xi，triali置0；否则保留原有蜜源xi，triali加1。在所有采蜜蜂完成搜索之后返回信息共享区域，计算每个蜜源的适应度在所有蜜源中的百分比，如式（3）所示：

巢穴附近的观察蜂根据采蜜蜂所共享的蜜源信息（3），采用轮盘赌的方式选择相应蜜源，即采蜜蜂所在蜜源的适应度百分比越高，能招募到更多的观察蜂。观察蜂被招募之后，进而转变为采蜜蜂，仍然依据策略（2）在其邻域内进行搜索。

当每个蜜源的triali超过能够被评估的上限值Limit而解的质量仍未提高，则该蜜源将被抛弃，采蜜蜂转变为侦察蜂，按式（4）在搜索空间内重新生成新的蜜源。

其中xjmin、xjmax分别为第 j维方向上的最小和最大值。ABC算法的逻辑框架如下所示：

3 近似梯度引导下的人工蜂群算法

梯度能够引导算法的搜索快速指向可行解区域，有效地提高收敛速度。受GE算法的启发[22]，本文在ABC算法的采蜜蜂阶段引入梯度信息，提出基于梯度信息的采蜜蜂局部搜索策略。

采蜜蜂阶段的更新策略使个体从当前位置xt移动到下一个可能的位置xt+1(xt+1=xt+Δx)，优化函数f(x)在x+Δx处的泰勒级数展开为：

对式（5）两边取一阶导数，则有：

假设x+Δx处存在极值点，则 f′(x+Δx)=0，代入式（6）得：

利用牛顿-拉夫逊方法推导出下一个可能的位置xt+1可以表示为：

由中心差分公式对 f(x)的一阶和二阶导数做近似处理，最终可得对式（8）进行数值计算的中心差分格式：

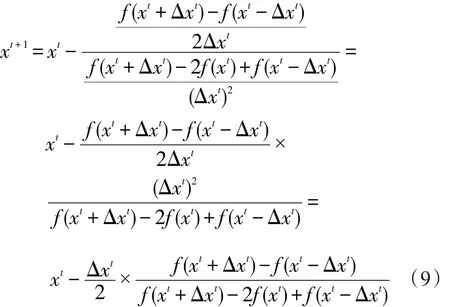
在采蜜蜂的搜索策略中，将梯度信息作为引导蜜源的移动方向，采用类似式的搜索方程[22]。然而，由于ABC算法是一个基于种群的搜索算法，直接采用式（9）会额外增加目标函数的计算，影响优化算法的效率，增加计算时间。因此在式（9）的基础上，结合GE算法的思想，给出适应于ABC算法搜索策略的梯度引导规则，主要包括以下几个方面（以最小化问题为例）：

在更新蜜源后，根据采蜜蜂所携带的蜜源信息招募观察蜂前往开采，仍然采用基本ABC算法中的更新规则（2）。当蜜源没有被更新的次数trial超过Limit，蜜源将被抛弃，重新按照式（4）生成新的蜜源。综上所述，本文提出的GdABC算法的逻辑框架如下所示：

4 仿真实验及结果分析

为了验证本文算法的有效性，选择了经典的6个标准测试函数来验证本文GdABC算法与基本ABC算法、GABC算法[11]在收敛精度、收敛速度等方面的比较。

4.1 标准测试函数

本文采用的6个基本测试函数如表1所示。

Table 1 Benchmark functions表1 标准测试函数

表1所给出的标准测试函数同时也是在其他文献中被广泛引用的[13,23]，F1～F6分别表示Sphere、Step、Schwefel、Rastrigin、Griewank和Rosenbrock测试函数。表1同时也给出了每个函数的类型：“U”表示仅有一个极值的单峰函数，主要用于对算法的收敛精度及速度的验证；“M”表示存在多个极值的多峰函数，用于对算法的全局优化能力的验证；此外，“S”、“N”分别表示优化函数的可分和不可分性。

4.2 实验参数设置及实验步骤

为了使实验的比较尽可能公平，本文采用了Karaboga在其网站公开的ABC算法的源码（http:// mf.erciyes.edu.tr/abc/publ.htm）。同时，作者对文献[11]提出的GABC算法重新编码，并依据文献中参数设置进行了验证。下面的实验中统一采用如下参数配置：种群大小为100，其中采蜜蜂和侦察蜂的数量各为50，参数Limit为100，以最大迭代次数作为循环终止条件。

4.3 实验结果及分析

仿真实验在30维，最大迭代次数1 000和60维，最大迭代次数3 000两种情况下分别独立运行30次。同时，采用Wilcoxon秩和检验，在置信水平为0.05时，对算法均值之间的显著性差异进行统计检验。表2和表3分别记录了每个算法在不同维数下的最优值、最差值、均值、方差及显著性差异。其中，在所比较的两个算法的sign值中，“+”表示前者与后者之间的差异显著，“－”表示两者差异不显著。图1～图12分别给出了3种算法（GdABC、GABC和ABC）在30维（图1～图6）和60维（图7～图12）下对6个标准测试函数的收敛曲线。

由上述实验结果可以得出如下结论：从收敛精度上看，由于GdABC算法利用梯度信息引导采蜜蜂的搜索，提高了算法的局部搜索能力。30次独立运行所得均值在30维情况下，GdABC算法在函数F1、F3、F4、F5的结果均优于其他两种算法，F2和F6上的结果不低于其他两种算法；在60维情况下，GdABC算法均优于其他算法。在0.05置信水平的假设检验结果亦表明GdABC算法在F1～F5上相对其他两种算法均表现出显著的差异性，而在F6上差异性不明显，这与本文的实验结果是一致的。

同时，由于侦察蜂仍采取全局随机搜索策略，在一定程度上减少了算法在优化多峰问题早熟的风险。此外，在收敛速度上看，图1～图12的收敛曲线反映出GdABC算法的收敛速度明显优于其他两种算法。

5 结束语

针对基本ABC算法本身存在的局部搜索能力较弱，收敛较慢的问题，将梯度信息引入采蜜蜂的搜索策略中，并采用中心差分公式对梯度做近似处理，提

高了算法的局部搜索能力。同时侦察蜂仍然采取随机的全局搜索策略，以保证算法仍具备较强的全局搜索能力。对6个典型标准测试函数的实验结果表明，GdABC算法能够较快地发现最优解，同时避免了多峰优化问题时易陷入局部最优的风险，整体优化性能有了较明显提高。

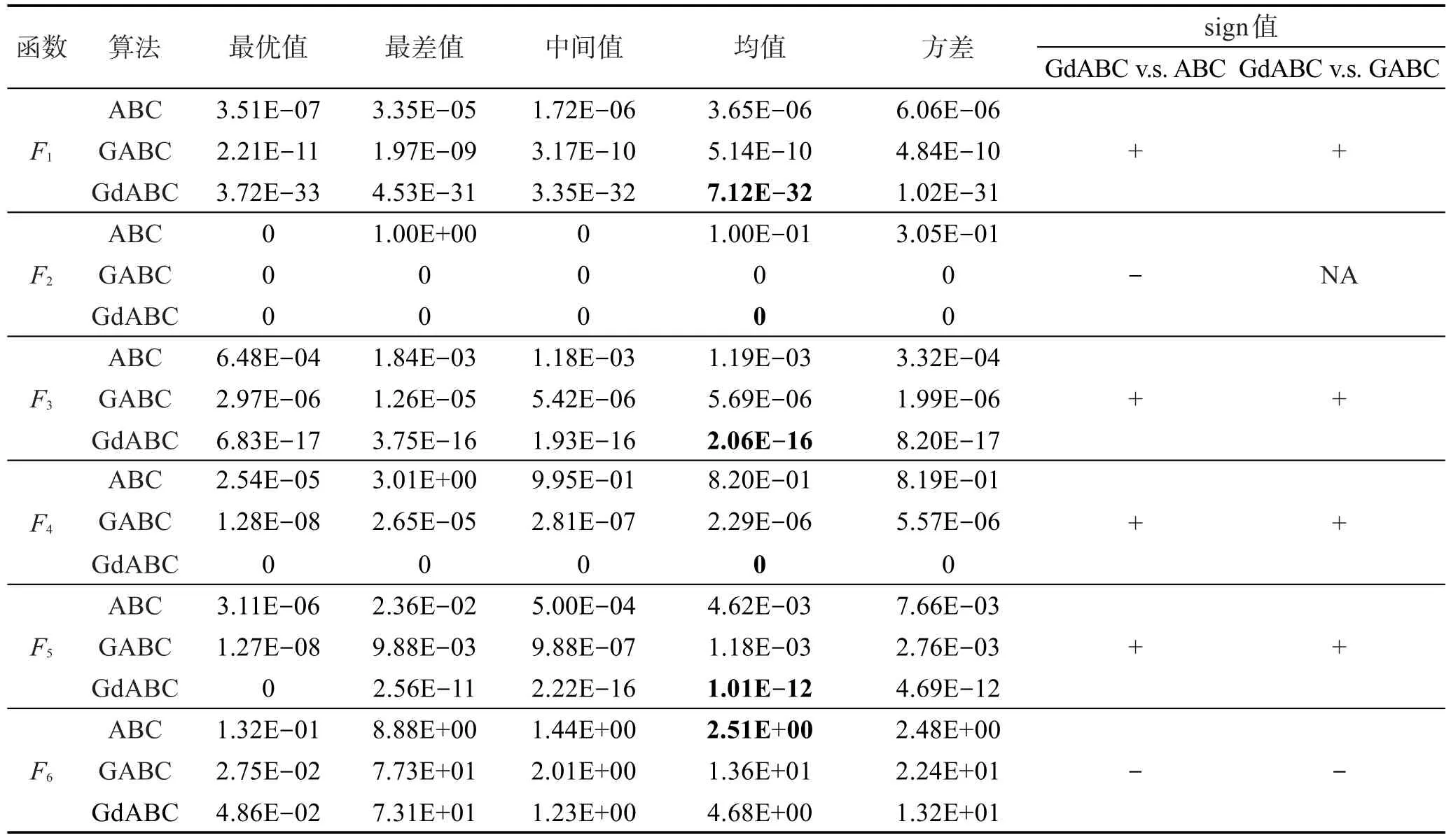
Table 2 Experiment results on three algorithms（Dim=30,Maxiteration=1 000）表2 3种算法在30维最大迭代1 000次下的实验结果

Table 3 Experiment results on three algorithms（Dim=60,Maxiteration=3 000）表3 3种算法在60维最大迭代3 000次下的实验结果

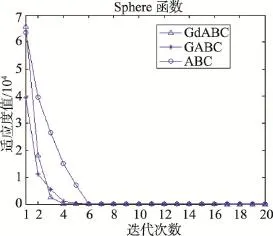
Fig.1 Convergent curve of Sphere function in 30 dimensions图1 Sphere函数在30维时的收敛曲线

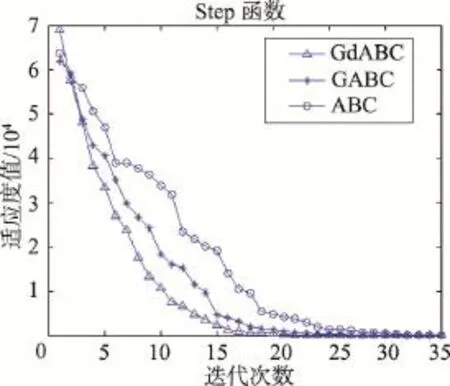
Fig.2 Convergent curve of Step function in 30 dimensions图2 Step函数在30维时的收敛曲线

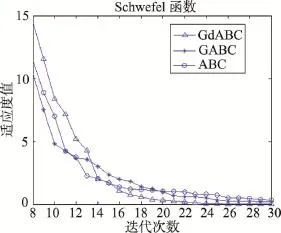
Fig.3 Convergent curve of Schwefel function in 30 dimensions图3 Schwefel函数在30维时的收敛曲线

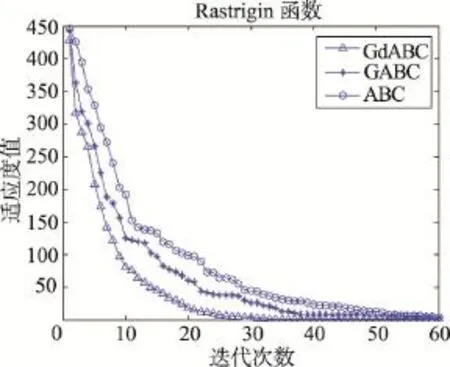
Fig.4 Convergent curve of Rastrigin function in 30 dimensions图4 Rastrigin函数在30维时的收敛曲线

Fig.5 Convergent curve of Griewank function in 30 dimensions图5 Griewank函数在30维时的收敛曲线

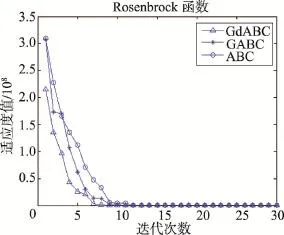
Fig.6 Convergent curve of Rosenbrock function in 30 dimensions图6 Rosenbrock函数在30维时的收敛曲线

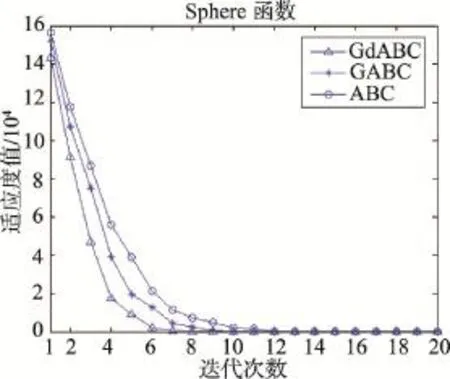
Fig.7 Convergent curve of Sphere function in 60 dimensions图7 Sphere函数在60维时的收敛曲线

Fig.8 Convergent curve of Step function in 60 dimensions图8 Step函数在60维时的收敛曲线

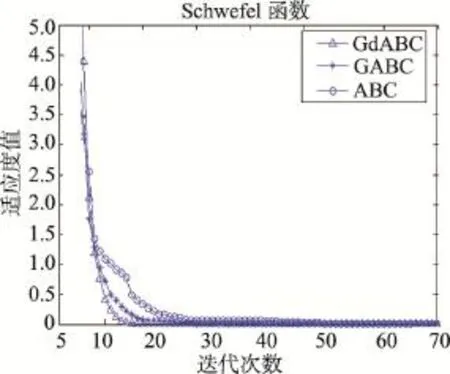
Fig.9 Convergent curve of Schwefel function in 60 dimensions图9 Schwefel函数在60维时的收敛曲线

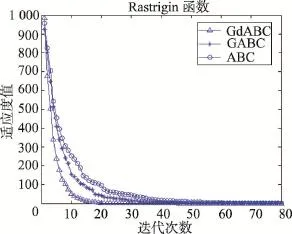
Fig.10 Convergent curve of Rastrigin function in 60 dimensions图10 Rastrigin函数在60维时的收敛曲线

Fig.11 Convergent curve of Griewank function in 60 dimensions图11 Griewank函数在60维时的收敛曲线

Fig.12 Convergent curve of Rosenbrock function in 60 dimensions图12 Rosenbrock函数在60维时的收敛曲线

[1]Karaboga D.An idea based on honeybee swarm for numerical optimization,TR06[R].Kayseri:Erciyes University,Engineering Faculty,Computer Engineering Department,2005.

[2]Gao Weifeng,Liu Sanyang.Improved artificial bee colony algorithm for global optimization[J].Information Processing Letters,2011,111(17):871-882.

[3]Gao Weifeng,Liu Sanyang,Huang Lingling.A global best artificial bee colony algorithm for global optimization[J]. Journal of Computational&Applied Mathematics,2012, 236(11):2741-2753.

[4]Tsai P W,Pan J S,Liao B Y,et al.Enhanced artificial bee colony optimization[J].International Journal of Innovative Computing Information&Control,2009,5(12):5081-5092.

[5]Tran D C,Wu Zhijian,Wang Zelin,et al.A novel hybrid data clustering algorithm based on artificial bee colony algorithm and K-means[J].Chinese Journal of Electronics,2015, 24(4):694-701.

[6]Draa A,Bouaziz A.An artificial bee colony algorithm for image contrast enhancement[J].Swarm and Evolutionary Computation,2014,16:69-84.

[7]Charansiriphaisan K,Chiewchanwattana S,Sunat K.Acomparative study of improved artificial bee colony algorithms applied to multilevel image thresholding[J].Mathematical Problems in Engineering,2013:17.

[8]Abro A G,Mohamad-Saleh J.Enhanced probability-selection artificial bee colony algorithm for economic load dispatch: a comprehensive analysis[J].Engineering Optimization, 2014,46(10):1315-1330.

[9]Bulut O,Tasgetiren M F.An artificial bee colony algorithm for the economic lot scheduling problem[J].International Journal of Production Research,2014,52(4):1150-1170.

[10]Li Guoqiang,Niu Peifeng,Xiao Xingjun.Development and investigation of efficient artificial bee colony algorithm for numerical function optimization[J].Applied Soft Computing, 2012,12(1):320-332.

[11]Zhu Guopu,Kwong S.Gbest-guided artificial bee colony algorithm for numerical function optimization[J].Applied Mathematics and Computation,2010,217(7):3166-3173.

[12]Kiran M S,Hakli H,Gunduz M,et al.Artificial bee colony algorithm with variable search strategy for continuous optimization[J].Information Sciences,2015,300:140-157.

[13]Han Jianquan,Mao Li,Zhou Changxi.Artificial bee colony algorithm based on improved local search strategy[J].Journal of Frontiers of Computer Science and Technology, 2015,9(6):761-767.

[14]Tang Lingyun,Mao Li,Zhou Changxi.Improved artificial bee colony algorithm for function optimization[J].Journal of Frontiers of Computer Science and Technology,2015,9 (7):854-860.

[15]Xie Juan,Qiu Jianfeng,Min Jie,et al.Improved artificial bee colony algorithm with dual cognitive abilitied and performance analysis[J].Computer Science,2014,41(11):269-272.

[16]Zhou Xinyu,Wu Zhijian,Deng Changshou,et al.Neighbour search-based artificial bee colony algorithm[J].Journal of Central South University:Science and Technology, 2015,46(2):534-546.

[17]Zang Peiquan,Sun Chen’ao,Gu Xiaofeng,et al.An artificial bee colony bee colony algorithm with adaptive chemotaxis and guiding factors[J].Computer Engineering and Science,2015,37(9):1692-1697.

[18]Qin Quande,Cheng Shi,Li Li,et al.Artificial bee colony algorithm:a survey[J].CAAI Transactions on Intelligent Systems,2014,9(2):127-135.

[19]Karaboga D,Gorkemli B,Ozturk C,et al.A comprehensive survey:artificial bee colony(ABC)algorithm and applications[J].Artificial Intelligence Review,2014,42(1):21-57.

[20]Ibtissem C,Nouredine L.A hybrid method based on conjugate gradient trained neural network and differential evolution for non linear systems identification[C]//Proceedings of the 2013 International Conference on Electrical Engineering and Software Applications,Hammamet,Mar 21-23, 2013.Piscataway,USA:IEEE,2013:1-5.

[21]Du Tingsong,Fei Pusheng,Shen Yanjun.A modified niche genetic algorithm based on evolution gradient and its simulation analysis[C]//Proceedings of the 3rd International Conference on Natural Computation,Haikou,Aug 24-27,2007. Piscataway,USA:IEEE,2007:35-39.

[22]Kuo R J,Zulvia F E.The gradient evolution algorithm:a new metaheuristic[J].Information Sciences,2015,316:246-265.

[23]Cao Chunhong,Xu Guangxing.Geometric constraint solvingbased on improved artificial bee colony algorithm[J].Journal of Frontiers of Computer Science and Technology,2015, 9(9):1122-1131.

附中文参考文献：

[13]韩建权,毛力,周长喜.基于改进局部搜索策略的人工蜂群算法[J].计算机科学与探索,2015,9(6):761-767.

[14]唐凌芸,毛力,周长喜.求解函数优化问题的改进人工蜂群算法[J].计算机科学与探索,2015,9(7):854-860.

[15]谢娟,邱剑锋,闵杰,等.具有双重认知能力的人工蜂群算法及性能分析[J].计算机科学,2014,41(11):269-272.

[16]周新宇,吴志健,邓长寿,等.一种邻域搜索的人工蜂群算法[J].中南大学学报:自然科学版,2015,46(2):534-546.

[17]臧培荃,孙晨骜,顾晓峰,等.具有自适应趋向性和引导因子的人工蜂群算法[J].计算机工程与科学,2015,37(9): 1692-1697.

[18]秦全德,程适,李丽,等.人工蜂群算法研究综述[J].智能系统学报,2014,9(2):127-135.

[23]曹春红,许光星.基于改进人工蜂群算法的几何约束求解[J].计算机科学与探索,2015,9(9):1122-1131.

XIE Juan was born in 1980.She received the M.S.degree from Anhui University in 2007.Now she is an associate professor at Anhui Jianzhu University.Her research interests include intelligent optimization algorithm,evolutionary computing and machine learning,etc.

谢娟（1980—），女，安徽淮北人，2007年于安徽大学获得硕士学位，现为安徽建筑大学副教授，主要研究领域为智能优化算法，进化计算，机器学习等。

SU Shoubao was born in 1965.He received the Ph.D.degree from Anhui University in 2009.Now he is a professor and M.S.supervisor at Jinling Institute of Technology,and the senior member of CCF.His research interests include swarm intelligence,big data computing and embedded control optimization,etc.

苏守宝（1965—），男，安徽六安人，2009年于安徽大学获得博士学位，现为金陵科技学院教授、硕士生导师，CCF高级会员，主要研究领域为群智能，大数据计算，嵌入式控制优化等。

WANG Jiwen was born in 1958.He received the Ph.D.degree from University of Science and Technology of China in 2001.Now he is a professor and Ph.D.supervisor at Anhui University.His research interests include intelligent computing and machine learning,etc.

汪继文（1958—），男，安徽宿松人，2001年于中国科学技术大学获得博士学位，现为安徽大学教授、博士生导师，主要研究领域为智能计算，机器学习等。

Search Strategy of Artificial Bee Colony Algorithm Guided by Approximate Gradient*

XIE Juan1,SU Shoubao2+,WANG Jiwen3
1.School of Mathematics&Physics,Anhui Jianzhu University,Hefei 230601,China
2.School of Computer,Jinling Institute of Technology,Nanjing 211169,China
3.School of Computer Science&Technology,Anhui University,Hefei 230601,China
+Corresponding author:E-mail:showbo@jit.edu.cn

To solve the problems of inferior local search ability,slow convergence and easily trapping into the local optimization existing in the artificial bee colony algorithm,this paper proposes a gradient search strategy based on population by introducing gradient information and using central difference schemes for gradient approximation processing.The novel search strategy used by employed bees improves the local search ability while the scout bees still employ global random searching strategy to avoid premature phenomenon led by fast convergence in solving multimodal problems.Simulation results in six standard test functions show that the proposed searching mechanism gives a good balance between local solution and global exploration and improves the optimization ability of differentkinds of optimization problems.

artificial bee colony algorithm;approximate gradient;local search;cooperation and sharing

10.3778/j.issn.1673-9418.1601072

A

TP301.6

*The National Natural Science Foundation of China under Grant No.61375121(国家自然科学基金);the Provincial Projects of Natural Science for Anhui Universities under Grant No.KJ2013A009(安徽高校省级自然科学研究项目);the Doctoral Scientific Research Foundation of Anhui University(安徽大学博士启动基金);the Scientific Research Program for Introducing Talents of Jinling Institute of Technology under Grant No.jit-rcyj-201505(金科院引进人才科研项目).

Received 2016-01,Accepted 2016-04.

CNKI网络优先出版:2016-04-01,http://www.cnki.net/kcms/detail/11.5602.TP.20160401.1614.006.html