探究性学习的体会
2016-12-19 08:19:44湖北张奕昕
高中数理化 2016年23期
◇ 湖北 张奕昕
探究性学习的体会
◇ 湖北 张奕昕
平面向量题是高考重点考查的知识题型,由于其具有代数与几何双重身份,在小题考查中相对有一定难度.本文通过对一道向量高考题的多角度分析,使考生明确向量问题求解途径.

1 利用平面几何性质,转化向量内涵
平面向量中的很多问题都有着其特定的几何背景,充分利用向量的几何模型,是解决向量问题的常用手段和重要策略.
解法1 由题意得点B1、B2在以O为圆心的单位圆上.点P在以O为圆心、半径为1/2的圆内.又所以点A在以B1B2为直径的圆上.当P与点O重合时最大,最大值为当P在圆周上时,最小,最小值为
2 借助坐标运算,化抽象为具体
坐标化思想是处理向量问题的有力工具,其特征就是利用坐标形式将向量问题代数化,简化思维量.其核心是准确确定向量的坐标.
解法2 根据条件知A、B1、P、B2构成一个矩形,以AB1、AB2所在直线为坐标轴建立如图1所示平面直角坐标系.设|AB1|=a,|AB2|=b,则点O(x,y)、P(a,b).

图1
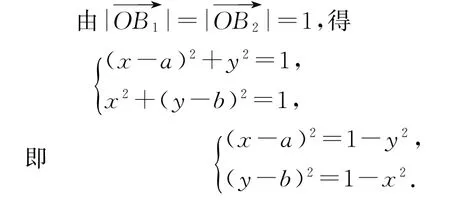
所以1-x2+1-y2<1/4,即

因为(x-a)2+y2=1,所以
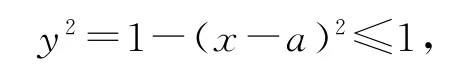
即y2≤1.同理x2≤1,所以

由式①、②知7/4<x2+y2≤2.因为
3 借助临界分析,突显几何直观
对于向量关系错综复杂的问题,需要挖掘这些关系,将问题表征成直观形象的图形来简洁求解.
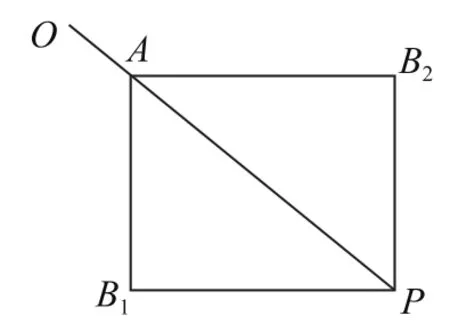
图2
同理可判断段AP的延长线上时,与题意不符.故可确定点O在线段AP上.


图3
设O1A=x,在△OO1B1中,O1B1=x,OO1=x-1/2,OB1=1.由勾股定理即解得(另一值舍去).
以上视角可以帮助我们更好地思考和理解向量本质,顺利解决向量的综合问题.
(作者单位:湖北武汉市第二中学)
猜你喜欢
福建中学数学(2023年5期)2024-01-25 17:41:36
中学生数理化·八年级物理人教版(2023年11期)2023-12-26 07:50:04
动漫界·幼教365(大班)(2023年3期)2023-05-02 06:35:26
动漫界·幼教365(中班)(2023年3期)2023-04-23 08:31:29
河北理科教学研究(2021年4期)2021-04-19 13:34:48
数学年刊A辑(中文版)(2021年4期)2021-02-12 01:21:04
科学(2020年1期)2020-08-24 08:08:06
新教育(2018年8期)2018-08-29 00:53:20
中等数学(2018年1期)2018-08-01 06:41:04
应用数学与计算数学学报(2015年1期)2015-07-20 11:39:06

