非合作目标姿态测量的嵌入式算法
吴 斌,叶 东,张 鑫,赵振庆
(哈尔滨工业大学 电气工程及其自动化学院,黑龙江 哈尔滨 150001)
非合作目标姿态测量的嵌入式算法
吴 斌,叶 东*,张 鑫,赵振庆
(哈尔滨工业大学 电气工程及其自动化学院,黑龙江 哈尔滨 150001)
针对一系列含有圆和直线特征的航天器,提出了基于嵌入式算法来实现非合作目标的姿态测量。该算法在现场可编程门阵列(FPGA)中完成边缘点的检测和边缘图像的细化;在数字信号处理器(DSP)中通过基于弧段的快速椭圆检测方法检测目标上的椭圆特征;同时用快速高精度的二次Hough直线检测方法检测目标上的直线特征。最后,针对实际在轨任务进行了地面模拟实验,基于椭圆特征和直线特征计算了目标飞行器和一个CCD相机的相对姿态。结果显示:该嵌入式方法所需资源较少,更新率优于3 Hz;其测量精度随着测量距离的变大而变差,同一距离3个方向的测量精度不同,近距离(小于4 m)、深度方向的测量精度优于100 mm,其他方向最高优于60 mm,角度精度优于1°,满足嵌入式系统对资源、在轨更新率和精度的要求。
计算机视觉;非合作目标;姿态测量;椭圆检测;二次Hough变换
1 引 言
随着空间技术的发展,空间飞行器交会对接、在轨维修和维护等在空间计划和任务中扮演着越来越重要的角色,已经成为空间活动不可或缺的重要组成部分。在空间交会对接、在轨服务等航天任务的最后逼近阶段,通常采用光学成像敏感器来测量追踪航天器与目标航天器之间的相对位置和姿态。最初采用的测量方式是合作目标的方式[1-3],即在目标航天器上放置特定的光学靶标,通过识别靶标来测量追踪航天器与目标航天器之间的相对位置和姿态。但这种方式只能对装有目标识别器的航天器进行测量。因此,相关研究人员又提出了针对非合作目标的相对位姿测量方法,其可对没有安装目标识别器的非合作目标航天器进行相对位姿测量。非合作目标的相对位姿测量方法已广泛地应用于传统航天器的在轨维护、太空垃圾清理以及军事目标的空间攻防等方面[4]。
C.Miravet[5]利用形态学方法在地球背景下提取出目标航天器的外轮廓,进而粗略计算航天器的姿态,这种方法精度不高,适用于远距离估算;Fuyutot[6]将航天器外形进行重构,从而得到当前航天器的姿态,这种方法计算速度慢、资源消耗高,难以在轨和嵌入式实现;Chien[7]通过匹配模板得到航天器的姿态,需要较大的存储空间;徐文福[8]等提取航天器上的直线交点作为计算特征点,再通过双目视觉得到目标航天器的姿态,直线容易被遮挡,同时基于点的双目视觉测量精度受相机之间的基线限制,测量距离有限;苗锡奎[9]等通过提取航天器星箭对接环的圆形特征,利用单目视觉计算目标航天器的姿态,然而文章并没有介绍椭圆提取这一关键性步骤,而且其解决姿态的二义性需要额外已知一个点的空间坐标。
圆形物体常见于人造航天器的对接装置上,其在像面上的投影一般呈椭圆形,是较易于计算的特征。相对于点、线特征,圆特征具有抗干扰(遮挡、光照)能力强、提取的特征少等优点。然而,准确地提取椭圆是一个比较具有挑战性的任务。一般来说椭圆提取方法主要有3种:拟合方法、Hough变换、基于弧段提取的方法。拟合方法提取椭圆时大多基于最小二乘方法[10-12],由于这类方法要求所有参与计算的点都要在同一个椭圆上,通常不能单独使用。Hough[13-15]变换方法对椭圆检测有着较强的抗噪声能力,然而这种方法计算速度慢并且需要大量的存储空间,因此难以满足计算速度的要求和嵌入式实现。基于弧段提取的椭圆检测方法[16-18]首先基于连续性、凹凸性、椭圆几何特征等将属于同一椭圆上的弧段聚类,然后利用这些弧段计算椭圆的参数。这是一种快速有效的检测方法,是目前椭圆检测研究的主要方向。
本文提出一种将圆形和直线特征相结合的快速姿态测量方法,首先利用基于弧段的椭圆检测算法检测椭圆,利用椭圆计算目标的姿态参数(圆心位置和圆所在平面的法线方向),然后利用提取的直线参数解决姿态计算的二义性问题,得到正确的姿态参数。相比于现有的一些方法,本文算法无需额外的辅助设备就可以解决利用单目椭圆特征计算姿态产生的二义性,并且兼顾了实际应用时嵌入式系统的资源、计算速度等一系列现实要求。本文不仅对算法进行了仿真实验,并且实现了算法的嵌入式,针对实际在轨任务进行了地面模拟实验。
2 本文算法流程
本文算法流程图如图1所示。

图1 算法框图
由于构成椭圆的弧段是光滑、无分叉的,本节通过以下几个步骤检测弧段:首先,在原图上进行边缘检测,得到边缘图像;然后,对边缘图像进行基于形态学的边缘细化,获得单像素边缘;再通过改进的链码算法连接相邻的边缘点得到无分叉的弧段;最后,采用一种新的快速的弧段分割方法处理得到光滑的弧段。
2.1 边缘提取与细化


图2 需删除的边缘点及其邻域举例(数字是查询表的索引)
Fig.2 Illustration of edge points that should be removed
接下来需要对边缘图像进行边缘细化,边缘细化可以得到单像素边缘,是后续算法实现的前提。为了快速实现细化,本文采用查询表的方式,表中列出了需要删除的边缘点周围八邻域像素排列的所有可能情况[19],通过比较当前边缘点周围八邻域像素和表中对应的位置,删除不必要的边缘点,从而得到单像素边缘。图2列出了细化过程中需要删除的边缘点周围八邻域排列的几种可能。
2.2 弧段提取与移除
为了能够提取无分叉的弧段,本文提出一种改进的链码算法用于弧段提取。即在标准链码检测方法的基础上加入了一个约束条件:对于某个弧段上的点,如果其周围八邻域像素内含有的边缘点大于2,则弧段在该点断裂。如图3,值得注意的是,该方法使用的前提是边缘细化,如果没有进行边缘细化,这种方法将产生大量错误的断裂点。
经过弧段提取之后,需要删除两类不是椭圆上的弧段以提高计算速度。第一类是非常短的弧段,这类弧段容易被噪声影响;第二类是直线度较高的弧段,这类弧段极大可能是直线而不是椭圆上的弧段。本文定义此节被删除的边缘点集为Pr,图像上所有边缘点集为Pw,显然Pr⊆Pw。

图3 简单约束下快速弧段提取
2.3 弧段分割
由于2.2节并不能保证弧段上的点都是椭圆上的点,如图4(彩图见期刊电子版)所示,显然该弧段只包含了一部分椭圆上的点。由于椭圆上的曲率变化是连续、平稳的,因此需要得到光滑的弧段,该弧段在任意一点上的曲率都不会发生突变。当弧段上某个点处的曲率发生了突变,则可以认为该点是分割点。
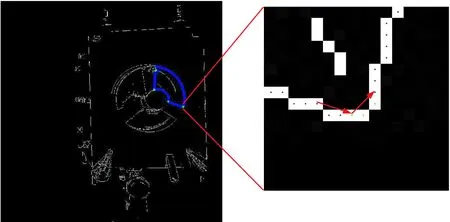
图4 弧段上得到的分割点(蓝色的点是经过2.2节得到的一条弧段上的边缘点;绿色的点是分割点;红色带箭头的线段代表其中一个分割点处的向量)
Fig.4 Segmentation points on the arcs(blue points are edge points extracted in section 2.2, green points are inflexion points, red line segments with arrows are vector)

3 椭圆检测
在弧段检测之后,根据椭圆及光滑弧段的性质将位于同一椭圆上的弧段聚类,每一类弧段对应一个椭圆。
本文提出两种弧段约束聚类方法:凹凸性约束和拟合误差约束。凹凸性约束提供了一种简单快速的方法判断两条弧段是否可以聚类,是聚类的必要不充分条件。最小拟合误差约束依据的是椭圆的基本性质,是两条弧段是否属于同一椭圆的决定性约束。相对于凹凸性约束,拟合误差约束的计算量较大。因此本文首先通过凹凸性约束快速去除一些不可能的聚合情况,然后采用最小拟合约束进行最终聚类。
3.1 凹凸性约束
给定两条弧段P=(p1,p2,…,pm)和Q=(q1,q2,…,qn)。分别计算得到两条弧段的中点Cp和Cq,连接Cp和Cq得到线段l1;连接弧段P的首末端点p1、pm得到线段l2,连接弧段Q的首末端点q1、qn得到线段l3。那么P和Q可以聚类当且仅当条件1成立。
条件1:l1和l2相交并且l1和l3相交。

图5 凹凸性约束
图5是两条弧段的相对位置的4种情况,显然只有第一种情况下两条弧段才可能属于同一个椭圆。
3.2 拟合误差约束
如上给定的两条弧段P和Q,对两条弧段上所有的边缘点进行椭圆拟合,拟合误差E可表示为式(1):
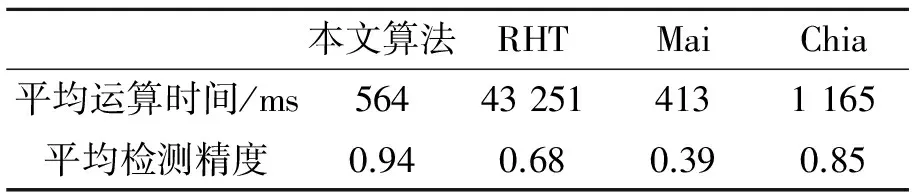
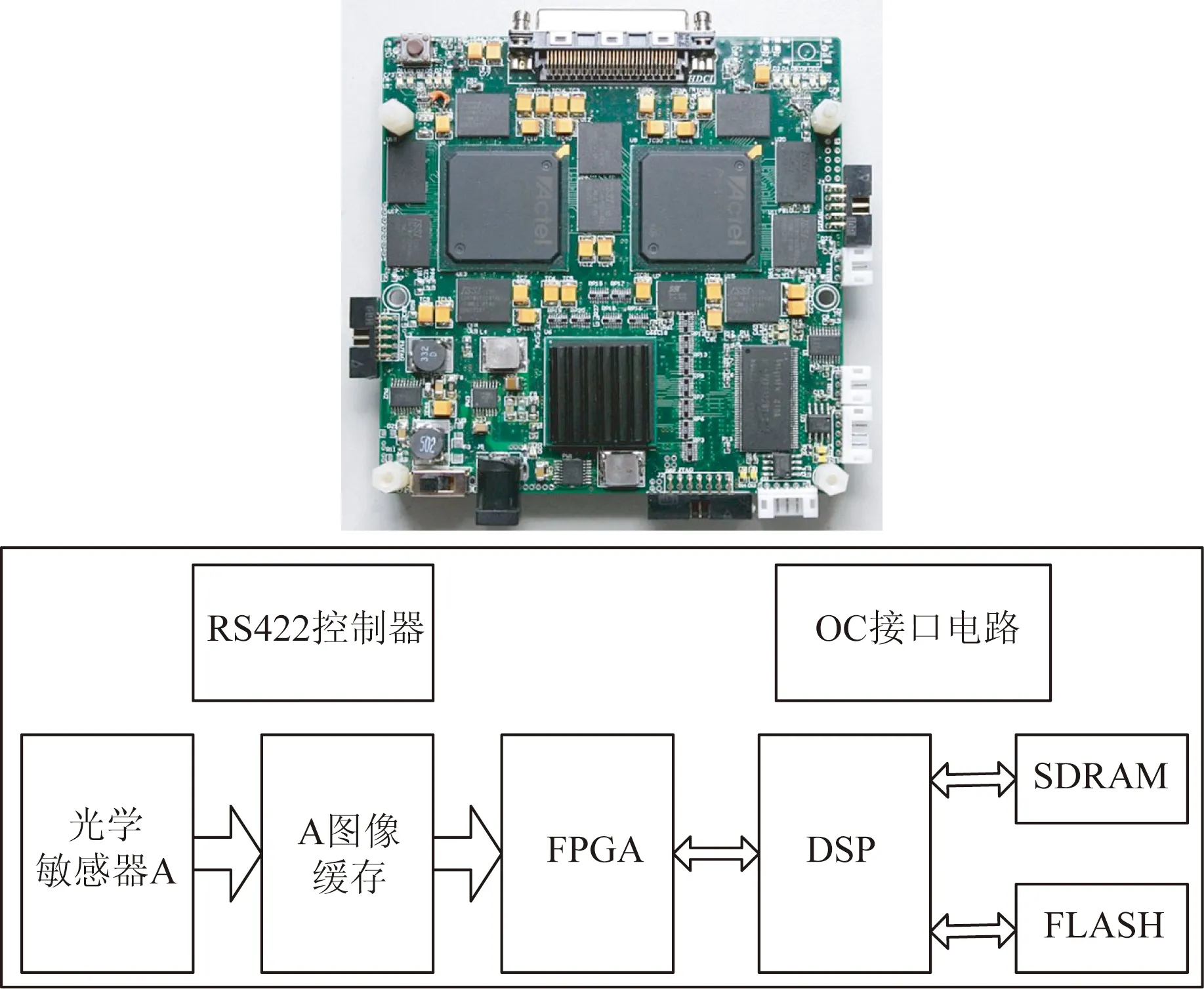
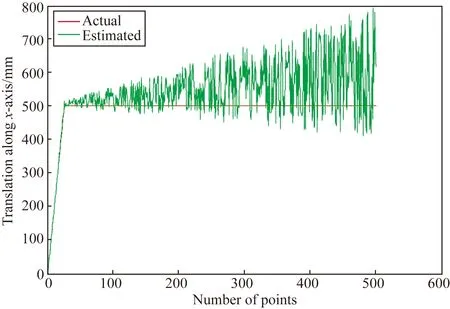
E (1) 其中:e0表示能够接受的最大误差,M表示两条弧段上所有边缘点的数量,N表示两条弧段上满足拟合椭圆的边缘点的数量。显然E越小,效果越好,两条弧段越有可能属于同一椭圆。本文取e0为0.1。 考虑到基于椭圆的单目视觉姿态解算只能得到目标的5个姿态参数,缺少滚转角,本文通过检测直线、依据直线的参数确定最后一个姿态角。 目前最常用的直线检测方法是Hough变换,通过提高Hough空间分辨率理论上可以得到极高的精度,但是这也会带来沉重的计算负担和巨大的存储需求。例如,在实际项目中相机获取的图片分辨率为2 048×2 048,在像素级Hough提取精度下的Hough空间大小为:(8 193+2)×(180+2)个16位数据,如果要实现更高精度比如十倍精度,Hough空间将是上述大小的十倍。因此,高精度的Hough变换难以在嵌入式系统中实现。针对这种情况,本文提出了一种分层高精度直线提取方法,完成Hough变换直线提取的嵌入式实现。 算法的第一层是像素级Hough变换初提取。为了能够在整个图像中提取任意直线,同时限制Hough空间的大小,这层算法采用像素级Hough变换进行直线初提取。使用2.2节中的边缘点集Pr代替整个图像的边缘点集Pw作为本层输入,以提高第一层的计算速度。通过本层计算,能够得到图像中的直线参数,但是提取精度只有像素级边缘图像。 算法的第二层是二次高精度Hough变换。本层从两个方面降低Hough变换需要的存储空间和计算量:减少Hough变换的输入边缘点、缩小Hough空间。具体步骤如下:给定第一层得到的直线参数为(ρ,θ)。首先,寻找第一层得到直线附近的边缘点集Ps⊆Pr,将其作为第二层计算的输入边缘点,进一步减少Hough的计算量,Ps可由算法1得到,其中e0是允许的最大误差。然后,在第一层计算得到的直线参数邻近区域进行第二层Hough变换,其空间大小如式(2): lρ×lθ=(2RρSρ+1)×(RθSθ+1), (2) 其中:RρRθ表示对第一层计算结果ρθ的不信任程度,不信任程度越高,第二层Hough空间越大,SρSθ表示了第二层Hough空间的精度,SρSθ越大,得到的直线参数精度越高,第二层Hough空间越大,计算时间越长。第二层Hough空如图6所示。 图6 第二层Hough空间 算法1 计算直线附近的边缘点,输入:直线参数(ρ,θ)及边缘点集Pr,输出:边缘点集Ps For all pointspi(xi,yi)∈Prdo e=xicosθ+yisinθ-ρ Ife EnterpiintoPs End if End for 本文算法可以应用于一类含有圆形和直线特征的航天器模型,如图7。其中,依据图像上的椭圆特征可以计算姿态参数[20],而利用直线特征可以解决姿态的二义性。 图7 航天器模型与坐标系 5.1 基于圆的单目姿态解算 如果已知空间圆的半径R,仅仅利用单目视觉即可计算空间圆的姿态。其算法原理为:空间圆及其投影到图像上的椭圆均位于以相机原点为顶点的空间圆锥上,所以用平面和圆锥相交,截面为圆并且半径为R即可确定圆的空间姿态。算法主要由以下几步实现: (1)得到空间圆锥方程。设从图像中提取的椭圆方程为: a′u2+2h′uv+b′v2+2g′u+2f′v+d′=0. (3) 由小孔成像原理: (4) 其中fc为相机的焦距。 将式(4)带入式(3),可得空间圆锥方程为: ax2+by2+cz2+2fyz+2gzx+2hxy=0, (5) 其中: (2)得到空间圆锥的标准形式,对系数矩阵: (6) 进行特征值分解,通过特征向量构成的正交矩阵P将(5)化为标准形式: λ1x′2+λ2y′2+λ3z′2=0, (7) 其中:λ1,λ2,λ3是系数矩阵Q的特征值。 (3)得到标准坐标系下的姿态。圆心位置为: (8) 圆平面法线为: (9) (4)得到摄像机坐标系下姿态。将标准坐标系转换到摄像机坐标系下: (10) (11) 5.2 基于直线消除多解 由上节结果可知,基于椭圆的单目视觉姿态解算会产生两个解,实际上只有当空间圆平面垂直于相机光轴时,才能唯一确定一个解。本节利用航天器上两对平行直线的图像确定圆平面的法线方向,从而确定空间圆的唯一姿态。 图7所示的航天器外轮廓上一对平行直线,可由第4节方法快速提取,设其齐次坐标为: L1=(l1,m1,n1)T,L2=(l2,m2,n2)T. (12) 其对应的影消点可由这两条直线的交点得到: v1=L1×L2. (13) 则在相机坐标系下这两条平行直线的方向为: d1=K-1v1, (14) 其中,K为摄像机内参矩阵。 同理可得到另外一对平行线的方向为: d2=K-1v2. (15) 最终,在相机坐标系下空间圆平面的法线方向为: n=d1×d2. (16) 本文算法中椭圆提取是至关重要的部分,因此本文实验分为两个部分:椭圆提取实验与姿态测量实验。 6.1 椭圆检测实验结果 为了验证椭圆检测算法的有效性,建立了基于VC的算法仿真系统,对一些真实图像进行处理、检测椭圆并和其他椭圆检测算法进行比较。因为本文算法是基于弧段的椭圆检测算法,本文选择Mai等[16]和Chia等[17]方法作为比较算法。此外,应用最广泛的椭圆检测算法:随机Hough变换(RHT)[22]也被选择作为比较算法。 真实图像来源于本文的太空模拟实验,包含400幅由同一航天器在不同距离、不同光照、不同姿态下拍摄的图片(2 048 pixel×2 048 pixel)。如图8。 图8 不同情况下实验图片 依据检测到的椭圆Ed内部区域Rd和真实椭圆Et内部区域Rt的重合程度评价检测精度p: (17) 其中:Nb表示既属于区域Rd又属于Rt的像素的数量,是Rd和Rt的交集,Nt表示区域Rd和Rt内所有像素的数量,是Rd和Rt的并集。 本实验在PC(Core i7-860)中实现,结果如表1所示。由表1可见:RHT算法耗时最长,一般情况下不采用这种方法检测椭圆;Mai算法虽然计算速度最快,但是计算精度很差,这是因为这种算法中缺少对拐点的处理,无法删除错误弧段;RHT、Chia算法无论从计算速度还是精度方面都不如本文算法。 表1 椭圆检测效果 6.2 姿态测量嵌入式实验 本文算法的目的是在嵌入式系统中实现航天器姿态测量,故在嵌入式系统中实现了本算法,并设计了模拟航天器在太空中姿态变化的地面测试系统。 6.2.1 系统组成 地面测试系统主要包括姿态测量嵌入式系统、航天器模型、CCD摄像机、六自由度运动系统以及测试比较系统。 嵌入式系统具有高度集成化、低重量、小尺寸、低功耗等特点,用于完成光学相机图像数据采集、椭圆和直线特征检测、目标姿态解算、数据发送等功能。硬件实物及其原理图如图9,为了更好地利用硬件资源、加快嵌入式运算速度,边缘提取和细化在FPGA中实现,其他算法在DSP中运行。 图9 嵌入式系统 航天器模型和真实航天器按照1∶2比例加工,见图10。加工精度为0.01 mm,航天器主体是1 m×1 m×1 m的立方体,喷管直径为125 mm(内圈小圆),对接环直径为450 mm(外圈大圆),上面有加强筋、星敏模型等。 图10 卫星实物模型 六自由度运动系统见图11,其可提供相对运动的真值。其平移量和旋转量通过激光测距、光栅尺等内部设备测出。该系统的两个运动部件可以做水平、竖直、深度三维方向相对平移,以及俯仰、偏航、滚转三个自由度相对旋转。系统参数为:水平及竖直平移范围:±0.5 m;深度方向平移范围:0.1~15 m;俯仰和偏航旋转范围:±60°;滚转旋转范围:360°。 图11 运动系统与实验环境 CCD摄像机分辨率为2 048×2 048,焦距为10.02 mm,主点位置为(1 005.07, 1 029.84),像元大小为0.015 mm×0.015 mm。 测试比较系统通过RS422串口分别从姿态测量嵌入式系统和六自由度测试系统中传出数据到电脑主机中,实时比较测量效果。 将CCD摄像机和目标航天器模型分别固定于六自由度测试系统上,它随着六自由度运动系统做运动,从而实现CCD摄像机和目标模型的相对运动。CCD摄像机、目标航天器模型和六自由度运动系统的相对关系由激光跟踪仪标定。当CCD摄像机和目标航天器模型随着六自由度运动系统运动时,它们之间相对位姿的准确值可以由六自由度运动系统给出的值可经过坐标系变换得到。 6.2.2 试验过程及结果 为了模拟太空环境,本文所有实验均在搭建的光学暗室中进行,如图11。CCD摄像机和目标航天器模型的距离不同时,单位像素代表的实际尺寸不同,因此姿态测量精度主要受到测量距离的影响,实验将验证姿态测量精度和距离的关系。实验分为两类:静态定点测量和动态测量。 静态定点测量。CCD摄像机和目标航天器模型间的距离范围是0.5~10 m,每隔0.5 m进行一组定点测量,在相机可见目标范围内随机选择20个位置进行静态测量,总共有400个位置,将每组测量的最大误差作为这组精度的描述指标。静态定点测量能够避免数据不同步,保证嵌入式系统测量得到的姿态和六自由度系统给出的姿态是同一个位置。测量结果如图12,在近距离时(小于4 m)能够达到:深度方向平移误差优于100 mm,非深度方向平移误差优于60 mm,角度旋转测量误差优于1°。这个测量误差随着测量距离的变大而变大。 图12 静态测量位置误差和角度误差 动态测量。设计了一系列的CCD摄像机和目标航天器模型之间的相对运动:由近及远实验模拟航天器之间的分离、由近及远实验模拟航天器之间的对接。图13是动态测量分离实验举例,初始状态CCD摄像机和目标航天器模型的相对姿态为:x方向Tx=0 mm、y方向Ty=0 mm、z方向Tz=500 mm、绕x轴旋转ψ=0°、绕y轴旋转θ=0°、绕z轴旋转φ=0°,以0.2 m/s的位移速度、0.5 (°)/s的角度旋转速度运动到:Tx=500 mm、Ty=-500 mm、Tz=10 000 mm、ψ=60°、θ=45°、φ=30°。结果如图13所示,实验结果表明动态实验结果和静态结果基本一致,测量精度随着距离的增加而变差。 (a)x轴方向动态测量位置误差 (b)y轴方向动态测量位置误差 (c)z轴方向动态测量位置误差 (d)绕x轴动态测量角度误差 (e)绕y轴动态测量角度误差 (f)绕z轴动态测量角度误差 本文针对一系列含有圆和直线特征的航天器,提出一种基于嵌入式实现的非合作视觉姿态测量系统。算法通过基于弧段的快速椭圆检测以及高精度二次Hough直线提取降低了内存空间的需求并且提高了计算速度,实现嵌入式。分两部分实验证明了该算法的有效性,椭圆检测实验证明了本算法在综合考虑检测精度和计算时间方面是最优的,姿态检测实验证明了本算法可嵌入式实现,并且具有良好的性能。近距离时小于4 m:深度方向平移误差优于100 mm,非深度方向平移误差优于60 mm,角度旋转测量误差优于1°。基本能够满足在轨任务的要求。 [1] JOEL A, STERGIOS I. A direct least-squares(dls) solution for PnP[C].ProceedingsoftheIEEEInternationalConferenceonComputerVision, 2011:383-390. [2] 赵汝进,张启衡, 左颢睿,等. 基于去离群点策略提高目标位姿测量精度[J]. 光学学报,2009,29(9):2463-2467 ZHAO R J, ZHANG Q H, ZUO H R,etal.. A method of improving the measuring accuracy of the pose of targets based on outliers-removal [J].ActaOpticaSinica, 2009,29(9): 2463-2467.(in Chinese) [3] VINCENT L, FRANCESC M N, PASCAL F. EPnP: an accurate non-iterativeO(n) solution to thePnPproblem [J].InternationalJ.ComputerVision, 2009, 81(2):155-166. [4] 崔乃刚,王平,郭继峰,等.空间在轨服务技术发展综述[J].宇航学报,2007,28(4):805-811. CUI N G, WANG P,GUO J F,etal.. A review of on-orbit servicing [J].JournalofAstronautics,2007,28(4):805-811.(in Chinese) [5] MIRAVET C, PASCUAL L, KROUCH E,etal.. An image-based sensor system for autonomous rendez-vous with uncooperative satellites [J].EprintArxiv, 2008. [6] TERUI F, KAMIMURA H, NISHIDA S. Motion estimation to a failed satellite on orbit using stereo vision and 3D model matching [C].9thInternationalConferenceonControl,Automation,RoboticsandVision, 2006,ICARCV′06, 2006:1-8. [7] CHIEN C H. Target acquisition using natural feature image recognition [C].AerospaceConference,IEEE,2009:1-7. [8] 徐文福,刘宇,梁斌,等.非合作航天器的相对位姿测量[J].光学 精密工程,2009,17(7): 1570-1581. XU W F, LIU Y, LIANG B,etal.. Mearsurement of relative poses between two non-cooperative spacecrafts [J].Opt,PrecisionEng., 2009, 17(7): 1570-1581.(in Chinese) [9] 苗锡奎,朱枫,丁庆海,等. 基于星箭对接环部件的飞行器单目视觉位姿测量方法[J].光学学报,2013,33(4):0412006. MIAO X K, ZHU F, DING Q H. Monocular vision pose measurement based on Docking ring component [J].ActaOpticaSinica, 2013, 33(4):0412006.(in Chinese) [10] CHAUDHURI D. A simple least squares method for fitting of ellipses and circles depends on border points of a two-tone image and their 3-D extensions [J].PatternRecognitionLetters, 2010, 31(9): 818-829. [11] FITZGIBBON A, PILU M, FISHER R B. Direct least square fitting of ellipses [J].IEEETransactionsonPatternAnalysisandMachineIntelligence, 1999, 21(5): 476-480. [12] CABRERA J, MEER P. Unbiased estimation of ellipses by bootstrapping [J].IEEETransactionsonPatternAnalysisandMachineIntelligence, 1996, 18(7): 752-756. [13] DUDA R O, HART P E.PatternClassificationandSceneAnalysis[M]. New York: Wiley Publishers, 1973. [14] CHIA A, LEUNG M, ENG H L,etal.. Ellipse detection with Hough transform in one dimensional parametric space [C].ProceedingsofIEEEInternationalConferenceonImageProcessing, 2007, 5: 333-336. [15] CHENG Z G, LIU Y C. Efficient technique for ellipse detection using restricted randomized Hough transform [C].ProceedingsoftheInternationalConferenceonInformationTechnology, 2004: 714-718. [16] MAI F, HUNG Y, ZHONG H,etal.. A hierarchical approach for fast and robust ellipse extraction [J].PatternRecognition, 2008, 41(8): 2512-2524. [17] CHIA A S, RAHARDJA S, RAJAN D,etal. A split and merge based ellipse detector with self-correcting capability [J].IEEETrans.ImageProcess, 2011, 20(7): 1991-2006. [18] PRASAD D K, LEUNG M K, CHO S Y. Edge curvature and convexity based ellipse detection method [J].PatternRecognition, 2012 45(9): 3204-3221. [19] LAM L, LEE S W. Thinning methodologies-a comprehensive survey [J].IEEETransactionsonPatternAnalysisandMachineIntelligence, 1992,14(9): 869-885. [20] SHIU Y C, AHMAD S. 3D location of circular and spherical features by monocular model-based vision [C].ProceedingsoftheIEEEInternationalConferenceonSystems,ManandCybernetics. 1989: 576-581. [21] MCLAUGHLIN R A. Randomized hough transform: improved ellipse detection with comparison [J].PatternRecognitionLetter, 1998, 19(3): 299-305. 吴 斌(1987-),男,江西南昌人,博士研究生,2011年于哈尔滨工业大学获得硕士学位,主要从事机器视觉的研究。E-mail: wubin5652005@163.com 导师简介: 叶 东(1968-),男,博士,教授,主要从事基于串/并联结构的坐标测量理论和技术、双目/单目视觉坐标测量理论和技术等方向的研究。E-mail:yedong@hit.edu.cn (版权所有 未经许可 不得转载) Embedded algorithm for relative pose measurement between non-cooperative targets WU Bin, YE Dong*, ZHANG Xin,ZHAO Zhen-qing (School of Electrical Engineering and Automation,HarbinInstituteofTechnology,Harbin150001,China) For the spacecrafts with circle and line features, an algorithm for embedded vision applications was proposed for the relative pose measurement between non-cooperative targets. The edge points were detected by a Canny edge detector and the image thinning was performed in a Field Programming Gate Array(FPGA). Then, elliptic characters on the target were detected by a novel ellipse detection algorithm based on edge contour in a Digital Signal Processor(DSP), and line features on the target were detected by a real-time and high accuracy method base on Hough Transform(HT). Finally, a ground simulation experiment was performed for a practical mission on orbit. and the relative attitude between target spacecraft and CCD camera was calculated by the obtained ellipse and lines. Experimental results show that the proposed method have been implemented in the embedded system and the update rate is more than 3 Hz. The measurement accuracy becomes poorer with the increasing of measuring distance and that in three directions is different even in the same measure distance. When the measuring distance is less than 4 m, the measurement accuracy in the depth direction is higher than 100 mm, other directions is higher than 60 mm and the angle accuracy is higher than 1°. The obtained results meet the requirement of the embedded system for the system resource, update rate and the detection accuracy. computer vision; non-cooperative target; pose measurement; ellipse detection; hough transform 2016-06-06; 2016-07-02. 国家自然科学基金资助项目(No.51075095) 1004-924X(2016)11-2804-10 V448.22 A 10.3788/OPE.20162411.2804 *Correspondingauthor,E-mail:yedong@hit.edu.cn
4 直线检测

5 姿态解算








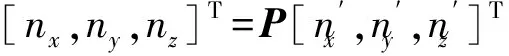
6 实验结果











7 结 论



