偏置磁场对磁致伸缩液位传感器检测电压的影响

孙 英， 边天元， 王 硕， 翁 玲， 张露予

(河北工业大学 电磁场与电器可靠性省部共建重点实验室， 天津 300130)



偏置磁场对磁致伸缩液位传感器检测电压的影响

孙 英*， 边天元， 王 硕， 翁 玲， 张露予

(河北工业大学 电磁场与电器可靠性省部共建重点实验室， 天津 300130)

为了提高磁致伸缩液位传感器的检测精度，研究了磁致伸缩液位传感器中产生偏置磁场的浮子磁铁的放置方式及其对检测电压的影响。利用ANSYS软件对浮子磁铁不同放置方式下形成的偏置磁场进行了有限元分析，分析显示：采用3块磁铁互成120°N极N极S极(NNS)放置或者采用圆环磁铁作为偏置磁场时检测效果比较理想。实验研究了磁致伸缩液位传感器的偏置磁场对检测电压的影响，并在浮子磁铁不同放置方式下进行多次实验。结果表明：偏置磁铁为3块磁铁互成120°NNS放置时或者为圆环磁铁时，检测电压的幅值达到50 mV，比其它放置方式提高了近30 mV。研究表明：磁致伸缩液位传感器应选择3块磁铁NNS放置或者选择圆环磁铁作为偏置磁场。

偏置磁场；磁致伸缩液位传感器；检测电压；有限元法

1 引 言

随着工业化进程的不断提高，液位测量的精度和对测量环境的工业性要求也越来越高，传统的液位传感器已不能满足工业要求。磁致伸缩液位传感器作为一种新型的传感器，具有测量精度高、测量位移大、测量非接触等优点，适用于恶劣环境中对液体位置的测量[1-8]。张露予等[9]构建了磁致伸缩位移传感器检测电压输出模型，搭建了实验平台；孙英等[10]研究了磁致伸缩液位传感器检测信号的影响因素，分析了激励电流和检测线圈对检测电压的影响；余超等[11]对磁致伸缩位移传感器的磁场进行了研究，分析了位移传感器的磁场分布；竺冉等[12]研究了磁致伸缩纵向导波传感器中偏置磁场的优化与设计。然而，对于磁致伸缩液位传感器中产生偏置磁场的浮子磁铁放置方式及其对检测电压的影响研究较少。而不同的磁铁放置方式导致产生的偏置磁场不同，进而影响检测电压。为此，本文从理论和实验两方面，对不同的磁铁放置方式，及其对检测电压的影响做了较详细地分析。

2 磁致伸缩液位传感器实验平台

实验测试平台如图1所示[9-10]。磁致伸缩液位传感器由传感器头部、检测线圈、波导丝、浮子等组成。将直径为0.5 mm，长度为1 m的磁致伸缩波导丝固定在内径为6 mm，外径为8 mm的铁氟龙塑料管内，底端穿过橡胶棒紧固，再套入内径为9 mm，外径为14 mm，壁厚为2.5 mm的316L不锈钢探杆内。检测线圈穿过波导丝，用于信号拾取，采用DPO3014示波器显示检测电压信号。检测线圈截面直径为1 mm，长度为8 mm，线圈匝数为800，使用的漆包线线径为0.06 mm[10，13]。其中传感器头部产生脉冲电流信号并处理后续检测电压信号；浮子中的磁铁为波导丝的磁致伸缩效应提供偏置磁场。在室温条件下，进行实验测试。

图1 搭建实验测试平台

3 磁致伸缩液位传感器信号产生原理

磁致伸缩液位传感器信号的产生源于磁致伸缩材料的魏德曼效应，信号产生过程如图2所示。

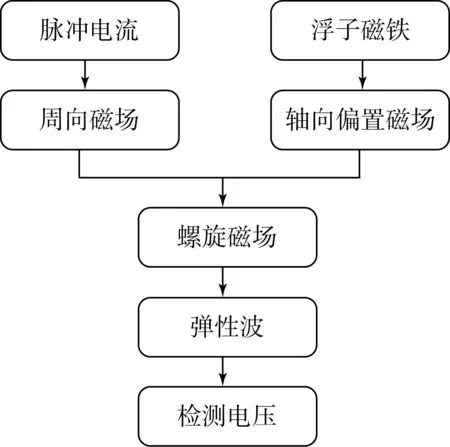
图2 信号产生流程图

在魏德曼效应的作用下，波导丝中的磁畴被轴向偏置磁场磁化，传感器头部的主控制器芯片发射起始脉冲信号，计时电路开始计时。脉冲沿着波导丝传播，并产生环绕波导丝的周向磁场，当波导丝中被偏置磁场磁化的磁畴受到周向磁场的作用时，磁畴发生局部偏转，质点偏离其平衡位置运动，由于质点间的相互作用，质点的振动由近及远地传播形成了弹性波[14-15]。当弹性波到达检测线圈时，在逆磁致伸缩效应的作用下，机械应力的改变导致波导丝中磁感应强度发生变化，因此在检测线圈两端便产生感应电压，即检测电压信号。检测电压信号经过比较、放大电路后作为计时电路的终止信号。

由电磁学理论可知，脉冲电流所产生的周向磁场是对称的同心圆，由于电流的集肤效应，磁感应强度随着波导丝半径的增大而增大，并在波导丝的最大半径处达到最大值。由于波导丝的磁导率比空气大得多，因此，脉冲电流所产生的周向磁场主要集中在波导丝内。轴向磁场是表征浮子中磁铁位移的量[9]，与波导丝上电流形成的周向磁场相遇后，矢量叠加形成螺旋磁场。为了检测电压幅值更大，要求螺旋磁场的磁场强度必须足够大，集中性好并且具有较好的峰值[16]。

其中，检测电压信号作为比较放大电路的输入，其波形决定着磁致伸缩液位传感器的检测精度。对于检测电压信号波形有两点要求。首先，在后续电路的处理过程中，需要在检测波形产生的时刻就终止计时，但是由于剩磁、回波等影响，使得检测电压信号波形在信号产生之前就存在起伏波动，所以后续电路必须设置阈值电压，避免计时电路误动作。为了减小磁致伸缩液位传感器的误差，要求检测电压波形，从信号产生到达到阈值电压的过程非常短，所以电压上升和电压下降的速度要求足够快。其次，为了方便，后续电路对检测电压信号进行半波整形，只保留正向电压。如果检测电压波形是中心对称图形，这样就存在先出现波峰时刻或是先出现波谷时刻两种情况。如果先出现波谷，由于进行了半波整形操作，使得计时延后半个信号宽度，反映在位移上，误差约为5.5 cm。在没有示波器的情况下无法判断先出现波峰或者波谷，为稳妥起见，波形尽量为轴对称图形。

由此可知，检测电压的波形不仅受材料特性的影响，同时还受激励磁场和偏置磁场的影响。浮子中磁铁的尺寸、放置方式等的不同，导致偏置磁场对磁致伸缩液位传感器检测信号影响的讨论比较困难。目前市场上流行的磁致伸缩液位传感器，浮子中磁铁的放置方式大体可以分为4类：第一类是单块磁铁，第二类是2块磁铁平行放置，第三类是3块磁铁互成120°，第四类是圆环磁铁。

4 磁致伸缩液位传感器偏置磁场理

论分析

ANSYS对磁场特性进行数值分析的方法有很多，其中有限元相关模型最为成熟，应用也最为广泛。首先对单块磁铁形成的偏置磁场进行分析，相关的参数设置如表1所示。

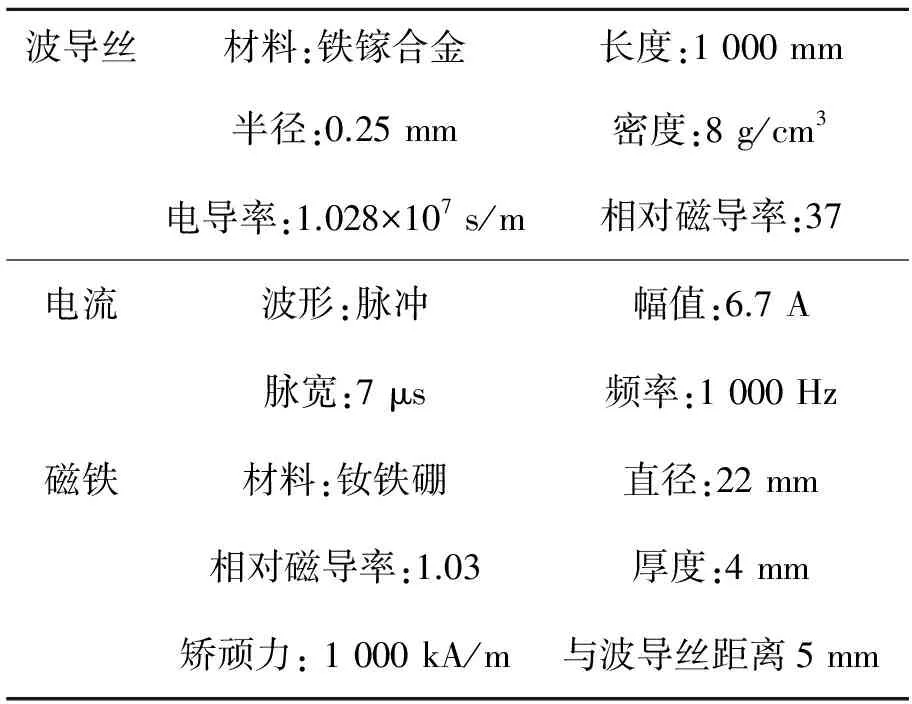
表1 实验及仿真参数

4.1 单块磁铁放置方式

波导丝与永久磁铁放置方式如图3所示，永久磁铁中心距波导丝5 mm。

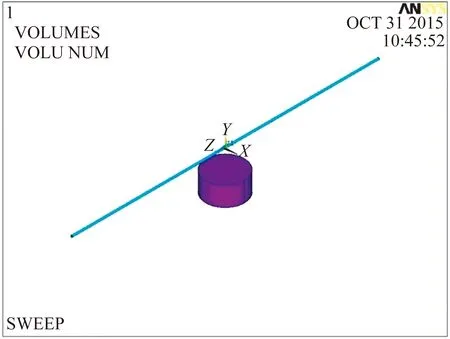
图3 单块磁铁放置方式

对磁铁模型进行有限元建模、仿真，波导丝内的磁场强度H的分布如图4所示。仿真时，波导丝内通入的电流大小为2 A，磁铁的矫顽力设置为1 000 kA/m。

图4 波导丝内部磁场强度分布图

由图4可以看出，波导丝内部磁场强度在磁铁处达到最大值。研究磁铁到波导丝的距离从1～30 mm，利用有限元软件的循环命令对波导丝的磁场强度进行分析，得到磁场强度随距离的变化，结果如图5所示。

图5 磁场强度随距离的变化

由图5可以看出，磁铁距离波导丝较近时，波导丝内部磁场强度较大，当磁铁与波导丝的距离达到20 mm以上时，磁铁对波导丝几乎没有影响。当磁铁距离波导丝较近时，在波导丝内部形成的磁场出现2个峰值，反映在检测电压波形上会出现双波峰，这不利于波导丝内弹性波的产生，并且会对磁致伸缩液位传感器的精度产生影响，因此单块磁铁放置方式存在缺陷。

4.2 2块磁铁平行放置方式

波导丝与2块磁铁的放置方式如图6所示，靠近波导丝的磁极为NN极。2块磁铁平行放置，波导丝垂直穿过2块磁铁中心的连线。靠近波导丝的磁极为NN极。每块永久磁铁中心距离波导丝5 mm，利用有限元软件的循环命令，改变磁铁与波导丝的距离，研究波导丝内部的磁场强度，结果如图7所示。磁铁与波导丝距离较近时，波导丝内部形成的磁场较大；磁铁与波导丝距离较远，超过20 mm时，波导丝内部的磁场几乎不受偏置磁场的影响。当二者距离较近时，在波导丝内部形成的磁场存在2个波峰，同样不利于弹性波的产生，影响磁致伸缩液位传感器的精度。

图6 2块磁铁平行放置方式

图7 磁场强度随距离的变化

4.3 3块磁铁互成120°的放置方式

互成120°的3块磁铁放置方式如图8所示，靠近波导丝的磁极为NNN极。

图8 3块磁铁互成120°放置方式

在相同参数下，研究磁铁到波导丝的距离从1～30 mm，利用有限元软件的循环命令对波导丝内部磁场进行分析，磁场强度随距离的变化结果如图9所示。

图9 磁场强度随距离的变化

同理，改变靠近波导丝的磁极为NNS，在相同的参数下，研究磁铁到波导丝的距离从1～30 mm，利用有限元软件的循环命令对波导丝内部磁场进行分析，磁场强度随距离的变化结果如图10所示。

图10 磁场强度随距离的变化

4.4 圆环磁铁放置方式

用同样的方法对圆环磁铁进行分析，其放置方式如图11所示。

图11 圆环磁铁放置方式

在相同的参数下，研究磁铁到波导丝的距离从1～30 mm，利用有限元软件的循环命令对波导丝的磁场强度进行分析，磁场强度随距离的变化结果如图12所示。

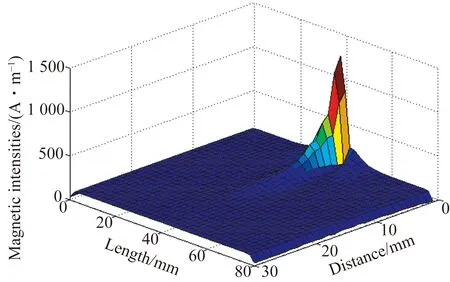
图12 磁场强度随距离的变化

综合比较图5、图7、图9、图10与图12可知，单块磁铁、2块磁铁与3块磁铁NNN放置在波导丝处均有2处峰值，而3块磁铁NNS放置与圆环磁铁在波导丝上的磁场只有1个峰值，除此之外，3块磁铁NNS放置与圆环磁铁在波导丝内部形成的磁场更为集中，同时单块磁铁、2块磁铁与3块磁铁NNN放置在波导丝内形成的磁场的磁场强度均未超过2 500 A·m-1，而3块磁铁NNS放置与圆环磁铁所形成磁场的磁场强度均超过10 000 A·m-1。综上所述，选择3块磁铁NNS放置或圆环磁铁作为磁致伸缩液位传感器的偏置磁场较为适宜。

5 磁致伸缩液位传感器实验结果与分析

4种磁铁的放置方式及规格如表2所示。实验中磁致伸缩液位传感器的其它参数如表1所示。

表2 磁铁放置方式及参数

5.1 单块磁铁的影响

浮子中的磁铁为单块磁铁时磁致伸缩液位传感器的检测电压如图12所示。为了后续电路检测的准确性，提高磁致伸缩液位传感器的精度，要求磁致伸缩液位传感器的检测信号波形呈轴对称图形，并且峰值单一，电压上升和下降的速度要足够快。由图12可知，此时磁致伸缩液位传感器的检测信号并非轴对称图形，且峰值的坡度不大。如果把此波形作为比较放大电路的输入波形，这在很大程度上影响了磁致伸缩液位传感器的精度。

图12 单块磁铁时的检测电压信号

5.2 2块磁铁的影响

在波导丝上下两端平行的2块磁铁，其放置方式不同，一种是靠近波导丝的磁极为NN，称为NN放置；另一种是靠近波导丝的磁极为NS，称为NS放置。

根据电磁学理论，当波导丝两端的磁铁NS放置时，形成的磁场在很大程度上与单块磁铁放置是一致的，所以其形成的检测电压波形大体形状相同。图13所示为2块磁铁NS相对平行放置时检测电压信号。由图13可知，此时检测电压的波形为中心对称图形，与图12所示单块磁铁放置时的检测电压波形大体相同。由于2块磁铁的存在，其磁场强度较单块磁铁的磁场强度大，所以其检测电压的幅值也较单块磁铁检测电压的幅值大。

图13 两块磁铁NS放置时的检测电压信号

Fig.13 Detection voltage signal with two pieces of parallel magnets under NS placement

图14所示为2块磁铁NN相对平行放置时，磁致伸缩液位传感器的检测电压信号。由图14可以看出，此时的检测电压存在2个波峰，并且检测电压幅值仅为16 mV，大大影响磁致伸缩液位传感器的精度，理论上应该舍弃这种设计方法。

图14 两块磁铁NN放置时的检测电压信号

Fig.14 Detection voltage signal with two pieces of parallel magnets under NN placement

5.3 3块磁铁互成120°的影响

3块磁铁互成120°时有2种放置方式，一种是靠近波导丝的磁极为NNN，称为NNN放置方式；一种是靠近波导丝的磁极为NNS，称为NNS放置方式。

在放置磁铁时，3块磁铁的重心所在的平面需与波导丝横截面平行，且两两重心所形成的夹角为120°。图15所示为NNN方式时，磁致伸缩液位传感器的检测电压信号。此时检测电压的波形为双波峰，确定其中心位置时存在难度，影响检测精度，理论上应予以舍弃。

图15 3块磁铁NNN放置时的检测电压信号

Fig.15 Detection voltage signal with three pieces of magnets under NNN placement

图16所示为NNS放置时的检测电压信号。由图16可知，此时的波形基本呈轴对称分布，且波峰波谷的坡度较好，可以作为比较放大电路的输入。

图16 三块NNS放置时的检测电压信号

Fig.16 Detection voltage signal with three pieces of magnets under NNS placement

5.4 圆环磁铁的影响

放置圆环磁铁时尽量使得波导丝垂直穿过圆环磁铁，并处于圆环磁铁的中心。图17所示为圆环磁铁对磁致伸缩液位传感器检测电压信号。由图17可知，此时波形呈标准的轴对称图形，且波峰具有非常好的坡度，波谷幅值是波峰幅值的1/3。

图17 圆环磁铁时的检测电压信号

综合比较图12～17，单块磁铁放置与2块磁铁NS放置时，其波形大体一致，均为中心对称图形。两块磁铁NN放置与3块磁铁NNN放置时，其波形大体相同，都同时存在2个波峰和1个波谷，而且这两种放置方式下，检测电压的幅值非常低，仅为16 mV和13 mV，大大影响了磁致伸缩液位传感器的精度；3块磁铁NNS放置与圆环磁铁放置时，检测电压波形为中心对称图形，而且幅值也非常理想，是同种测试条件下NN放置与NNN放置的3～4倍，为了使检测电压波形更为标准，检测精度更高，后续电路的处理更为便捷，可以选择3块磁铁NNS放置或者圆环磁铁作为偏置磁场。

6 结 论

单块磁铁和两块磁铁NS平行放置对检测信号的影响大体相同，由于检测信号呈中心对称，应该予以舍弃。2块磁铁NN放置和3块磁铁NNN放置对检测信号的影响大体相同，此时存在2个波峰和1个波谷，无法确定中心位置，应该予以舍弃。3块磁铁NNS放置和圆环磁铁对检测信号的影响大体相同，波形都呈轴对称分布，并且都有很好的坡度。此时的检测电压幅值为50 mV，远远超过其它几种放置方式，可以选择3块磁铁NNS放置或者圆环磁铁作为偏置磁场。利用ANSYS软件对浮子中磁铁不同放置方式下形成的偏置磁场进行了有限元分析，并且实验测试分析了该偏置磁场对检测电压的影响，研究结果为磁致伸缩液位传感器的设计提供了依据。

[1] 王博文，张露予，王鹏，等. 磁致伸缩位移传感器检测信号分析[J].光学 精密工程， 2016， 14(2)：358-364. WANG B W， ZHANG L Y， WANG P，etal.. Analysis of detection signal for magnetostrictive displacement sensor [J].Opt.PrecisionEng.， 2016， 14(2)：358-364.(in Chinese)

[2] 程鹏，高爽，张文栋，等. 基于阻抗响应的磁弹性传感器共振频率测量系统[J]. 光学 精密工程， 2014，22(11)：3012-3018. CHENG P， GAO SH， ZHANG W D，etal.. Resonant frequency measurement system for magnetoelastic sensor based on impedance response [J].Opt.PrecisionEng.， 2014，22(11)：3012-3018.(in Chinese)

[3] FEMANDO S， JOSE M M， ANTONIO R J. Improving the accuracy of magnetostrictive linear position sensors [J].IEEETransactionsonInstrumentationandMeasurement， 2009， 3(58)： 722-728.

[4] 姜建山，陈伟民. 外力对逆磁致伸缩索力传感器影响研究[J]. 传感技术学报， 2009， 3(22)：439-441. JIANG J SH， CHEN W M. Study on cable tension stress influence of cable tension sensor based on Villari-Effect [J].ChineseJournalofSensorandActuators， 2009， 3(22)： 439-441.(in Chinese)

[5] 薛光明，张培林，何忠波，等. 强偏置超磁致伸缩致动器准静态位移建模与试验[J]. 农业机械学报， 2015，46(7)： 318-324. XUE G M， ZHANG P L， HE ZH B，etal.. Modelling and experiment of strong bias giant magnetostrictive actuator’s semi-static displacement [J].TransactionsoftheChineseSocietyforAgriculturalMachinery， 2015， 46(7)： 318-324.(in Chinese)

[6] 毛君，谢春雪，孟洋，等. 磁致伸缩液位传感器温度补偿方法研究[J]. 控制工程， 2015，22(5)：921-926. MAO J， XIE CH X， MENG Y，etal.. Study on magnetostrictive liquid level sensor temperature compensation method [J].ControlEngineeringofChina， 2015， 22(5)： 921-926.(in Chinese)

[7] 杨星红，黄皎，陆晓春，等. 智能磁致伸缩液位测量仪设计[J]. 传感器与微系统， 2016，35(3)： 118-123. YANG X H，HUANG J，LU X CH，etal.. Design of intelligent magnetostrictive liquid level gauge [J].TransducerandMicrosystemTechnologies， 2016， 35(3)： 118-123.(in Chinese)

[8] 刘孝亮，邬义杰，章一智，等. 超磁致伸缩执行器率相关迟滞混合模型研究[J]. 农业机械学报， 2014，45(7)： 286-291. LIU X L， WU Y J， ZHANG Y ZH，etal.. Hybrid rate-dependent hysteresis model in giant magnetostrictive actuaor [J].TransactionsoftheChineseSocietyforAgriculturalMachinery， 2014， 45(7)： 286-291.(in Chinese)

[9] 张露予，王博文，翁玲，等. 螺旋磁场作用下磁致伸缩位移传感器的输出电压模型及实验[J]. 电工技术学报， 2015， 30(12)： 21～26. ZHANG L Y， WANG B W， WENG L，etal.. The output voltage model of magnetostrictive displacement sensor in helical magnetic fields and its experimental study [J].TransactionsofChinaElectrotechnicalSociety， 2015， 30(12)： 21-26.(in Chinese)

[10] 孙英，靳辉，郑奕，等. 磁致伸缩液位传感器检测信号影响因素分析及实验研[J]. 传感技术学报， 2015，28(11)： 1607-1613. SUN Y， JIN H， ZHENG Y，etal.. Detective signal influence factor analysis and experimental research of magnetostrictive liquid level sensor [J].ChineseJournalofSensorandActuators， 2015， 28(11)： 1607-1613.(in Chinese)

[11] 余超，周新志. Fe83Ga17磁致伸缩位移传感器激励信号的ANSYS分析及DSP实现[J]. 仪表技术与传感器， 2012(8)： 4-6. YU CH， ZHOU X ZH. Research on excitation signal of Fe83Ga17magnetostrictive displacement sensor based on ANSYS and DSP [J].InstrumentTechniqueandSensor， 2012(8)： 4-6.(in Chinese)

[12] 竺冉，吕福在，唐志峰，等. 磁致伸缩纵向导波传感器中偏置磁场的优化设计[J]. 传感技术学报， 2011， 24(3)： 371-375. ZHU R， LV F Z， TANG ZH F，etal.. Bias bagnetic field optimization of longitudinal modes guided wave sensor based on magnetostriction [J].ChineseJournalofSensorandActuators， 2011， 24(3)： 371-375.(in Chinese)

[13] 张岚， 卜雄洙， 赵文. 磁致位移传感器检测线圈和驱动脉冲优化设计[J]. 自动化仪表， 2011，32(5)： 59-62. ZHANG L， BU X ZH， ZHAO W. Optimal design of detecting coil and energizing pulse in magnetostrictive displacement sensor [J].ProcessAutomationInstrumentation， 2011， 32(5)： 59-62.(in Chinese)

[14] 王铮， 常晓明， 脇若弘之. 长线磁致伸缩位移传感器激励波的研究[J]. 太原理工大学学报， 2010，41(3)： 241-244. WANG ZH， CHANG X M， HIROYUKI W. Study on impulse wave of magnetostrictive position line sensor [J].JournalofTaiyuanUniversityofTechnology， 2010， 41(3)： 241-244.(in Chinese)

[15] 王铮， 常晓明， 脇若弘之. 长线磁致伸缩位移传感器的磁极化强度模型[J]. 传感技术学报， 2010，23(8)： 1075-1078. WANG ZH， CHANG X M， HIROYUKI W. Magnetic pole intensity model of magnetostrictive position sensor [J].ChineseJournalofSensorandActuators， 2010， 23(8)： 1075-1078.(in Chinese)

[16] 代前国，周新志. 大位移磁致伸缩传感器的弹性波建模与分析[J]. 传感技术学报， 2013，26(2)： 195-199. DAI Q G，ZHOU X ZH. Modeling and analysis of elastic wave of large-range magnetostrictive displacement sensor [J].ChineseJournalofSensorandActuators， 2013， 26(2)： 195-199.(in Chinese)

孙 英(1970-)，女，河北唐山人，博士，副教授，硕士生导师，1994年、2001年、2008年于河北工学院分别获得学士、硕士、博士学位，主要从事磁器件设计、建模及控制等研究。E-mail：sunying@hebut.edu.cn

边天元(1990-)，男，河北唐山人，硕士研究生，2014年于太原科技大学获得学士学位，主要从事磁器件设计及其检测技术等研究。E-mail：1125339175@qq.com

(版权所有 未经许可 不得转载)

Influence of bias magnetic field on detection voltage of magnetostrictive liquid level sensor

SUN Ying*， BIAN Tian-yuan， WANG Shuo， WENG Ling， ZHANG Lu-yu

(Province-Ministry Joint Key Laboratory of Electromagnetic Field and ElectricalApparatusReliability，HebeiUniversityofTechnology，Tianjin300130，China)

To improve the detection accuracy of a magnetostrictive liquid level sensor， different placements of float magnets in the bias magnetic fields of the sensor and its impact on the detection voltage were researched. The bias magnetic fields generated by float magnets in different placements were analyzed by the finite element analysis of ANSYS software. It was found that when three pieces of magnets under NNS placement or one single ring magnet are chosen as bias magnetic field， the detection voltage waveform is in line with expectations. Besides， the effects of bias magnetic field of magnetostrictive liquid level sensor were done on detection voltage were experimentally studied and the experiments were done more times for the float magnets at different placements. The experiment results verify that when the bias magnetic field is generated by three pieces of magnets under NNS placement or one single ring magnet， the amplitude of detection voltage reaches 50 mV， which has improved almost 30 mV as compared with that of other ways. It suggests that three pieces of magnets under NNS placement or one single ring magnet can be applied as the bias magnetic field of magnetostrictive liquid level sensors.

bias magnetic field； magnetostrictive liquid level sensor； detection voltage； finite element method

2016-05-20；

2016-07-10.

国家自然科学基金资助项目(No.51201055);河北省高等学校科学技术研究重点资助项目(No.ZD2015085);天津市高等学校科技发展基金资助项目(No.20140421)；河北省引进留学人员资助项目(No.CG2013003001)

1004-924X(2016)11-2783-09

TP212.12

A

10.3788/OPE.20162411.2783

*Correspondingauthor，E-mail：sunying@hebut.edu.cn