卸荷诱发巷道模型岩爆的发生机理实验研究*

刘祥鑫 梁正召 张艳博 姚旭龙 李海洋

LIU Xiangxin① LIANG Zhengzhao② ZHANG Yanbo① YAO Xulong① LI Haiyang①



卸荷诱发巷道模型岩爆的发生机理实验研究*

刘祥鑫①梁正召②张艳博①姚旭龙①李海洋①

以“巷道-围岩”系统为研究对象，以水平应力卸荷操作模拟工程现场的巷道周边矿岩开挖卸荷作用，再现了巷道卸荷岩爆。实验结果指出，巷道卸荷岩爆经历了“平静期→小颗粒弹射→片状剥离→片状剥落”的演化过程，在巷道内壁产生“岩爆→应力调整→应力调整失败→再次岩爆”的多次岩爆过程，最终形成“V”字型岩爆坑。卸荷条件下，不同水平应力的巷道模型岩爆将产生不同的破坏，形成了不同的破裂面。理论推导得出卸荷前巷道围岩的应力分布规律，运用修正Griffith破坏准则，计算了不同水平应力(8.9MPa、13.3MPa、17.8MPa)卸荷后巷道围岩发生岩爆破坏的竖向起裂应力，构建了巷道边壁“V”字型岩爆坑的计算模型。研究得出水平应力存在一个影响竖向承载能力的应力点(13.3MPa)，当水平应力小于13.3MPa时，水平应力与竖向起裂应力呈正相关； 当水平应力大于13.3MPa时，水平应力与竖向起裂应力呈负相关。对左右边壁应变能累积区域的信息进行量化处理，得出相较8.9MPa和17.8MPa，水平应力为13.3MPa的左右边帮应变能集中区域的累积能量最大，集中区域与边壁的距离最短。

岩石力学 卸荷 巷道模型 岩爆

LIU Xiangxin①LIANG Zhengzhao②ZHANG Yanbo①YAO Xulong①LI Haiyang①

0 引 言

在坚硬、脆性岩体的地下巷道中，对巷道周边岩体进行开挖操作，将对巷道产生卸荷扰动，导致围岩应力重分布，继而出现应力集中。若岩体内储存的弹性应变能突发性的急剧释放，产生爆裂松脱、岩屑剥落、岩块弹射等动力学现象，称之为岩爆(中国科协学会学术部， 2011)。任何破坏的发生都有一个从量变到质变的过程，岩爆的发生亦如此。由于现场岩体的非均质性、各向异性、不可视性，以及岩爆问题的复杂性、发生的瞬时性、不可逆性，监测结果的失真或误判时有发生。

在岩爆机理研究方面，基于非线性理论的混沌理论(谭云亮等， 2002)、突变理论(唐春安， 2002)、损伤理论(刘小明等， 1997)、分形理论(谢和平等， 1993)在岩爆问题中得到了广泛的应用。岩爆是突然的岩石破坏，是岩石的破碎和从围岩中突出并伴随着能量的猛烈释放(Brady et al.， 1990)。在地下硐室开挖中，高地应力环境下高储能脆性岩石通常会通过脆性破裂快速释放应变能，产生岩爆。即岩爆是伴随弹性能猛烈释放的岩体结构剧烈破坏现象，一般发生在较为完整的十分干燥的脆硬性岩石中。因此，硬岩岩爆的关键在于脆性破坏(陈宗基， 1987； 唐春安等， 1993； 伍法权等， 2010)。关于岩爆发生的本质问题，有学者指出就是围岩得到了高于破坏的能量，使碎屑获得了动能。如果没有多余的能量，就是普通的岩石破坏而不是岩爆。而从防治角度出发，岩爆也可定义为高地应力地区由于地下工程开挖卸荷引起的围岩弹射性破裂的现象(Linkov， 1996； 何满潮等， 2007； 钱七虎， 2014)。岩爆的孕育是从岩体破裂开始，并提出了预测和调控方案(冯夏庭等， 2012)。针对隧洞围岩工程地质分类问题，有学者将云模型理论应用于此，建立了隧洞分类多级定量指标体系及评价等级标准，判定隧洞围岩工程地质类别。针对一些地质条件复杂、巷道围岩较硬脆等情况，应用属性识别模型，建立了岩爆发生预测和烈度分级的属性识别模型，并且评判结果与人工神经网络法、距离判别法等的评判结果一致(文畅平， 2008； 张勇等， 2016)。岩体破裂过程的演变规律与能量及断裂的关系，学者总结出了固体强度的动能概念及刚度不连续下的开采微震事件的岩爆预测方法(Mamsurov， 2001)。在室内实验方面，通过开展含洞室岩体的双轴压缩状态的岩爆实验，采用模糊数学方法，总结出考虑多因素的岩爆预测方法。还有学者通过室内实验以及数值模拟研究构造应力对花岗岩巷道岩爆的影响，从可见光图像、声发射、远红外的变化规律入手，分析三者与巷道岩爆的内在联系，揭示巷道岩爆的孕育机制(秦乃兵， 2001； 张艳博等， 2014)。

本文通过双轴加载模拟地下巷道的应力环境，以水平卸荷操作模拟巷道周围岩体的开挖工序，分析水平卸荷后巷道围岩的应力演化特征，得到岩爆在巷道围岩的显现规律。理论求解不同水平应力的巷道围岩发生岩爆的竖向起裂应力值，得出巷道边壁的“V”字型岩爆坑的形成机理。采用Plaxis 3D数值模拟软件，模拟了水平卸荷作用下“巷道-围岩”系统的力学及能量分布规律，提取应力、应变及应变能集中区域的信息，并对水平应力与集中区域的相关信息展开讨论。最后，综合室内试验、理论推导、数值模拟3种手段，对卸荷诱发巷道模型岩爆的发生机理开展全方位讨论。

1 室内巷道模型卸荷岩爆试验

1.1 试样设计

将花岗岩制成150mm×150mm×150mm尺寸的岩样，通过磨石机磨平岩样6个端面，经过人工打磨，试样两端面高度差不大于0.05mm，端面不平整度误差不大于0.02mm，正中心钻直径为45mm通孔。

1.2 试验系统

巷道岩爆实验系统主要由加载系统、观测系统两部分组成，试验系统(图1)。

图1 试验系统

加载系统：RLW-3000双轴伺服岩石力学试验系统，该加载系统可对水平以及竖直进行独立控制。其中竖向最大试验力3000kN，横向最大试验力1000kN，试验力测量精度±1%。

观测系统：CCD高速相机、高清视频监控系统、数字摄像机3部分组成，构成立体观测系统。

1.3 试验过程

(1)水平方向首先以600N·s-1速率加载到预定值8.9MPa、13.3MPa、17.8MPa，轴向以1000N·s-1速率加载至花岗岩单轴抗压强度值的90%(97.8MPa)；

(2)保持当前应力环境5min；

(3)竖向保持不变，水平方向快速卸载(卸载速率为20mm·min-1)。

(4)若没有发生岩爆，水平方向恢复至最初状态，竖向增加50kN，重复步骤(3)，直到发生岩爆(图2)。

图2 水平方向卸荷前后岩石破裂形态

1.4 巷道卸荷岩爆特征

1.4.1 岩爆过程分析

何满潮等(2007)研究指出，典型的巷道岩爆可划分为：(1)平静期； (2)小颗粒弹射； (3)片状剥离伴； (4)岩爆发生。由试验观察得出，水平方向卸荷后，巷道内部也经历了4个过程 (图3)。

图3 岩爆孕育、发生过程

图4 “V”字型岩爆坑

在地下工程中，已成型的巷道由于周边岩体的开挖操作，形成卸荷力学效应，造成局部应力集中，产生松弛效应，差异回弹形成残余应力，形成卸荷岩体(费文平等， 2010)。岩体在卸荷条件下容易产生张开型裂隙，形成劈裂破坏，岩体积蓄的能量因为自由面的存在而更容易产生耗散，有利于岩体进一步发生张性破裂。

图5 岩爆后巷道模型破坏情况

图6 水平应力与声发射RA-AF值分布云图

1.4.2 “V”字型岩爆坑形成

在经历了图3 的4个阶段后，若巷道模型应力调整失败，且应变能还未完全耗散，孔洞内会再次出现图3d阶段，碎屑持续在内壁左右两侧剥落，并以一定速度弹射而出。围岩将经历“岩爆→应力调整→调整失败→再次岩爆”的循环过程，多次应力调整将形成多次岩爆。当聚集的能量耗散完后，岩爆停止，最终形成了图4 所示的“V”字型岩爆坑。

1.4.3 岩爆后的巷道模型整体破坏形态分析

岩爆是巷道模型内壁的局部应力集中所发生的急剧破坏现象，岩爆的发生也将造成巷道模型整体失稳破坏。8.9MPa， 13.3MPa， 17.8MPa属于水平应力，水平应力卸载诱发巷道模型内壁均发生岩爆。但岩爆后导致巷道整体所产生的破裂形态与剧烈程度与中间主应力不同。

破裂剧烈程度方面，水平应力13.3MPa破坏程度最严重，巷道模型变形最大(图5b内巷道模型)，且碎屑最为粉碎； 水平应力为17.8MPa发生岩爆时也产生了较大的破裂，相较于13.3MPa，碎屑尺寸较大； 水平应力为8.9MPa也形成了明显的破裂面，巷道模型变形最小。

破裂形态方面。水平应力为13.3MPa时，剪切破坏最明显，剪切裂纹最为发育 (图6b)，由于剪切应力超过了岩石材料晶体间的滑移、错位能力，使材料发生了剪切滑移破坏，造成13.3MPa出现了如图5b的整体粉碎情况； 水平应力为17.8MPa时(图5c)，形成了平行于最大主应力方向(竖向)的张拉破裂面，张性裂纹最为发育 (图6c)； 水平应力为8.9MPa时)(图5a)，由于水平应力最小，岩爆后发生的破坏最弱，形成破裂面的开合程度最小，破裂程度也最弱。

2 巷道模型卸荷岩爆的力学分析

2.1 巷道模型围岩应力分析

在实际矿山现场，巷道围岩处于三向应力状态，但沿巷道走向的受力及变形一般情况下可不予考虑。为简化计算，假设巷道产生的变形由横向以及竖向应力共同作用形成，可简化为平面应变问题(王嘉新， 1993)(图7)。以圆形巷道为例，围岩中的各向应力表示如下：

(1)

式中，p为竖向应力； q为横向应力； a为巷道半径； σr为径向应力；σθ为环向应力； τrθ为剪切应力； r为A点距巷道中心距离； μ为泊松比。

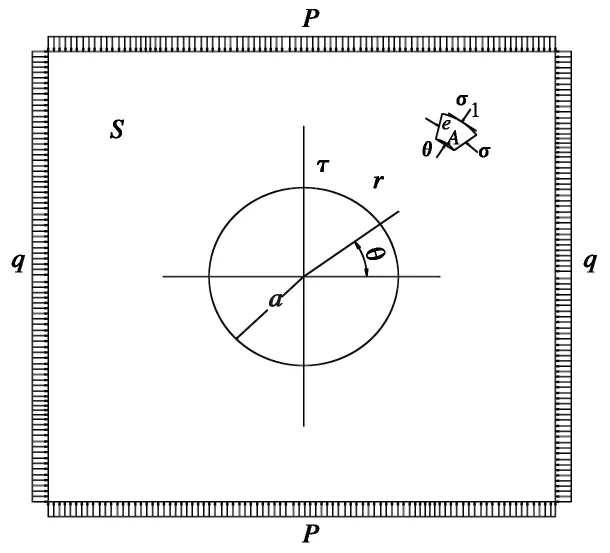
图7 巷道简化模型

在本次试验中，巷道围岩发生岩爆的位置位于巷道两侧，即左侧θ=180°，右侧θ=0°处，带入式(1)，可得：

(2)

在巷道左右壁面处，r=a，可得：

(3)

当竖向应力维持在97.8MPa(2200kN)，水平应力维持在8.9MPa或13.3MPa或17.8MPa时，巷道模型保持平衡。当水平应力卸荷，即巷道在水平方向卸荷时，式(3)中的q值迅速降低至0，造成σθ达到最大值3p，巷道左右边帮处发生岩爆破坏。

硬脆性围岩在洞壁平行于最大初始应力σ1，致使左右洞壁压致张裂，形成板状劈裂，产生如图3 的劈裂面。在此阶段，劈裂破坏经历了两个过程(图8)：(1)裂纹稳定扩展阶段，此阶段发生在竖向应力呈线性增加阶段，进入竖向应力和水平应力保载阶段时，裂纹扩展停止； (2)裂纹失稳扩展阶段，当水平发生卸荷作用时，裂纹失稳扩展，形成板状劈裂，此阶段为岩爆初级破坏阶段(谭以安， 1989)。

图8 巷道左右壁面处卸荷劈裂机制(王明洋等， 2010)

2.2 “V”字型岩爆坑力学模型构建及分析

巷道左右壁面处卸荷所产生的劈裂破坏，是巷道卸荷单次岩爆的形成机制。观察巷道模型演化过程，巷道围岩经历了多次颗粒弹射及片状剥落过程，即经历“岩爆→应力调整→调整失败→再次岩爆”的循环过程，最终在左右边壁形成“V”型岩爆坑。

卸荷操作后，巷道左右边壁的“V”型岩块受力情况(图9)，水平应力σh急剧下降至零，图中左边表示“V”型岩块所受竖向应力σa，右边表示将竖向应力σa分解成垂直于“V”型岩块斜面的正应力分量σP和平行于“V”型岩块斜面的切应力分量τ。

图9 “V”字型岩爆坑受力分析

其中求解σP和τ如下所示：

(4)

对“V”字型岩块进行受力分析可知，“V”字型岩爆坑的形成可分解为如下两个步骤：

第1，正应力分量σP形成向巷道面的破裂分量，即推动岩块向自由面运动的分量，从围岩中抛掷出去。可采用库仑抗剪强度准则进行求解。

即

(5)

第2，切应力分量τ将围岩剪切，最终形成OAB面积的“V”字型岩爆体。

水平应力的卸荷，造成竖向应力σa逐步递增，由于破裂的产生，岩石材料产生损伤，使其力学性质降低，导致岩石材料的c和φ数值降低。“V”字型岩爆坑的形成愈加迅速，在巷道模型纵向的左右边壁形成了如图10 所示的连续岩爆坑。

图10 孔洞内壁岩屑剥落情况

2.3 巷道模型卸荷后围岩应力集中分析

水平应力卸荷后，巷道模型围岩的左右两边帮出现应力集中，从而在此部位出现岩爆。若能掌握卸荷前后应力集中的规律，这必然能指导现场岩爆预防及治理工作。计算机数值模拟作为第3种研究方法，在岩石力学问题中得到了较为广泛的应用。

假设巷道围岩的微结构面相对于模拟尺寸为无穷小，且没有明显的层理结构，可将围岩材料看作均质、连续介质。采用基于有限元的Plaxis 3D三维数值模拟软件，开展水平应力卸荷作用下巷道模型的稳定性模拟工作，构建图11 所示的巷道模型，材料力学参数如表1所示。

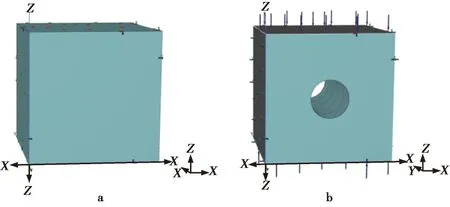
图11 实验模型

表1 材料力学参数

Table1 Mechanical parameters employed in simulation

参数名称重度/kN·mm-3弹性模量/kN·mm-2泊松比黏聚力/kN·mm-2内摩擦角/(°)围岩2.6360.000.25060

数值模拟的实验过程跟室内实验完全一致，具体模拟步骤如下：

第1阶段，导入试件模型，如图9a；

第2阶段，巷道模型形成，并对竖向及水平向加载至应力环境，如图9b；

第3阶段，保持应力环境50步(5min)；

第4阶段，以20mm·min-1速率水平卸荷，当水平应力降为0时，卸荷结束；

第5阶段，若巷道边壁并未发生岩爆，水平方向应力恢复至原始状态，竖向增加50kN，重复第4阶段，直到岩爆发生。

限于篇幅，针对巷道模型卸荷后围岩应力分析以水平应力8.9MPa为例。经“第1阶段→第2阶段→第3阶段→第4阶段”后，巷道围岩整体应力分布如图12 所示。

图12 巷道模型力学分布云图

如图12a所示，在巷道左右边壁出现了拉应力集中区C，在上下边壁出现压应力集中区P。左右边壁拉应力集中区C的最大拉应力数值为520kN·m-1m2， 上下边壁压应力集中区P的最大压应力数值为40kN·m-1m2。C区域面积也要小于P区域面积，即C区域集中度也要大于P区域，再结合岩石的拉应力是压应力的1/10～1/30，造成C区域比P区域更易出现破裂。

如图12b所示，在巷道左右边壁出现正应变E区域，表现为伸长类的膨胀效应。在巷道4个角出现负应变S区域，表现为压缩类收缩变形。其中左右边壁的正应变E区域的最大拉应变数值达3.5～4，而巷道4个角的S区域最大压缩应变为2，最大拉应变数>最大压缩应变。再结合拉应变将产生膨胀效应，而压缩应变对应收缩效应，E区域比S区域更易出现破裂。

综合巷道模型边壁的应力及应变分布可知，在左右边壁区域将出现拉应力C和拉应变集中E区域。因此，在巷道的左右边壁将出现拉破坏效果，率先出现岩爆。

3 讨 论

3.1 水平应力与巷道岩爆发生起裂应力关系

根据2.1关于巷道围岩的应力分析可知，在卸载瞬间，巷道左右壁面处的环向应力达到最大，此处的张性裂纹开始失稳扩展，该处围岩发生了劈裂破坏，即为岩爆显现初始阶段发生的具体位置。

在本实验中，水平应力卸荷试验形成岩爆是以劈裂显现的，是巷道围岩在双向受静水压后水平方向应力(小主应力)卸荷致拉的结果。Griffith准则是劈裂破坏的起裂准则，Murrell推广到二、三维应力空间的修正Griffith准则可表示如下：

(6)

式中，σ1为最大主应力； σ2和σ3为中间及最小主应力； σt为岩石抗拉强度。

图14 不同水平应力下巷道左右边帮能量集中情况

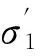
图13 竖向起裂应力与水平应力关系图

表2 岩爆发生的最大主应力对比

Table2 The maximum principal stress of rock burst occurrence

水平应力σ2/MPa式(6)计算最大竖向应力σ1/MPa实验测得最大竖向应力σ'1/MPa8.983.28013.394.9106.717.888.9100

(1)当水平应力σ2小于13.3MPa时，随着水平应力σ2的增加，竖向起裂应力也随之提升。

(2)当水平应力σ2大于13.3MPa时，随着水平应力σ2的增加，竖向起裂应力反而降低。

3.2 水平应力与巷道围岩张性应变集中区域关系

岩爆发生与能量的累积量、集中度以及释放速率有密切关系，竖向起裂应力的大小与应变能量累积量相关(兰天伟等， 2012)。水平应力为13.3MPa时，竖向起裂应力最大，这必然跟应变能的集中区域有直接关系。从图11 巷道模型力学分布云图可以发现，张性应变能主要集中区域分布在左右边壁(图14)。

如图14 所示，水平应力的不同，巷道左右边帮集中区域的信息也存在区别。根据圆形巷道受力的对称性，以左边帮的集中区域为例，求取区域的参量(表3)。其中集中区域面积与水平应力呈正相关； 区域平均有效应力则相差不大； 区域平均应变、区域能量以及区域距边壁距离则出现了图12 的规律，即水平应力为13.3MPa时，区域平均应变和区域距边壁距离出现了最低值，而区域能量却最大。

表3 左边帮集中区域信息统计表

Table3 Statistical table of concentrated area information on left side

水平应力/MPa区域面积/mm2区域平均有效应力/MPa区域平均应变区域能量/E3*J区域距边壁距离/mm8.920.72-290-1.64649.82513.357.57-300-2.26607.37117.8302.40-300-1.648011.886

图15为不同水平应力下左边帮集中区域应变能以及集中区域距边壁距离统计图形，结合图13 分析可知，在13.3MPa中，岩爆发生时的竖向应力起裂应力最大。这势必造成累积的应变能最多，同时结合集中区域与边壁的距离最小，水平应力13.3MPa发生的岩爆裂度最大。

图15 左边帮集中区域应变能以及距边壁距离统计图

4 结 论

(1)巷道卸荷岩爆经历了“平静期→小颗粒弹射→片状剥离伴→岩爆发生”的演化过程，在巷道内壁产生了“岩爆→应力调整→应力调整失败→再次岩爆”多次岩爆循环过程，最终形成“V”字型岩爆坑。在水平快速卸荷作用下，巷道围岩左右边壁形成一系列平行于洞壁连通性较差的张裂隙，这些张裂隙将洞壁围岩分割成颗粒状、板片状等小块状岩屑，岩屑向自由面弹射而出。

(2)水平应力为13.3MPa岩爆发生后，形成了明显的剪切滑移破坏。水平应力为17.8MPa卸荷后，巷道模型岩爆后将发生明显的张性破坏，形成平行于最大主应力的张性破裂面。水平应力为8.9MPa岩爆发生后，破裂尺度及破裂裂度最弱。

(3)对水平方向进行卸荷，巷道左右壁面产生平行于卸荷方向的拉应力，拉应力在水平应力卸为零时达到最大。运用修正Griffith破坏准则，计算了不同水平应力(8.9MPa、13.3MPa、17.8MPa)下巷道围岩发生岩爆破坏的竖向起裂应力值。

(4)水平应力存在一个影响岩爆起裂的竖向应力点(本研究为13.3MPa)。当水平应力小于13.3MPa，随水平应力的增加，竖向承载应力随之提升。当水平应力大于13.3MPa时，水平应力增加，竖向承载应力反而降低。

(5)水平应力为13.3MPa时，岩爆发生的裂度大于8.9MPa和17.8MPa。原因在于左右边帮的应变能集中区域的累积量最大，以及集中区域与边壁的距离最短。

Brady B H G，Brown E T.199. Underground mining rock mechanics[M]. Beijing： China Coal Industry Publishing House．

Fei W P，Zhang G Q，Cui H L. 2010. Stability analysis of unloading rockmass of high slopes[J]. Engineering Journal of Wuhan University，43(5)： 599～612．

Feng X T，Chen B R，Ming H J，et al. 2012. Evolution law and mechanism of rockbursts in deep tunnels： immediate rockburst[J]. Chinese Journal of Rock Mechanics and Engineering，31(3)： 433～444．

He M C，Miao J L，Li D J，et al. 2007. Experimental study on rockburst processes of granite specimen at great depth[J]. Chinese Journal of Rock Mechanics and Engineering，26(5)： 865～876．

Lan T W，Zhang H W，Han J，et al. 2012. Study on rock burst mechanism based on geo-stress and energy principle[J]. Journal of Mining & Safety Engineering， 29(6)： 840～844，875．

Linkov A M. 1996. Rockburst and the instability of rock masses[J]. International Journal of Rock Mechanics and Mining Sciences，33(1)： 727～732．

Liu X M. 1997. Damage mechanics analysis for brittle rock and rockburst energy index[J]. Chinese Journal of Rock Mechanics and Engineering，16(2)： 140～147．

Qian Q H. 2014. Definition， mechanism， classification and quantitative forecast model for rockburst and pressure bump[J]. Rock and Soil Mechanics，35(1)： 1～6．

Qing N B. 2001. Prediction and forecast in rockbursts with fuzzy mathematical method[J]. Engineering Mechanics， (S)： 734～738．

Tang C A. 1993. Catastrophe in rock unstable failure[M]. Beijin： China Coal Industry Publishing House： 117～121．

Tan Tjongkie. 1987. Rockbursts， case records， theory and control[J]. Chinese Journal of Rock Mechanics and Engineering，1(6)： 1～18．

Tang Y A. 1989. Analysis of fractured face of rockburst with scanning electron microscope and Its progressive failure process[J]. Journal of Chinese Electron Microscopy Society，(2)： 41～48．

Tan Y L，Zhou H，Wang Y J，et al. 2002. PCA model for simulating AE and chaos in rock failure process[J]. The Chinese Journal of Nonferrous Metals，12(4)： 802～808．

The association academic department of China. 2011. Mechanism of rock burst[J]. Beijin： China Science and Technology Press．

Mamsurov V A. 2001. Prediction of rockbursts by analysis of induced seismicity data. International Journal Rock Mechanical Science and Technology，38： 893～901．

Wang J X. 1993. Theory ofelasticity[M]. Changsha： Central South University．

Wang M Y，Fan P X，Li W P. 2010. Mechanism of splitting and unloading failure of rock[J]. Chinese Journal of Rock Mechanics and Engineering，29(2)： 234～241．

Wen C P. 2008. Application of attribute synthetic evaluation system in prediction of possibility and classification of rockburst[J]. Engineering Mechanics，25(6)： 153～158．

Wu F Q，Wu J，Qi S W. 2010. Theoretical analysis on mechanism of rock burst of brittle rock mass[J]. Journal of Engineering Geology，18(5)： 589～595．

Xie H P，Pariseau W G. 1993. Fractal character and mechanism of rock bursts[J]. Chinese Journal of Rock Mechanics and Engineering，12(1)： 28～37．

Xu Z H，Xu X H，Tang C A. 1995. Theoretical analysis of a cusp catastrophe bump of coal pillar under hard rocks[J]. Journal of China Coal Society，20(5)： 485～491．

Zhang Y，Shi S W，He J D. 2016. Application of cloud model to engineering geology classification of surrounding rock mass of tunnel[J]. Journal of Engineering Geology，24(3)： 339～344．

Zhang Y B，Liu X X，Liang Z Z，et al. 2014. Experimental study of rock burst precursor of granite tunnel based on multi-physical field parameters[J]. Chinese Journal of Rock Mechanics and Engineering，33(7)： 1347～1357．

Brady B H G，Brown E T. 1990. 地下采矿岩石力学[M]. 北京：煤炭工业出版社.

陈宗基. 1987. 岩爆的工程实录、理论与控制[J]. 岩石力学与工程学报，1(6)： 1～18．

费文平，张国强，崔华丽. 2010. 高边坡卸荷岩体稳定性分析[J]. 武汉大学学报(工学版)，43(5)： 599～612．

冯夏庭，陈炳瑞，明华军，等. 2012. 深埋隧洞岩爆孕育规律与机制：即时型岩爆[J]. 岩石力学与工程学报，31(3)： 433～444．

何满潮，苗金丽，李德建，等. 2007. 深部花岗岩试样岩爆过程实验研究[J]. 岩石力学与工程学报，26(5)： 865～876．

兰天伟，张宏伟，韩军，等. 2012. 基于应力及能量条件的岩爆发生机理研究[J]. 采矿与安全工程学报，29(6)： 840～844， 875．

刘小明，李焯芬. 1997. 脆性岩石损伤力学分析与岩爆损伤能量指数[J]. 岩石力学与工程学报，16(2)： 140～147．

钱七虎. 2014. 岩爆、冲击地压的定义、机制、分类及其定量预测模型[J]. 岩土力学，35(1)： 1～6．

秦乃兵. 2001. 用模糊数学方法对岩爆进行预测预报[J]. 工程力学，(增刊)： 734～738．

唐春安. 1993. 岩石破裂过程的灾变[M]. 北京：煤炭工业出版社： 117～121．

谭以安. 1989. 岩爆岩石断口扫描电镜分析及岩爆渐进破坏过程[J]. 电子显微学报， (2)： 41～48．

谭云亮，周辉，王泳嘉，等. 2002. 模拟岩石声发射及混沌性的PCA 模型[J]. 中国有色金属学报，12(4)： 802～808．

王嘉新. 1993. 弹性力学[M]. 长沙：中南工业大学出版社．

王明洋，范鹏贤，李文培. 2010. 岩石的劈裂和卸载破坏机制[J]. 岩石力学与工程学报，29(2)： 234～241．

文畅平. 2008. 属性综合评价系统在岩爆发生和烈度分级中的应用[J]. 工程力学，25(6)： 153～158．

伍法权，伍劼，祁生文. 2010. 关于脆性岩体岩爆成因的理论分析[J]. 工程地质学报，18(5)： 589～595．

谢和平，Pariseau W G. 1993. 岩爆的分形特征和机理[J]. 岩石力学与工程学报，12(1)： 28～37．

徐曾和，徐小荷，唐春安. 1995. 坚硬顶板下煤柱岩爆的尖点突变理论分析[J]. 煤炭学报，20(5)： 485～491．

张勇，石胜伟，何江达. 2016. 基于云模型的隧洞围岩工程地质分类方法及应用[J]. 工程地质学报，24(3)： 339～344．

张艳博，刘祥鑫，梁正召，等. 2014. 基于多物理场参数变化的花岗岩巷道岩爆前兆模拟实验研究[J]. 岩石力学与工程学报，33(7)： 1347～1357．

中国科协学会学术部. 2011. 岩爆机理探索[M]. 北京：中国科学技术出版社．

JournalofEngineeringGeology工程地质学报 1004-9665/2016/24(5)- 0976- 05

UNLOADING TEST FOR ROCKBURST MECHANISM IN TUNNEL MODEL

With research on“surrounding rock￣roadway” system， the unloading rockburst can be recreated by the operation of horizontal stress unloading. The results indicate that the unloading rockburst has experienced evolution process of from “nonchalant stage to small particles ejection stage to flake off stage and to rockburst”.The tunnel model produces a number of the process from rockburst to stress adjust then to stress adjust failure and to another rockburst. At the end it forms “V”shape rockburst hole. In the condition of unloading， it exists some relationship between horizontal stress and fracture model. The unloading operation of tunnel model of distribution stress can be obtained from theoretical derivation. Vertical crack stress in different horizontal stresses(8.9MPa， 13.3MPa， 17.8MPa) is taken by modified Griffith failure criteria. The calculation model of “V”shape is established. At the stress point(13.3MPa) when the horizontal stress is under 13.3MPa， the relationship between horizontal stress and vertical crack stress has a positive correlation. When the horizontal stress is above 13.3MPa， the relationship between the horizontal stress and the vertical crack stress is a negative correlation. When the horizontal stress is at 13.3MPa， the strain energy concentrated area is the largest， and distance between this area and side wall is the minimum．

Rock mechanics， Unloading， Tunnel model， Rockburst

10.13544/j.cnki.jeg.2016.05.028

2016-05-30;

2016-07-26.

国家重大基础研究发展计划(973)项目(2014CB047100), 国家自然科学基金项目(51374088， 51574102, 51604117), 河北省钢铁联合基金项目(E2016209357)资助.

刘祥鑫(1987-)，男，硕士，讲师，主要从事矿山岩石力学的教学与研究工作. Email: liuxiangxin9@163.com

简介： 梁正召(1977-)，男，博士，教授，博士生导师，主要从事隧洞破裂失稳的研究工作. Email: LiangZZ@dlut.edu.cn

TD353

A