层状斜坡振动台实验的频谱特性研究*
李 果 华宏亮 赵建军
LI Guo① HUA Hongliang① ZHAO Jianjun②
层状斜坡振动台实验的频谱特性研究*
李 果①华宏亮①赵建军②

本文通过大型振动台试验,对硬岩顺层、反倾和软岩顺层、反倾4类结构岩体边坡的地震动力响应的频谱特性进行了分析。实验结果表明:传递至坡肩的振动信号,是一个包含了斜坡本身材料和结构特征的复杂信号集合。对这一信号的傅里叶频谱进行分析获得的特征信息,与斜坡本身的结构特性吻合,说明在振动台试验中采用这一方法对斜坡结构进行研究是可行的。在本次试验中,当不同频率的垂直向震动施加于边坡时,坡肩衍生振动频率的幅值呈现了明显的反倾高于顺层,硬岩高于软岩的特性; 而水平震动施加于边坡时,则硬岩顺层,软岩反倾斜坡具有更高的幅值,频率也更集中于特定的卓越频段,而硬岩反倾和软岩顺层斜坡的水平震动响应则相对不显著。另外,硬岩顺层斜坡对震动的响应表现比软岩顺层明显,而软岩反倾的反应比硬岩反倾明显。当施加垂直向天然波信号时,顺层斜坡的傅里叶频谱图像与台面波形基本保持一致,而反倾斜坡表现为对特定频率段的幅值放大更加显著。水平向加载天然波信号时各个斜坡呈现了更多的一致性,表明此工况下坡体结构与岩性的影响则明显较不显著。
振动台试验 频谱特性 失稳机理 动力响应特征 坡体结构
LI Guo①HUA Hongliang①ZHAO Jianjun②

0 引 言
层状结构是一类较为特殊的斜坡结构,层状结构的边坡灾害也是极为常见的边坡灾害类型。由于此类斜坡显著的结构面控制特征,导致传统的基于土质边坡的分析研究手段在这类边坡的分析与评估中产生了一定的局限。因而,开展针对性的专项研究就十分必要。
统计表明, 2008年的 “5·12” 汶川地震在龙门山地区触发的崩塌滑坡中,近60%出现在具有层状结构的岩石边坡中(黄润秋, 2008; 李果等, 2011)。通过大型振动台物理模拟实验这一手段,可以对这类斜坡的动力响应机理,破坏特征及机理进行直观的研究和分析。近年来,对于这类大型模型实验的相关研究和分析多集中于破坏特征及相关过程演化的描述,应力、加速度计等传感器数据与时间关系的线性描述(许强等, 2010; 董金玉等, 2011),以及对于加速度放大效应的论述(祁生文等, 2003),对于模型边坡频谱特性的关注则相对较少。蒋良潍等(2008),徐光兴等(2008)曾结合加速度传递函数对边坡模型的频率与阻尼特性进行了分析论证,探讨了相关特性与边坡本身振动性质之间联系,取得了较好的效果。
本文尝试对模型结构在地震过程中的频谱特性开展研究,通过对相关数据的深入分析与挖掘,分析模型结构本身与传感器记录结论的相关联系,建立地震条件下层状结构岩体边坡的破坏机理与其本身结构之间的联系。
1 振动台模型设计
1.1 模型设计
为了方便进行对比分析,本次模型试验建立了4个层状岩体边坡 (图1),分别为硬岩顺层斜坡和硬岩反倾斜坡; 软岩顺层斜坡和软岩反倾斜坡。模型比例尺为1︰100,坡面为直线坡,坡度60°,岩层倾角也取60°。
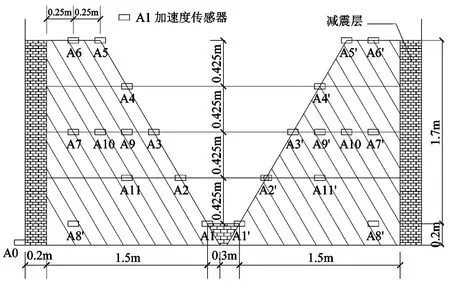
图1 模型及监测点布置图
1.2 相似关系设计与材料配比
根据相似理论(袁文忠, 1998; 罗先启等, 2008),设计了如表1所示的模型相似关系,选取重晶石粉,石英砂,石膏,甘油,水和机油,以表2为设计参数,以表3为比例进行模型的制备。
表1 模型相似关系
Table1 Similarity relations of the model

物理量相似关系相似常数几何尺寸LCL=100(控制量)100密度ρCρ(控制量)1振动加速度aCa=1(控制量)1容重γCγ=Cρ1弹性模量ECE=CρCL100泊松比μCμ=11摩擦系数CfCf=11内聚力CCC=CρCLCa100内摩擦角ΦCΦ=11
表2 材料参数
Table2 Model material parameters

岩性灰岩千枚岩原型模型原型模型密度/kN·m-326.5~27.52726~2726静弹模/MPa6000~900073.71000~300024.1泊松比0.250.250.280.28抗剪/MPa5~500.120.5~50.043内摩擦角/(°)38~454330~3835层面抗剪/MPa0.5~1.00.0060.05~0.50.001层面内摩擦角/(°)35~403725~3025
表3 材料配比
Table3 Model material mixing ratio

材料/%重晶石砂子石膏甘油水机油软岩51.332.19.06.41.30硬岩43.230.912.38.61.23.7
1.3 模型建造与加载工况设计
制成的模型长3.7m,宽1.7m,高1.2m(图2)。

图2 刚性模型箱中建成的模型
模型建造完成后,通过振动台加载设计的地震波,本次加载的地震波分为两阶段:第1阶段为低振幅(0.1~0.2g)的正弦波和天然波,第2阶段则逐步增强天然波振幅(0.3~1.0g),在振动过程中,以低幅值(0.05g、0.1g)的白噪声扫描。
模型中共布设了42个加速度传感器 (图1),及位移和压力传感器若干。后期数据处理中发现,位移及压力传感器数据基本无法使用,分析其原因为此类传感器需要两端固定才能准确采集,但在振动环境中却难以保持稳定,因此不建议在同类实验中布设此类传感器。
2 正弦信号的频谱特性研究
从波形上来看,正弦波为一周期性信号,具有固定的振幅和频率,在后期信号处理过程中能够避免天然波中复杂信号的干扰,简单直观地了解地震波在模型中传播过程中所发生的变化。本次实验设计了3种频率的正弦地震波,分别为5Hz, 10Hz和15Hz和两种振幅0.1g、0.2g进行加载。
图3 为0.1g垂直向正弦波加载工况,从上至下依次为台面,硬岩顺层坡顶,硬岩反倾坡顶,软岩顺层坡顶和软岩反倾斜坡的坡肩(A5)监测点的加速度时程曲线。可以看出,传递至坡顶的加速度曲线仍基本保持正弦波形。从这一图形中,我们难以直观的看出各个波形的差异,因此,通过傅立叶变换将时域信号转为频域信号进行分析,以便研究各类边坡中地震波传播过程中发生的信号激发和衰减及其对斜坡的影响。
台面监测点的快速傅立叶变换(FFT变换)获取的频谱特性如图4、图5所示,由于是正弦波,具有单一的基础频率,所以其FFT谱为一条垂直直线。而对于坡顶各点,由底部输入的震动经过介质的传递,材料界面的吸收、反射和折射等各种效应的综合作用,最终形成一个以输入基频为主,同时具有整数倍等特征频率,并包含各种杂讯的复杂信号。
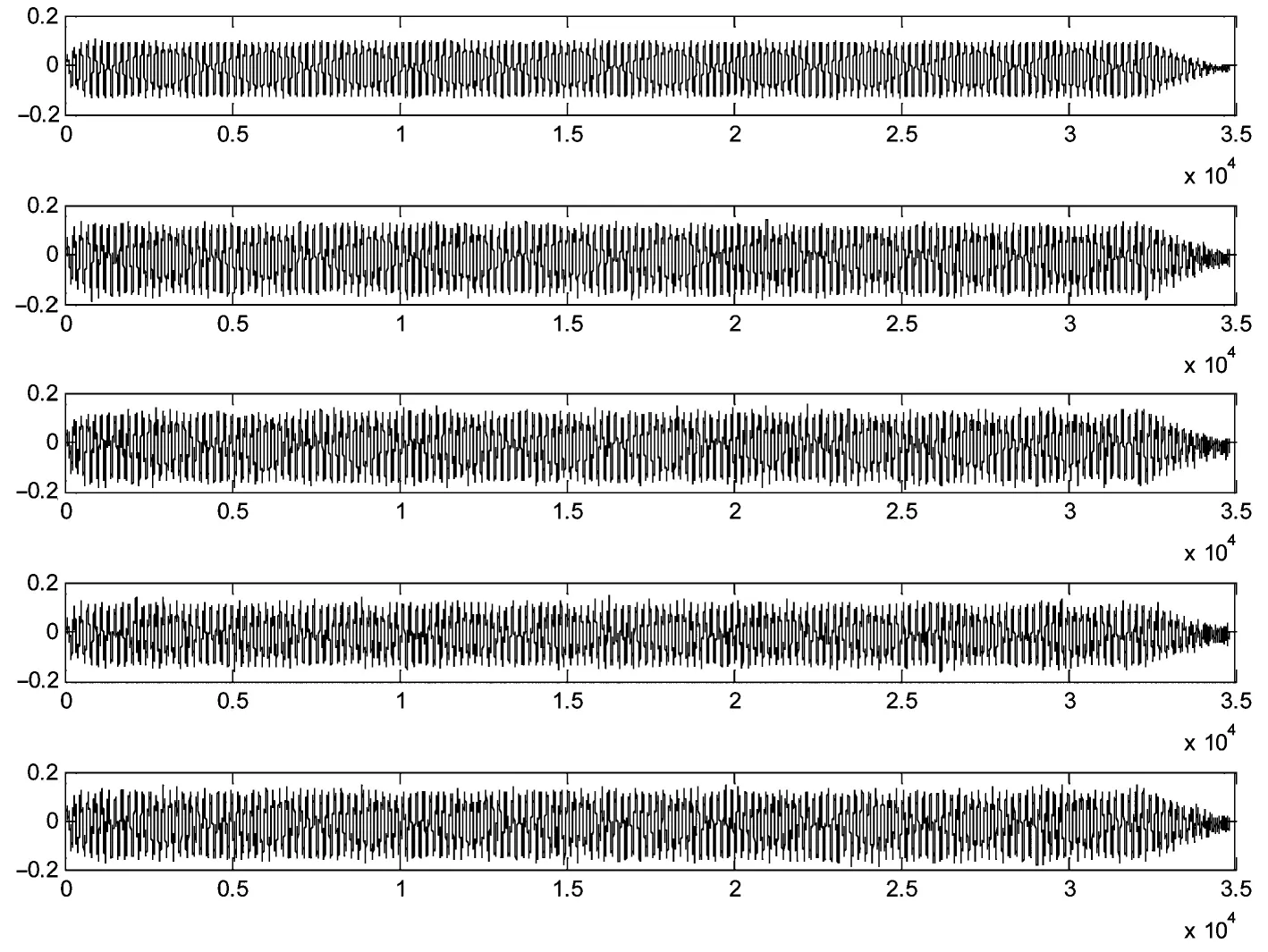
图3 0.1g 垂直向正弦信号输入时台面及坡肩各点监测波形

图4 台面0.1g水平向震动FFT谱

图5 台面0.1g垂直向震动FFT谱
对于坡形、岩性、结构完全相同的边坡模型来说,采用单一频率加速度震动所获取的傅立叶谱理论上是完全相同的,然而本次实验所建立的4个边坡模型,其岩性、坡体结构均不相同,经过加速度震动反应后,其坡肩部位的动力响应特征也存在显著区别。图6~图8反映了垂直向0.1g正弦加速度震动工况下斜坡坡肩部位监测点激发卓越频率的傅立叶谱图像,反映了地震波在坡内传播后传递至斜坡坡肩部位的频谱特性,图中从左至右依次为硬岩顺层斜坡,硬岩反倾斜坡,软岩顺层斜坡和软岩反倾斜坡。

图6 垂直向5Hz激发卓越频率傅立叶谱

图7 垂直向10Hz激发卓越频率傅立叶谱

图8 垂直向15Hz激发卓越频率傅立叶谱

图9 水平向5Hz激发卓越频率傅立叶谱
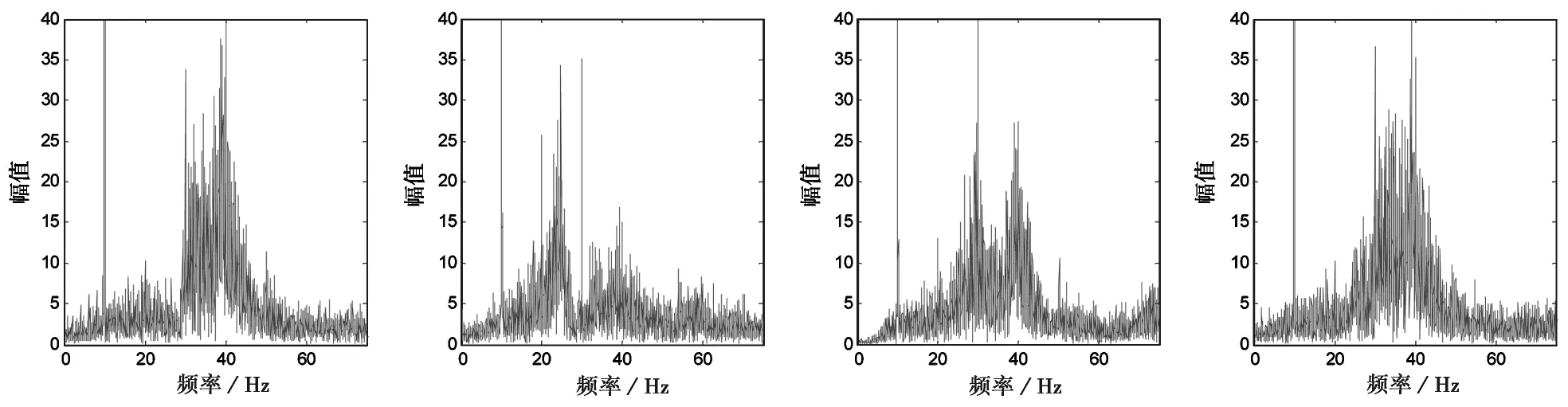
图10 水平向10Hz激发卓越频率傅立叶谱

图11 水平向15Hz激发卓越频率傅立叶谱

图12 0.1g天然波台面信号傅立叶振幅谱

图13 垂直0.1g天然波激振工况垂直向傅立叶振幅谱

图14 水平0.1g天然波激振工况水平向傅立叶振幅谱
从图中可以看出,当施加5Hz, 10Hz, 15Hz的垂直向震动时,对于硬岩顺层斜坡模型来说,显著的衍生频率位于45Hz, 70Hz附近,而对于硬岩反倾位于60Hz附近,软岩顺层位于50Hz及70Hz附近,软岩反倾位于70Hz附近。
而对于水平向震动(图9,图10,图11),则分别为: 硬岩顺层斜坡位于40Hz,硬岩反倾斜坡25Hz附近,软岩顺层位于30Hz及40Hz附近,软岩反倾位于40Hz附近。
观察这些衍生频率的卓越频段,可以发现,对同一输入信号来说,垂直向震动衍生频率的幅值明显呈现反倾高于顺层,硬岩高于软岩的特性。 也就是说在垂直向震动作用于边坡时,硬岩斜坡的地震动力响应过程中,斜坡上部介质运动较软岩斜坡更加剧烈,同时反倾斜坡也比顺层剧烈。这一结果也解释了在2008年汶川地震灾区,靠近发震断裂带附近发育的大量大型反倾滑坡破坏的现象,即发震断裂附近的垂直向剧烈震动,对反倾斜坡这一传统认识上稳定的斜坡结构存在不利影响。
当频率升高时,这一规律没有显著变化。施加水平向正弦震动过程中,硬岩顺层,软岩反倾斜坡具有更高的幅值,频率也更集中于特定的卓越频段,而硬岩反倾和软岩顺层则不显著。同时,硬岩顺层的响应比软岩顺层明显,而软岩反倾的反应则强于硬岩反倾。
上述现象充分表明了坡体结构和岩性的差异对于边坡动力响应特征的显著影响。
3 天然波信号的频谱特性研究
与正弦波不同,天然波是具有多种频率与振幅的复杂波形,本次实验选取的地震波是2008年汶川地震过程中,台站获取的真实波形(国家地震科学数据共享中心, 2008)。观察如图12 所示的台面监测数据的傅里叶频谱,可以看出输入的垂直向震动信号卓越频率位于25~40Hz之间,水平信号则位于较为低频的2~5Hz频段。我们同样将坡肩信号进行处理,获取其傅里叶频谱图像分别如图13、图14所示。
可以看出,对于0.1g的垂直向的震动来说,4类斜坡模型分别表现了不同的频谱放大特性。硬岩顺层斜坡的傅里叶频谱图像与台面信号基本保持一致。硬岩反倾则表现了显著的较低频放大(10~15Hz),软岩顺层斜坡的频谱图像与硬岩顺层接近,但由于其岩性软弱,其卓越频段的放大幅值明显高于硬岩顺层斜坡。而对于软岩反倾斜坡来说,除了与硬岩反倾类似的较低频放大外,其较高频频段也具备了明显的放大现象。可以明显地看出,对于垂直向的震动来说,软岩斜坡的卓越频率幅值放大更为显著。显然,当加速度幅值增强时,其坡体所受的损伤也必然更加剧烈。另外,反倾斜坡并未产生显著的放大,反而硬岩顺层斜坡在较高频的25~35Hz段产生了显著的衰减,可以认为,此类结构的斜坡,其斜坡结构的控制作用更为显著。其次我们也可以观察到,受斜坡结构的影响,反倾在斜坡较低频的10~15Hz频段出现了显著的频幅放大,软岩斜坡的响应尤为剧烈。
同样的,观察0.1g水平向震动,我们发现,4类斜坡的频谱放大,均保持了与台面信号相似的波形。在10Hz频段上,呈现了类似显著的幅值放大现象,即是水平加载条件下受斜坡结构的控制不甚显著,信号本身的作用更加明显。这也解释了我们对于地震滑坡的通常认识:由于传递至坡顶的水平震动信号的卓越频率更为集中,表明能量也更为集中,坡体结构的差异对信号的影响较为轻微,因此,水平震动可以在各类斜坡中上部均可造成相比垂直震动更为显著的破坏。
如果对图13 及 图14 的波形进行对比观察,可以发现在垂直和水平两种加载工况下,硬岩反倾斜坡卓越频段的吻合程度明显好于顺层斜坡。从能量传递的观点来看,由于更多的地震能量未能在传递过程中消耗,自坡脚输入的震动能量可以传递至相对坡脚更远的位置,从而造成更多的大规模斜坡失稳。
4 结 论
振动台实验是认识地震条件下斜坡动力响应特征的有力工具,但受限于震动过程的瞬时特性,通过肉眼观察或响应记录的直观分析等手段毕竟存在一定的局限,对震动相关的监测数据的深入分析,是获取对整个动力响应过程深入认识的有效途径。本文通过对层状斜坡大型振动台实验加速度监测数据频谱特性的研究,取得了如下的主要认识与结论:
(1)对于特定结构的斜坡来说,传递至斜坡表面的震动信号,是地震波在斜坡内部衰减、折射和反射之后形成的复杂信号,斜坡本身的材料和结构的差异,也同时反应在这一信号当中。
(2)当施加不同频率正弦信号作用于斜坡时,比较激发信号的傅里叶频谱的卓越频段与原始信号的傅里叶频谱可以明显的看出,顺层斜坡对于水平震动的响应更加显著,而反倾斜坡则更易受垂直向震动影响,这和我们的认识是吻合的。
(3)当施加天然波信号时,我们获得了与正弦信号相似的结论,这也说明了即斜坡的材料与结构特性,是影响动力斜坡响应的控制性因素。
(4)综合垂直震动和水平震动和的频谱图像,结合能量观点,可以较好地解释汶川地震过程中,具有有利结构的反倾斜坡却多发大规模滑坡灾害的地质现象。
CENC. 2008. China Earthquake Data Center[EB/OL]. http:∥data.earthquake.cn.
Dong J Y,Yang G X,Wu F Q,et al. 2008. The large-scale shaking table test study of dynamic response and failure mode of bedding rock slope under earthquake[J]. Rock and Soil Mechanics,32(10): 2977~2976.
Xu G X,Yao L K,Gao Z N,et al. 2008. Large-scale shaking table model test study on dynamic characteristics and dynamic responses of slope[J]. Chinese Journal of Rock Mechanics and Engineering,27(3): 624~632.
Huang R Q,Li W L. 2008. Research on development and distribution rules of geohazards induced by Wenchuan earthquake on 12th May, 2008[J]. Chinese Journal of Rock Mechanics and Engineering,27(12): 2585~2592.
Jiang L W,Yao L K,Wei W,et al. 2008. Transfer function analysis of earthquake simulation shaking table model test of side slopes[J]. Rock and Soil Mechanics,31(5): 1368~1374.
Li G,Huang R Q,Ju N P,et al. 2011. Study of distribution and development laws of secondary disaster in Longmenshan Area after earthquake[J]. Yangtze River,42(4): 23~28.
Liu J,Ba J,Ma J W,et al. 2010. Seismic wave attenuation rule in random pore media[J]. Science China,40(7): 858~868.
Luo X Q,Ge X R. 2008. Theory and application of model test on landslide[M]. Beijing: China Water & Power Press: 16~28.
Qi S W,Wu F Q, Sun J Z. 2003. Study on dynamic responses of slope[J]. Science in China,33(B12): 28~40.
Xu Q,Liu H X,Zou W,et al. 2010. Large-scale shaking table test study of acceleration dynamic responses characteristics of Slopes[J]. Chinese Journal of Rock Mechanics and Engineering,29(12): 2420~2428.
Yuan W Z. 1998. Simulation theory and static model test[M]. Chengdu: Southwest Jiaotong University Press: 18~21.
中国地震台网中心. 2008. 国家地震科学数据共享中心[EB/OL]. http:∥data.earthquake.cn/.
董金玉,杨国香,伍法权,等. 2011. 地震作用下顺层岩质边坡动力响应和破坏模式大型振动台试验研究[J]. 岩土力学,32(10): 2977~2982.
徐光兴,姚令侃,高召宁,等. 2008. 边坡动力特性与动力响应的大型振动台模型试验研究[J]. 岩石力学与工程学报,27(3): 624~632.
黄润秋,李为乐. 2008. “5·12” 汶川大地震触发地质灾害的发育分布规律研究[J]. 岩石力学与工程学报. 27(12): 2585~2592.
蒋良潍,姚令侃,吴伟,等. 2010. 传递函数分析在边坡振动台模型试验的应用探讨[J]. 岩土力学,31(5): 1368~1374.
李果,黄润秋,巨能攀,等. 2011. 龙门山地区震后次生灾害发育分布规律研究[J]. 人民长江,42(4): 23~28.
刘炯,巴晶,马坚伟,等. 2010. 随机孔隙介质中地震波衰减分析[J]. 中国科学(物理学力学天文学),40(7): 858~868.
罗先启,葛修润. 2008. 滑坡模型试验理论及其应用[M]. 北京:中国水利水电出版社: 16~28.
祁生文,伍法权,孙进忠. 2003. 边坡动力响应规律研究[J]. 中国科学,33(B12): 28~40.
许强,刘汉香,邹威,等. 2010. 斜坡加速度动力响应特性的大型振动台试验研究[J]. 岩石力学与工程学报,29(12): 2420~2428.
袁文忠. 1998. 相似理论与静力学模型试验[M]. 成都:西南交通大学出版社: 18~21
JournalofEngineeringGeology工程地质学报 1004-9665/2016/24(5)- 0967- 09
SPECTRUM CHARACTERISTICS OF STRATIFIED ROCK SLOPES USING SHAKING TABLE TEST
By means of large-scale shaking table test, this paper analyzes the dynamic response of stratified hard rock and soft rock slopes with anti-dipping strata or dipping strata subject to strong earthquakes. The results show that: the seismic signal of the slope shoulder contains the characteristic of the slope structure and material. The processed signal using Fast Fourier Transform Algorithm contains some feature of the slope itself. This method is practical in the shaking table test. The FFT spectrum of discrete frequency signal shows that the derivative frequency of the anti-dip slope is higher than that of the dip slope under the vertical seismic force. And as horizontal seismic force is applied, the hard rock dip slope and the soft rock anti-dip slope have higher magnitude and their predominant frequency is more concentrated than those the hard rock anti-dip and soft rock dip slope. The seismic response of the hard rock dip slope is more significant than that of the soft rock dip slope. As a natural earthquake record is applied to the model vertically, the FFT spectrum of the dip slope has the same pattern as the shaking table, and the anti-dip slope has more magnification in certain frequency. While a horizontal natural record is applied, the four models show more consistency, which means at this condition, the influence of structure and the lithology are non-significant.
Shaking table test, Spectrum characteristic, Failure mechanism, Dynamic response of slopes, Slope structure
10.13544/j.cnki.jeg.2016.05.027
2015-09-18;
2016-06-30.
NSFC-云南联合基金重点支持项目(U1402231)资助
简介: 李果(1981-),男,博士,高级工程师,主要从事工程地质、岩土工程及公路工程相关研究工作. Email: ziltch2002@163.com
P642.22
A

