基于模糊数学理论的压滤车间绩效评价模型

高 建，张立海，朱再胜

(淮南矿业集团选煤分公司，安徽 淮南 232000)

基于模糊数学理论的压滤车间绩效评价模型

高 建，张立海，朱再胜

(淮南矿业集团选煤分公司，安徽 淮南 232000)

为了实现压滤车间生产绩效评价的科学化和合理化，通过对选煤厂压滤车间绩效评价分析，选取浓缩池煤泥层厚度、压滤板数、原煤入选量三个主要因素作为评价指标；运用层次分析法和模糊数学理论确定模糊综合评价模型，进而提出基于模糊数学的压滤车间绩效评价模型，并采用该模型对朱集东选煤厂压滤车间各班的生产绩效进行评价。实践结果表明：该模型具有较强的适用性，能够客观地反映压滤车间各班的生产绩效情况。

模糊数学；压滤车间；绩效评价模型

耙式浓缩机是煤泥水处理中常见的主力设备，如果浓缩过程中煤泥层过厚，就会使耙架受损或传动装置负荷过大，进而引发生产事故。淮南矿业集团选煤分公司规定：浓缩机压耙属于重大机电事故和生产责任事故，故朱集东选煤厂对此非常重视。朱集东选煤厂是一座大型动力煤选煤厂，设计能力为4.0 Mt/a，二段浓缩选用两台并联的GZN-45周边传动耙式浓缩机，另一台净化浓缩机为中心传动的NXZ-20耙式浓缩机。在原煤灰分和入选比例高、煤泥含量大时，该选煤厂要求压滤车间积极处理浓缩池中的煤泥，确保系统持续、安全运行。

但目前还没有科学、合理评价压滤车间生产绩效的方法，而煤泥层厚度单个指标不足以正确评价压滤车间一个班的工作绩效。国内外对工作绩效评价方法的研究很多[1-7]，而评价煤泥处理工作绩效是一个复杂的系统工程，涉及多方面的因素，且这些因素之间相互联系，相互制约。为此，通过对压滤车间工作绩效分析，选取浓缩池煤泥层厚度、压滤板数、原煤入选量三项考核指标，基于层次分析法和模糊数学理论建立压滤车间绩效评价模型，并采用该模型对其进行综合评价，以期实现压滤车间工作绩效评价的科学化和合理化，也为压滤车间工作绩效评价方法的研究提供一个新思路。

1 综合评价模型的构建

每班处理的浓缩池煤泥层厚度(以下简称“煤泥层厚度”)是指每个生产班交班时的煤泥层厚度减去接班时的煤泥层厚度，各班处理的煤泥层厚度值越小越好，负值更好，这意味着该生产班已处理完本班生产的煤泥，甚至更多的煤泥。

从多个方面判断压滤车间工作绩效的大小，选取与煤泥压滤相关的三个指标来反应工作的综合质量。煤泥来源于选煤生产，在煤粉含量不变的情况下，原煤入选量越大，产生的煤泥越多，这就要求压滤车间加快处理速度。压滤板数(煤泥产量)可以直接反映压滤车间的工作量，压滤板数越多，需要处理的煤泥量越大。煤泥层厚度能够直接反映各生产班工作期间浓缩池中积聚的煤泥量[8]。一级综合评价模型如图1所示。

图1 一级综合评价模型

2 通过层次分析法确定权重

在多指标评价中，常见的优先权重分配法有三种[9-10]。第一种为客观法，即利用属性来确定指标的优先权重，如主成分分析法、离差及均差法等；第二种为主观法，即由决策人员依照各指标的主观重视程度进行权重的分配，如层次分析法(AHP)[11-13]、比较矩阵法等；第三种为组合赋权法，是有些学者将主观法与客观法相结合而得到的。由于生产实际中工作绩效大小的判断具有主观性和不确定性，故选用AHP来确定指标的权重。

2.1 指标重要性的比对

在指标数n≥3时，任何专家都可能很难判断出一组确切的数据，但可以通过两两比较来确定。采用函数f(x,y)表示对总体而言，指标x比指标y的重要性标度；选用函数f(y,x)表示对总体而言，指标y比指标x的重要性标度，两个指标的判断列表如表1所示。

根据本行业专家确定的比较结果为：煤泥层厚度稍微重要于压滤板数，也稍微重要于原煤入选量，压滤板数比原煤入选量的重要性介于同等和稍微之间。

表1 指标x与y判断列表

2.2 计算判断矩阵

将本行业专家给出的指标综合比对后的描述写入重要性的描述矩阵中，具体如下：

将该描述矩阵转化为判断矩阵A，

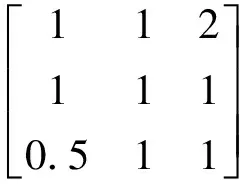
2.3 计算权重集

目前，研究者们提出的计算方法很多，大致可分为两类。一类是近似计算法，主要是通过判断矩阵元素之间的代数运算或基于特征向量法导出指标的权重集，如特征向量法、和法、根法等。另一类是最优化排序法，主要是通过求解一个最优问题得到指标的权重集，如最小二乘法、线性规划法等[14-15]。在判断矩阵一致时，这些方法可以得到精确的解[16-17]，由于和法较易操作，故选用和法计算权重。

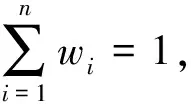
(1)

通过计算可得：w1=0.41，w2=0.33，w3=0.26，所以权重集为w=(0.41,0.33,0.26)T。

2.4 验证一致性

由于种种客观条件的限制，该判断矩阵不可能是绝对可靠的，要全面衡量其可靠性很困难，但至少要求判断矩阵不出现明显“矛盾”，导致判断结果不一致，所以要检测该判断矩阵是否具有一致性。为此，引入一致性指标Consistency index(CI)，对于任意的判断矩阵A，都有CI≥0，当且仅当CI=0时判断矩阵A具有一致性；而CI值越小，判断矩阵A偏离一致性的程度越大。

按照式(2)、式(3)计算判断矩阵A的第一特征值λ1和一致性指标CI，

(2)

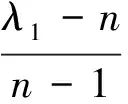
(3)

通过计算可得λ1=3.054，CI=0.027。

为此，再引入随机一致性指标Random index(RI)。RI的计算方法为：固定n值，随机生成若干个n阶正互反矩阵，一一计算各矩阵的CI值，并将其平均值作为RI。计算出来的3～10阶判断矩阵的随机一致性指标如表2所示。

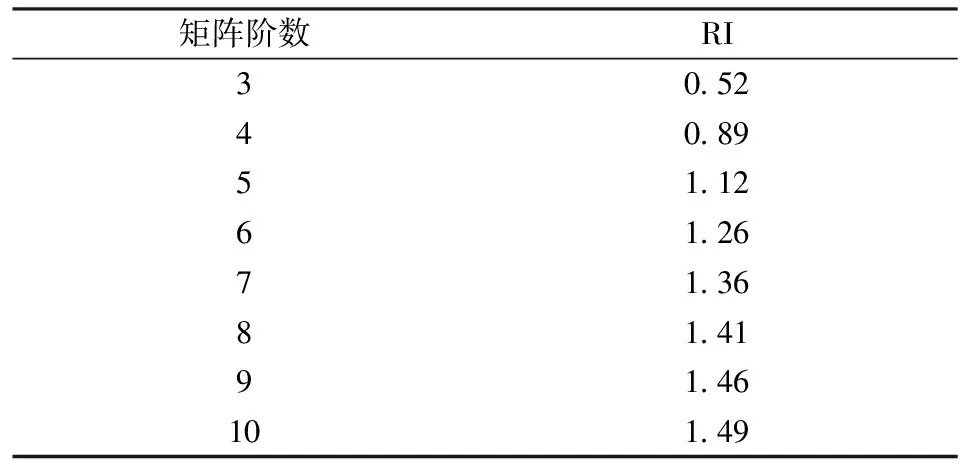
表2 3～10阶判断矩阵的随机一致性指标

结合不同阶数的随机一致性指标RI值，计算出一致性比率Consistency ratio(CR)，计算式为:

(4)

对于给定的判断矩阵A=(aij)n×n，当且仅当CR<0.1时，A满足一致性要求。以λ1所对应的归一化后的特征向量作为归一化权向量。

通过表2可知：三阶判断矩阵的随机一致性指标RI=0.52，计算出的判断矩阵A的一致性比率CR=0.052，且小于0.1，故判断矩阵A可靠，具有一致性。

3 模糊综合评价体系的构造

1965年扎德教授(ZADEH L Z)首次提出了Fuzzy set的概念，创建了模糊数学[18]。模糊集使元素以一定程度隶属于集合，元素属于集合的程度由“0”与“1”之间的一个数值——隶属度来描述，而把一个元素映射到一个适当地隶属度则由隶属度函数来实现[19]。

3.1 确定评价集及各评价指标的值域

朱集东选煤厂对压滤车间的生产情况进行了详细统计，1月份各生产班的工作绩效如表3所示。

表3 各班工作绩效

以1班的工作绩效数据为例，该月处理的煤泥层厚度累计值为-1.2 m，压滤煤泥累计板数为825板，每板煤泥质量约为14.5 t，即处理的煤泥量约为11 963 t，主厂房原煤入选量为105 818 t。由上述数据可知：压滤车间1生产班工作绩效评价集为U={W1,W2,W3}={-1.2,825,105 818} 。

根据连续数个月的统计数据可知：各班处理的煤泥层厚度最小值为-6.7 m，最大值为4.2 m，故定义W1的值域范围为[-10，10]。根据月生产计划和原煤中的粉煤含量，可以大概算出某月压滤车间需要处理的煤泥板数；某月计划入选原煤420 000 t，高灰煤泥含量约占11%，需要处理的煤泥板数约为797板，故定义W2的值域范围为[700，900]。根据月生产计划，平均分配到4个生产班，故可定义原煤入选量W3的值域范围为[100 000，120 000]。

3.2 确定隶属度函数

随着原煤入选量的增大，煤泥产量和煤泥层厚度也增大，压滤车间的工作量随之增大，故研究中选用直线型隶属度函数[20]。由于指标W1是成本型指标，其值越小越好；W2与W3都是效益型指标，其值越大越好。因此，这三者采用的隶属度函数存在些许不同，式(5)、式(6)、式(7)依次为W1、W2、W3的隶属度函数。

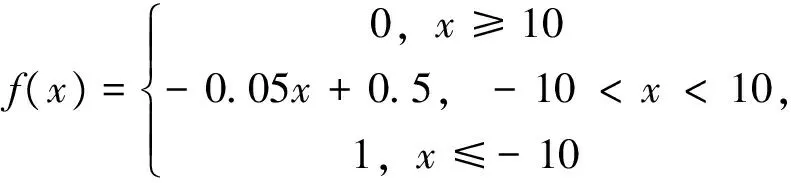
(5)

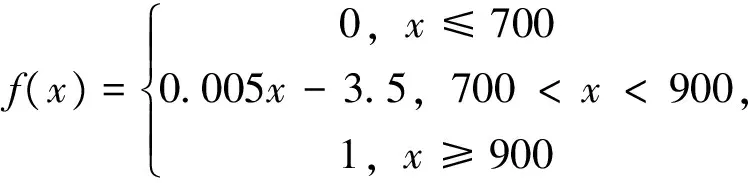
(6)

(7)

3.3 指标的模糊转化

将试验结果的各指标值通过隶属度函数模糊转化为隶属度μ(μ∈[0,1])，以W1为例说明具体操作过程。1班1月处理的煤泥层厚度累计值为-1.2 m，因为-10<-1.2<10，代入隶属度函数后可得P1=0.56。

依次可计算出W2、W3的隶属度P2、P3，其值分别为0.625、0.290 9。因此，压滤车间1班1月工作绩效各指标的模糊评价集为P=(0.56,0.625,0.290 9)。

3.4 多指标的综合评价

多指标的综合评价指标为各指标的模糊评价集与各指标权重分配集的矩阵乘积，压滤车间1班的工作绩效综合评价指标值为：

Z(1)=P1×3·W3×1=(0.56,0.625,0.290 0)×

(0.41,0.33,0.26)T=0.51。

按照相同的方法，可以计算出压滤车间2班、3班、4班的工作绩效综合评价指标值，其值分别为Z(2)=0.22、Z(3)=0.35、Z(4)=0.46。

根据以上分析可知Z∈[0,1]，Z(1)、Z(2)、Z(3)、Z(4)是考查压滤车间各生产班工作绩效三种指标后得到的综合评价指标值，据此对各生产班的工作绩效进行评比，其值越大说明业绩越好。Z(2)

4 结语

对朱集东选煤厂压滤车间工作绩效的评价实践表明：基于煤泥层厚度、压滤板数、原煤入选量三个指标的综合评价模型，具有较强的适用性，能够客观反映压滤车间各生产班的生产业绩。基于层次分析法的模糊综合评价体系可以解决各指标间的不协调性，能够提供可操作性强且实用的全面反映压滤车间工作绩效的评价模型，这可为压滤车间工作绩效评价方法的研究与应用提供一个新思路。

[1] 张跃松,黄志烨,谢宇宁.基于DEA的建筑业上市公司绩效评价[J].土木工程学报,2012(S2): 331-336.

[2] 雷星晖,尤筱玥.基于层次分析法支持决策的外包服务供应商绩效评价[J].同济大学学报：自然科学版, 2014 (11): 1770-1775.

[3] 罗文斌,吴次芳.农村土地整理项目绩效评价及影响因素定量分析[J].农业工程学报,2014,30(22):273-281.

[4] AKDAG H，KALAYCL T，KARAGOZ S, et al. The evaluation of hospital service quality by fuzzy MCDM [J]. Applied Soft Computing, 2014, 23 (23):239-248.

[5] BUTNARU G I,TEFNICM, MAXIM G M. Alternative Method of Quality Evaluation in Tourism. Case Study Applied in Tourist Accommodation Units [J]. Procedia Economics and Finance, 2014 (15):671-678.

[6] CHEN J F, HSIEH H N, DO Q H. Evaluating teaching performance based on fuzzy AHP and comprehensive evaluation approach [J]. Applied Soft Computing, 2015 (28): 100-108.

[7] 王迎超,尚岳全,孙红月,等.基于功效系数法的岩爆烈度分级预测研究[J].岩土力学, 2010,31(2): 529-534.

[8] 赵拴明.优化煤泥水浓缩压滤系统项目的可行性分析[J].煤炭科学技术,2011(S1):102-126.

[9] 朱再胜.含钾页岩球磨超细粉碎及工艺优化[D]. 徐州：中国矿业大学, 2012.

[10] 兰继斌. 关于层次分析法优先权重及模糊多属性决策问题研究 [D]. 成都：西南交通大学, 2006.

[11] SAATY T L. What is the Analytic Hierarchy Process? [M]. Springer Berlin Heidelberg, 1988.

[12] 孟志斌. 基于层次分析法的矿井通风系统改造[J]. 煤炭科学技术,2013(S1). 78-81.

[13] 刘开第,庞彦军,金 斓.对AHP单准则排序方法的改进[J].数学的实践与认识,2015(12)： 207-214.

[14] 王长青,张一农,许万里. 运用最小二乘法确定后评估指标权重的方法 [J].吉林大学学报：信息科学版, 2010,28(5): 513-518.

[15] 李汶华,郭均鹏.判断矩阵的区间权向量及其方案排序[J].哈尔滨工业大学学报, 2005，37(5)：698-700.

[16] 叶 珍.基于AHP的模糊综合评价方法研究及应用[D].广州：华南理工大学, 2010.

[17] 余明江.排序向量的三个近似解系研究[J].安徽工程科技学院学报：自然科学版, 2004, 19(2): 20-23.

[18] ZADEH L A. Fuzzy sets [J]. Inform and Control,

1965, 8(65):338-353.

[19] 胡宝清. 模糊理论基础(第二版)[M]. 武汉: 武汉大学出版社, 2010.

[20] 杨家豪,欧阳森,石怡理,等.一种组合隶属度函数及其在电能质量模糊评价中的应用[J].电工电能新技术,2014,33(2):63-69.

Fuzzy mathematics theory-based model for evaluation of operating performance of filter press shop

GAO Jian, ZHANG Li-hai, ZHU Zai-sheng

(Coal Preparation Branch of Huainan Mining Group, Huainan, Anhui 232000, China)

In order to enable the operating performance of the filter press shop to be evaluated on a scientific and rational basis, an analysis is made of the factors involved in evaluating the operating performance of the filter press shop in Zhujidong Coal Preparation Plant, and finally, 3 factors, viz: thickness of slime layer in thickener, number of plates of filter press and proportion of raw coal treated, are selected as evaluation criteria. Following the determination of an appropriate fuzzy comprehensive evaluation model based on analytic hierarchy process (AHP) and fuzzy mathematics theory, a fuzzy mathematics-based model is then proposed for the evaluation of the operating performance of the filter press shop of the plant on a shift by shift basis. Practice shows the model is highly adaptable and can objectively reflect the operating performance of each shift.

1001-3571(2016)01-0087-04

TD946.2；F279.13

A

Keywordsfuzzy mathematics; filter press shop; operating performance evaluation model

2016-02-08

10.16447/j.cnki.cpt.2016.01.023

高 建(1983—)，男，山东省济南市人，工程师，从事选煤工艺技术研究与选煤生产管理工作。

E-mail：longinces@126.com Tel：13309641890