基于MATLAB的转运溜槽设计

朴香兰

(延边大学 工学院，吉林 延吉 133002 )

基于MATLAB的转运溜槽设计

朴香兰

(延边大学 工学院，吉林 延吉 133002 )

转运溜槽是物料输送链中的连接部件，在运输系统中起着导向和分流的作用。为了提高转运溜槽几何尺寸选择的准确性，保证物料流动畅通，对其中的物料进行运动分析，并建立物料流动模型。采用回归正交试验设计方法，基于MATLBA程序进行试验，建立转运溜槽的回归模型，进而得出较优的设计方案。

转运溜槽；尺寸几何；流动模型

转运溜槽是在散装物料输送系统中起导流和改向作用的一种设备，溜槽设计是需要考虑很多因素的复杂过程，不仅要考虑溜槽磨损情况，还要考虑物料特性和进入下个设备的角度。传统的溜槽设计，通常都是设计师凭借多年的设计经验进行的[1-3]。但在实际应用中，经常出现溜槽堵塞、灰尘飞扬及受料处因冲击破坏严重等问题，这都是因为溜槽设计不合理所造成的[4-7]。为了正确选择转运溜槽的几何尺寸，在满足溜槽设计准则的条件下，采用回归正交设计的方法，对其进行试验设计，并建立回归模型；基于Matlab程序[8]，实现转运溜槽的优化设计。

1 转运溜槽中的物料运动

溜槽自身和受料带的磨损情况与物料运动状态有关，因此，有必要对转运溜槽内的物料运动进行详细分析。

1.1 物料单元体流动模型

为了分析方便，对物料单元体的运动提出以下三点假设[9]：在流动过程中，物料分布是连续均匀的；物料之间不存在相互作用；忽略溜槽内的空气阻力。

选取沿单元体法线方向为坐标轴N，切线方向为坐标轴S，则单元体所受的力包括离心力Δman、重力Δmg、摩擦力FD、惯性力Δmat及溜槽面支反力FN，单元体受力示意图如图1所示。

据法向与切向的力平衡关系，可得出

Δmgcosθ-Δmat-μE(Δmgsinθ+Δman)=0，

(1)

简化后为

at+μEan+g(μEsinθ-cosθ)=0，

(2)

式中：Δm为单元体的质量，kg；at为单元体的切向加速度，m/s2；an为单元体的法向加速度，m/s2；μE为物料与溜槽之间的等效摩擦系数；θ为基于垂直线的溜槽倾角，(°)。

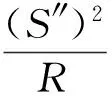
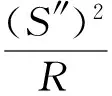
(3)

式中：R为单元体所在处溜槽的曲率半径，m；S为溜槽入口处到单元体处的距离，m。

图1 单元体受力示意图Fig.1 Schematic diagram showing the force acting on cell body

1.2 等效摩擦系数

对于常用的矩形截面溜槽，物料所处溜槽截面周围的压力分布如图2所示。

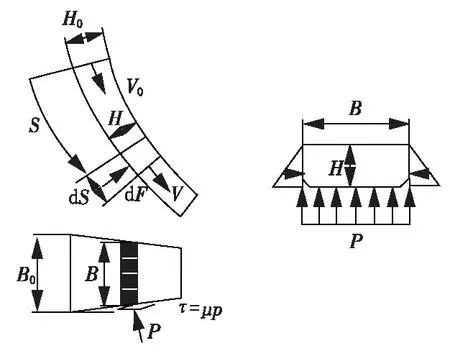
图2 变宽溜槽压力分布示意图

沿溜槽长向的单位长度总摩擦力为

F=μPB+μKVPH，

(4)

令F=μEPB，

联立式(3)、式(4)可得

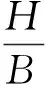
(5)

式中：μ为物料与衬板间的摩擦系数；P为溜槽底部均布压力，Pa/m；H为溜槽内料流层的高度，m；B为溜槽截面宽度，m；KV为溜槽底部横向压力与垂直压力之比，通常KV=0.4～0.6。

1.3 运动方程求解

对于矩形截面、曲率为常数的溜槽，式(3)的近似解为

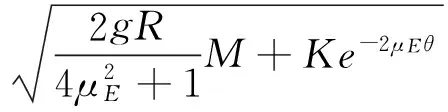
(6)

M=(1-2μ2E)sinθ+3μEcosθ。

对于V=V0，在θ=θ0处有

(7)

此时，M=(1-2μ2E)sinθ0+3μEcosθ0。

当θ0=θ且V=V0时，则有

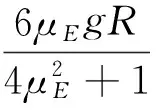
(8)

当式(3)中的R→∞时，圆弧段溜槽将变成直线段溜槽，则直线段溜槽中的物料流动速度为

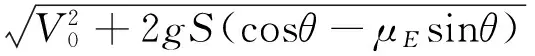
(9)

2 溜槽与输送带的磨损

溜槽磨损包括物料流动与溜槽表面接触引起的摩擦磨损和因物料垂直于受料带的分速度引起的撞击磨损，现就不同磨损情况进行分析。

2.1 溜槽摩擦磨损因子

对于图1的矩形截面、等曲率溜槽，其底面的摩擦磨损因子可以采用式(10)表示，

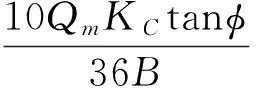
(10)

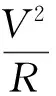
(11)

Qm=3 600Aβυρ，

(12)

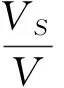
式中：WC为摩擦磨损因子，N/(m·s)；Qm为物料流量，t/h；φ为物料与溜槽表面间的摩擦角，(°)；NWR为无量纲磨损数；V为物料平均流速，m/s；VS为散装物料在溜槽底面滑动速度,m/s；A为溜槽的截面积，m2；β为溜槽截面装满系数，煤取0.3～0.4，ρ为散料密度，t/m3。

与溜槽底面的磨损相比，物料与溜槽侧面的磨损要小得多，磨损量从物料表面处的零达到溜槽底面处的最大值。假设溜槽侧面所受压力沿侧面从物料表面到底部线性增加，则溜槽侧面所受的平均磨损量为

(13)

式中：WCSW为溜槽侧面所受平均磨损量，N/(m·s)。

2.2 受料带的磨损

物料从溜槽终端到达受料带时的速度垂直分量及物料密度影响受料带的撞击磨损，此时物料速度的水平分量与带速之间的相对滑动速度与磨损量也有关。喂入溜槽受力示意图如图3所示。

图3 喂入溜槽受力示意图 Fig.3 Diagram showing the force to which the feed chute is subjected

Wa=1 000μbρV2evVS，

(14)

VS=Vb-Vex，

(15)

式中：Wa为受料带的磨损量，N/(m·s)；μb为散料与输送带间的摩擦系数；VS为物料速度的水平分量与带速之间的相对滑动速度，m/s；Vb为受料带的运动速度，m/s；Vex、Vev分别为溜槽终端出口速度的水平分量和垂直分量，m/s。

3 转运溜槽回归正交试验设计

假设输送系统的输送能力为5 000 t/h，入料口物料的垂直速度V1=5.25 m/s，散料密度ρ=0.80 t/m3，受料带速度Vb=5.85 m/s，物料与溜槽之间的等效摩擦系数μE=0.5。根据物料顺利流动的条件，溜槽出口倾角应满足φ≥arctan(μE)+5°=31.57°。

利用回归正交设计方法[10-11]，首先确定考察的指标为NWR，影响因素为R、溜槽入口角度为θ、转运高度为Ht、溜槽倾角φ。每个因素的因素水平表见表1。

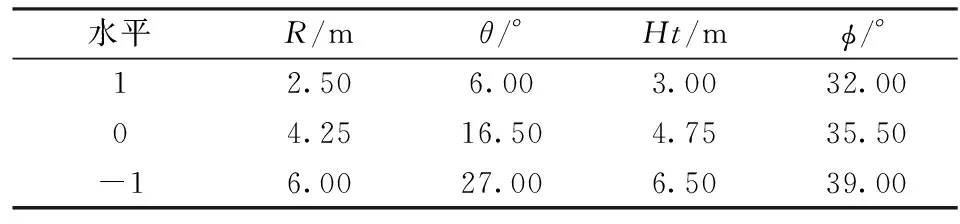
表1 因素水平表

其次，根据因素个数，选取正交设计表进行试验设计。圆弧段和直线段组成的溜槽试验方案和试验结果通过MATLAB编程计算获得，具体见表2，回归分析结果如图4所示。

表2 试验方案和结果

图4 回归分析结果

由图4得出的回归方程为y=35-1.12x1-0.15x2-0.02x3-0.14x4，因素主次顺序为R、θ、φ、Ht。由于偏回归系数为负数，故应该选择因素变化范围内的较大值，即R=6 m、θ=27°、Ht=6.5 m、φ=39°，在此情况下y=19.03。回归分析结果与表2结果基本相符，说明第一个试验方案比较合理。

4 结语

针对正确选择转运溜槽几何尺寸的问题，利用回归正交试验设计方法，建立无量纲磨损数与影响因素之间的回归模型，通过回归分析得出较好的试验方案。对于圆弧段加直线段的组合溜槽，几何尺寸可以选择圆弧半径为6m、溜槽入口角度为27°、溜槽总高度为6.5 m、溜槽出口角度为39°。

[1] KATTERFELD A, GROGER T, MINKIN A. Discrete Element Simulation of Transfer Stations and their Verification[J]. Bulk Solids & Powder, 2007, 2 (2):137-143.

[2] WENSRICH C M. Evolutionary optimization in chute design [J]. Powder Technology,2003(138):118-123.

[3] CEPAR T G, KETTERFELD A. Application of the discrete element method in materials handling [J]. Bulk Solids Handling, 2007, 27(1):17-22.

[4] MATON A E. Transfer Station Design[J].Bulk Solid Handling,2009,29(1)：30-34.

[5] VAN AARDE M N. The optimization of transfer chutes in the bulk materials industry[D].2009 Potchefstroom, The North-West University:30-37.

[6] KESSLER F.DEM-Simulation of conveyor transfer chutes[J].FME Transaciton,2009(37):185-192.

[7] 乔清山.煤矿溜槽的设计[J].煤矿机械，2015，36(5)：165-167.

[8] 褚洪生，杜增吉，阎金华. MATLAB7.2优化设计实例指导教程[M].北京：机械工业出版社，2007.

[9] 朴香兰.带式输送机转载溜槽试验设计研究[J].中国矿业,2014,23(8)：152-156 .

[10] 李云雁，胡传荣.试验设计与数据处理[M].北京：化学工业出版社，2008.

[11] 邱轶兵.试验设计与数据处理[M].合肥：中国科学技术大学出版社，2008.

MATLAB-based transfer chute design

PIAO Xiang-lan

(Institute of Engineering, Yanbian University,Yanji, Jilin 133002, China)

Acting as a connection unit in material handling link, transfer chute performs the guiding and splitting functions in material conveyance. For ensuring the selection of more precise geometric diameters of the transfer chute and non-obstructive material flow, a kinematic analysis is made of the material flow in chute and based on result of the analysis, the material flow model is developed. Following that regression modeling of transfer chute is made based on the result of test obtained using regression orthogonal design method and MATLAB scripts.

1001-3571(2016)05-0077-03

TD402

A

Keywordstransfer chute; geometric parameter; flow model

2016-08-30

10.16447/j.cnki.cpt.2016.05.021

朴香兰(1964—)，女，朝鲜族，吉林省龙井市人，教授，博士，从事机械现代设计理论与方法方面的教学与研究工作。

E-mail： piaoxl@ybu.edu.cn Tel：18686334080

朴香兰. 基于MATLAB的转运溜槽设计[J]. 选煤技术，2016(5)：77-79，83.