西南印度洋洋中脊(SWIR)热液A区的超慢速区岩浆活动的热模拟*

卞 龙， 张 健†， 阮爱国

(1 中国科学院计算地球动力学重点实验室， 北京 100049； 2 中国科学院大学地球科学学院， 北京 100049；3 国家海洋局第二海洋研究所， 杭州 310012； 4 国家海洋局海底科学重点实验室， 杭州 310012)(2016年3月10日收稿； 2016年4月1日收修改稿)

洋中脊是火山活动频繁、岩浆上涌和新洋壳形成的巨型活动构造带，是全球地质演化中最重要的构造单元之一.对洋中脊的调查研究有助于提高对地球深部构造、地球内部动力状态、岩浆起源与演化以及海底热液成矿理论等科学问题的认识.超慢速扩张洋脊一般是指全扩张速率小于20 mm·a-1的大洋中脊，西南印度洋洋中脊 (SWIR) 扩张速率仅为14～16 mm·a-1，是研究超慢速扩张洋脊的理想区域[1-4].但由于受其偏僻地理位置的约束，与大西洋中脊(MAR)、东太平洋海隆(EPR)相比，SWIR至今仍是全球洋中脊调查研究和取得认识较少的地区之一.中国在2005年第一次实施环球科考航次，并在随后的洋中脊科考调查中，发现了位于超慢速扩张洋中脊的第一个海底热液活动区[5].2010年，中国大洋环球21航次在该热液区的A区 (49°39′E) 开展三维地震深部探测，获得其地壳和上地幔深部的速度结构[6]，并在第27洋段发现大尺度低速区[7-10]，认为可能是岩浆房或熔融体的存在造成的[11].

洋中脊扩张轴下的岩浆房(axial magma chamber, AMC)是洋中脊研究的重点[8,10,12].数值热模拟可以为扩张轴下的岩浆活动提供更为精确的量化结果，为深部岩石圈的结构研究提供更为可信的科学依据[13-16].本文根据SWIR的构造特点，结合地震反演结果，对低速异常区进行热模拟研究.通过修正热导率随温度变化对热结构影响模型，利用反演手段推测研究区莫霍面温度，最后讨论研究区的热结构及其岩浆房特征和演化过程.

1 区域地质背景

SWIR是非洲板块和南极洲板块的主要边界，其西端起于大西洋洋中脊(MAR)与美洲-南极洲洋中脊(AAR)交点，即布韦三联点(BTJ, 55°S, 0°40′E)，以近西南—东北走向延伸约8 000 km，与中印度洋洋中脊(CIR)和东南印度洋洋中脊(SEIR)相交于罗德里格斯三联点(RTJ, 25°30′S, 70°E).SWIR具有超慢的扩张速率和斜向扩张的特征：全扩张速率仅为14～16 mm·a-1，而扩张方向从N18°E变化到N0°E.SWIR中央裂谷区域构造复杂，轴部峡谷水深超过5 000 m，岩浆作用聚集区与非岩浆作用扩张带的相互作用形成多样化的海底地形[17].如图1(a)所示，SWIR被一系列近南北向转换断层切割.以转换断层Andrew Bain (AB) 为界，分为东西两部分，向西依次经过Du Toit (DT)，Shaka (SH)，Islas Orcadas (IO)，Bouvet (BO) 一直到BTJ转换断层；向东依次经过Marion (M)，Eric Simpson (ES)，Discovery II (DII)，Indomed (IN)，Gallieni (GA)，Atlantis (AII)，Melville (MEL) 一直到RTJ转换断层[18-19].沿SWIR的大断裂带，可见辉长岩和岩浆喷溢形成的玄武岩[20-21].断层附近有大量蛇纹石化橄榄岩出露，地壳厚度薄，岩浆供给少且不连续，这是超慢速扩张脊的重要特点.在SWIR西段的9°～16°E之间，洋脊高角度斜交于区域扩张方向；在16°～24°E之间，洋脊由一系列非转换不连续断层段组成，且近似垂直于扩张方向.而SWIR东段的63.6°～64.3°E之间，扩张速率相对较慢，使得洋壳增生的不对称性和空间变化更加明显[22,17].

2010年，中国大洋21航次第6航段对A区开展了三维地震深部探测[5-11]，探测区域如图1(b)所示.A区热液喷口位于转换断层IN和GA之间的第28洋脊段上，IN-GA段是SWIR上水深最浅的区域之一，此段相比于其东西两侧的洋中脊段表现为明显的地形隆起[23].A区是一个近东西走向的狭长裂谷，其南北两侧陡崖高上千米，其东侧是一个尚未发现热液活动的玄武岩高地.A区与玄武岩高地相邻属同一洋脊段，却出现近2 km的地形高差，这样的地形差异在SWIR上普遍存在，说明洋中脊下的岩浆并不是连续分布的.最新的三维地震资料显示，在玄武岩高地下存在低速异常体，其很可能存在岩浆房，且热液喷口的通道很可能就是一条从玄武岩高地下面通向热液喷口的水平通道[8-9].

图1 区域地质背景图[8-9]Fig 1 The regional geological map

2 数值模拟

首先，我们选取三维地震探测区域中26号台站下的区域，结合其他的地球物理资料，使用有限元方法构建基本计算模型.考虑岩浆房内岩浆的流动，分别计算岩浆房底部无热源和存在热点持续供热的情况，实现对研究区的初步数值热模拟.

2.1 基本模型及参数

图2(a)为SWIR地震速度剖面[8-9].研究区洋壳厚度约为10 km，莫霍面深约为12 km.超慢速洋中脊的地壳沿中脊平均厚5～6 km，但在火山区却厚达8 km.研究区洋脊段岩浆集中，有火山或非活动喷口，地壳较厚；非转换不连续带(NTD)和中脊裂谷地壳薄，存在热液活动喷口.厚地壳与薄地壳相间，呈水平放置的一串葫芦.在27洋脊段(Seg.27)地震波速度等值线分别上升和降低，位于图2(a)中x方向约100 km处可见大尺度低速区，其高度约为4 km，即图2中虚线方框区域.

图2(b)为基于速度结构的热模拟模型.该模型长15 km，深14 km，由5层组成，从浅到深分别为：海水层2 km；洋壳层2A和2B厚度～2 km，2A层的边界起伏较大；洋壳层3厚度～8 km；上地幔层厚度～2 km，莫霍面略微抬升.考虑到地质演化过程中压实作用会在纵向上产生一定程度的收缩以及冷却过程中岩浆房规模的减小，我们假设古岩浆房由幔源岩浆上侵形成，位于下地壳(洋壳层3)的截面积为3 km(EW)×5 km(Z)的锥体.坐标系原点位于模型左上角，用三角形网格对模型剖分，共计3 871个网格单元.模型上边界为海水层，海底温度固定为8 ℃；左右边界均为自由边界；设岩浆房初始温度取1 200 ℃，模型其余部分的初始温度为模型达到稳态时的温度场，温度随深度呈分段线性变化.根据洋中脊岩性分布和岩浆性质给出模型的热力学参数，包括热导率、生热率、密度和比热容等，见表1.

2.2 计算方法

整个模型组成流固传热耦合场，满足下列方程组：

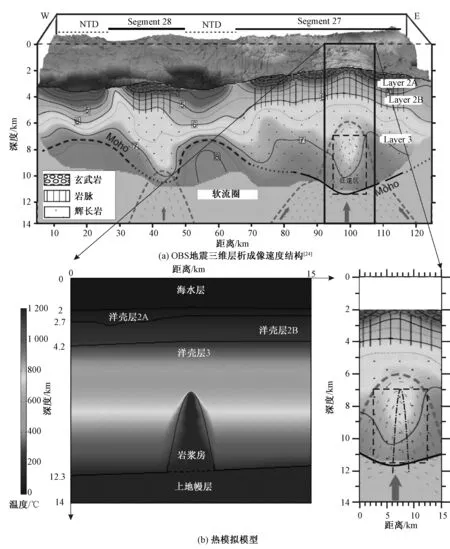
图2 研究区基本模型Fig 2 Basic model of the research area

热导率/(W·m-1·K-1)密度/(kg·m-3)比热容/(J·kg-1·K-1)生热率/(μW·m-3)海水层0.5410314200-洋壳层2A2.725509000.02洋壳层2B327709000.02洋壳层32.328309000.02岩浆房3.3265012000.033上地幔层3.3319010000.033

(1)

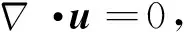
(2)

(3)

其中，洋壳部分满足瞬态二维热传递方程(式(1))；定义岩浆房内的岩浆为不可压缩的牛顿流体，且符合布辛涅司克近似，满足连续方程((式)2)和纳维斯托克斯方程((式)3).ρ、c和k分别为岩层的密度、比热和热导率；T为温度；t为时间；u表示岩浆上涌速度；P表示压力；g为重力加速度；Q为岩石放射性产热率.

Δρ表示由温度变化引起的密度差，定义为

Δρ=ρ0αΔT，

(4)

其中，ρ0表示初始温度时岩浆的密度，α为热扩散系数，本文中取α=3×10-5℃-1，ΔT为温度变化量.

η表示随温度变化的岩浆黏度，黏度随着岩浆房的逐渐冷却而增大，当黏度趋于无穷大时岩浆凝固为岩石[28].η的展开式为

(5)

其中，R为气体常数；T为温度；E为活化能；η0和Tb表示上地幔的背景黏度和温度，本文中取E=120 kJ·mol-1，η0=1×1021Pa·s，Tb=1 350 ℃[28].

我们采用等效比热法来处理岩浆房内岩浆固结相变时释放的潜热[15]，公式[29]如下

(6)

其中，Ceff为等效热容，Cs为凝固后的固体热容，Cl为凝固前的液体热容，Ts和Tl分别为固相线和液相线温度，Lf为熔融潜热.本文中取Cs=900 J·kg-1·K-1；Cl=1 200 J·kg-1·K-1；Ts=1 100 ℃；Tl=1 250 ℃；Lf=400 KJ·kg-1 [30].

设无热源模型的底边界(莫霍面)为无热流边界，此时模型仅存在岩石以及岩浆房内部放热；设热点持续供热模型的底边界(莫霍面)为60～80 mW·m-2(岩浆房两侧底边界为60 mW·m-2，岩浆房底边界为80 mW·m-2) 的热流边界[31].

3 结果与讨论

3.1 岩浆房底部热源的影响

热模拟计算表明，岩浆房持续供热时间约为2.3 Ma.观察岩浆房顶部正上方1 km(坐标7.5 km，6 km)处的温度变化(图3(a))，地壳温度经岩浆房加热后迅速升高，经过约0.1 Ma由480 ℃左右迅速升至534 ℃.随着岩浆房的逐渐冷却，地壳温度迅速降低，约1 Ma后温度下降至487 ℃，之后温度下降速率迅速减小，再经过1 Ma仅下降4 ℃，最后该深度地层在约2 Ma后基本达到483 ℃的稳态.

岩浆房顶部正上方1 km(坐标7.5 km，6 km)处的温度变化表明岩浆房持续供热时间明显增长，约为10 Ma，如图3(b)所示.地壳温度经岩浆房加热后迅速升高，经过0.1～0.3 Ma，岩石圈迅速升温，当温度到达峰值后岩浆房逐渐冷却，地壳温度也逐渐降低，约2 Ma后温度下降速率变小，约10 Ma后该处地壳基本达到115 ℃的稳态.

为了更直观地对比以上两种模型的模拟结果，我们分别对其温度值进行归一化处理，公式如下

T*=(T-Tmin)/(Tmax-Tmin)，

(7)

其中，T为模拟计算所得的每个时间点上的温度，Tmax为温度的最大值，Tmin为温度的最小值，T*表示归一化处理后的温度.

将归一化处理后的曲线绘制到同一坐系上，如图3(c)，其中实线表示无热源模型结果，虚线表示存在热点持续供热的结果.对比两条曲线的斜率可以明显看出，存在热点供热时洋壳的加热和冷却速度都更加平缓.当洋壳层底部没有持续热供应时，岩浆房在1 Ma之内迅速冷却，岩浆房持续存在时间在1.5～2.3 Ma，表明现今热液活动的热源不是无热源的古岩浆房提供的；显然，当洋壳层底部存在热点持续供热时，岩浆房冷却更缓慢且持续时间更久，约8～10 Ma.热点持续供热的岩浆房更有可能为现今的海底热液活动提供热源.

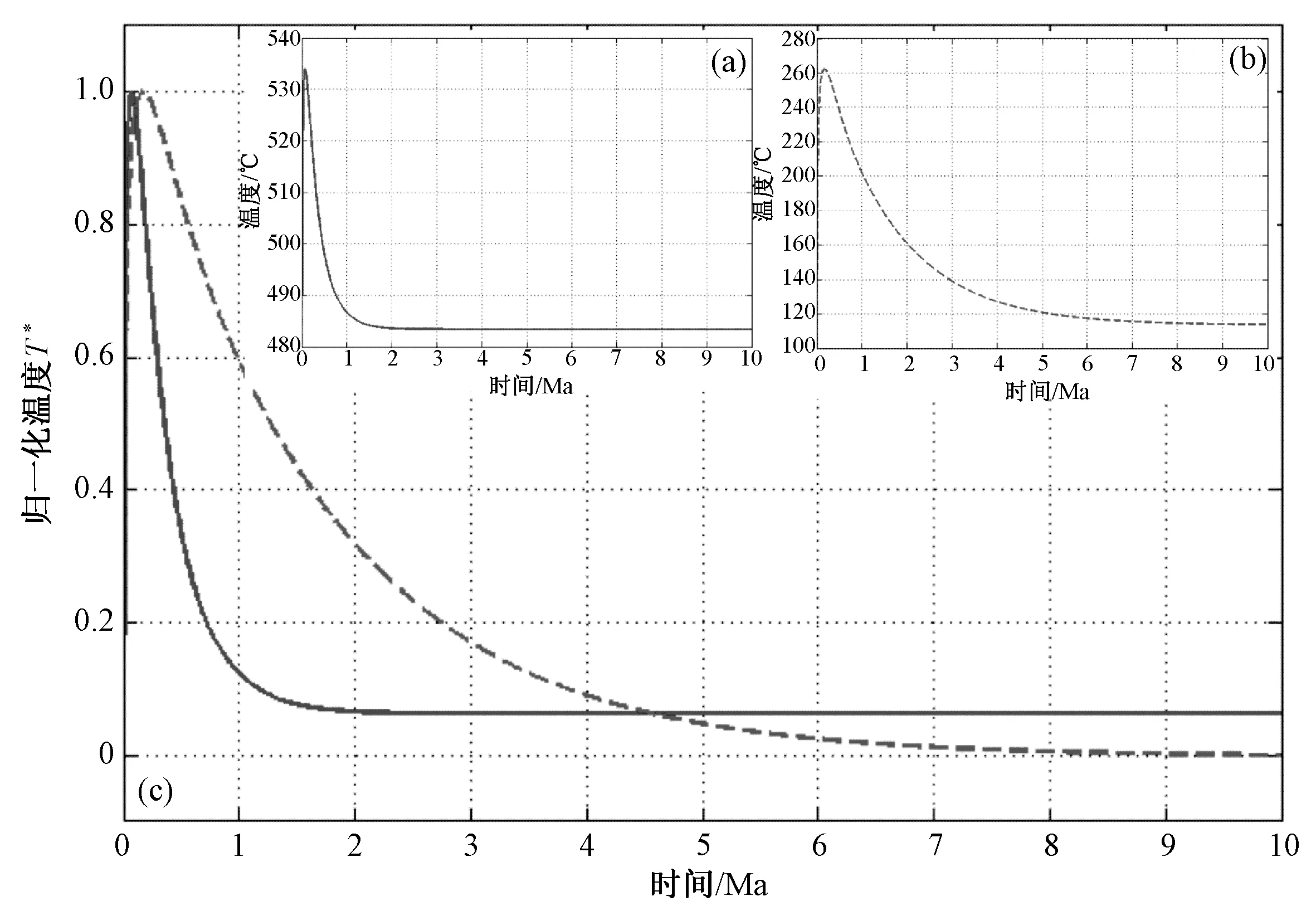
(a) 岩浆房底部无热源模型; (b) 岩浆房底部存在热点持续供热模型; (c) 归一化处理后两种模型对比图.图3 岩浆房顶部正上方1 km处温度随时间变化曲线Fig.3 Temperature variation curve 1 km above the roof of magma chamber

但对比两种模型的计算结果会发现：无热源模型冷却迅速，达到稳态时洋壳温度高，莫霍面温度达到1 200 ℃左右；而热点持续供热模型虽冷却时间长，但达到稳态时洋壳温度偏低，莫霍面温度仅为400 ℃左右，这与西南印度洋莫霍面温度600～1 200 ℃的范围不符.这种结果可能由两种原因造成：1)初步热模拟模型中将热导率作为常数处理，而实际上热导率是随温度变化的，采用随温度变化的热导率可能会修正热模拟计算结果.2)SWIR热点热流可能远比80 mW·m-2要大.下面分别针对这两点做进一步分析.

3.2 热导率对温度的影响

随着温度升高“热降解”产生，岩石颗粒间距增大，接触热阻抗增大，热传导系数降低，即热导率与温度呈反相关系.在温度较低的情况下，热导率随温度升高逐渐减小，但当温度升高至1 200 ℃左右时，热导率不再随温度变化，而是基本保持不变，极端情况甚至发生逆转.热导率较小时，热的传播效率低，相同条件下比热导率较大时同一深度地层传出的热量少，导致该地层温度更高.

选取与洋壳层2成分相同的基性岩层做单层水平模型，深度为40 km.设基性岩常数热导率为2.534 W·m-1·K-1，如图4(a)中实线所示.鉴于Zoth和Haenel[32]提出的热导率导数型经验公式

(8)

应用最为广泛，基性岩和超基性岩变化热导率均采取以上模式，其中a、b采用实验室统计拟合结果[32-35]，基性岩a=1.18，b=474，超基性岩a=0.73，b=1 293.图4(a)中的虚线和点线分别表示基性岩和超基性岩随温度变化的热导率，超基性岩热导率在此仅起对比作用，不参与模型计算.模型顶端边界固定为0 ℃，首先给底边界加30 mW·m-2的热流，分别计算常数热导率和变化热导率条件下达到稳态时的温度结构.计算结果如图4(b)中的x曲线和p曲线所示，二者在40 km处分别达到473 ℃和611 ℃.然后在模型底部使用35 mW·m-2加热20 Ma，二者在20 Ma后的温度结构分别为图4(b)中的曲线y和q，温度分别升高到552.42 ℃和732.76 ℃，升高幅度分别为79.42 ℃和121.76 ℃.由图4可见，采用随温度变化的热导率时，地层的温度比采用常数热导率模拟的结果更高，随着深度增加，地层温度的增加量更大，深部更加容易积聚热量.在数值热模拟中，使用随温度变化的热导率对计算结果影响较大.

3.3 热点热流与莫霍面温度

在基本模型的基础上修改洋壳层的热导率，设定不同的热导率模型，计算莫霍面温度，并通过对比西南印度洋洋壳内地热资料，利用反演方法对模型系数加以约束，进而讨论不同热导率模型系数与实验室计算的热导率系数之间的关系.最后，在温度对热导率产生影响的条件下约束热点热流，并探讨莫霍面温度.

对基本模型中的洋壳层2，采用公式(3)的倒数型热导率模型，其中a、b的取值范围为0≤a≤1.5，0≤b≤1 500.

图4 温度对热导率的影响Fig.4 Influences of temperature on thermal conductivity

反演方法为：选取热点热流范围从30～300 mW·m-2，步长为10 mW·m-2；对于每个热流值分别滑动选取不同的a、b，其中a的范围0～1.5，步长为0.1，b的范围0～1 500，步长为50；正演计算，求得不同热流条件下，不同a、b系数对应的莫霍面温度值；以莫霍面温度范围600～1 200 ℃作为约束，筛选符合条件的a、b系数.

Zoth和Haenel[32]统计了岩盐和石灰岩等沉积岩，酸性岩、基性岩和超基性岩等岩浆岩，以及变质岩在不同温度条件下的热导率，并根据式(3)得到不同岩石对应的模型系数a、b值.图5显示了这些值，○、□、△、×、+、*分别表示超基性岩、石灰岩、变质岩、酸性岩、基性岩、酸性岩的实验室a、b系数.超基性岩以外的岩石 (图符B-F)a、b值可近似拟合为一条直线，表达式为b=-573a+1 160，如图5中的实线所示.超基性岩 (图符A) 这一特例可能与其深部特征有关.

图5 岩石热导率系数的实验室统计分布Fig.5 Laboratory statistical distribution of thermal conductivity coefficient of rock

将反演计算结果与实验室统计结果进行对比，反演模拟结果表明，符合莫霍面温度范围约束的a、b值分布也是线性的.实验室结果和模拟结果分布特点一致，且二者的线性拟合直线存在相关性.理论上讲，与实验室统计分布最为接近、相关性最高的反演结果对应的热点热流最为接近实际情况.图6(a)—图6(f)为不同热点热流对应的反演计算结果，分别对应热流为110、150、190、220、240和280 mW·m-2的热流边界条件.随着热流值的增大，反演的a、b系数曲线斜率逐渐增大，与实验室统计结果的相关性逐渐增大，当热流为190 mW·m-2时与实验室统计结果最为接近，如图6(c)所示.随后随着热流值增大，反演结果的斜率与相关性都逐渐减小.所以推测研究区热点热流值约为190 mW·m-2，与之对应的莫霍面温度约为910 ℃.

3.4 研究区热结构

使用随温度变化的热导率以及190 mW·m-2的热点热流条件，改进模型并做数值热模拟，得到研究区的热结构及岩浆房特征，并推测其演化过程.图7(a)为研究区初始状态等温线图，莫霍面存在约190 mW·m-2的热点热流对岩浆房底部持续加热，造成岩浆房内部岩浆密度随温度变化产生自然对流，岩浆上涌，此时岩浆流速度最大值约为12 mm·a-1.在随后的0.3 Ma里洋壳层受岩浆房加热影响，温度迅速上升，图7(b)为研究区0.3 Ma时的等温线图，此时岩浆房内最高温度达到1 250 ℃左右，洋壳温度也达到峰值.当温度达到峰值后，岩浆房内的岩浆流速度最大值逐渐变小，岩浆开始冷却凝固，岩浆房和洋壳的温度也随之降低，岩浆房规模逐渐缩小直至消失，图7(c)为研究区2 Ma时的等温线图.计算表明，大约8～10 Ma后岩浆房消失，岩浆流速减小至0 mm·a-1，洋壳层经历了迅速加热和逐渐冷却的过程后达到稳态，此时莫霍面温度约为910 ℃，如等温线图7(d)所示.假若地层与温度剖面之间存在很好的对应关系，那么在地壳冷却过程中，洋壳层2和洋壳层3将会分别增厚和减薄.如果模型横向展布更宽，温度剖面与地层剖面会吻合得更好.因此，我们推测古岩浆房内岩浆在沿断裂移动过程中可能产生热异常，导致生成新的岩浆房，形成现今的熔融低速区.现今的热液活动，一种可能是古岩浆房中的岩浆沿断裂溢出地表形成，另一种可能是新岩浆房对其供热形成，如图8所示.

图6 不同地幔热流对应的a、b系数反演结果与实验室统计结果对比Fig.6 Comparison of a and b coefficients under different mantle heat fluxes betweeninversion results and laboratory statistical results

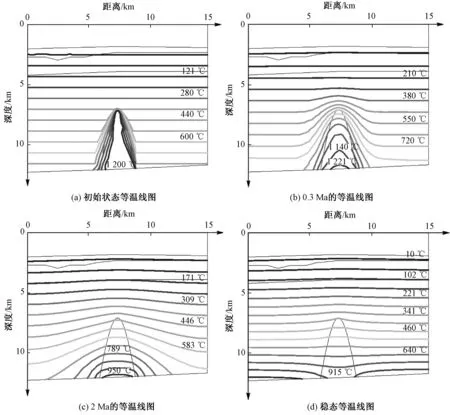
图7 研究区热结构的时间演化图Fig.7 Evolution of thermal structure in the research area

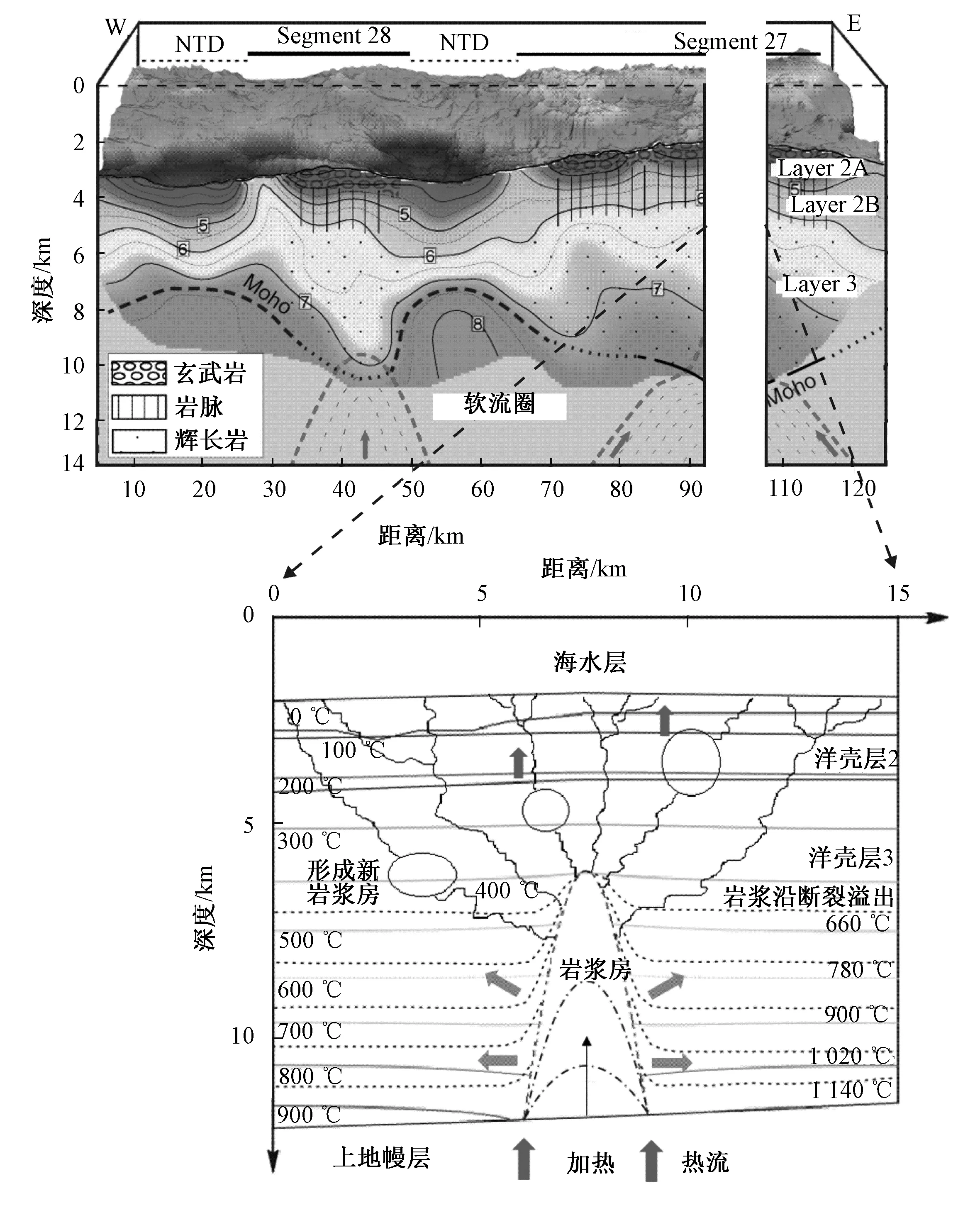
图8 研究区热结构Fig.8 Thermal structure of the research area

4 主要结论

1)在数值热模拟中，热导率对温度的影响不可忽视.相比使用常数热导率进行热模拟，使用随温度变化的热导率计算结果温度更高，也更加接近实际情况.

2)以实验室统计参数a、b分布为基本依据，利用莫霍面温度范围作为约束，反演计算热导率系数a、b，使其分布与实验室统计结果一致，得到最接近实际的情况，以此推测研究区热点热流约为190 mW·m-2，莫霍面温度约为910 ℃.

3)当洋壳层底部没有持续热供应时，岩浆房持续时间仅为1.5～2.3 Ma，不能为现今的岩浆活动提供热源.当存在热点持续供热时，岩浆房持续时间约8～10 Ma.猜测热点供热使岩浆在沿断裂移动过程中产生热异常，或产生新的岩浆房，岩浆沿断裂或通过岩浆房溢出地表与海水作用而形成热液活动.更进一步的结论还需更多后续研究.