加强发散思维训练提高创造思维能力

四川省眉山市东坡区柳圣乡初级中学(620035)

时兴中●



加强发散思维训练提高创造思维能力

四川省眉山市东坡区柳圣乡初级中学(620035)

时兴中●

创造性思维的过程是一种身心的综合性劳动，因而单是掌握方法是不能解决问题的.这里既需要具备发现问题的自觉性，又不能缺少信息的积累.本文重点例举典型实例从方法论高度开阔解题思路，每一个题目都从不同角度不同方法获取答案，这不仅知识积累更重要是掌握正确的思想方法.

复称法；减码法；累积法；扩缩法；液压法；设计方案

本文举例谈谈在解题时，发散思维训练过程中培养创造思维.

一、实验室中测量质量的仪器是天平.天平的实质是等臂杠杆，只有两边的质量相等时杠杆才能平衡.因此可用已知质量的砝码测出未知质量物体的质量.但是如果某一天平由于使用不当和部分破损，致使等臂天平变为不等臂，又将如何用这样的非常天平测量物体的质量呢？有以下几种方法可供大家实践.

方法一 复称法

第一步，将待测物体mx，放入左盘中，右盘中加入质量为m1的砝码，天平再次平衡，根据杠杆平衡条件：

mxgL1=m1gL2①

第二步，将待测物体mx放入右盘中，左盘中加入质量为m2的砝码，天平再次平衡，根据杠杆平衡条件：

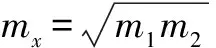
方法二 减码法

设物体质量为mx，取m>mx的物体放入左盘，右盘放砝码至平衡.左盘物体m不动，再将mx放入右盘，从右盘取出适量的砝码Δm使之平衡，则mx=Δm.

第一步m放在左盘，m1放在右盘，得：

mgL1=m1gL2①

第二步 左盘m不动，再将mx放在右盘，从右盘取出Δm使天平平衡得：mgL1=[(m1g+mxg)-Δm]L2②，由①与②得m1gL2=[m1g+mxg-Δmg)]L2,mx=Δm

方法三 替换复称法

第一步：在左盘放上砝码m1，右盘放入砝码m2，当杠杆平衡时：m1gL1=m2gL2,则L1/L2=m2/m1①

第二步：再将待测物体mx放入左盘中，右盘中加入质量为m3的砝码，天平平衡，此时mxgL1=m3gL2,则L1/L2=m3/mx②.由①②两式即可求出：mx=m1m3/m2

方法四 干沙替代法

左盘放物体，右盘加干沙，使天平平衡，拿掉左盘被称物体，换上砝码重新使天平平衡(右盘的沙子不能动).这时砝码所示的值即为待测物体的质量.

方法五 累积法

把适量的砝码m2放在天平的左盘内，再在天平的右盘中加砝码m1使天平平衡，由杠杆的平衡条件得：

m2gL2=m1gL1①

再将待测物体mx放在左盘内，在右盘内再加砝码m3使天平重新恢复平衡，则：(m2+mx)gL2=(m1+m3)gL1②

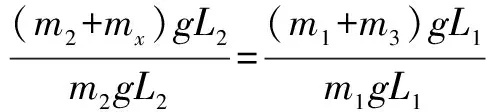
二、把水池中小船上所载的石块投入水中，池中水面为什么要降低

石块被投入水中后，将侵占原来被水占据的空间而使池中水面上升，但船却因载重量减小而向上浮起，从而使池中水面下降.这里既有使水面上升的因素，又有使水面下降的因素.因此，对这个问题必须作仔细的分析，才能得到正确的答案.

方法一 常规思维方法

先分析当石块在船上时的情况.

设水对船的浮力为F浮，被船排开水的体积为V排，则

式中V排-V排′表示把石块投入水中后船减少的排水体积；V石等于投入水中的石块排开水的体积.两者比较，投入水中的石块排开水的体积不能补偿船减少的排水体积.总的排水体积减小了，所以，水面要下降.

方法二 扩缩法

常规解法过程严谨，但较为繁琐.现介绍一种“扩缩”解法，采用变换物质密度的方法，具有简洁、直观的优点，使解题过程大为简化，收到出奇制胜的效果.

先扩——先假设石块质量不变体积膨胀，使其密度变换成与水密度相同，由于船和石块总质量未变，因此池中水面高度保持不变，然后把膨胀后的石块投入水中，它将处于悬浮状态，这时水分别支持船和石块.

后缩——接着令石块收缩回原来的体积V石′，显然石块排水的体积变小，V石=m石/ρ水,∴V石

方法三 液体压强法

如图1，水池底受到压力F1=h1ρ水g·S1，石块抛出沉池底，如图2，这时池底受到压力F2=h2ρ水g·S2+(m石g-f浮)S2′.因水池底受力不变F1=F2，S1≈S2，所以h2

G632

B

1008-0333(2016)23-0054-01