抓住运动规律,巧解动点问题
江苏省射阳县实验初级中学(224300)
李立松●
抓住运动规律,巧解动点问题
江苏省射阳县实验初级中学(224300)
李立松●
图形中的动点问题是近年来中考数学的热门考点之一,这种题型结合多方面的知识,难度较高.学生们遇到此类问题往往找不到解题的切入口,因此,归纳常见动点问题的常规解法具有重要的意义,这有利于提高学生的思维能力,帮助学生脱离“歧路”,寻找到行之有效的方法.动点问题常与其他章节的知识点结合考察,我将借助相关例题帮助学生理解思路.
一、点的运动产生的规律归纳题
在点的运动过程中寻找规律的题目实际上就是通过观察点的运动轨迹,从而归纳总结出一条规律,解这种题目要重点把握点在运动初期的规律,从最初的几个点入手,这样能使解题过程更加流畅.
例1 如图1在一个坐标系中,有一个等边三角形,它的顶点O与坐标原点O相互重合,一条边OP落在X轴所在的直线上,如果把这个等边三角形沿着X轴的正方向连续转动2014次,求最终点P的坐标.
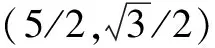
点拨 由最初的状态往后逐步探索,然后总结出规律,最终运用这个规律进行求解,这是处理这种类型题目的基本方法.
二、点的运动产生的最小长度问题
在点的运动过程中求最小长度,往往结合数形结合的思维方法,要充分利用图形本身的属性,如对称性等性质,如果学生能留心这些特殊的属性,那么往往能避免复杂的计算,给解题带来意想不到的帮助.
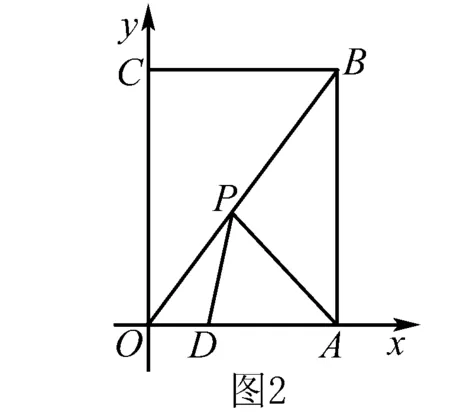
例2 在如图2所示的直角坐标系中,正方形AOCB的边长为12,P点在对角线BO上面运动,D点在边AO上面,它的坐标为(5,0),连接PD,AP,试求线段PD,AP长度之和的最小值.
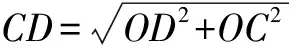
点拨 这道题目根据对称型把距离之和巧妙地转化成为求直角三角形的斜边长,简化了解题步骤,学生要留意这种巧妙的解法.
三、点的运动产生的函数最值题
点在函数图像上运动,往往能和其他的点构成不同的图形,与图形有关的量有时容易用函数关系表示,有时需要经过转化才能表示出来,学生要开阔思维,寻找最佳的转化方法,然后根据求解函数最值的方法便可求解.

例3 在如图3所示的坐标系中,二次函数y=x2-2x-3的顶点为D点,它的图像与y轴相交于C点,与X轴的负方向相交于A点,与X轴的正方向相交于B点,如果点G是其图像上的一点,它的横坐标为2,P点在抛物线上并且处于直线GA的下方,试求S△PGA的最大值以及此时P的坐标.

点拨 因为P点处于运动状态,直接求解AP边上的高十分困难,这道题中用分割三角形面积的方法避免了求高时的复杂计算,这种方法值得学生借鉴.
以上总结为三类常见的动点问题,正如解题过程所示,三类问题对应着三种基本数学思想分别为:归纳,数形结合以及函数思想,学生在训练动点问题时应该不断强化这三种思想,从而有效地提高解题能力.
G
B

