一道向量试题求解的三个视角

张同语

(安徽省五河第一中学，233300)



一道向量试题求解的三个视角

张同语

(安徽省五河第一中学，233300)

从近年来全国各地的高考试题看,高考对平面向量的考查难度在逐步加大,已从当初的对平面向量的基本概念、基本运算及几何意义等单一考查,逐步过渡到对平面向量与其他数学知识的交汇考查．但是无论平面向量的考查形式如何变化,我们只要从“坐标运算、非坐标运算、图形运算”这三个视角对题目所给信息进行审视,解题思路便会自然形成.下面以2016年浙江省理科数学第15题为例,以示说明．

一、试题呈现与立意分析

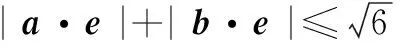
命题立意 本题以向量为载体融恒成立与最值问题,集向量、函数、不等式、三角等知识于一体,突出知识的交汇考查,立意深远,内涵丰富,思维要求高,解法灵活,兼顾形数,从中可以体会向量与代数和几何的紧密联系,具有很好的区分度．

二、解题探究与思路分析

视角1 坐标运算

思路分析 由题意,向量a、b、e的模已知,但是,它们的相对位置不固定,且单位向量e具有任意性,难以确定基底.因此,我们不妨固定已知向量a,以其为基础建立平面直角坐标系，利用向量的坐标运算解决问题．

解法1 以a为x轴的方向向量,建立平面直角坐标系,则a=(1,0),设b=(2cos θ,2sin θ),其中θ为a,b的夹角，则a·b=2cos θ,令e=(cos x,sin x)．

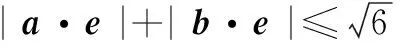
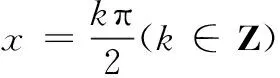
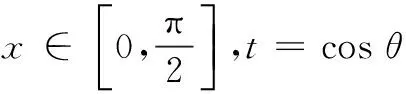
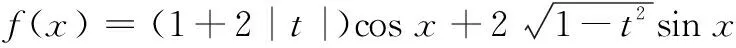
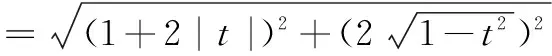
评注 通过建立平面直角坐标系,将向量代数化,综合运用主元分析,研究函数潜在的对称性质,体现了三角函数与向量的密切联系．

视角2 图形运算

思路分析 由平面向量数量积的几何意义知|a·e|,|b·e|分别表示向量a,b在e方向上投影所对应的有向线段的长度,故有数形结合的如下解法.

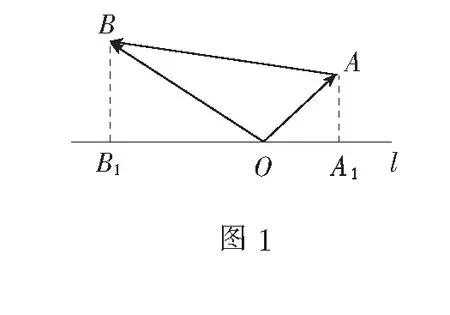
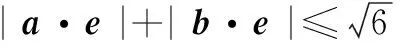
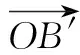
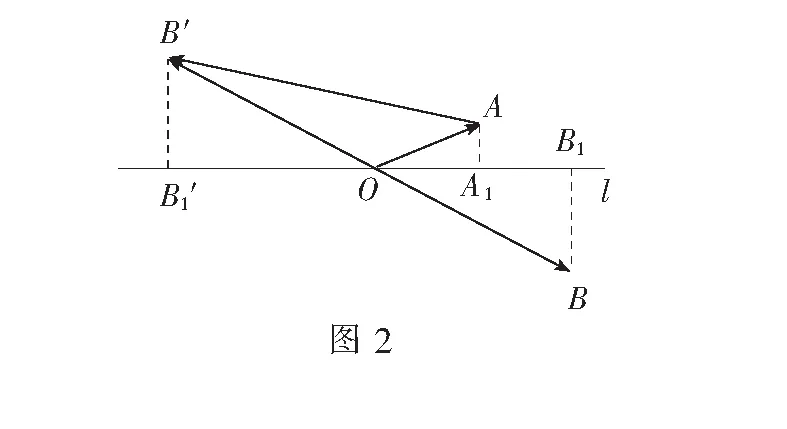
评注 向量的几何意义是向量中的精华,是实施数形结合的重要途径.虽然问题中的向量均在相对运动,但通过寻找问题的几何意义,构造相应的几何图形,根据图形运动变化中的几何量间的关系,进行运算变形,从而得到问题的直观解法．

视角3 非坐标运算

思路分析 因为平面向量的数量积是实数,实数的绝对值具有如下性质:|m±n|≤|m|+|n|,其中m、n∈R,利用此不等式可实现将数量积转化为向量模的不等式求解．或者利用向量的加法与减法运算遵循平行四边形法则,联想平行四边形的有关性质及向量的极化恒等式,可得如下解法.

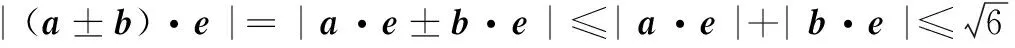
又|(a±b)·e|max=|a±b|,

又|a|=1,|b|=2,

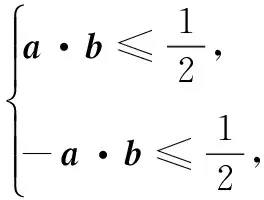
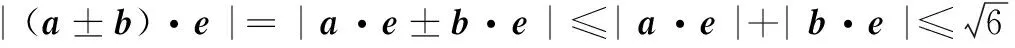
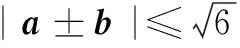
又∵(a+b)2+(a-b)2=2(a2+b2)=10，∴(a+b)2=(|a+b|)2≤6.

由向量极化恒等式,得

评注 解法2,解法3充分揭示了该试题的本源是向量数量积的几何意义与向量数量积对向量加法的分配律.当我们知道了该试题的本质,问题较为简洁的解法2、解法3 就水到渠成了．

三、解后反思

对于高考数学中有关平面向量的考题,灵活运用“坐标运算、图形运算、非坐标运算”这三个视角进行分析,结合解析几何、平面几何、函数、不等式等相关知识进行探究,问题便会迎刃而解．另外,从解题过程中,也让我们体会到数学基础知识、基本技能和基本思想对解题的重要性.关注解题后的反思,挖掘问题背后的知识本质,品味解题方法和思维的关键点,探究一题多解是我们走向以少胜多的高效学习之路．

设n=k时结论成立,即

0

根据函数f(x)在(0,1)内是增函数,可知

f(0)

所以,当n=k+1时,0