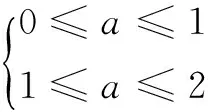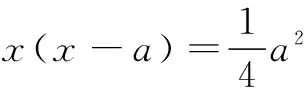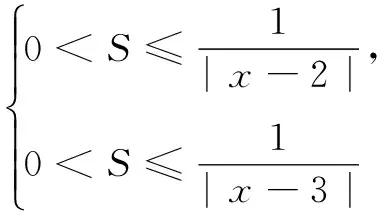局部含绝对值问题的教学策略

徐 琴

(江苏省昆山中学,215300)



局部含绝对值问题的教学策略

徐 琴

(江苏省昆山中学,215300)

函数y=|f(x)|和函数y=f(|x|)的问题,可转化为函数y=f(x)的相应问题解决,这一转换已为学生熟知．含有绝对值但不属于上述两种类型的函数问题,我们不妨称它为“局部含绝对值”的问题．例如下面的问题.

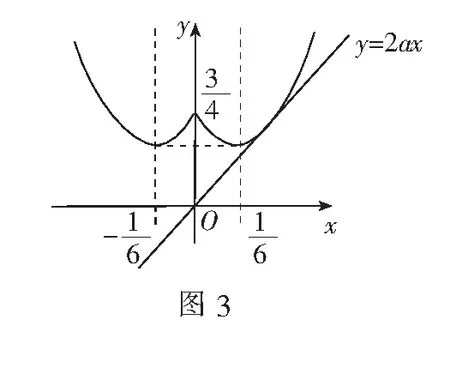
问题1 (2009年江苏高考题)设a是实数,函数f(x)=2x2+(x-a)|x-a|.(1)若f(0)≥1,求a的取值范围;(2)求f(x)的最小值;(3)设函数h(x)=f(x),x∈(a,+∞),直接写出(不需给出演算步骤)不等式h(x)≥1的解集．

当年该题得分率很低．又如下面的问题2、问题3，2015级高一学生两个学期四次(苏州全市及部分县市)统考卷中都出现了这类问题．那么,学生面对这类问题的困难在哪儿呢?在教学中应采取怎样的对策呢?

一、问题的症结

毋庸置疑,这是一类集函数、方程和不等式于一身的综合题,对学生的综合能力提出了很高的要求．从解法上看,根据绝对值的定义讨论去绝对值是解题的基本方向；而讨论,尤其是含参数的讨论,划分点在哪,为什么这样讨论,是教学的重点,也是难点．例如下面的问题.

问题2 已知f(x)=-x2+2x|x-a|.

(1)若a=-1,求f(x)在[0,2]上的值域;(2)若f(x)在区间[1,2]上是减函数,求实数a的取值范围;(3)是否存在实数a,使得f(x)≤x-a-a2在区间[1,2]上总成立,请求出所有这样的实数a;若不存在,请说明理由．

本题(2)(3)的参考解答如下:

综上，a∈[2,3]．

(3)令F(x)=f(x)-x+a+a2.

由题意,F(x)≤0在[1,2]上恒成立⟺F(x)在[1,2]上的最大值小于等于0．

综上a=1.

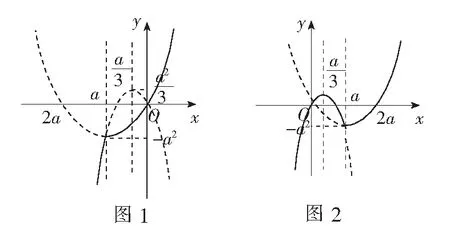
本题(3)的上述解答,笔者不尽赞同．F(x)=-x2+2x|x-a|-x+a2+a按x≥a和x0进行讨论．“这样讨论的依据是什么?”“我怎么想不到?”学生中经常会出现这样的疑问.

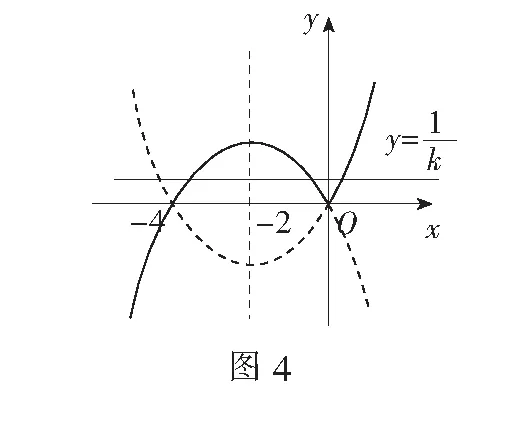
问题3 已知函数f(x)=x|x-a|,a∈R,g(x)=x2-1.

(1)当a=1时,解不等式f(x)≥g(x);

(2)记函数f(x)在[0,2]上的最大值为F(a),求F(a)的表达式．

本题(2)的参考解答如下:

当a≤0时,f(x)=x2-ax,则f(x)在区间[0,2]上是增函数,所以F(a)=f(2)=4-2a;

当0

综上，

以上解答中,讨论去绝对值的同时，考虑到了定义域区间,将划分点a分为在区间[0,2]的左侧、内部和右侧三种情形．但情形(2)与情形(3)中还将进行分类讨论,层次较多,学生很容易迷糊．

二、教学建议

毫无疑问,这类问题的解法多样,而且不同的切入点,解的难易程度不一样．为使学生能较快找准解题的切入点,在实际教学中,笔者提出以下教学建议,与同行探讨．

1.放低起点,让学生够得到

在教学中可从学生的实际出发,选择一些分类比较清晰的较为基础的问题,让学生尝试练习,加深体验,增强自信．例如:

评注 本题解法的切入点很多,可让学生进行多种尝试,增加体验．

2.理顺思路,让学生想得到

对一些较难的题,尤其是含参问题,分析时从学生熟悉的、合乎情理的角度切入,理顺思路,让学生想得到,这样才能收到较好的教学效果．

例3 问题2第(3)问.

解 依题意，f(x)≤x-a2-a即-x2+2x|x-a|-x+a2+a≤0,对x∈[1,2]恒成立,令F(x)=-x2+2x|x-a|-x+a2+a,当a≤1时,F(x)=x2-(2a+1)x+a2+a≤0对x∈[1,2]恒成立．由于F(x)在[1,2]上的图象是一段开口向上的抛物线弧,所以只要

当a>1时,因为F(1)=a2+3a-4>0,故不合题,综上可得a=1.

以上解法中,按a在定义域区间[1,2]的左中右侧三种情况去绝对值．但当a>1时,是否有必要再分11时,F(x)表达式中x-a的符号唯有x=1时是确定的．故先考虑F(1)在情理之中,起到了删繁就简的作用．

例4 问题3第(2)问

当a>0时,

综上，

F(a)

以上解法中,当a>0时,先不考虑x∈[0,2],然后视2为变量,a为定值,对2的位置进行讨论.这种变更变量的思想方法十分睿智,思路清晰．

3.拓展视界,让学生享受到

其实,根据定义分类讨论去绝对值,仅是解决这类问题的方法之一,利用绝对值的几何意义,绝对值的性质等方法处理也是常用方法．在教学中有机地渗透,有利于拓展学生的视界,培养思维能力,让学生更多地感受数学的灵活性和多样性，得到赏心悦目的享受．

例5 已知函数f(x)=x|x2-a|,若存在x∈[1,2],使得f(x)<2成立,求a的取值范围是______.

≥|(x-2)-(x-3)|=1.

所以S≤2且2

“局部含绝对值”的问题,是学生学习中的难点,也是教师教学中的难点．在教学中,我们对每一个问题的解决不可能是尽善尽美的,但我们可以考虑以下问题:(1)还有更好的解法吗?(2)学生最容易想到的切入点在哪儿呢?沿此思路做下去会遇到哪些障碍?(3)为排除这些障碍,我们教师可做些什么?毕竟教会学生思考是我们的目的．