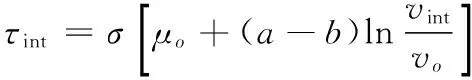断层演化过程中的周期和非周期地震滑移及非地震滑移----一维断层模型分析*

解孟雨 史保平

(中国北京100049中国科学院大学地球科学学院)



断层演化过程中的周期和非周期地震滑移及非地震滑移
----一维断层模型分析*

解孟雨*史保平

(中国北京100049中国科学院大学地球科学学院)

本文首先根据Dieterich和Ruina提出的含速率和状态的摩擦定律(Dieterich-Ruina定律)，基于一维弹簧-滑块模型推导了地震复发周期的解析表达式，然后将该近似解与数值模拟结果以及Barbot等的相关研究进行了对比分析．此外，本文还利用数值模拟与理论分析研究了断层周期和非周期演化的力学成因机制以及非地震滑移形成的另类力学机制，并讨论了一维弹簧-滑块模型的优点及其局限性．结果表明：① 震后滑移和自加速/成核阶段的持续时间在整个演化过程中不能被忽略；② 在修正后的复发周期模型中，复发周期的长短除了与断层特征尺度、作用于断层面上的有效正应力和远场加载速率相关外，还受Dieterich-Ruina定律中摩擦参数的取值以及临界滑移距离的影响；③ 当给定各个物理参数和几何参数时，目前所得到的解析近似解可以很好地估计地震的复发周期，其相对误差可小于5%；④ 在断层演化过程中，施加剪切应力加载会产生非周期的地震滑移，而在自加速/成核阶段后期或震后滑移阶段早期，施加较大的剪切应力加载，则会出现非地震滑移．

含速率和状态的摩擦定律 地震循环 地震复发周期 非地震滑移

引言

华北地区是中国大陆中强震多发地区之一，也是历史和现代仪器记录地震相对完整的区域．华北地震活动区主要包括4个地震带：郯城—营口地震带、华北平原地震带、汾渭地震带和银川—河套地震带．自公元1300年以来，M≥6的地震有49次，其中包括至少4次M≥8地震．京津唐地区位于自渤海湾至张家口NW--SE向的华北平原边缘，该地区曾发生过至少14次的M≥6破坏性地震，其中1679 年三河-平谷M8地震是该地区发生的最大破坏性地震．20世纪以来，发生在该地区的最强地震为1976年7月28日唐山MS7.8地震，该地震对唐山及其周边地区造成了约24万的人员伤亡以及巨大的财产损失．唐山MS7.8主震之后约15个小时，滦县又发生MS7.1地震．1976年11月15日，宁河又发生MS6.9地震，进一步加剧了对唐山及其周边地区的破坏程度．鉴于华北地区中强震位置分布的复杂性(Liuetal，2012)，40年来关于唐山大地震的成因机制以及学术界和社会公众所关注的地震预测方法一直是学术研究的难题．事实上，由于缺乏必要的观测手段和对发震断层物理/力学过程的深入了解，目前有关地震预测的研究仍然处于初步探索阶段．

从地质构造角度来讲，地壳内部构造地震的发生与断层内部的剪切形变相关．弹性回跳理论则给出了断层摩擦失稳的简单图像(Stein，Wysession，2003)：在长时间尺度的远场剪切应力加载下，断层两侧的剪切形变能不断累积，剪切应力也随之增加，当剪切应力超过断层本身的摩擦强度时，断层两侧突发相对滑动，部分形变能以地震波的形式传播至地表，从而造成相应的地表运动．当断层上的滑动停止后，剪切形变能再次逐步累积，形成了所谓的断层运动“黏滑机制”，该机制的提出建立在库仑(Coulomb)简单摩擦力学基础之上(Byerlee，1970，1978)．由此，Shimazaki和Nakata(1980)将地震重复发生(周期和非周期)的过程归结为3个理想化模型(图1)：周期模型、时间可预测模型和滑动可预测模型．图1中应力随时间的变化曲线给出了每个模型相对应的震前和震后的应力变化(静态应力降)．基于上述黏滑机制，对地震重复发生过程而言，现今广泛认可的控制因素可归结为：未来发震断层的构造剪切应力加载速率、断层本身的摩擦性质和周边地震对未来发震断层的影响(Stein，1999)．如果区域应力场出现了扰动(包含静态和动态应力变化及地壳内部流体压力变化等)，则断层上的应力加载或卸载会导致断层演化周期的改变或断层摩擦强度的变化，从而引起断层失稳时间的提前或推后．

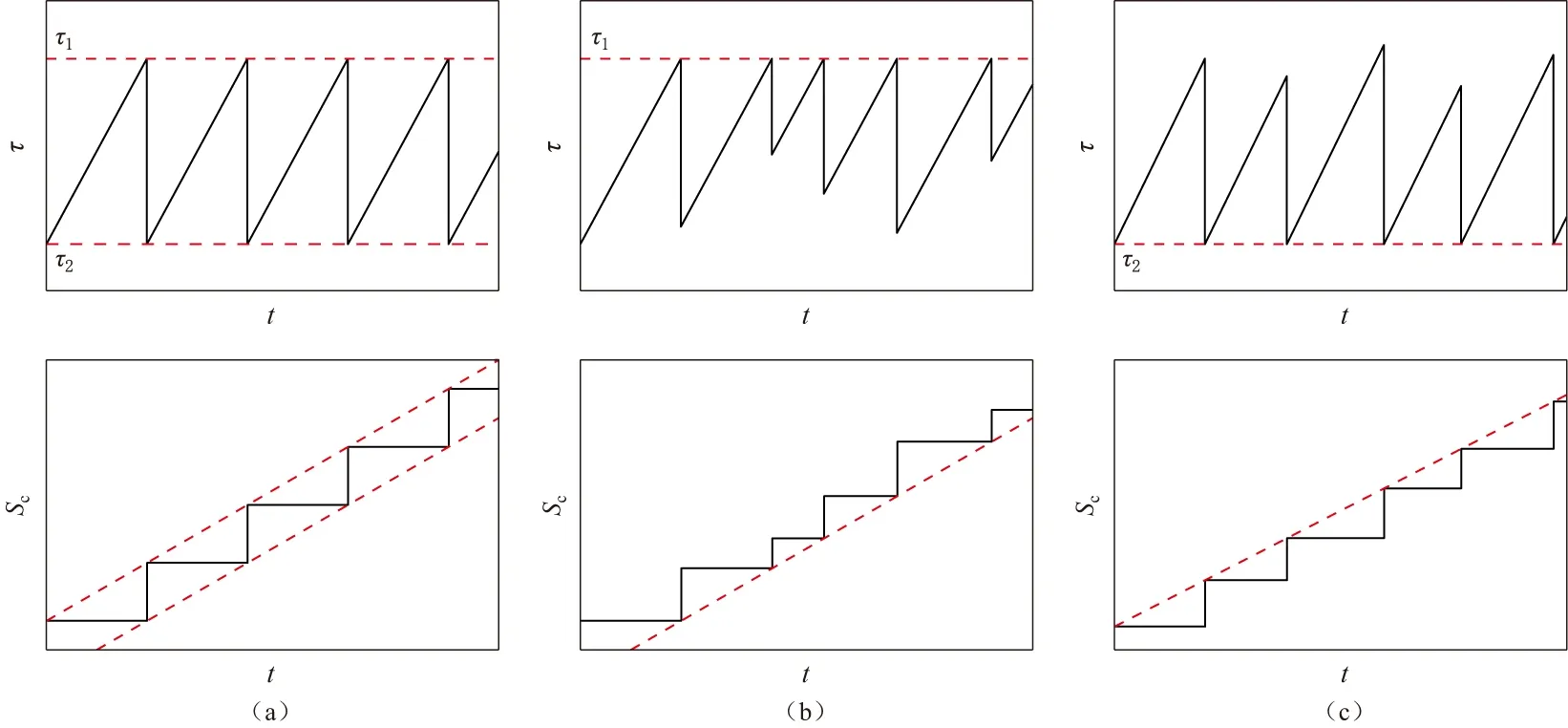
图1 地震复发模型示意图(引自Shimazaki，Nakata，1980)(a) 周期模型；(b) 时间可预测模型；(c) 滑动可预测模型τ1和τ2分别为地震发生后和地震发生前的应力，均为常数(虚线)，Sc为累积同震位移

图2a给出了受静态应力扰动后的库仑模型断层失稳示意图．可以看出，当断层上累积的剪切应力大于或等于断层摩擦强度时，断层会突发失稳．因此，当给定远场剪切应力加载速率时，应力扰动后断层失稳时间(虚线)的提前或延后量Δt仅与库仑应力变化的绝对大小有关，而与扰动的加载时刻无关(Gombergetal，1998; Harris，Simpson，1998; Perfettinietal，2003)．图2b指出了当断层摩擦强度下降时(虚线)，断层失稳也会出现时间上的提前．考虑到断层演化的复杂性，库仑模型对应力扰动下断层失稳时间的描述显得过于简单．例如，Harris和Simpson (1998)利用1857年加州M7.9地震和1906年旧金山M7.8地震的位错数据计算了库仑应力的大小，然后估计了应力影区的持续时间，通过对比两次地震之后地震发生的时间和空间信息，结果表明存在不符合库仑模型预测的地震，说明库仑模型并不能很好地确定地震的延后时间．

图2 库仑模型断层失稳示意图(a) 静态应力扰动引起的断层失稳(修改自仲秋，史保平，2012)；(b) 断层摩擦强度降低引起的断层失稳虚线为演化状态变化后的断层演化图，Δt为断层演化状态变化后第一次失稳发生时间的提前量

对发震断层的演化过程，目前地震学家比较一致的认识是断层滑动至少经历了4个明显不同的阶段(Stein，Wysession，2003)：① 闭锁阶段；② 自加速/成核阶段；③ 同震相；④震后松弛/滑移阶段．受地震观测数据的限制，我们对每个阶段的断层摩擦动力学过程及其复杂性知之甚少．岩石力学实验表明，断层摩擦过程与断层内部的滑移速率和状态直接相关(Marone，1998)．含速率和状态的摩擦定律(rate- and state-dependent friction law，简写为RSF定律)目前已普遍用于对发震断层孕育、成核及发震深度约束的研究中(Scholz，1998)．在此定律的框架下，有关断层演化、地震复发周期以及触发地震成因机制的数值分析与理论研究已在全球范围内得到了广泛关注(Perfettini，Avouac，2004a，b; Kanekoetal，2010; Barbotetal，2012; Kameetal，2013a)．而关于静态应力扰动后断层失稳时间的提前或推后的论述则最早来自Dieterich (1992，1994)余震触发机制的解析模型．在对帕克菲尔德地震断层的时空演化特征研究中，基于RSF定律中的Dieterich-Ruina定律(Dieterich，1992，1994；Segall, 2010; Bhattacharya, Rubin, 2014)，Barbot等(2012)给出了地震重复周期计算的解析表达式，即

(1)

式中：Δτs为应力降；η为描述断层面形状的几何参数，一般近似等于1(Dieterich，1992)；G为剪切模量；W为断层面的特征尺度，为断层长度的一半或断层面的半径(圆盘断层模型而言)；vpl为远场加载速率，通常取为常数；a和b分别为Dieterich-Ruina定律中的参数；σ为作用于断层面上的有效正应力；vco和vint分别为断层的同震滑移速率和震间滑移速率．显然，式(1)可以很好地估算地震重复周期，但从下文的理论分析与数值模拟中可以看出，式(1)对于估算断层的完整演化时间显然是不完全的，我们将在下文对式(1)进行修正．

本文首先利用Dieterich-Ruina定律，从一维弹簧-滑块模型出发，结合不同演化阶段所对应的近似描述公式，从理论上提出了计算地震复发时间的公式；然后利用四阶龙格库塔(4th-order Runga-Kutta)算法进行数值模拟计算，并对比验证该公式的可行性；另外，本文还将研究发震断层的周期和非周期演化的力学成因机制以及非地震滑移形成的另类力学机制．

1 基本原理

1.1 断层模型

假设断层满足平面应变条件，给定断层上任意滑动位移分布为δ(x)，那么由此滑动位移所产生的剪切应力沿断层面上的分布τs(x)可表示为(Beeler，2004; Rubin，Ampuero，2005; Bhattacharya，Rubin，2014)

(2)

式中，ν为泊松比．考虑到当给定远场剪切应力τ∞(x)时，作用于断层面上的剪切应力分布τ(x)可表示为

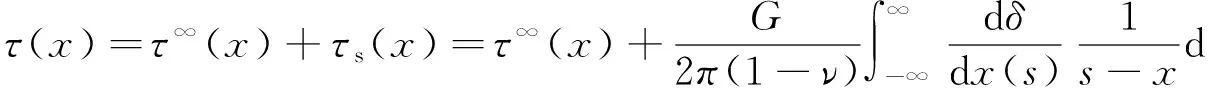
(3)

对式(3)在时间域求导可得

(4)

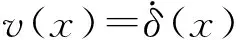
1.2 摩擦定律

RSF定律是由岩石力学实验结果所总结出的经验本构关系，该定律定量地刻画了断层内部的摩擦规律，也从物理上阐明了断层内部摩擦的复杂性，已成为研究断层演化、地震成核、动态破裂过程等震源物理现象的基础，并被广泛用于描述震源行为的系统性变化(Marone，1998)．RSF定律中描述摩擦系数的一般性方程为(Guetal，1984; Segall，2010)

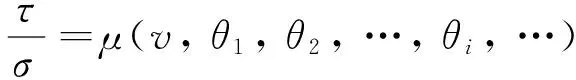
(5)

式中：τ为作用在断层面上的剪切应力；θi为状态变量(i=1，2，3，…，N)，是任何可以刻画接触面状态的变量，如颗粒大小、断层泥的孔隙度等(Segall，2010)；μ为断层面上的摩擦系数，与库仑摩擦过程不同的是，在RSF定律中，μ为断层滑移速率v和状态变量θi的函数．对于θi的演化，若保持正应力σ不变，则满足以下关系：

(6)

式中，i=1，2，3，…，N．式(5)和式(6)组成了完整的RSF定律(Guetal，1984; Segall，2010)．

1.3 Dieterich-Ruina定律

为使计算和分析更简单方便，通常采用单一状态变量θ的RSF定律．目前最常用的两个定律分别是Dieterich-Ruina定律和Ruina定律(Segall，2010; Bhattacharya，Rubin，2014)．在稳定状态或接近稳定状态时，两个定律的公式形式是一致的，但在其它状态下两者是不同的(Bhattacharya，Rubin，2014)．Dieterich-Ruina定律可以很好地解释滑动—约束—滑动测试中摩擦界面的愈合现象，但不能解释速度阶梯变化实验中应力演化到新的稳定状态时所需的位移与速率阶梯变化大小和正负符号无关；与之相反，Ruina定律则可以解释速度阶梯变化实验中的应力变化现象，但不能阐明上述愈合现象(Bhattacharya，Rubin，2014)．Nagata等(2012)针对Dieterich-Ruina定律提出了修正的摩擦定律，可以同时解释上述滑动—约束—滑动测试和速度阶梯变化实验中出现的现象．为便于讨论，考虑到摩擦定律的使用广泛程度，本文选用Dieterich-Ruina定律进行数值模拟与理论推导，其表达式为

(7)

(8)

式中：vo为参考速率；μo为稳定滑动且滑动速率为vo时的摩擦系数；θ为凹凸体的平均接触时间，即凹凸体之间接触的平均存在时间(Scholz，2002)；Dc为临界滑动距离，即彻底改变断层接触面摩擦状态所需的滑动距离(Marone，1998)；a和b分别为实验常数，a为“直接影响”系数，决定速率变化所引起的摩擦强度变化，b为“演化影响”系数，控制状态演化所引起的摩擦系数变化(Bhattacharya，Rubin，2014)，一般来讲，a和b均大于0，且具有相同的数量级，其取值范围为0.005—0.01(Dieterich，1994)．在剪切作用下，假定作用于断层面上的正应力始终保持不变，对式(7)在时间域求导，可得

(9)

(10)

显然，当a-b≥0时，断层的摩擦过程处于速度强化状态，此时断层的滑动是稳定的；而当a-b<0时，断层的摩擦过程处于速度弱化状态，断层的滑动可以是条件稳定，也可以是不稳定的(Scholz，1998)．

结合式(4)与式(9)，断层摩擦过程的数学描述可表示为

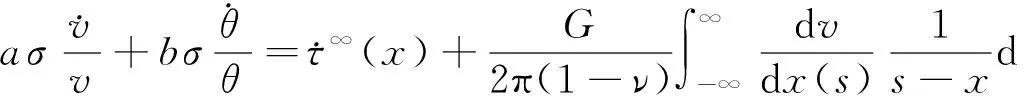
(11)

该式被广泛应用于断层成核和自发破裂过程的研究中．对于单一自由度的一维弹簧-滑块模型(图3)，滑块加载过程可由下式给出：

τ(t)=τ(0)+k(vplt-δ)，

(12)

式中：τ(0)为断层内部保留的初始应力；t为时间变量；k为弹簧的有效刚度系数，可表示为k=ηG/W．因此，对于一维弹簧-滑块模型，式(11)可简化为

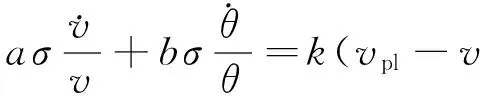
(13)

一维弹簧-滑块模型看似简单，但事实上包含了断层摩擦滑移破裂过程的3个基本要素：① 滑块的摩擦面，其代表了断层面；② 弹簧，k的取值代表了地壳的弹性性质和几何特征，弹簧用以积累弹性应变能，为断层自加速阶段提供必要的应变能；③ 稳定的远场加载速率，其模拟了稳定的板块运动，为断层应变能的积累提供动力来源(Segall，2010)．

图3 一维弹簧-滑块模型

当vpl恒定时，给定初始的速度v(0)和状态变量θ(0)，通过联立方程(8)与(13)，并采用数值计算方法求解方程组，即可模拟断层在时间域内的演化过程，其中当v→∞时，断层发生破裂失稳．为了避免v→∞这一非物理现象的发生，通常在数值求解过程中加入辐射衰减项 (Segall，2010)，如对式(12)在时间域内求导并加入衰减项后可得：

(14)

或

(15)

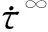
2 数值解

结合式(8)与式(15)，采用四阶龙格库塔算法可以求出在给定不同参数条件下一维断层的演化特征．表1给出了模拟计算中所使用的参数值．

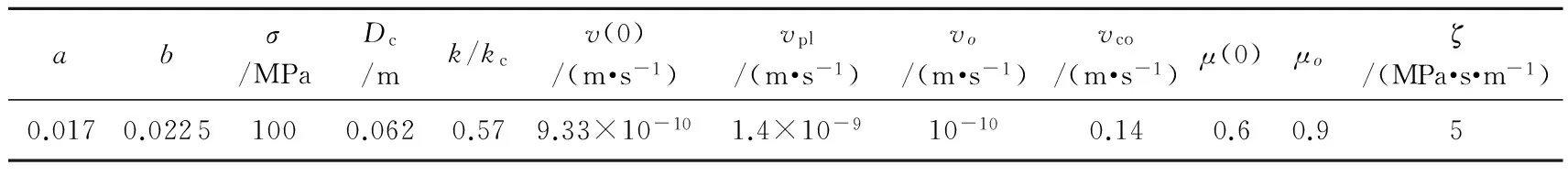
表1 模拟计算中使用的参数值(引自Kame et al, 2013b)

注：状态变量初始值θ(0)由v(0)和μ(0)求得.

图4给出了加入辐射衰减项后模拟得到的包括滑移速率和应力变化在内的断层演化过程．可以看出，在模拟计算开始的0—160年(从起始时刻至第一次失稳的时间段)内，计算结果与之后时间段的结果并不相同．在上述时间段内断层的演化受初始参量v(0)，θ(0)和介质参数的控制，所以改变v(0)和θ(0)会使得从起始时刻至第一次失稳时间段内的演化曲线发生明显变化，不过改变v(0)和θ(0)却不会影响之后时间段的演化情况．实际上第一次失稳后的演化仅受介质参数的影响，可以反映介质参数所控制的一维断层模型本身的演化特征，因此之后分析中不考虑0—160年内的演化情况．

图4 基于一维断层模型的滑移速率周期演化图(a)和相平面内的闭合轨迹图(b)Tr为断层模型的完整演化周期，黑色三角形为各个阶段的分界标志，下同

图4a给出了滑移速率的变化特征．可以看出，滑移速率随时间的变化呈现出明显的周期性特征，断层在失稳时刻的滑移速率可达0.14 m/s，图中曲线所呈现出的特征均与断层运动的黏滑机制一致．图4b给出了地震循环的4个主要阶段．模拟结果显示：断层闭锁阶段至少占总的演化周期Tr的70%，而自加速阶段、同震相和震后松弛/滑移阶段这3个阶段只占了30%Tr．

图5为一个地震循环周期内的一维断层演化图．由图4和图5可以看出，断层演化在时间上由4个主要阶段组成，每个阶段的持续时间是不同的. 如果以Tint，Tpre，Tco和Tpost分别代表断层演化过程中闭锁、自加速/成核、同震相和震后松弛/滑移阶段所经历的时间尺度，那么完整的断层演化周期Tr可表示为

Tr=Tint+Tpre+Tco+Tpost.

(16)

显然，断层所处的闭锁阶段的持续时间远远大于其它3个阶段持续时间的总和(图4和图5), 而成核阶段和震后滑移阶段的持续时间基本相当，即Tpre≈Tpost．与其它3个阶段相比，同震滑移的持续时间Tco一般为几秒至几分钟．另外，对应于每个阶段，Ω=vθ/Dc值的大小表现出明显差异：当断层处于震后滑移和闭锁阶段时，vθ/Dc<1；当断层处于自加

图5 一个地震循环周期内的一维断层演化图(a) 断层滑移速率演化图；(b) 断层模型中Ω=vθ/Dc随时间的变化

速/成核阶段时，vθ/Dc>1．如上所述，同震滑移在几秒到几分钟内完成，即Tco相对很小，因此在地震复发周期的计算中Tco可以忽略不计．由此，地震演化周期Tr可写为

Tr≈Tint+Tpre+Tpost.

(17)

3 断层演化周期的近似计算与相应数值解的对比

3．1 解析近似解

当断层演化处于自加速阶段并满足vθ/Dc≫1时，则Dieterich-Ruina定律中的状态方程，即式(8)可近似为

(18)

结合式(13)，则滑移速率的近似解为(Dieterich，1992，1994)

(19)

(20)

(21)

震后滑移开始于同震滑移的结束，因此在震后滑移起始时刻，滑移速率v近似等于vco，θ近似等于θco(Rubin，Ampuero，2005)．如果设定震后滑移阶段始于t=0，则震后滑移和闭锁阶段的滑移速率随时间变化的近似解为(Rubin，Ampuero，2005)

(22)

状态方程的解为

θ=θco+t.

(23)

(24)

式中，tp为震后滑移的持续时间尺度(震后滑移阶段始于t=0)，也是震后滑移的结束时刻和闭锁阶段的开始时刻．因此，我们称tp为断层演化过程中由震后滑移到闭锁阶段的转折

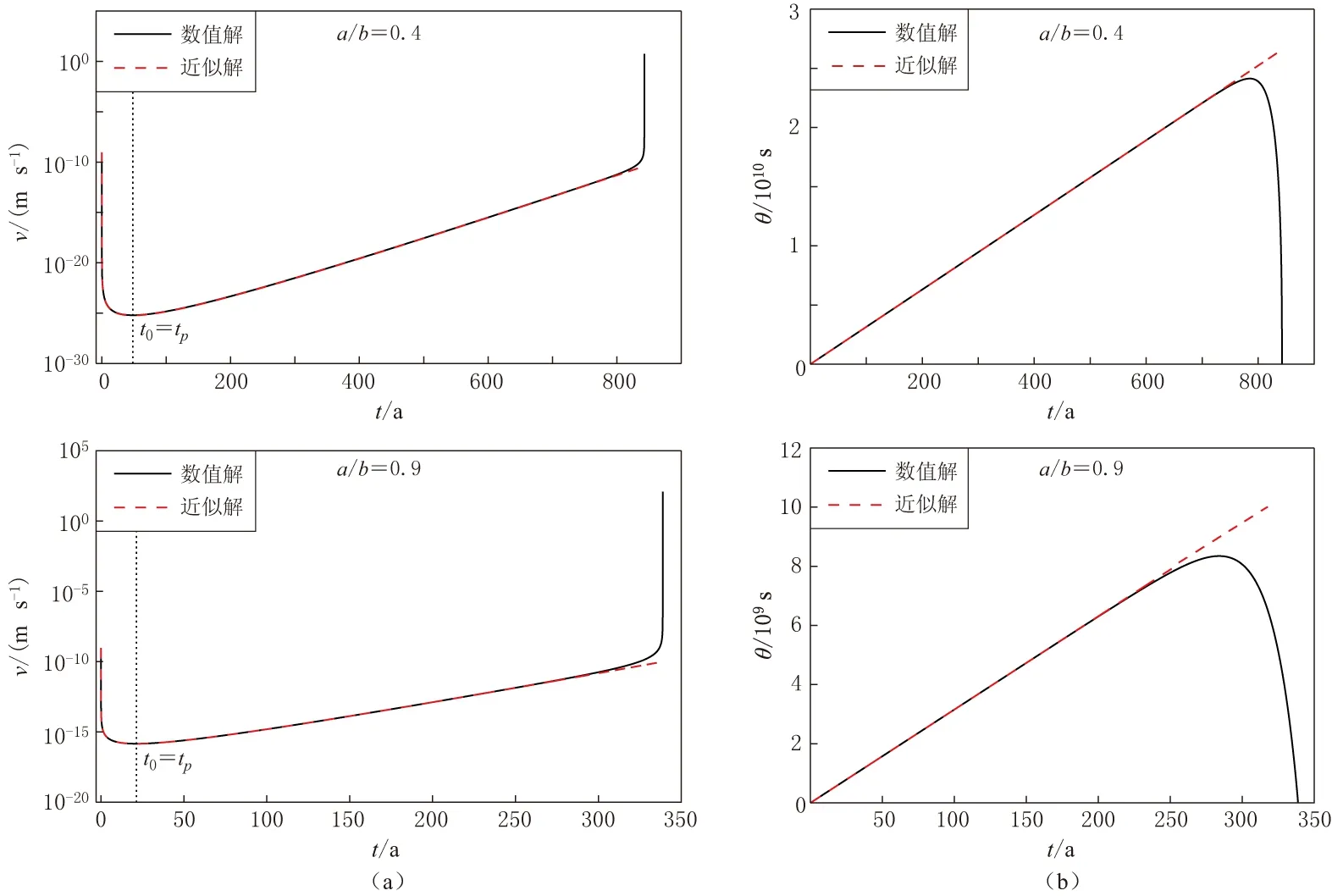
图6 滑移速率v(a)和状态变量θ(b)的近似解与数值解对比图

点．震后滑移所持续的时间尺度可近似为

(25)

(26)

(27)

对式(27)两边取对数后合并同类项，可得

(28)

那么则有

(29)

综合上述所得到的Tpre，Tpost和Tint，则断层演化周期的近似解可写为

(30)

(31)

其具体过程请参见附录.

比较式(30)与式(31)可以看出，Barbot等(2012)对地震循环周期的估计忽略了震后滑移和自加速/成核阶段所需的演化时间．在Dieterich(1994)的余震触发模型中，ta也为主震后余震的持续时间．Stein和Liu(2009)的研究也表明，在较小的加载速率下，例如大陆内部构造地震，余震的持续时间可能高达几百年．仲秋和史保平(2012)对1976年7月28日唐山MS7.8地震余震序列的分析表明，如果余震的触发机制可由Dieterich模型表示，那么该地震的余震持续时间ta大约为80—100年．在Dieterich-Ruina定律中，a和b的取值处于相同的数量级，如果断层能够完成自加速/成核过程，则必须有b>a，由此推断震后滑移阶段的持续时间Tpost可能会大于自加速/成核阶段的持续时间Tpre，且应处于相同的数量级．因此，式(31)等号右侧的第一、三项在断层演化周期的估算中是不能省略的．关于闭锁阶段滑移速率vint的估算，Rubin 和Ampuero(2005)给出了相应的近似解．对于一维断层模型，vint主要受k和kc的影响，一般来讲vint比远场加载速率vpl小2—3个数量级(Rubin，Ampuero，2005)．

3.2 近似解与数值模拟结果的对比

图7 不同a/b值情况下断层滑移速率和剪切应力的相图

表2 不同a/b值情况下近似解与数值解的对比

Table 2 Comparison of analytic approximate solutions with numerical solutions for differenta/bvalues

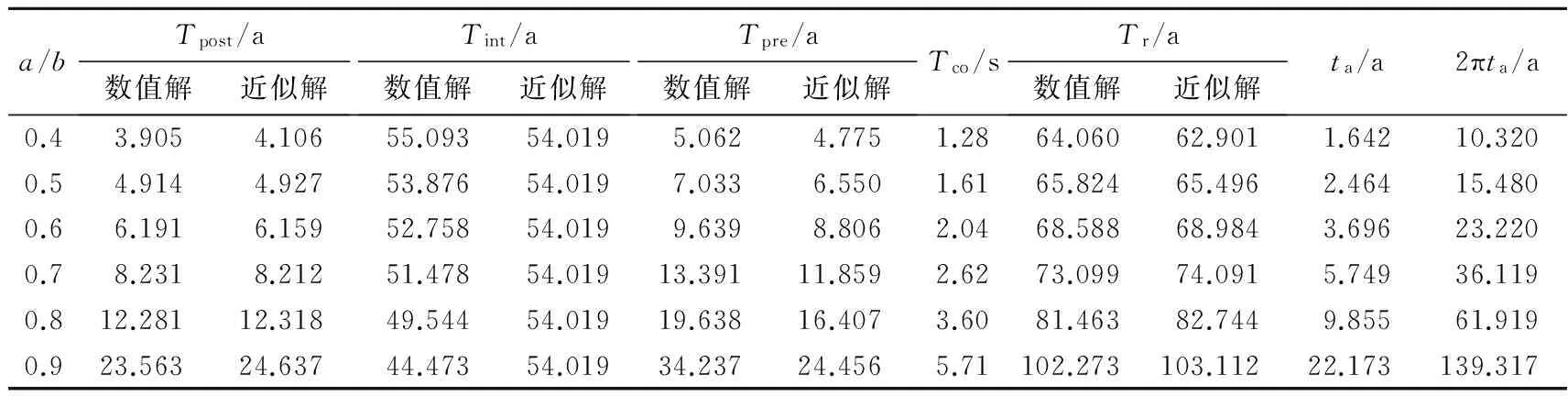
a/bTpost/a数值解近似解Tint/a数值解近似解Tpre/a数值解近似解Tco/sTr/a数值解近似解ta/a2πta/a0.43.9054.10655.09354.0195.0624.7751.2864.06062.9011.64210.3200.54.9144.92753.87654.0197.0336.5501.6165.82465.4962.46415.4800.66.1916.15952.75854.0199.6398.8062.0468.58868.9843.69623.2200.78.2318.21251.47854.01913.39111.8592.6273.09974.0915.74936.1190.812.28112.31849.54454.01919.63816.4073.6081.46382.7449.85561.9190.923.56324.63744.47354.01934.23724.4565.71102.273103.11222.173139.317

D'cDcTpost/a数值解近似解Tint/a数值解近似解Tpre/a数值解近似解Tco/sTr/a数值解近似解ta/a2πta/a10100.925100.786505.352540.192163.818141.25531.18770.094782.23376.150478.463550.26950.393252.878270.09681.90070.62715.49385.047391.11738.075239.232220.19420.157101.064108.03832.76128.2516.20154.019156.44715.23095.693110.05910.07950.57254.01916.37814.1263.1177.00978.2237.61547.8460.55.0335.03925.27627.0108.1957.0631.5538.50539.1123.80823.9230.22.0122.01610.11410.8043.2762.8250.6215.40215.6451.5239.5690.11.0051.0085.0575.4021.6381.4130.317.7017.8220.7624.785

(32)

(33)

4 剪切应力加载作用下的断层非周期地震滑移

当断层在演化过程中受到应力扰动后，会使得断层运动加速或减速，进而产生非周期的地震滑移．以成核阶段为例(图8)，由于断层在该阶段满足vθ/Dc≫1，所以可利用式(8)和式(13)推导出当t0时刻滑移速率为v0时，断层的失稳时间(未经应力扰动)为(Dieterich，1992，1994)

图8 施加和未施加正向静态剪切应力扰动时的滑移速率演化示意图实线为未扰动时的演化，虚线为存在扰动时的演化，t0为施加静态剪切应力扰动的时刻，T和Tv分别为未扰动时和扰动后从t0时刻至断层模型失稳所需的时间

(34)

而在t0时刻受静态剪切应力扰动后，断层的失稳时间为

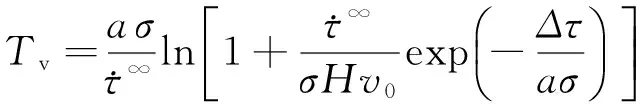
(35)

式中，Δτ为断层受到的静态剪切应力扰动. 失稳时间的提前或推后量为Δt=|T-Tv|．不难看出，只要施加在成核阶段的静态剪切应力扰动非零，那么一定会导致失稳时间的提前或推后，即成核阶段的持续时间会发生变化，进而产生非周期的地震滑移．而对于地震循环的其它阶段，若施加静态剪切应力扰动也会产生同样的现象，更为详细的讨论请参阅解孟雨和史保平(2016)文章．

5 非地震滑移

从静态剪切应力加载产生的非地震滑移图(图9)中可以看出，当断层随时间的演化过程接近于自加速/成核阶段的后期或震后滑移阶段的早期，且断层出现绝对值较大的剪切应力加载时，断层可以发生非地震滑移，从而也能打破断层演化的周期性．图9a给出了类似于脉冲的滑移速率扰动，其脉冲幅值远远小于同震滑移的速度值(0.14 m/s)，基本与远场加载速率vpl相当．图9b则分别给出了相应的状态变量随时间的变化．在非地震滑移发生之后，可以再次出现新的同震滑移现象，但所需的时间间隔远小于未经应力扰动时的演化周期(图9a)．

图9c则以相图的形式给出了断层上剪切应力与滑移速率之间的演化关系. 图9c中出现的现象与Kame等(2013a)采用修正的RSF定律(Nagataetal, 2012)和一维弹簧-滑块模型得到的数值模拟结果一致．Kaneko和Lapusta(2008)利用随深度变化的摩擦本构关系，也得到了非地震滑移现象．Barbot等(2012)在对帕克菲尔德地震重复发生过程的数值模拟中也出现了重复的非地震滑移．不过这些非地震滑移现象的出现有违于Dieterich(1992，1994)近似解的预测．

图9 正向(左)和负向(右)静态剪切应力加载产生的非地震滑移(a) 滑移速率v演化图；(b) 状态变量θ演化图；(c) 断层面上剪切应力τ和滑移速率v的相图黑线和红线分别为未受应力扰动和受应力扰动时一维弹簧-滑块模型的演化情况，τss和vss分别为稳定状态下断层面上的剪切应力和滑移速率

6 讨论与结论

本文在模拟计算中使用的是一维弹簧-滑块模型，该模型相对简单，虽然未考虑断层面的形态、非均匀性和非弹性的影响，但却能突出断层的基本物理特征，而且计算简单，有助于我们定性理解地震过程，进而为更深入的研究提供方向．一维弹簧-滑块模型等价于空间上滑移和应力均匀分布的断层模型(Rice，1983)，可以用来研究不同情况下断层模型的一阶近似情况 (Dieterich，1981)，能够突出其基本物理特征，进而为研究震源机制提供线索．例如，通过对一维弹簧-滑块模型的分析认识到，在描述该模型稳定性时需引进临界弹簧刚度系数kc，并且只有当弹簧的刚度系数满足k

基于Dieterich-Ruina定律和一维弹簧-滑块模型，本文利用解析模型与数值模拟相结合的原则探讨了断层演化过程中地震重复发生周期以及非地震滑移形成的可能力学机制．初步结论如下：

1) 数值模拟结果显示断层的整体演化至少包含4个主要阶段，即闭锁阶段、自加速/成核阶段、同震相和震后滑移阶段，其间如果断层受到外来应力加载的扰动，断层演化周期会被打断，从而造成断层失稳时间的提前或推后．

2) 与库仑模型所给出的时间提前量或推后量不同的是，当断层演化处于自加速/成核阶段时，失稳时间的提前量或推后量Δt的大小取决于应力加载的时刻．当正向应力加载作用于震后滑移阶段的早期或负向应力加载作用于自加速阶段的晚期(或同震滑移发生前)时，断层演化过程中会出现非地震滑移现象，具体表现为脉冲形的滑移速率，其幅值与远场加载速率相当．如今有关非地震滑移现象的讨论已成为全球关于地震成因和地震预测研究的热点(Perfettiniet al，2010;Noda，Lapusta，2013;Shirzaeiet al，2014;Avouac，2015;Uchidaet al，2016)，因此，目前的模拟计算结果可以为非地震滑移的成因提供新的认识．

3) 基于对数值模拟结果的认识，本文给出了估算地震重复发生周期(断层演化循环)的解析近似解，其中，断层演化周期除了与断层的特征尺度、远场加载速率和作用于断层面上的正应力相关外，同时也是Dieterich-Ruina定律中摩擦系数a，b以及临界滑移距离Dc的函数．同前人工作的最主要区别在于，本文工作进一步考虑了震后滑移阶段和自加速/成核阶段对断层整体演化的贡献．与数值模拟结果的比较也进一步表明，目前的近似解对演化各个阶段以及整个地震演化持续时间均给出了很好的近似．

需要强调的是，目前的工作对于断层演化过程的认识仍然是初步和粗浅的，真实断层几何状态和断层内部物理/力学结构的复杂性尚未考虑，因此，探索地震成因背后的摩擦力学机制仍需更为深入细致的研究工作，包括对理论、实验、观测以及方法等的进一步认识．

附录 地震演化周期Tr的推导过程

应力降Δτ满足(Barbotetal，2012)

(A1)

另外，Barbot等(2012)还假定在应力降发生前后断层均为稳定状态且两个稳定状态分别处于同震相和闭锁阶段，则有

(A2)

(A3)

式中，τco和τint分别为同震相和闭锁阶段的应力值. 式(A3)减去式(A2)可得

(A4)

进而有

(A5)

或

(A6)

解孟雨，史保平. 2016. 数值模拟静态应力扰动下的断层失稳: 结果分析兼与Dieterich模型和Coulomb模型的对比[J]. 地球物理学报，59(2): 593--605.

Xie M Y，Shi B P. 2016. Numerical simulation of fault instability due to an arbitrary static stress perturbation: A comparison with the Dieterich model and Coulomb failure model[J].ChineseJournalofGeophysics，59(2): 593--605 (in Chinese).

仲秋，史保平. 2012. 1976年MS7.8唐山地震余震序列持续时间及对地震危险性分析的意义[J]. 地震学报，34(4)：494--508．

Zhong Q, Shi B P. 2012. Aftershock time duration of the 1976MS7.8 Tangshan earthquake and implication for seismic hazard[J].ActaSeismologicaSinica, 34(4): 494--508 (in Chinese).

Avouac J-P. 2015. From geodetic imaging of seismic and aseismic fault slip to dynamic modeling of the seismic cycle[J].AnnuRevEarthPlanetSci，43(1): 233--271.

Barbot S，Lapusta N，Avouac J-P. 2012. Under the hood of the earthquake machine: Toward predictive modeling of the seismic cycle[J].Science，336(6082): 707--710.

Beeler N M，Lockner D A. 2003. Why earthquakes correlate weakly with the solid earth tides: Effects of periodic stress on the rate and probability of earthquake occurrence[J].JGeophysRes，108(B8): 2391.

Beeler N M. 2004. Review of the physical basis of laboratory-derived relations for brittle failure and their implications for earthquake occurrence and earthquake nucleation[J].PureApplGeophys，161(9/10): 1853--1876.

Belardinelli M E，Bizzarri A，Cocco M. 2003. Earthquake triggering by static and dynamic stress changes[J].JGeophysRes，108(B3): 2135.

Bhattacharya P，Rubin A M. 2014. Frictional response to velocity steps and 1-D fault nucleation under a state evolution law with stressing-rate dependence[J].JGeophysRes，119(3): 2272--2304.

Byerlee J. 1970. The mechanics of stick-slip[J].Tectonophysics，9(5): 475--486.

Byerlee J. 1978. Friction of rocks[J].PureApplGeophys，116(4/5): 615--626.

Dieterich J H. 1978. Time-dependent friction and the mechanics of stick-slip[J].PureApplGeophys，116(4/5): 790--806.

Dieterich J H. 1979. Modelling of rock friction: 1. Experimental results and constitutive equations[J].JGeophysRes，84(B5): 2161--2168.

Dieterich J H. 1981. Constitutive properties of faults with simulated gouge[C]∥MechanicalBehaviorofCrustalRocks:TheHandinVolume. Washington DC: American Geophysical Union：103--120.

Dieterich J H. 1992. Earthquake nucleation on faults with rate- and state-dependent strength[J].Tectonophysics，211(1/2/3/4): 115--134.

Dieterich J H. 1994. A constitutive law for rate of earthquake production and its application to earthquake clustering[J].JGeophysRes，99(B2): 2601--2618.

Gomberg J，Blanpied M L，Beeler N M. 1997. Transient triggering of near and distant earthquakes[J].BullSeismolSocAm，87(2): 294--309.

Gomberg J，Beeler N M，Blanpied M L，Bodin P. 1998. Earthquake triggering by transient and static deformation[J].JGeophysRes，103(B10): 24411--24426.

Gu J C，Rice J R，Ruina A L，Tse S T. 1984. Slip motion and stability of a single degree of freedom elastic system with rate and state dependent friction[J].JMechPhysSolids，32(3): 167--196.

Harris R A，Simpson R W. 1998. Suppression of large earthquakes by stress shadows: A comparison of Coulomb and rate-and-state failure[J].JGeophysRes，1032(B10): 24439--24451.

Kame N，Fujita S，Nakatani M，Kusakabe T. 2013a. Effects of a revised rate- and state-dependent friction law on aftershock triggering model[J].Tectonophysics，600: 187--195.

Kame N，Fujita S，Nakatani M，Kusakabe T. 2013b. Earthquake cycle simulation with a revised rate- and state-dependent friction law[J].Tectonophysics，600 : 196--204.

Kaneko Y，Lapusta N. 2008. Variability of earthquake nucleation in continuum models of rate-and-state faults and implications for aftershock rates[J].JGeophysRes，113(B12): B12312.

Kaneko Y，Avouac J-P，Lapusta N. 2010. Towards inferring earthquake patterns from geodetic observations of interseismic coupling[J].NatGeosci，3(5): 363--369.

Liu M，Stein S，Wang H. 2012. 2000 years of migrating earthquakes in North China: How earthquakes in midcontinents differ from those at plate boundaries[J].Lithosphere，22(2): 33--44.

Marone C. 1998. Laboratory-derived friction laws and their application to seismic faulting[J].AnnuRevEarthPlanetSci，26(1): 643--696.

Nagata K，Nakatani M，Yoshida S. 2012. A revised rate- and state-dependent friction law obtained by constraining constitutive and evolution laws separately with laboratory data[J].JGeophysRes，117(B2): B02314.

Noda H，Lapusta N. 2013. Stable creeping fault segments can become destructive as a result of dynamic weakening[J].Nature，493(7433): 518--521.

Parsons T. 2005. A hypothesis for delayed dynamic earthquake triggering[J].GeophysResLett，32(4): L04302.

Perfettini H，Schmittbuhl J，Cochard A. 2003. Shear and normal load perturbations on a two-dimensional continuous fault: 1. Static triggering[J].JGeophysRes，108(B9): 2408.

Perfettini H，Avouac J-P. 2004a. Postseismic relaxation driven by brittle creep: A possible mechanism to reconcile geodetic measurements and the decay rate of aftershocks，application to the Chi-Chi earthquake，Taiwan[J].JGeophysRes，109(B2): B02304.

Perfettini H，Avouac J-P. 2004b. Stress transfer and strain rate variations during the seismic cycle[J].JGeophysRes，109(6): 117--132.

Perfettini H，Avouac J-P，Tavera H，Kositsky A，Nocquet J-M，Bondoux F，Chlieh M，Sladen A，Audin L，Farber D L，Soler P. 2010. Seismic and aseismic slip on the Central Peru megathrust[J].Nature，465(7294): 78--81.

Ranjith K，Rice J R. 1999. Stability of quasi-static slip in a single degree of freedom elastic system with rate and state dependent friction[J].JMechPhysSol，47(6): 1207--1218.

Rice J R. 1983. Constitutive relations for fault slip and earthquake instabilities[J].PureApplGeophys，121(3): 443--475.

Rubin A M，Ampuero J-P. 2005. Earthquake nucleation on (aging) rate and state faults[J].JGeophysRes，110(B11): B11312.

Ruina A. 1983. Slip instability and state variable friction laws[J].JGeophysRes，88(B12): 10359--10370.

Ryder I. 2006.ElasticandViscoelasticModellingofPostseismicMotionandFaultStructures[D]. Oxford: Oxford University: 12.

Scholz C H. 1998. Earthquakes and friction laws[J].Nature，391(6662): 37--42.

Scholz C H. 2002.TheMechanicsofEarthquakesandFaulting[M]. New York: Cambridge University Press: 85，266--267.

Segall P. 2010.EarthquakeandVolcanoDeformation[M]. Princeton: Princeton University Press: 332，338--339，349--350.

Shimazaki K，Nakata T. 1980. Time-predictable recurrence model for large earthquake[J].GeophysResLett，7(4): 279--282.

Shirzaei M，Burgmann R，Uchida N，Pollitz F，Matsuzawa T. 2014. Seismicversusaseismic slip: Probing mechanical properties of the northeast Japan subduction zone[J].EarthPlanetSciLett，406: 7--13.

Stein R S. 1999. The role of stress transfer in earthquake occurrence[J].Nature，402(6762): 605--609.

Stein S，Wysession M. 2003.AnIntroductiontoSeismology，Earthquakes，andEarthStructure[M]. Malden: Blackwell Publishing: 215--217.

Stein S，Liu M. 2009. Long aftershock sequences within continents and implications for earthquake hazard assessment[J].Nature，462(7269): 87--89.

Uchida N，Iinuma T，Nadeau R M，Burgmann R，Hino R. 2016. Periodic slow slip triggers megathrust zone earthquakes in northeastern Japan[J].Science，351(6272): 488--492.

The periodic and aperiodic slip during earthquake faulting and aseismic faulting slip: 1D fault model analysis

Xie Mengyu*Shi Baoping

(CollegeofEarthScience，UniversityofChineseAcademyofSciences，Beijing100049，China)

With a simple 1D spring-slide block model governed by Dieterich-Ruina law，this study derived an approximate analytical solution used to calculate the earthquake recurrence time and compared its approximate solution with previous results given by Barbotetal. The comparison between approximate solutions and the results by numerical simulation also demonstrated that current solution gives us a better approximation compared with previous result. Furthermore，it should be emphasized that，because only 40% to 80% of earthquake recurrence time belongs to interseismic stage，therefore，the duration of postseismic and nucleation/preseismic stage could not be ignored in the whole faulting process. Specifically，the time scale of earthquake recurrence in current earthquake recurrence model is not only related to the characteristic dimension of fault，the effective normal stress and remote loading rate，but also strongly depends on the values of the frictional parameters in the Dieterich-Ruina law and the critical distance obtained from laboratory. It is necessary to point out that，if all parameters we used represent a real situation in the earth，the approximate solution proposed in the present paper can give us an excellent estimation of earthquake recurrence time for a given tectonic region，of which relative error is less than 5%. Moreover，numerical simulation and theory are also used to study the mechanical mechanisms which cause the periodic and aperiodic evolution of the earthquake faulting and aseismic faulting slip. In addition，this paper also discussed the limitations and advantages of using 1D spring-slide block model to describe the elasticity in modeling evolution of fault. And it is found that applying shear stress loading during evolution of earthquake faulting can cause aperiodic evolution. Specially，applying shear stress loading at late nucleation/preseismic stage or early postseismic stage will lead to aseismic faulting slip.

rate- and state-dependent friction law; earthquake cycle; earthquake recurrence time; aseismic slip

10.11939/jass.2016.04.006.

国家国际科技合作专项(2015DFA21260)、北京市高校共建项目、国家基金委(41574040)和中国科学院创新团队项目(KZZD-EW-TZ-19)共同资助.

2016-03-15收到初稿，2016-05-27决定采用修改稿.

10.11939/jass.2016.04.006

P315.3

A

解孟雨, 史保平. 2016. 断层演化过程中的周期和非周期地震滑移及非地震滑移----一维断层模型分析. 地震学报, 38(4): 590--608.

Xie M Y, Shi B P. 2016. The periodic and aperiodic slip during earthquake faulting and aseismic faulting slip: 1D fault model analysis.ActaSeismologicaSinica, 38(4): 590--608.doi:10.11939/jass.2016.04.006.

*通讯作者 e-mail: jiemengyu13@mails.ucas.ac.cn