贵州雷电流幅值累积概率分布公式探讨

吴安坤, 邵莉丽, 吴仕军, 张淑霞

(1.贵州省气象灾害防御技术中心, 贵州 贵阳 550081;2.成都信息工程大学 大气科学学院, 四川 成都 610225)



贵州雷电流幅值累积概率分布公式探讨

吴安坤1,2, 邵莉丽1, 吴仕军1, 张淑霞1

(1.贵州省气象灾害防御技术中心, 贵州 贵阳 550081;2.成都信息工程大学 大气科学学院, 四川 成都 610225)

在IEEE 工作组和国内电力行业规程中采用的雷电流幅值概率分布特性的基础上,提出IEEE、规程两种幅值分布公式。采用贵州省近9年闪电实时监测数据拟合两种分布公式形式,并从累积概率、概率密度方面进行了分析。结果表明,采用IEEE 分布表达形式的雷电流幅值累积概率曲线更接近真实情况,规程形式拟合的概率密度曲线与真实情况差异性较大,若直接进行相关工程计算,产生的误差会更大。通过对拟合的IEEE分布公式进一步修正,提出更适宜于本地的雷电流幅值累积概率分布公式。

雷电流幅值; 累积概率; 概率密度; 相关误差

0 引 言

雷电流幅值概率是表征雷电活动频度,计算雷击闪络率的必要参数,其取值精确性直接关系到雷击闪络率的计算精确性。国内外使用的雷电流幅值概率分布表达式不同。国内先后经过3次修订[1],目前使用的是依据1962～1987年的磁钢棒检测结果[2],基于97个雷击塔顶负极性雷电流幅值数据进行回归,其表达式被电力行业规程DL/ T620—1997《交流电气装置的过电压保护和绝缘配合》推荐[3]。国际上,文献[4-5]对不同区域雷电流幅值分布进行了研究,归纳了相应的雷电流幅值累积公式。电气和电子工程师协会(IEEE)推荐的雷电流累积频率采用近似对数正态分布式,提出雷电流为2～200 kA时,推荐使用Anderson-Erikson实测数据提出的雷电流幅值的概率分布[6]。

雷电活动很大程度上与区域性的地理条件、地质土壤、气象环境等因素密切相关,幅值概率分布存在区域差异性,仅采用推荐的公式,并不能精确地反映某区域的雷电流幅值概率分布情况。因此,2007年王巨丰[7]等对采用磁带法进行输电线路雷电参数实测数据进行分析,提出桂林地区雷电流幅值频率分布曲线。2011年李家启[8]等采用对数正态分布函数拟合雷电流幅值频率分布曲线,更准确地为重庆地区(典型库区地貌区域)的城市规划和防雷减灾活动提供了理论依据。

近年来,随着全国闪电监测网的建立和监测资料随时间的逐步积累,为进一步研究雷电流幅值概率分布、掌握雷电活动规律、制定防雷减灾规划提供科学依据。本文采用贵州省近9年(2006～2014年)累积的雷电监测数据,通过分析比较现有的拟合雷电流幅值概率分布形式,提出雷电流幅值概率计算公式,并对其进行修正。

1 资料来源

资料来源于贵州省闪电监测定位系统的监测数据,该系统由12个ADTD闪电定位探测子站和1个数据处理中心站组成,每个ADTD闪电定位探测子站的探测范围约为200 km,实现对全省范围内的雷电实时监测。当闪电发生时,相邻接收到电磁信号的单站将测到的闪电发生时间、方位、强度和电磁辐射信号实时传输给中心站进行实时定位处理,由中心站通过计算后提供每次闪电的信息,包括闪击发生的时间、经纬度位置、强度、极性、陡度等。

2 拟合形式比较

目前,雷电流累积频率分布主要包括规程推荐和IEEE推荐两种。国外许多国家的雷电流累积频率分布公式采用IEEE推荐公式,而我国则采用相关行业规程中的公式。

IEEE推荐的雷电流累计频率为[4-5]

(1)

式中:I——雷电流;a——样本中值电流;b——曲线的指数变化程度。

规程推荐的雷电流累计频率为[2-3,7]。

lgPI=-I/a

(2)

本文提取2006～2014年闪电定位系统监测到的4 599 715次闪电数据样本,其中正闪电为172 259次,不到总闪(正闪+负闪)的4%。正闪、负闪及总闪的平均雷电流幅值分别为53.50 kA、34.53 kA、35.24 kA,其幅值累积概率达到80%的分别为73.1 kA、45.3 kA、46.2 kA,幅值高密区分别集中在22.6 kA、25.4 kA、25.5 kA附近。

采用规程推荐、IEEE推荐两种形式,分别从累积概率分布、概率密度分布方面与实际监测的统计值进行比较。

2.1 累积概率分布

对监测样本按照两种形式进行最优化拟合,拟合结果比较如表1所示。拟合优度R2均达到0.9以上,可以认为各参数的取值对于监测数据的实际分布反演都很理想,但IEEE推荐公式的R2更理想。此外,两种分布式总闪与负闪的参数取值相近,与正闪对应的参数值相差较大,这是由于闪电中绝大部分为负闪,占总闪数的96.3%。

表1 拟合结果比较

拟合形式正闪+负闪abR2负闪abR2正闪abR2式(2)81．10—0．949579．71—0．9480119．9—0．9661式(1)28．942．8750．999228．602．9200．999140．502．4150．9992

累计概率分布如图1所示。进一步分析表明,采用IEEE推荐形式的回归拟合效果比用规程推荐形式的拟合效果好,尤其是正闪与统计累积概率曲线几乎一致,拟合效果比负闪效果略强,这与文献[9]提出的正闪雷电流幅值的拟合效果比负闪效果相对略弱存在差异。

正闪、负闪及总闪对应的三条曲线(统计累积概率、IEEE推荐形式及规程推荐曲线)分别在约45 kA、35 kA、35 kA处相交。在交叉点左侧,同一电流值所对应的累积概率要大于规程推荐值,最大差值达到0.2;累积值略小于规程推荐值,最大差值小于0.05。在交叉点右侧,同一电流值所对应的累积概率要小于规程推荐值,最大差值达到0.1;与IEEE推荐值相差不大。

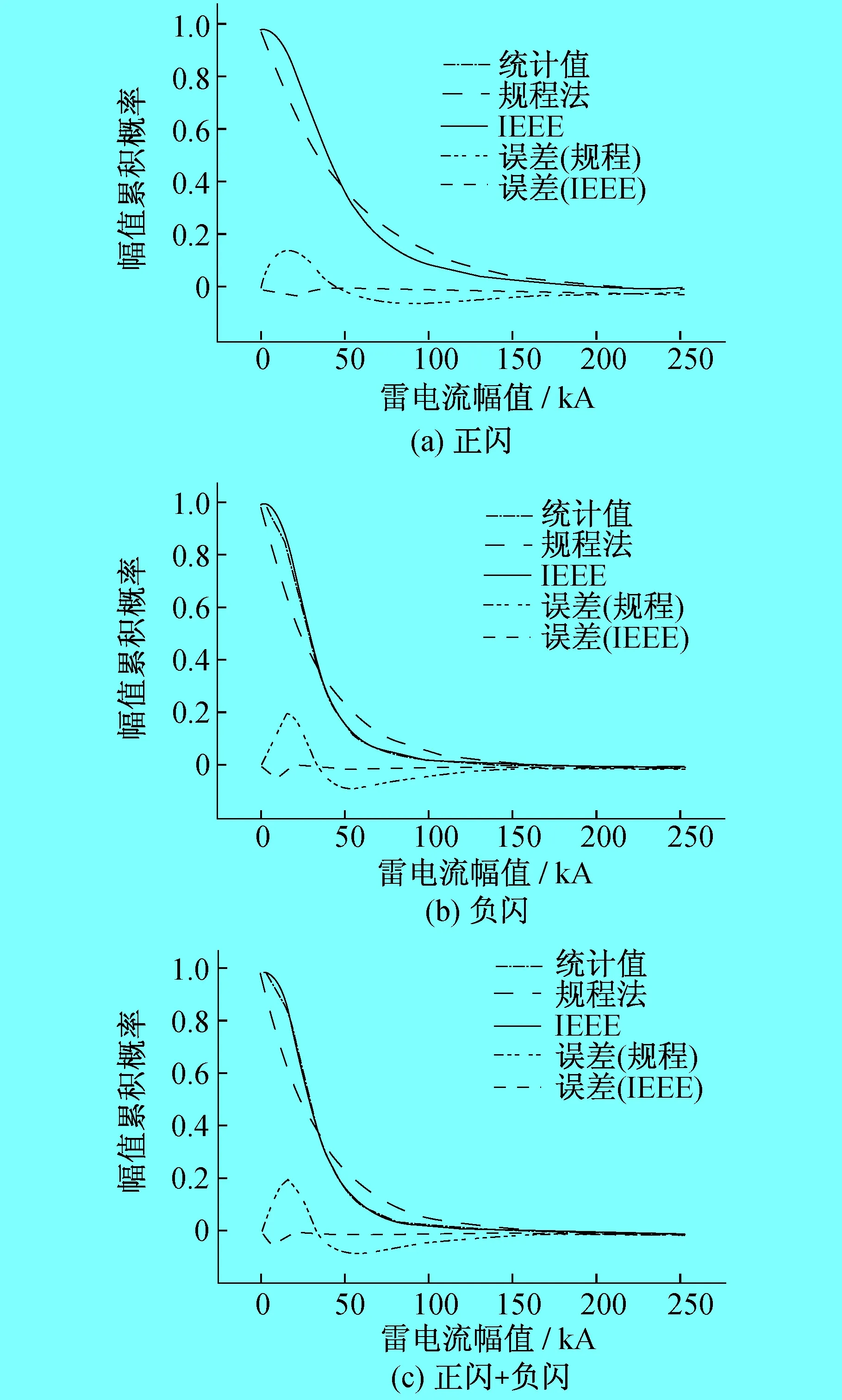
图1 累积概率分布

此外,规程推荐形式为单纯的对数式,拟合曲线偏向平缓,三种情况下的拟合曲线与监测数据的统计值存在明显的差异。

2.2 概率密度分布

雷电流幅值概率密度是描述各连续雷电流幅值发生频次所占的比率。本文选取的分布曲线分辨率为0.1 kA,即概率密度值对应的最小刻度为0.1 kA。针对两种不同的拟合形式,分别比较正闪、负闪及总闪的概率密度与监测数据统计分布曲线对比,如图2所示。

统计值曲线中,正闪、负闪及总闪均呈先上升后下降的分布规律。经正闪、负闪合并后的总闪概率密度分布特点与负闪极其相似,存在两个峰值点(约在22.6 kA、9.3 kA),即在密度高值区之前存在一个次高值区;正闪幅值密度分布在各个区间均有较大波动,即在大的分布特征下呈现小的“波浪”形变化。

IEEE推荐的概率密度曲线与统计概率密度曲线特征呈大致相似的分布变化,能够较合理地反映正闪的“毛刺”分布,跨过极高峰值点后与负闪、总闪曲线基本重合,但对于次峰值区域概率密度的变化情况存在差异。相比规程推荐的概率密度曲线,幅值分布高密区均集中在0 kA附近,与实际情况严重不符。

通过计算输变电线路绕击闪络率,进一步对比两种分布形式的差异。绕击闪络率采用的一般公式[6]为

(3)

Dc(I)=Imax-Ic

式中:Ng——雷击大地密度;L——线路长度;Ic——临界雷电流;Imax——最大雷电流;f(I)——雷电流幅值概率密度。 式(3)中,绕击闪络率与雷电流概率密度在Ic与Imax之间的积分有对应函数关系,即绕击闪络率、雷电流幅值概率密度曲线与Ic与Imax之间的面积分布大小有关。例如220 kV输变电线路,分析两种分布式得到的概率密度曲线围成的面积范围:若用规程推荐计算线路绕击闪络率,则少计算了区域A部分的面积,误差达到40%以上,在一定程度上解释了当前超高压线路中实际绕击闪络率普遍高于计算值的原因[8];若用IEEE推荐的计算,则多计算了少部分的区域B,误差不到5%。两种方法对比,工程上计算雷电绕击闪络率时用规程法推荐的公式误差太大。

因此,规程法所对应公式的表达形式不适于描述雷电流概率分布[10-11]。此外,IEEE推荐形式的拟合效果虽优于规程推荐形式,若直接使用,则存在一定的误差,需进一步进行修正。

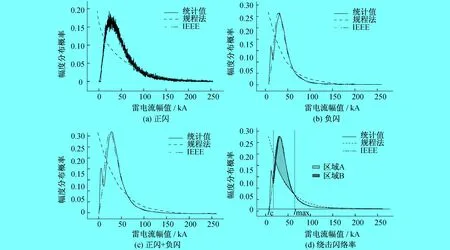
图2 概率密度分布情况

3 基于IEEE推荐公式的误差分析及修正

采用IEEE形式拟合的公式,幅值累积概率差值随着雷电流幅值的增大而变小,但其相对误差却呈指数形式增长。为进一步分析IEEE推荐公式,将雷电流幅值累积频率IEEE推荐公式与实际值之间的相对误差δ定义为

(3)

总闪及负极性闪电、正极性闪电对应的拟合公式分别以雷电流幅值200 kA、150 kA为界,之前其相对误差较小,在10%以内,之后均呈指数形式增长。因此,其适用范围存在一定的局限性,需对拟合的曲线进一步优化,故提出相应的修正公式。

设相对误差δ为f(i),即关于雷电流幅值的函数,亦称修正函数;统计值为经修正后的推荐公式P,原IEEE推荐公式为P′,则

(5)

误差对比如图3所示。由图3可以看出,误差曲线与反的单指数衰减函数相似,故设修正函数f(i)=ae(-i/b)+c。拟合修正函数参数如表2所示。

表2 拟合修正函数参数

类型abcA2正闪+负闪8．90E⁃06-21．190．06170．9702负闪1．06E⁃0521．390．05010．9769正闪7．14E⁃04-32．760．04830．9947

修正函数的拟合优度A2均可达到0.95以上,能够很好地反映误差变化情况。修正后的曲线在幅值分布范围可延伸至250 kA左右,有效降低了平均相对误差,总闪、正闪、负闪原累积频率分别由12.40%、18.66%、12.41%降为3.41%、1.91%、3.16%。

4 结 语

本文采用贵州省近9年闪电监测数据,通过拟合规程推荐、IEEE推荐两种形式,从累积概率、概率密度分布作比较,得到如下:

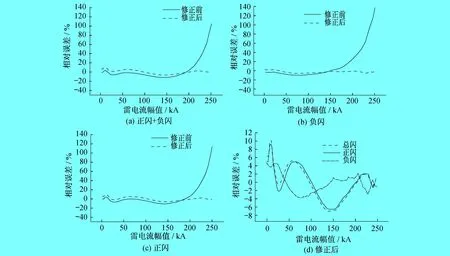
图3 误差对比

(1) 闪电幅值累积负闪较正闪集中,幅值高密度区均集中在25 kA左右。闪电极性主要以负闪为主,占总闪96%以上;正闪平均幅值强度高于负闪,达53.50 kA。

(2) 规程形式拟合的概率密度曲线与真实情况差别较大,IEEE推荐形式的公式比规程形式更接近真实情况。国内若直接采用规程中lgPI=-I/88进行相关工程计算,产生的误差会更大,建议在DL/ T620—1997中对该公式进行修订。

(3) 采用IEEE形式拟合的公式,幅值累积概率差值随着雷电流幅值的增大而变小,但其相对误差却呈指数形式增长。将相对误差作为修正函数代入IEEE拟合公式,得到新拟合公式的相对误差在5%以内,适用范围可放宽至250 kA,可很好地应用于工程计算。

[1] 电力设备过电压保护设计技术规程:SDJ 7—1979[S].

[2] 孙萍.220 kV新杭线雷电流幅值实测结果的统计分析[J].中国电力,2000,33(3):72-75.

[3] 交流电气装置的过电压保护和绝缘配合:DL/T 620—1997[S].

[4] SHIM E B,WOO J W,HAN S O,et al.Lightning characteristics in Korea and lightning performance of power systems[C]∥Proceedings of the IEEE/PES,2002:534-539.

[5] JAMES T W,WILLIAM A C.Estimating lightning performance of transmission lines Ⅱ — updates to analytical models[J].IEEE Transactions on Power Delivery,1993,8(3):1254-1267.

[6] IEEE guide for improving the lightning performance of transmission lines:IEEE Std 1243—1997[S].

[7] 王巨丰,齐冲,车治颖,等.雷电流最大陡度及幅值的频率分布[J].中国电机工程学报,2007,27(3):106-109.

[8] 李家启,王劲松,廖瑞金,等.重庆库区地貌1999—2008雷电流幅值频率分布特征[J].高电压技术,2011(5):1123-1128.

[9] 陈家宏,童雪芳,谷山强,等.雷电定位系统测量的雷电流幅值分布特征[J].高电压技术,2008(9):1893-1897.

[10] 冯志伟,肖稳安,马金福,等.基于地闪数据的雷电流幅值累积频率公式探讨[J].气象科,2012(1):137-140.

[11] 李瑞芳,吴广宁,曹晓斌,等.雷电流幅值概率计算公式[J].电工技术学报,2011(4):161-167.

Discussion for Cumulative Probability of Lightning Current Distribution Formulain in Guizhou

WU Ankun1,2, SHAO Lili1, WU Shijun1, ZHANG Shuxia1

(1 Guizhou Meteorological Disaster Prevection Technology Center, Guiyang 550081, China; 2.College of Atmospheric Sciences, Chengdu University of Information Technology, Chengdu 610225, China)

Based on the characteristics of the lightning current amplitude probability distribution in the IEEE working group and the domestic electric power industry regulation,two kinds of amplitude distribution formula of IEEE and regulation were presented.Two kinds of distribution formula were fitted by the lightning real-time monitoring data in Guizhou province,and the cumulative probability and probability density were analyzed.The results show that the cumulative probability curve of lightning current amplitude in IEEE distribution is more close to the real situation,and the probability density cuve has the larger differences between the regulation and the real situation.If the formula is used in the practice,the error will be greater.Through the further correction of fitting IEEE distributed formula,the more suitable probability distribution formula of lightning current amplitude is put forward.

lightning current amplitude; cumulative probability; probability density; relative error

吴安坤(1986—),男,工程师,从事雷电与防护方面的工作。

TU 856

B

1674-8417(2016)11-0008-05

10.16618/j.cnki.1674-8417.2016.11.003

2016-08-10

邵莉丽(1981—),女,工程师,从事雷电防御工作。

吴仕军(1980—),男,工程师,从事防雷检测等相关技术服务工作。