数形结合思想在波的干涉问题分析中的应用

许冬保● 朱文惠●

江西省九江市庐山区第一中学(332000) 江西省九江市第一中学( 332000)



数形结合思想在波的干涉问题分析中的应用

许冬保● 朱文惠●

江西省九江市庐山区第一中学(332000) 江西省九江市第一中学( 332000)

《考试大纲》关于波的干涉的要求较低，只要求了解或知道．但是高考命题已超越了考纲的约定，定量计算的问题频频出现，本文以波的干涉图样为载体，依据数形结合思想，以数解形，以形助数，从而有效解决波的干涉问题．

波的干涉；干涉图样；数形结合；以数解形；以形助数

机械波的干涉(以下简称波的干涉)在《考试大纲》中的要求是，知道其内容及含义，并能在有关问题中识别和直接使用．然而，在高考命题中，波的干涉的考查，其要求远远超越考纲的约定．关于干涉的定量计算也时常出现在试题中．本文依据数形结合思想，例谈突破波的干涉问题的有效策略．

一、数形结合，深层理解干涉图样

数形结合思想，其实质是将抽象的数学语言与直观的图像结合起来，其关键是代数问题与图形之间的相互转化，它可以使几何问题代数化，代数问题几何化．包含以数解形和以形助数两个方面．

波的干涉是指，频率相同的两列波叠加时，某些区域的振幅加大，某些区域的振幅减小．这种现象叫做波的干涉．形成的图样叫做干涉图样．

二、以数解形，准确绘制干涉图样

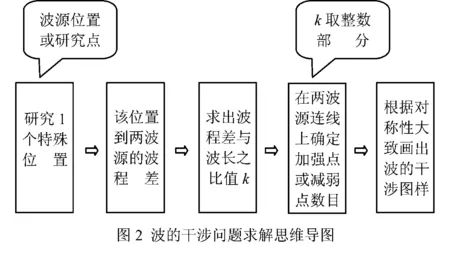
产生稳定的干涉现象必须满足一定的条件，那就是：两个波源必须是频率相同、相位差恒定、振动方向相同．这样的波源叫做相干波源，这个条件称为相干条件，它们所发出的波叫做相干波．只有两相干波叠加时，才能得到稳定的干涉图样．由图1可知，干涉图样对两波源连线及中垂线均呈现几何对称性．那么，如何绘制波的干涉图样？依据数形结合思想，以数解形，以定量分析为前提，可方便绘制波的干涉图样．绘图时，关键在于确定两波源连线上共有几处振动加强点或振动减弱点，亦即两波源之间分布多少个波长(整数倍)或多少个半波长(奇数倍)．而两波源连线之中点，对于两个同相波源，一定是振动加强点(反相波源，则为振动减弱点)．画干涉图样时，只需要画出连线中点至某一波源之间的双曲线，再根据对称性完成另一半双曲线即可．梳理绘制波的干涉图样的思维过程，形成如图2所示的思维导图．

三、以形助数，有效解决干涉问题

如何根据干涉图样解决有关干涉的问题呢？依据数形结合思想，以形助数，以干涉图样为载体，确定双曲线的分布条数(即上文中n的取值)，可以定性甚至定量解决有关问题．

1．波源连线上干涉加强或减弱区次数的确定

例1 (2013年全国大纲卷理综试题)在学校运动场上50m直跑道的两端，分别安装了由同一信号发生器带动的两个相同的扬声器．两个扬声器连续发出波长为5m的声波．一同学从该跑道的中点出发，向某一端点缓慢行进10m．在此过程中，他听到的扬声器声音由强变弱的次数为( ).

A．2 B．4 C．6 D．8

分析 两个相同的扬声器发出的声波为相干波，在空间叠加，产生稳定的干涉现象．在跑道中点位置，波程差为零，n=0；某同学向某一端点(向左或向右)行进10m，波程差等于20m，恰为4个波长，即离中点沿波源连线行进10m处为振动加强点，且n=4．由此可知其间还有对应n=1、n=2及n=3的位置．图3为声波干涉图样(示意图)，由图3可知，某同学总共能听到4次扬声器声音由强变弱．正确选项为B．

点评 传统解法是通过计算波程差得到答案．设该同学在某点处，听到加强音，该点到连线中点之距离为x，则波程差Δ=2x=nλ，式中为 整数．显然，某同学向任一端点缓慢行进10m，含跑道中点，则对应的x值分别为0、2.5m、5.0m、7.5m、10m．可见，数形结合，以数解形，以形助数，较传统解法，形象直观、简洁明了．

2．波源连线垂直方向上干涉加强或减弱区次数的确定

例2 如图4所示，MN为水池的边缘，S1、S2是池中水面上两个振动情况完全相同的波源，它们激起的水波波长为2m，S1、S2连线垂直于MN，且与MN分别相距8m和3m，设MN足够长，则在MN上水面是平静的位置数为( ).

A．1处 B．3处 C．5处 D．无数多处

分析 考查波源S2，波程差为5m，为波长的2.5倍，取n=2，而两波源连线中点，波程差为0，n=0．于是，可以粗略画出图5所示的水波的干涉图样．注意到振动加强与振动减弱区域相互间隔，在MN上的P0点为减弱区，可认为双曲线退化为直线的特殊情形．由图可知，在MN上水面平静的处数为5，选项C正确．

点评 传统解法过程如下，如图6所示，水面上平静处的波程差应为半波长的奇数倍，在MN上任取一点P(或 )，连接PS1，PS2，由几何知识可知PS1-PS2≤S1S2=5m，所以(PS1-PS2)可以取1m、3m或5m．取5m时即对应图中的P0点，取1m、3m时，左、右可分别取对称点，考察MN连线，共有5处水面是平静的．可见根据干涉图样的直观性分析，极大地简化了解题过程，提高了思维品质．

3．波源连线外圆周上干涉加强或减弱区次数的确定

例3 如图7所示，广场上有一个半径为45m的圆，AB是直径，在圆心O点和A点处分别安装两个有相同声源的扬声器，它们发出的声波的波长是10m，有一人站在B处几乎听不到声音，他沿着圆周逆时针向A走，在走到A之前，他还有几处几乎听不到声音？

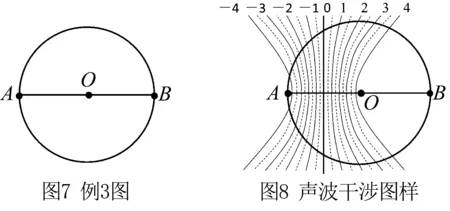
分析 考察圆心O点，波程差为波长的4.5倍，取n=4，画出AO之间声波的干涉图样，图中虚线为干涉减弱区域，如图8所示(图中数字与振动加强区相对应)．观察干涉图样与圆周的交点可知，人沿着圆周逆时针向A走，在走到A之前，共有8处几乎听不到声音．

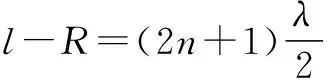
4．波源连线上干涉加强或减弱区位置坐标的确定

例4 波源S1和S2振动方向相同，频率均为4Hz，分别置于均匀介质中x轴上的O、A两点处，OA=2m，如图9所示．两波源产生的简谐横波沿 轴相向传播，波速为4m/s．己知两波源振动的初始相位相同．求OA间合振动振幅最小的点的位置．

由于OA=2m，恰为波长的2倍．由此画出图10所示的波的干涉图样(图中数字与振动加强区相对应)，在O、A两点之间振动加强与振动减弱区域的分布是均匀的，由对称性可以得到，OA间合振动振幅最小的点的位置分别为x=0.25m，0.75m，1.25m，1.75m．

综上，以波的干涉图样为载体求解波的干涉问题，能有效地提高思维的品质，促进形象思维与抽象思维的融合，利于推理能力及分析综合能力的提高．

[1]陈志风．渗透的思想，孕育的是策略．数学教学通迅(初等教育)[J]． 2013：35-37．

[2]人民教育出版社．普通高中课程标准实验教科书，物理选修3-4 [M]．北京：人民教育出版社，2010：33-35．

[3]沈克琦．高中物理①(力学)[M]．安徽：中国科学技术大学出版社，2015：215.

G632

B

1008-0333(2016)28-0056-02

中国教育学会物理教学专业委员会2013年-2016年全国物理教育科研重点课题：习题教学与物理科学方法教育的研究．