小题以大做 思维得发散——如何求异面直线所成的角

杨 虎 赵永全●

甘肃省礼县职业中等专业学校(742200)



小题以大做 思维得发散
——如何求异面直线所成的角

杨 虎 赵永全●

甘肃省礼县职业中等专业学校(742200)

在平时的教学中，有这样一些“小”题目，文字叙述少，题干短小，言简意赅，但内涵隽永，意味深邃.对这类题目进行深层次挖掘，多角度探索，会发现解法多变而灵活，对训练学生的发散思维有很大的帮助.本文就从学生资料中的一道求异面直线所成的角的小题——“小题大做”，来体会如何求异面直线所成的角.

一、题目再现

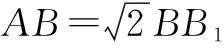
异面直线所成的角，是由空间一点分别引它们的平行线所成的锐角(或直角)来定义的.因此，在教学中要求异面直线所成的角时通常要引导学生，通过平移直线形成角，进而在某个平面中得到异面直线所成角；或者利用三垂线定理进行线线之间的转化来解决问题.

随着新课改的深入，新教材(特别是人教B版)对立体几何的处理有了一些新的变化，淡化了对学生作图能力的要求，特别是引进了空间向量的方法(实际上是把空间问题代数化)，避开了一些繁杂的作图，其中在求异面直线所成的角中运用空间向量的方法有很大的优点.即建立空间直角坐标系，利用向量的代数运算及几何性质求解.下面就这道小题，从平移、利用三垂线定理以及向量法等角度进行探索求解.

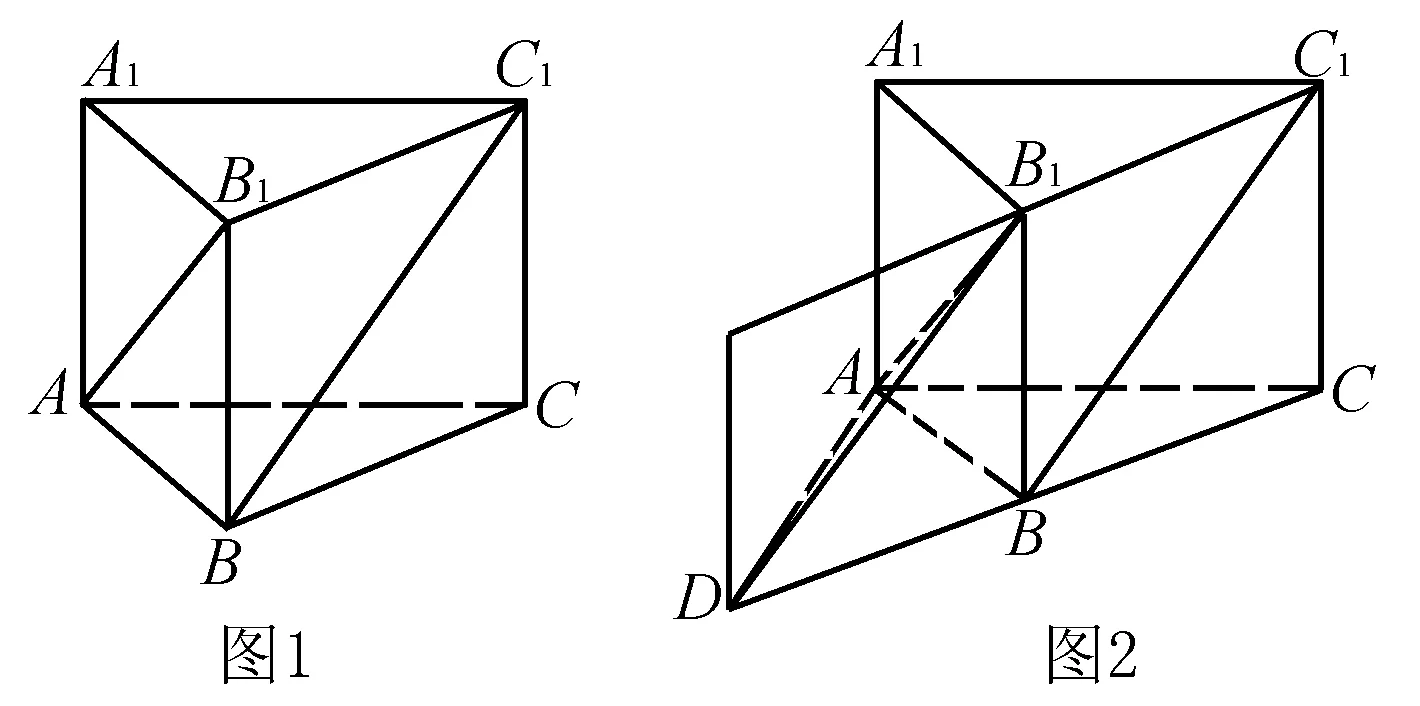
二、解法探索

思路一：利用平移转化

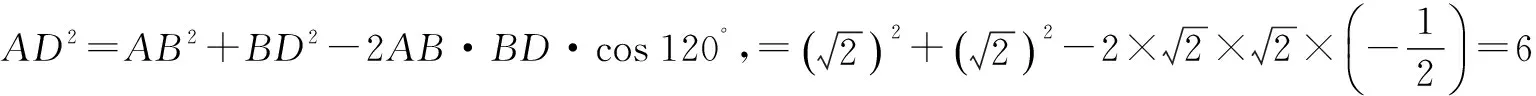
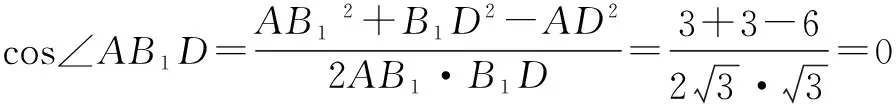
于是∠AB1D=90°.

则异面直线AB1与BC1所成的角是90°.

点评 观察直线AB1与BC1的位置，将BC1平移，即过点B1作B1D∥C1B交CB的延长线于点D，即可得到异面直线AB1与BC1所成的角.

解法2 如图3，取B1B的中点E，过点E作ME∥AB1，NE∥BC1，则M,N分别是AB,B1C1的中点，取BC的中点D，连接MD,ND，于是，∠MEN即为AB1与BC1所成的角.

于是cos∠MEN

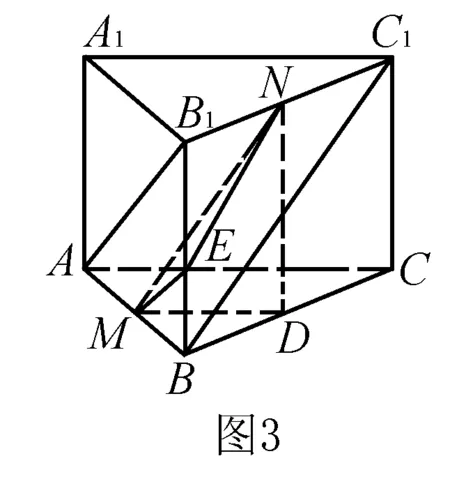
于是∠MEN=90°.

则异面直线AB1与BC1所成的角是90°.

点评 取B1B的中点E，将直线AB1与BC1平移到E处，即可得到异面直线AB1与BC1所成的角.

思路二：利用三垂线定理

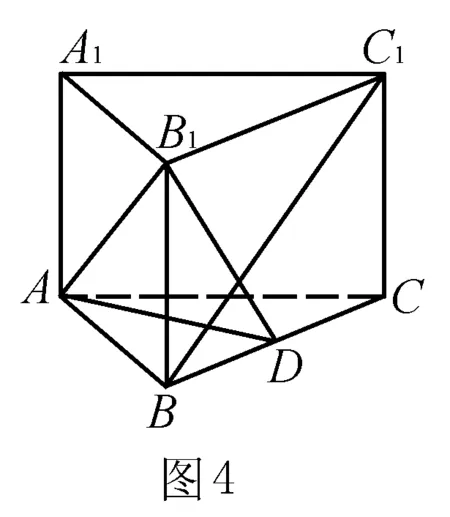
解法3 如图4，取BC的中点D，连接AB1,B1D， 由正三棱柱ABC-A1B1C1知，AD⊥BC，于是AD⊥平面BB1C1C.

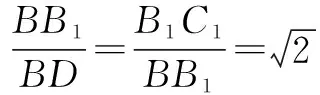
又因为B1D为A1B在面BCC1B1内的射影，所以AB1⊥BC1.

于是异面直线AB1与BC1所成的角是90°.

点评 从AB1是平面BB1C1C的斜线入手，寻找AB1在平面内的射影与BC1的关系，由三垂线定理证明异面直线垂直.

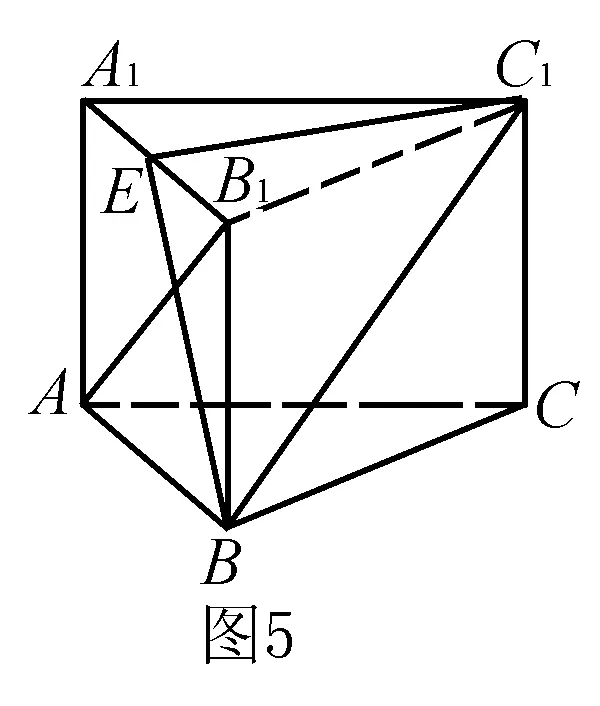
解法4 如图5，取A1B1的中点E，连接C1E,BE，由正三棱柱ABC-A1B1C1知，C1E⊥平面A1B1BA.

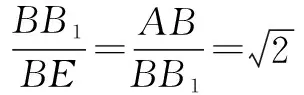
于是异面直线AB1与BC1所成的角是90°.

点评 本解法与解法3相似，只是所选取的斜线

▶

▶与平面不同而已.

思路三：利用向量

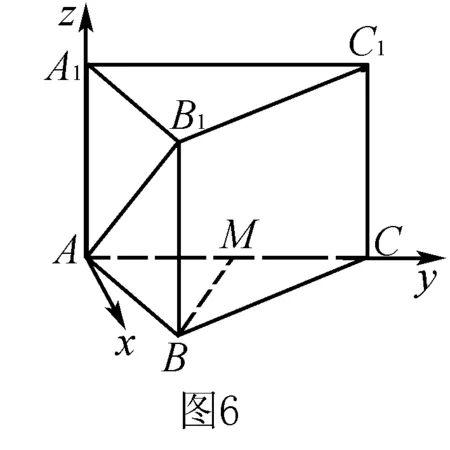
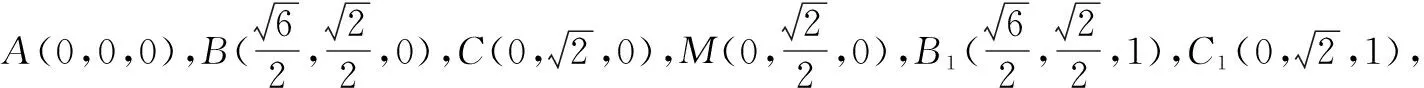
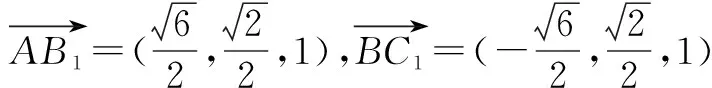
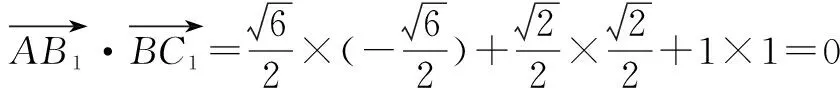
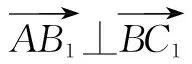
点评：通过建立空间直角坐标系，把向量用坐标形式来表示，通过计算向量的数量积，便可知其异面直线AB1与BC1垂直.

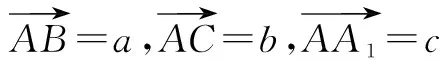
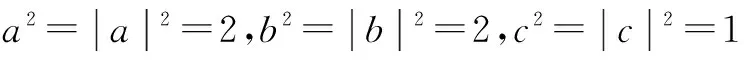
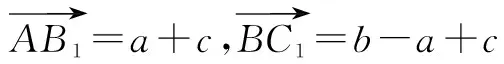
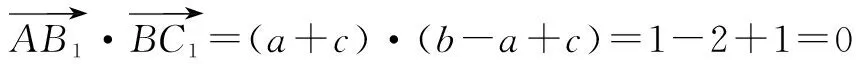
于是异面直线AB1与BC1所成的角是90°.

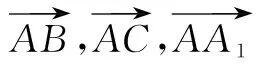
三、解后反思

通过对这道小题的探索发现，从不同的角度看待问题会有不同的求解方法，这对培养学生的发散思维是有益的.在本题解法中，思路一与思路二要求学生有良好的作图能力，且能够在作图后在所需要的三角形中计算出各条线段的长度，从而达到求解目的.而思路三只需建立空间直角坐标系，标出相应的点的坐标，从而得到所需向量的坐标，来求出两个向量的夹角，即所求的两条直线所成的角.另外，对异面直线所成的角的求法我们还可以借用一些固定的模型，引用一些已知的公式来求出角的大小.

G632

B

1008-0333(2016)28-0008-02