倾斜角互补的几种表现形式

苏艺伟●

福建省龙海第一中学新校区(363100)



倾斜角互补的几种表现形式

苏艺伟●

福建省龙海第一中学新校区(363100)

人教A版必修二第3.1.1节介绍了直线的倾斜角与斜率.在本节的学习中我们知道了一个知识点:若两条直线倾斜角互补,且斜率都存在,则斜率之和为零.这是一个再平常不过的基础知识,以至于没能引起同学甚至教师足够的重视.事实上,在重要的考试当中经常会涉及到这个知识点的运用,而题目往往不会直接给出“倾斜角互补”这么明显的条件,而是变换另外的表现形式.这个时候就需要将其进行转化,再利用该知识点来解决问题.本文着重探讨了“倾斜角互补”的几种常见表现形式,以期能够对教学解题起到较好的指导作用.

一、入射光线和反射光线

设l1为入射光线,经过x轴反射后,l2为反射光线,此时两直线倾斜角互补.

例1 光线沿直线x+2y-1=0射入,经过x轴反射,求反射光线所在的直线方程.

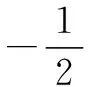
二、关于x轴对称(x轴是角平分线)

如果两条直线关于x轴对称,显然两直线的倾斜角是互补的.如果x轴是某一个角的角平分线,那么这个角的两边所在直线必定关于x轴对称,故倾斜角也是互补的.

例2 教材复习参考题B组第1题

与直线3x-4y+5=0关于x轴对称的直线的方程为( ).

A.3x+4y-5=0 B.3x+4y+5=0

C.3x-4y+5=0 D. 3x-4y-5=0

例3 (2013年陕西高考理科第20题)

已知动圆过定点A(4,0),且在y轴上截得的弦MN的长为8.

(1)求动圆圆心的轨迹C的方程；

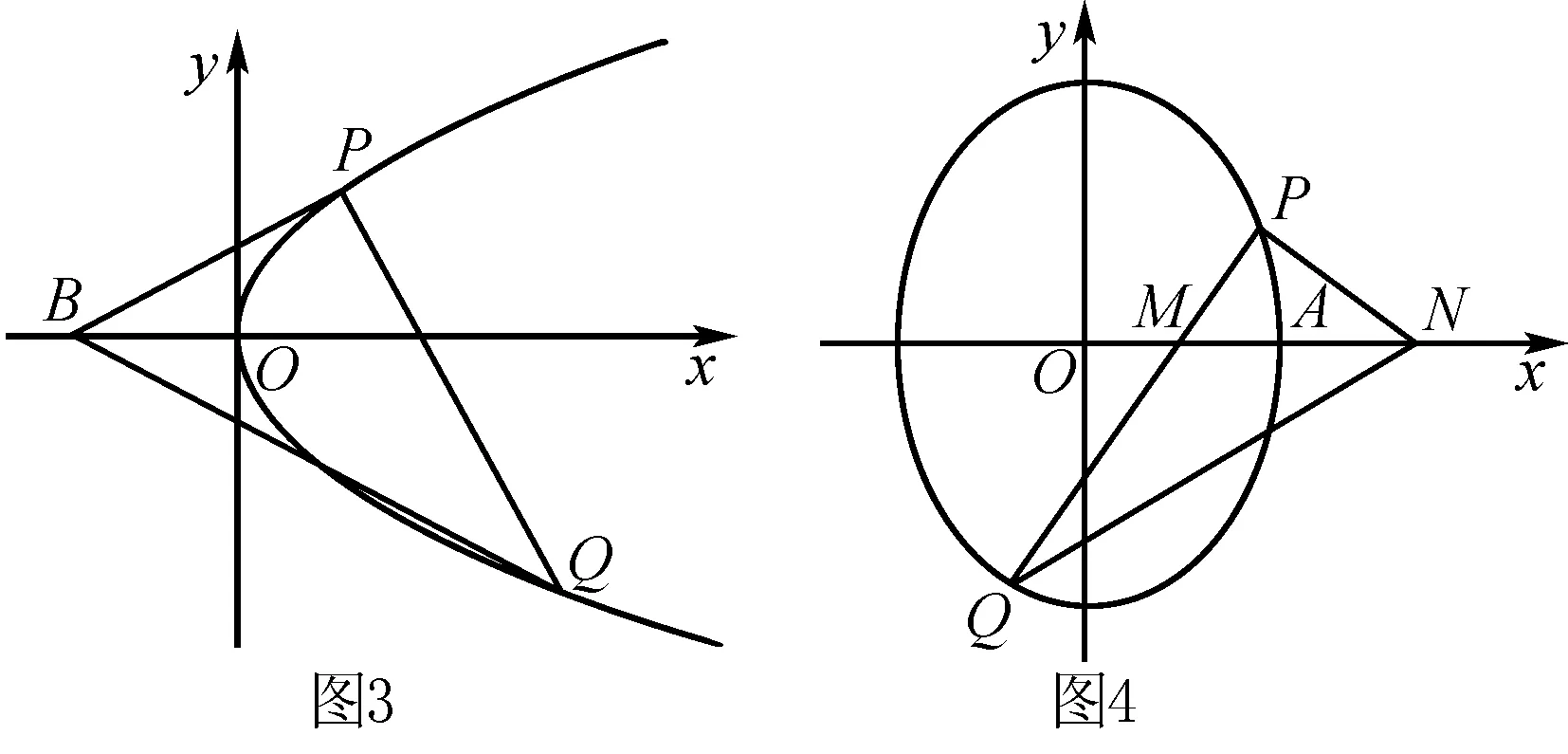
(2)已知点B(-1,0),设不垂直于x轴的直线l与轨迹C交于不同的两点P,Q,若x轴是∠PBQ的角平分线,证明直线l过定点.

解析 (1)易求得轨迹C的方程为y2=8x.

(2)如图(3)所示,设直线l方程为y=kx+b,P(x1,kx1+b),Q(x2,kx2+b).

因为x轴是∠PBQ的角平分线,故直线PB,QB倾斜角互补,kPB+kPQ=0.

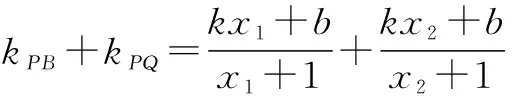
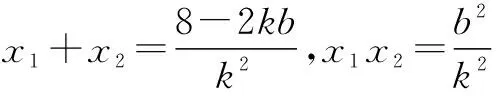
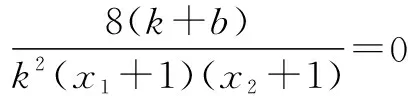
三、某两个角相等(两条线段相等)

如果题目条件为某两个角相等,则往往隐含了相应的两条直线倾斜角互补.有时候题目会以某个三角形中某两条线段相等为条件,此时也可以转化为相应的两条直线倾斜角互补.

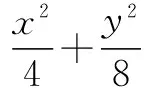
(2)假设存在N(x0,0)满足题意.

当PQ⊥x轴时,由椭圆的对称性可知,恒有∠PNM=∠QNM,即x0∈R.

当PQ与x轴不垂直时,设直线PQ方程为y=k(x-1),P(x1,k(x1-1)),Q(x2,k(x2-1)).

因为∠PNM=∠QNM,故直线PN,QN倾斜角互补,kPN+kQN=0.

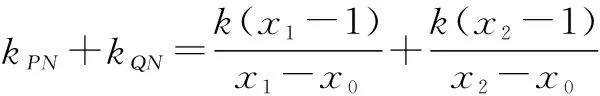
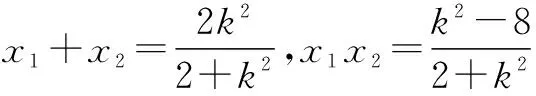
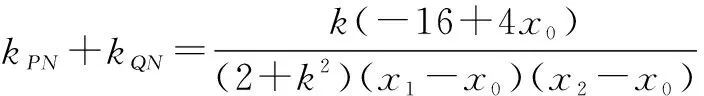
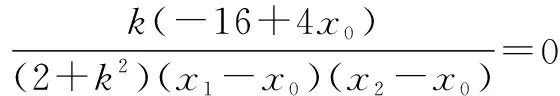
综上,在x轴上存在定点N(4,0),使得∠PNM=∠QNM.

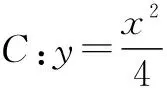
解析 假设存在符合题意的点P(0,t),设M(x1,kx1+a),N(x2,kx2+a).

因为∠OPM=∠OPN,故直线PM,PN倾斜角互补,kPM+kPN=0.

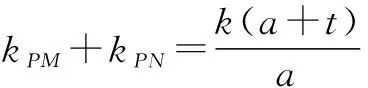
要使当k变动时,总有∠OPM=∠PON,则t=-a.

因此存在符合题意的点P(0,-a).

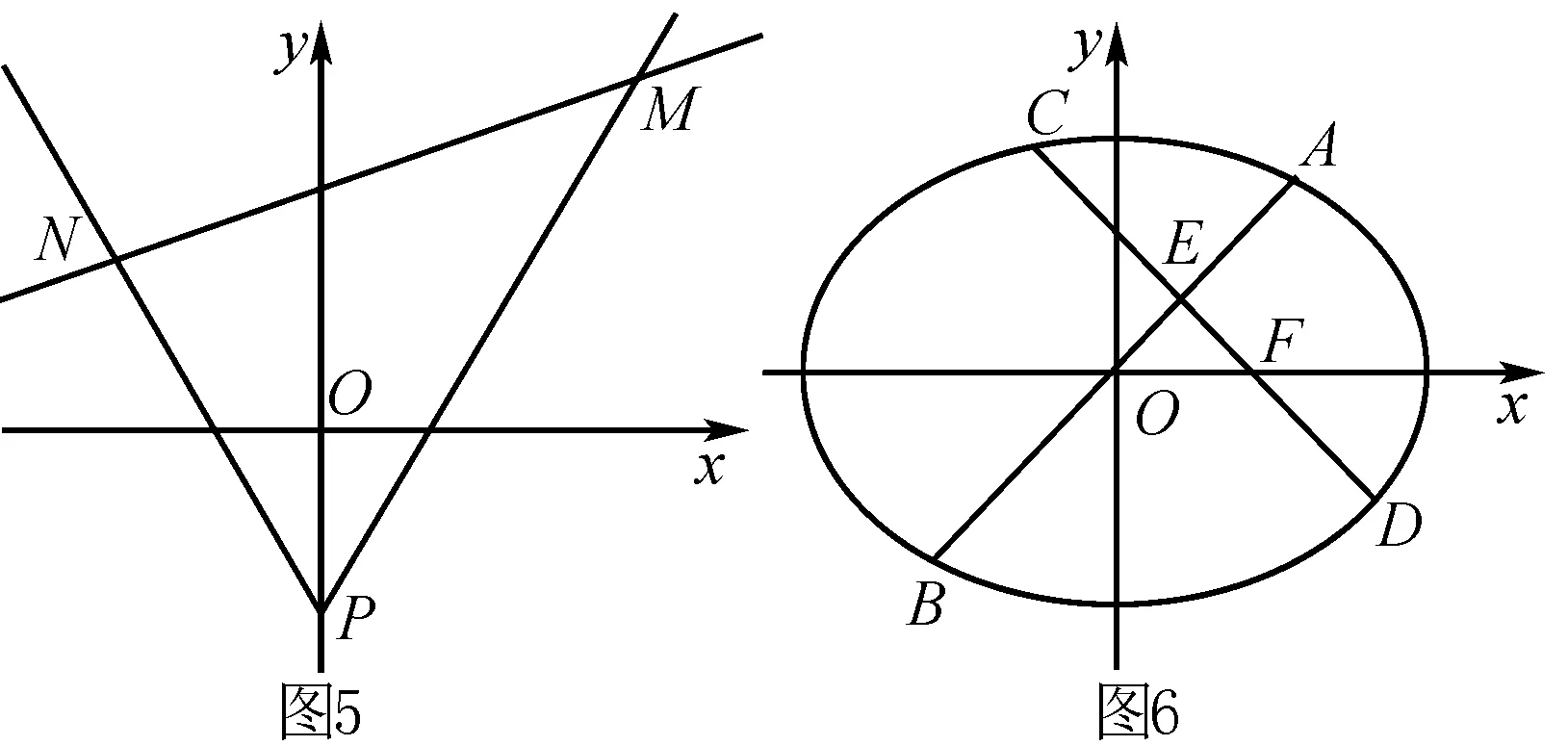
解析 由OE=EF得直线AB,CD的倾斜角互补,斜率互为相反数.

设直线AB的方程为y=kx,直线CD的方程为y=-k(x-1).

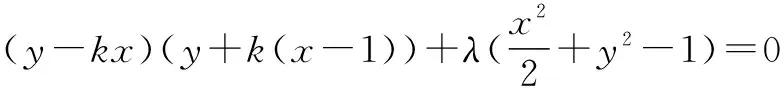
显然直线AC,BD也在上述二次曲线方程中.

设AC:A1x+B1y+C1=0,BD:A2x+B2y+C2=0.

由(A1x+B1y+C1)(A2x+B2y+C2)=0,展开得

A1A2x2+B1B2y2+(A1B2+B1A2)xy+(A1C2+C1A2)x+(B1C2+C1B2)y+C2C1=0…(2)

比较(1),(2)两式,xy项系数为0,故A1B2+B1A2=0.

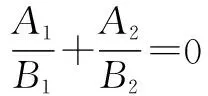
因此直线AC,BD的斜率之和为定值0.

同一个知识点可以有不同的表现形式,在实际解题中我们要善于引导学生透过表现抓住问题的本质.这样不仅能够丰富解题经验,还能形成良好的逻辑思维能力,提升思辨智慧.

G632

B

1008-0333(2016)28-0037-02