求轨迹问题之“内功心法”

乌鲁木齐市第一中学(830002)

虞建友●



求轨迹问题之“内功心法”

乌鲁木齐市第一中学(830002)

虞建友●

求轨迹问题是高中数学解析几何的热点问题，于是被总结出了诸如“直接法、代入法、定义法、参数法、交轨法”等名称好记，操作有套路的方法.但是学生在遇到问题时，选择用什么方法呢？这才是问题的症结所在.本文就课本中一道练习题的解法阐述求解轨迹问题的思路——找寻运动过程中不变的关系，并将之代数表示.

例题 人教社《普通高中课程标准实验教科书数学选修2-1》第37页练习第3题：

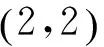
分析 求点M的轨迹方程，就要思考点M是怎么运动的.着眼于找出运动过程中不变的关系，便有不同的解法.

解法1

分析 注意到运动变化过程中，直线CA垂直于直线CB是不变的.将这种不变的关系呈现即可.

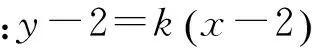
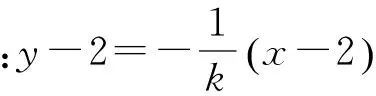
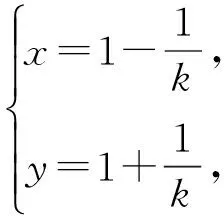
得M的轨迹方程：x+y=2 ①.

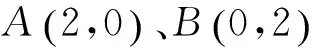
综上，点M的轨迹方程：x+y=2 (这就是所谓的“参数法”).

解法2

分析：依然抓住运动变化过程中，直线CA垂直于直线CB是不变的这一关系，换一种呈现方式.

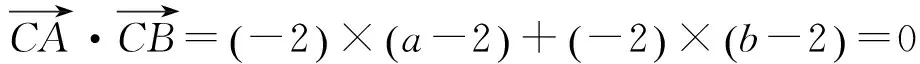
解法3

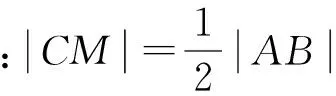
注：解法1、2的着眼点一致，思维量不是很大，但是运算量不小.方法不一样在于呈现两直线互相垂直的方式不一样.解法3也是着眼于呈现运动过程中不变的关系，思维量大，但是运算小.这正是数学的魅力，殊途同归，因人而异，每个人都能学到适合自己的数学.想得多，算的就少.想得少，算的就多.但是无论哪种方法，都用了“内功心法”： 将运动过程中不变的关系呈现出来.解析几何的本质是用代数的方法解决几何问题，而轨迹问题就是将运动规律代数化，辩证唯物主义说运动和静止是对立的统一的，所以找运动规律就是要“动中找静”.这也是数学的哲学性的体现.

牛刀小试，一招“毙敌”

分析：只需抓住运动变化过程中，“杆的中点到坐标原点的距离等于杆长的一半”这一不变关系即可.

G632

B

1008-0333(2016)31-0025-01