以求点轨迹方程为例探究高中数学解题中对九项循证策略的有效应用
福建省泉州市晋江市磁灶中学(362214)
汪水勇●
以求点轨迹方程为例探究高中数学解题中对九项循证策略的有效应用
福建省泉州市晋江市磁灶中学(362214)
汪水勇●
九项循证策略在高中数学教学中具有重要的运用价值,能能够有效地提高学习效果、效率及效益,实现教学的有效性.本文以高中数学“求点轨迹方程” 教学为例,探究高中数学解题中对九项循证策略的有效应用.
高中数学;轨迹方程;九项循征策略
九项循证策略是在2001年形成的一个十分独特的理论,该理论的成熟时间在2012年,该理论体系还是比较年轻的.最早将该理论提出的是美国中部教育研究和学习实验室的多年试验成果.
一、九项循证策略的意义
九项循证策略的主要九项关系分别是:第一是目标及反馈,二是努力及认可,三是合作学习,四是线索,问题及先行的组织者,五是非评议的表达,六是概括以及记录,七是家庭作业及练习,九是对相似问题的区别进行分辨,形成自身的想法最终验证.
二、九项循证策略在点轨迹方程教学实践中的运用
1.营造环境
教师首先需要告知学生,学生所学习的这一部分的重要目的,并且给出十分明确的学习目标,帮助学生对其中的重难点进行了解.
2.理解知识运用知识
对原有的知识进行回顾,回忆自己曾经学过的和本节课的联系相关的知识,在教材内对解题的步骤实行规范,曲线方程以及点的轨迹方程为基本的数学思想,对相应部分的练习进行增加,确保学生能够在练习中对公式进行理解并实现使用.
设计的主要策略为:在开展设计中,对渐进形式问题的提出要格外注意,通过问题给出学生理解的线索,利用问题促进学生的思考.
a.教材在推导椭圆方程中,是通过建系、设点、列出关系和代入及简化这几项基本步骤实现推导的,此外还是这节课中的基础和拓展点,尤其在设点、列关系式和代入中可能会遇到难点,在这一节课中的主要学习内容需要进行关注.
b.在△ABC中,若是A(-1,0),B(1,0),C(1,2),可以得知AB⊥BC,那么kABkBC=-1,这一说法对么?若不对,则给出理由.
c.A(-1,0),B(1,0),平面内的P到A、B两点的距离之和是2,那么P点的轨迹就是以A、B为焦点的椭圆,对不对?若是不对,则给出理由.
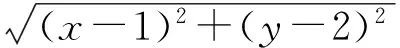
整个设计策略,线索问题及先行的组织者.详细的来说就是在一节课开始前,要采用线索、问题和先行组织者,促进学生聚焦于即将开展的学习重点上,加强学习的动机.借助问题(1)来对学生进行引导促使学生对本节课的内容实行关注,随后将推断性的问题实行提出,从而来提升学生运用原有知识的能力,激发学生的兴趣以及学习动机.
(1)直接法求出轨迹方程
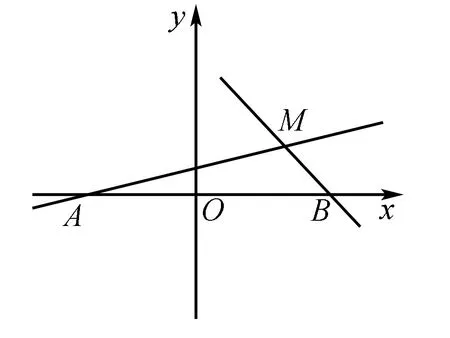
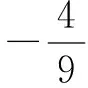
变式1 设点A、B的坐标分别是(-1,0)和(1,0).直线AM、BM相交于点M,并且它们的斜率商是2,求出点M的轨迹方程.
变式2 点P和定点F(2,0)的距离及它到定直线x=8 距离之比是1∶2,随后求出点P点轨迹方程,并且说出轨迹的图形是什么.
变式1和变式2之间的共同点在于采用直接法求出轨迹方程的基本步骤.并且变式1帮助突破了设点中的范围确定的方式这一难点.变式2处理采用直接法对步骤强化,同时还根据学生的情况选择运用椭圆的第二定义求解.
在上述的例1中可以引导学生通过在斜率下画线作为标记,并且引导学生画线的目的,引导学生对相应的概念进行联系.斜率必须存在,因此点M(x,y)的横坐标无法和A、B两点的横坐标相同,也就是x≠±5.
(2)定义法求出轨迹方程
例2 已知△ABC的周长是16,点B(-3,0),点C(3,0),求出A的轨迹方程.
变式1M为平面内的任意一个点,若M(x,y)在点的运动过程中,满足下面关系式:
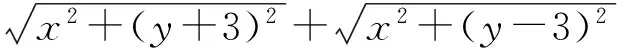
变式2 已知一定圆的方程A:(x+1)2+y2=16,其圆心是A,动圆M过点B(1,0)并且和圆A相切,动圆的圆心M的轨迹标记为C,求出曲线C的方程.
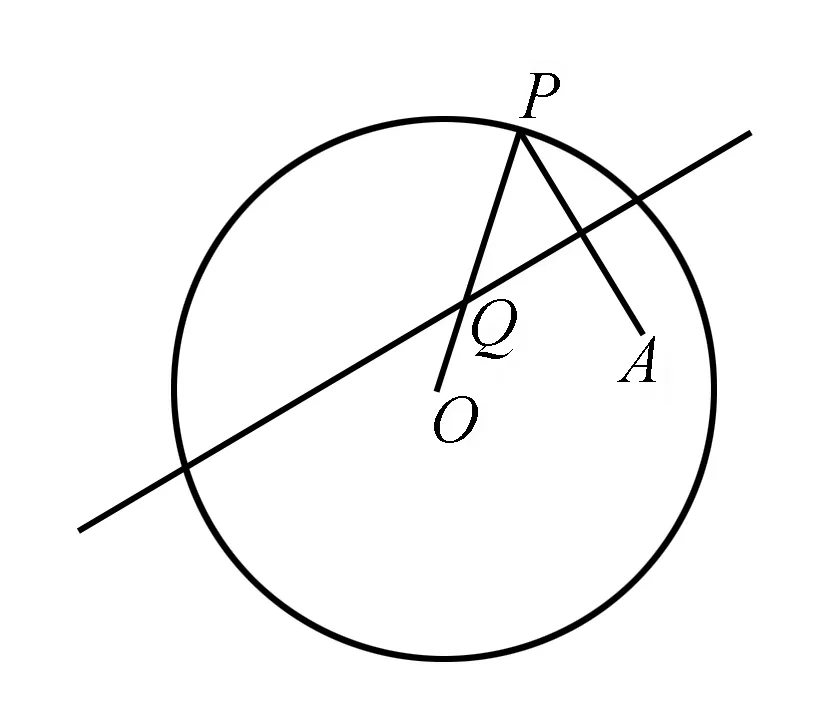
变式3 如图,圆O的半径长度是r,A是圆O中的一个定点,P属于圆上的任意一个点.线段AP的垂直平分线l与半径OP相交于点Q,当点P在圆上运动时,点Q的轨迹是什么?
设计思路 对定义法求出轨迹方程的基本步骤进行掌握.例2是定义法最为直接的体现,变式1和变式2的变化都是比较简单和直接的,可以促进学生对关系的进一步认识和巩固,变式1是对例2集合关系的代数翻译,变式1将椭圆的定义关系采用两圆相切来构建,变式3 的问题情境实行了更新,增加了思维量,目的是要对定义法的迁移使用进行促进,点Q的轨迹将会成为双曲线,为以后的课程开展打下基础.
(3)相关点对轨迹方程的求解
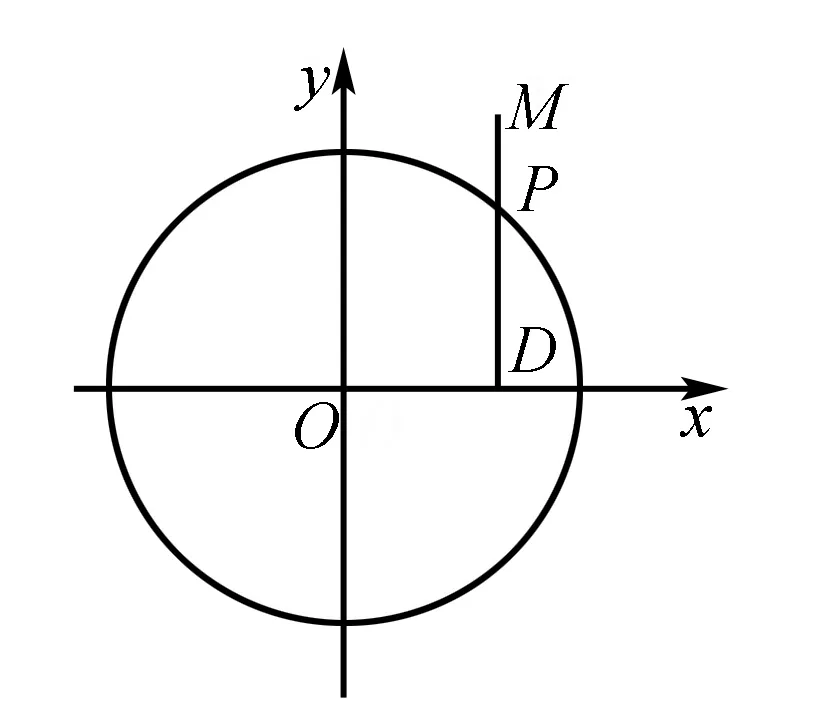
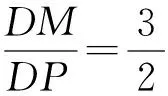
变式1 在圆x2+y2=4上任意取一点P,并且过该点做y轴垂线段PD,且D为垂足.点P在圆上运动的时候,线段PD的中点M的轨迹是什么?
变式2 在圆x2+y2=4上任意取一点P,该点关于直线y=x+1的对称点为M,点P在圆上运动时,M的轨迹是什么?
掌握相关点求出轨迹方程的基本步骤,变式1和例题比较类似,变式1是将例3中的已知点的轨迹和要求的点的轨迹做了交换,变式1就是将例3中的x轴变成了y轴.这样实现了知识运用的迁移.
三、九项循证策略在点轨迹方程解题中的运用

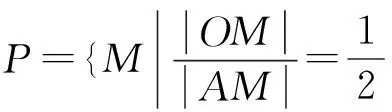
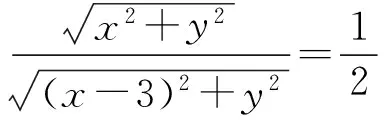
将上述式子①两边都平方后,简化得到了x2+y2+2x-3=0②.
化成标准式子后是:(x+1)2+y2=4
因而所求的方程②代表的曲线是以C(-1,0)为圆心,半径是2的圆.
点评 从题目汇总可以知到两个定点的距离比是常数的轨迹为圆(这个比不是0也不是1).在实际的练习中要记住各个曲线的特点,这样带来较大的方便.在对问题进行解答前,要对题目的解法进行判断和掌握,要确定题目的思路是比较接近哪个方向的,如此在开展更多的相似练习中就可以掌握最基本的最好的解题方法.
九项循证策略是一种十分优良且有效的教学思想,该策略是借助对学生学习产生影响的九个因素展开针对性指导,实现对学习成绩和解题能力的提升,从而提升学习质量,这对目前的高中数据教育而言是有着十分强大的指导意义的.
[1]课程教材研究所. 20 世纪中国中小学课程标准·教学大纲汇编 (历史卷)[G]. 北京: 人民教育出版社,2001.
[2]杭秀,盛群力.做循证教学研究的新范例马扎诺和迪安的有效教学九项循策略[J].课程教学研究,2013.8
G632
B
1008-0333(2016)31-0012-02

