浅析高中物理圆周运动的几种解题方法

湖南省长沙市周南中学(425600)

孙岸文●



浅析高中物理圆周运动的几种解题方法

湖南省长沙市周南中学(425600)

孙岸文●

圆周运动是指一质点以某点为圆心以r为半径所做的轨迹为圆周的一种常见的曲线运动，它虽是高一教程的内容，但是贯穿了整个高中，涉及的题目覆盖面广，综合力强，本文简单分析了一下圆周运动中不同类型题目的几种解题方法.

高中物理；圆周运动；解题方法

圆周运动涉及的知识点比较多，覆盖面也比较广，因此有关圆周运动的题目总会存在着一定的难度.

一、圆周运动题目的一般解题步骤

(1)确定要研究的对象，分析研究对象的运动状态；(2)确定圆心、轨道半径及向心加速度的方向；(3)对研究对象进行受力分析，把各方向的力都分解到半径和垂直于半径的方向上；(4)根据向心力公式和F合=F向，列牛顿第二定律方程进行求解.

二、匀速圆周运动问题

对于匀速圆周运动的题目一定要注意的是它不可能是匀变速运动，因为它在运动的过程中是速度的大小不变而速度的方向和加速度的方向是一直改变的，还有一点是物体受到的所有力的合力提供的向心力一定是指向圆心的，圆周切线方向上与垂直圆周平面方向上的合外力必定为零.

例 如图1，两根轻绳同系一质量为0.1 kg的小球，两绳另一端分别固定在A、B两点，AC长为2米，当两绳都拉直时，绳与轴的夹角分别为30°和45°，求小球做匀速圆周运动角速度ω为4rad/s时，上下两绳各自的拉力？

图1

解析 两绳逐渐张紧的过程中，小球受的力从0慢慢增大.

①BC刚好被拉直时，T2为0，设AC上的拉力为T1，此时角速度为ω1，要使BC有拉力，ω应大于ω1，对小球受力分析：半径方向上T1sin30°=mω12LABsin30°

垂直半径的方向上T1cos30°=mg

②AC刚好被拉直时，T1为0 ，设BC上的拉力为T2，

此时角速度为ω2，要使AC有拉力，ω应小于ω2，对

小球受力分析：

半径方向上T2sin45° =mω22LACsin30°

垂直半径的方向上T2cos45° =mg

由①②求得ω1=2.4rad/s，ω2= 3.14rad/s，因为ω>ω2，所以此时AC已无拉力，BC与轴的夹角大于45°，对小球受力分析：

半径方向上T2cosθ=mω2LBCsinθ

垂直半径的方向上T2cosθ=mg

又有LACsin30° =LBCsin45°

最终求得T1，T2的大小.

三、竖直面内圆周运动问题

竖直面内圆周运动问题一般有三种情况，分析其运动时的受力特点：

(1)绳子拉球问题，如图2甲，弹力只可能向下，此种情况只有F+mg=(mv2) /R≥mg，小球才能通过最高点；

(2)车过桥问题，如图2中乙，弹力只可能向上，

此种情况只有mg-F=(mv2)/R≤mg，车才能

安全通过桥面，不发生危险；

图2

(3)管内转球问题，如图2中丙，弹力既可能向上也可能向下，第一种情况，①物体所受弹力向下即F+mg=(mv2)/R>mg；②物体所受弹力向上即mg-F=(mv2)/Rmg时，向心力有一个解即F+mg；③弹力F=mg时，向心力为零，此时物体恰好能通过最高点.

四、皮带传送问题

对于皮带传送的题目一定要注意的两点是在同一转轴上各点的角速度是相等的，与同一皮带相接触的各点线速度是相等的.还有，皮带传送过程中，动轮受到静摩擦力带动轮子转动，主动轮受到摩擦带动皮带运转，此时，轮子所受摩擦力的方向沿从动轮的切线与轮的转动方向相同，主动轮受到摩擦力的方向沿轮的切线与轮的转动方向相反.

例 如图3为一皮带传送装置，左轮中大轮半径为4r，小轮半径为2r，b为小轮上一点，

图3

到圆心距离为r，c、d分别为小轮和大轮的边缘上；右轮为一半径为r的小轮，a位于其边缘上，皮带传送的过程中不打滑，则

A.a、b两点线速度大小相等

B.a、c两点角速度大小相等

C.a、d两点向心加速度大小相等

D.a、b、c、d四点中，b点加速度最小

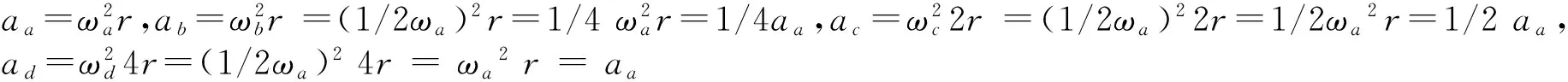
[1]王萍.浅谈极限思维法在高中物理解题中的应用[J].数理化学习，2013(11)

[2]宋敏丽.学好高中物理为成才打好基础[J].成才之路，2014年24期

[3]昌春香.高中物理在学生心中的“价值”的调查与反思[J].湖南中学物理，2014年10期

G632

B

1008-0333(2016)31-0073-01