构造数学模型妙解三角函数最值
2016-12-16 02:51江西省赣州市石城县石城中学342700
数理化解题研究 2016年22期
江西省赣州市石城县石城中学(342700)
黄天扬●
构造数学模型妙解三角函数最值
江西省赣州市石城县石城中学(342700)
黄天扬●
1.构造函数模型
利用函数在某一区间上具有单调性求最值


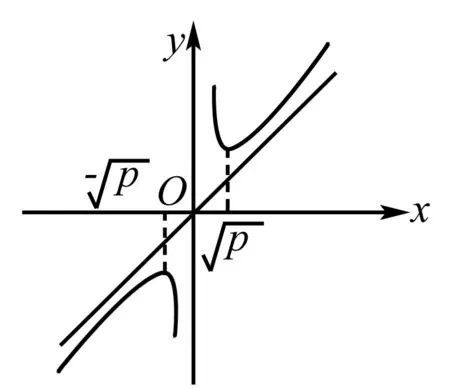


利用均值不等式等号不成立时,可化为双勾函数,应用双勾函数单调性去解决.
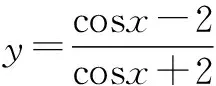
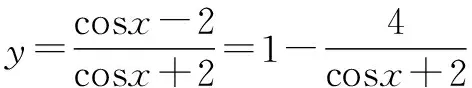
归纳 含有同名的三角函数求最值时,要有意识地将问题的结构特征与函数联系起来,构造函数模型.
2.构造均值不等式模型
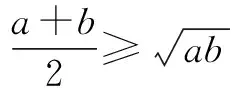



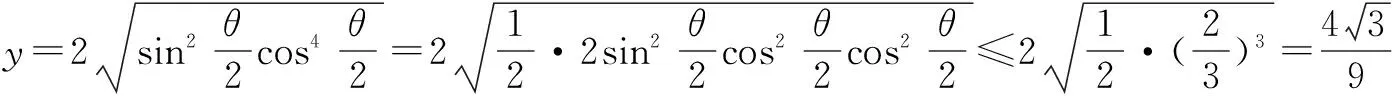
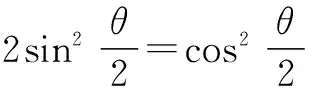
注意:利用均值不等式要观察等号成立的条件.
3.构造斜率模型
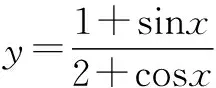
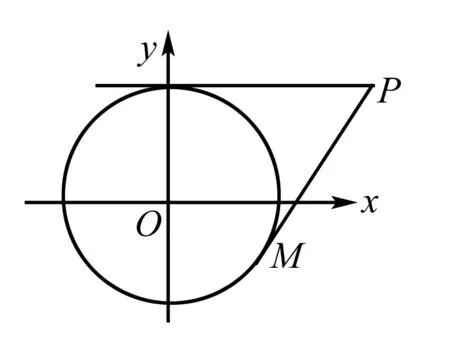

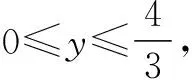
归纳:
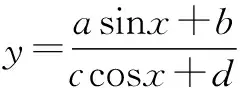
4.构造问题结构的向量模型
由数量积a·b=|a||b|cosθ, 有|a·b|≤|a||b|.
例5 求函数y=sin2x+2sinxcosx+3cos2x的最值.
解 原函数可化为y=2+sin2x+cos2x,所以只须求sin2x+cos2x的最值.设a=(sin2x,cos2x),b=(1,1).
∴|a·b|≤|a||b|,

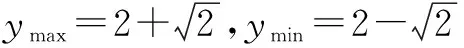
归纳 用向量解三角问题,关键在于巧妙地构造向量,为此需要我们有意识地将问题的结构特征与向量的有关运算及表示法联系起来.
总之,在求三角函数的最值中,灵活运用数学的各种方法,会使问题的解答简捷,明了.
G632
B
1008-0333(2016)22-0031-01
猜你喜欢
——赣州市审计局这样让困难群众感受温暖
审计与理财(2022年8期)2022-08-31
大众文艺(2018年24期)2018-12-20
老年教育(老年大学)(2018年10期)2018-10-24
农产品市场周刊(2017年29期)2017-10-22
宝藏(2017年7期)2017-08-09
安徽农业科学(2017年2期)2017-07-13
散文选刊·下半月(2017年1期)2017-02-22
中国社会历史评论(2016年2期)2016-06-27
环境与生活(2016年6期)2016-02-27
广州文博(2016年0期)2016-02-27

