坐标法——轻松攻克向量问题

甘肃省兰州市兰化一中(730060)

梁宗明●



坐标法
——轻松攻克向量问题

甘肃省兰州市兰化一中(730060)

梁宗明●

向量的坐标表示，实际是向量的代数表示.向量坐标的引入使向量完全代数化，将数与形紧密结合起来，就可以使很多几何问题的解答化为学生熟知的数量运算.因此，恰当地在向量问题中使用坐标法，就能够化繁为简、化难为易，轻松攻克向量问题.

建系；坐标法；代数运算；回归

平面向量问题对学生的平面几何推理与向量逻辑思维能力要求较高，在处理平面向量问题时，经常要对研究的复杂向量表达式拆分重组、配凑，尽可能靠拢已知量，依靠几何意义，寻找突破口，一旦切入不当，就会陷入复杂的运算甚至循环论证.若恰当使用向量坐标法就会避免此类麻烦的产生.而向量问题又是高考命题的热点，寻求其简易解法，显得尤为重要.本文通过具体高考题，从如何建系、确定点的坐标、运算、回归等方面，介绍向量坐标法在解决平面向量问题中的优越性.

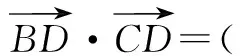
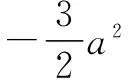
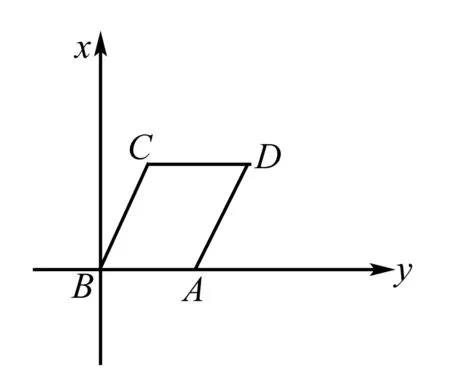
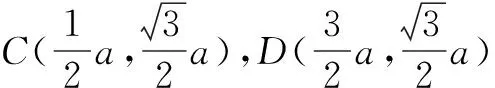
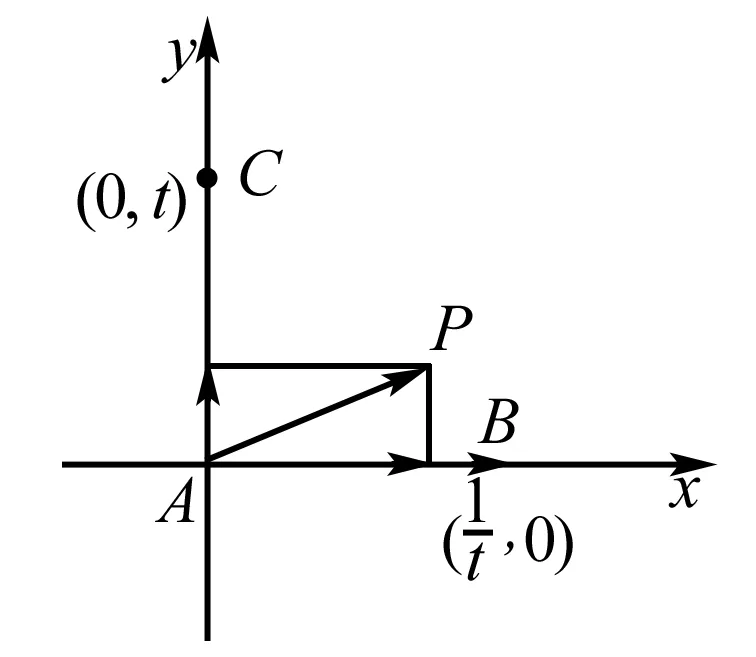
A．13 B．15 C．19 D．21

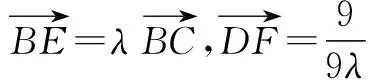
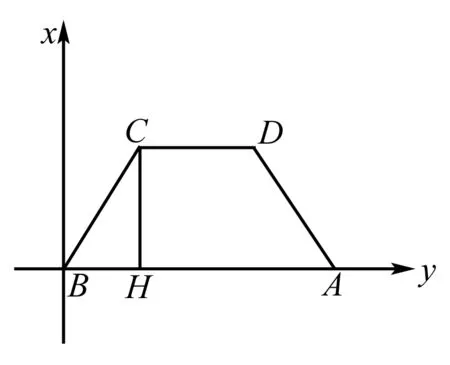
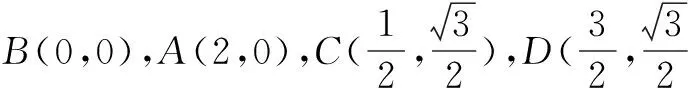
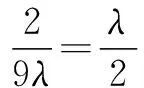
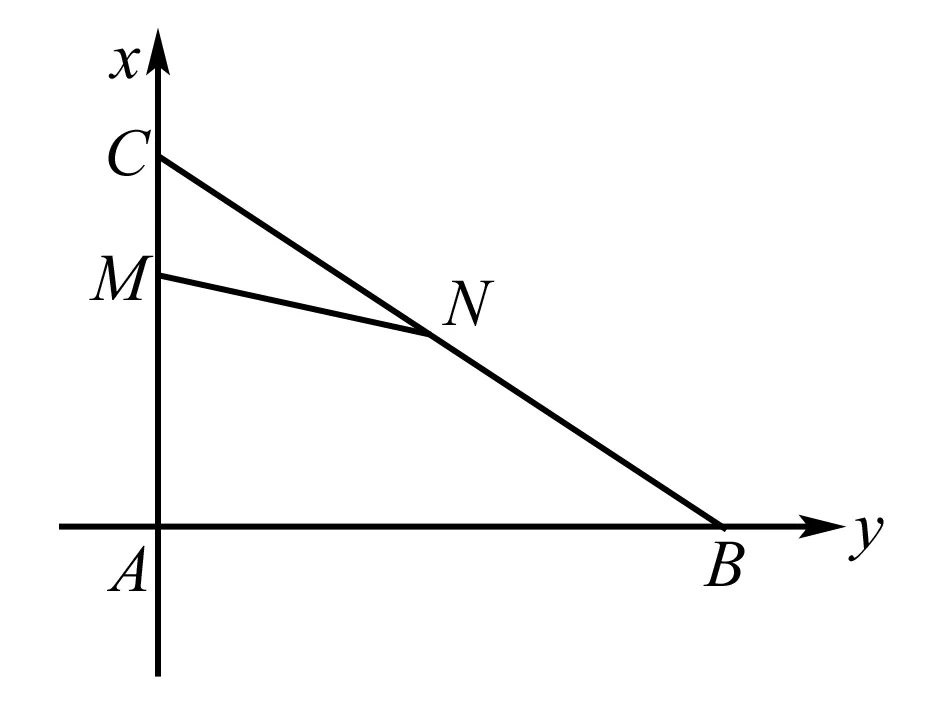
试题分析 此题没有明显建立坐标系的条件，在符合题意情况下可将其极端特殊化.

总结：在用坐标法解决向量问题时，如果有明显直角或一些特殊角存在，即可利用条件建立直角坐标系，尽可能使图形位于第一象限，这样可使点坐标尽量简洁，如若没有明显建系条件，可依据题目条件，极端特殊化一些直角出现，同时赋予线段长度，这样可以使问题大大简化，降低运算量，使问题快速、准确得以解决.

G632

B

1008-0333(2016)22-0015-01