重载焊接机器人刚度与变形分析

张小光，邓启超，许德章



重载焊接机器人刚度与变形分析

张小光，邓启超，许德章

本文对重载焊接机器人的传动系统进行分析，从其减速器、齿轮副、传动轴和伺服电机进行理论计算，求出各个传动机构的刚度。对机器人的大臂和小臂进行受力分析，求出所受力的大小。通过Simulation软件对应力变形进行了分析验证，为重载焊接机器人在性能分析和结构优化中提供理论基础。

刚度；静应力；运动学；动力学

在重载机器人设计中，刚度是一项重要的评价机器人性能指标的依据。目前，针对重载焊接机器人刚度方面的研究多数是单个部件分析或者通过建立刚度矩阵方程。重载机器人的刚度与重载机器人的尺度参数、界面参数和拓扑结构密切相关，所以细杆组成的连杆机构不一定比由粗杆组成的连杆机构的刚度要高[1]。机器人末端受到外力作用后会产生变形，其变形的大小与末端刚度和作用力的大小有关。因此，操作臂刚度的大小将影响机器人手臂的动态特性和定位精度[2]。本文通过对负载165KG重载焊接机器人各传动关节的刚度进行计算，并且利用Simulation软件进行了变形分析，从而验证了刚度与变形之间的关系，为提高机器人精度提供理论基础。

1 机器人本体刚度计算

1.1 重载焊接机器人的传动系统

重载焊接机器人各关节传动系统的传输路线如下表所示：

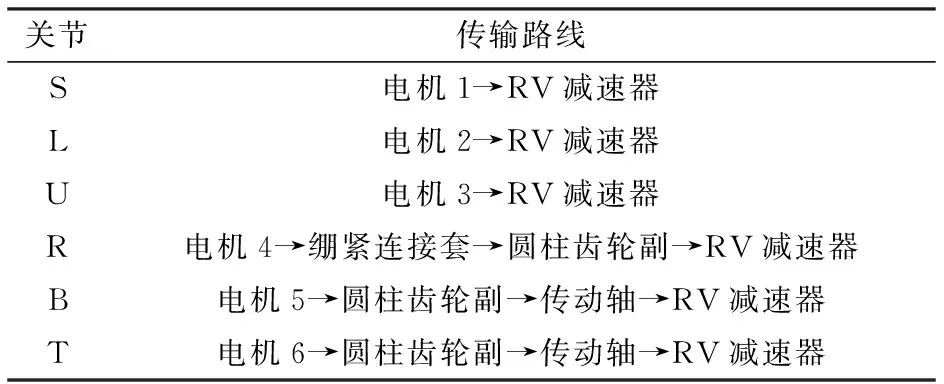
表1 重载焊接机器人各关节传输路线

前三个关节在电机和齿轮中间安装了RV系列的减速器，通过驱动齿轮来传递动力，使重载焊接机器人的主体、大臂和小臂进行回转，其回转的角度就是在运动学求解中的θ1、θ2和θ3。后三个关节安装的电机通过齿轮副驱动传动轴，来提供重载机器人腕部的工作动力[3]。不同关节使用的传动方式、电机型号、减速器型号和齿轮副有一定的差异。由于电机的安装位置要尽可能的安装在靠近基座的垂直线上，所以B和T关节采用了轴进行动力传递。

1.2 重载焊接机器人各关节刚度求解

利用不同部件刚度求解的经验公式，求出各个部件的刚度值，并且根据具体的公式折算出各关节的刚度，本文所求的是重载焊接机器人本体的刚度，没有考虑伺服电机的刚度，把它看作为刚性元件。

1.2.1 前三个关节刚度计算

1)关节S刚度求解

重载焊接机器人关节S主要有电机和RV减速器组成，电机的型号是SGMGH-44A2A，RV减速器型号是320C。查的RV-320C型号减速器的扭转刚度为K′R1=17359In-1b/arc.min，由单位换算公式1In-1b/arc.min=388.08Nm/rad可得在关节S中RV减速器的扭转刚度为：

KR1=17359×388.08=6.74×106(Nm/rad)

(1.1)

由此求得关节S的等效静刚度为：

(1.2)

按照上面的方法计算出关节L和关节U的刚度

2)关节L刚度

(1.3)

3)关节U刚度

(1.4)

1.2.2 后三个关节刚度计算

1)关节R刚度求解

重载焊接机器人关节R主要有电机、绷紧连接套、圆柱齿轮副和RV减速器组成，其中，电机的型号是SGMSH-30A2A，RV减速器型号是450E，绷紧连接套在机械中比较通用的一种零部件，具有ISO质量标准，其作用是连接不同机构的两根轴，它具有寿命长、强度高和不易磨损的特点，所以在对各关节刚度进行求解时，把它当刚性部件处理。查的RV-450E型号减速器的扭转刚度为K′R4=9215In-1b/arc.min，由单位换算公式1In-1b/arc.min=388.08Nm/rad可得在关节R中RV减速器的扭转刚度为：

KR4=9215×388.08=3.58×106(Nm/rad)

(1.5)

减速器的减速比为59，齿轮副的减速比为25/70，其各个齿轮的参数如表2所示：

表2 关节R齿轮副参数表

说明：表格中长度单位为mm，弹性模量单位为Gpa。

根据齿轮的扭转刚度的计算公式：

(1.6)

把小齿轮、大齿轮齿轮的参数带入到公式(1.6)中可计算出齿轮的刚度：

K′i1 =9.86×104Nm/rad，K′i2

=7.80×105Nm/rad

(1.7)

根据齿轮的扭转刚度在关节中的等效刚度换算公式：

(1.8)

所以求得小齿轮和大齿轮的扭转刚度在关节R中的等效刚度分别为：

=2.69×109Nm/rad

(1.9)

Ki2=7.80×105×592=2.71×109Nm/rad

(1.10)

由此求得关节R的等效静刚度为：

(1.11)

按照关机R刚度求解的方法，求出关节B和关节T的刚度：

=6.44×105(Nm/rad)

(1.12)

=2.29×105(Nm/rad)

(1.13)

通过以上步骤的计算求出了重载机器人各个关节的刚度，结果如表3所示：

表3 重载机器人各关节刚度

从结果中可以分析出各个运动关节刚度小的地方，选择不同型号的减速器对刚度有一定的影响，使用传动轴进行传递会降低其刚度，末端关节由于在传动过程中使用了传动轴，所以其刚度也就降低了。因此，在对重载机器人进行设计时，要考虑到减速器和驱动力传输路线。

2 大臂与小臂变形分析

2.1 受力分析

通过上面对机器人连杆静力学平衡的分析，可以结合本论文所研究的165kg机器人的大臂和小臂进行力和力矩的求解。其中大臂主要受两端的反力F2r和F2a、力矩M2r和M2a、自重G2，其受力简图如1所示：

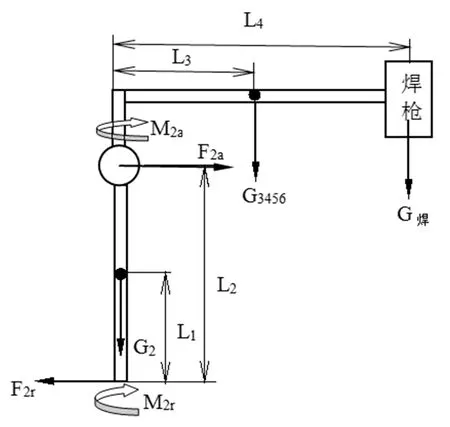
图1 大臂受力简图

根据受力简图可以确定所受的力和力矩的大小，重载焊接机器人大臂所受各个力和力矩计算公式为：

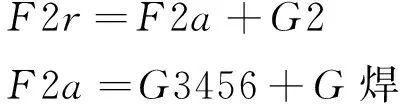
(2.1)

(2.2)

机器人小臂的受力如图2所示：

图2 小臂受力简图

通过上图可知，重载焊接机器人小臂所受的力和力矩计算公式为：

(2.3)

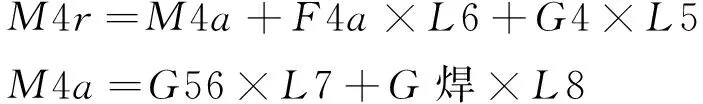
(2.4)

通过对大臂和小臂的受力分析，计算的结果如表4所示：

表4 力与力矩计算结果

2.2 应力与变形分析

重载机器人大臂和小臂是通过铸造而成的，所使用材料的具体属性如下表：

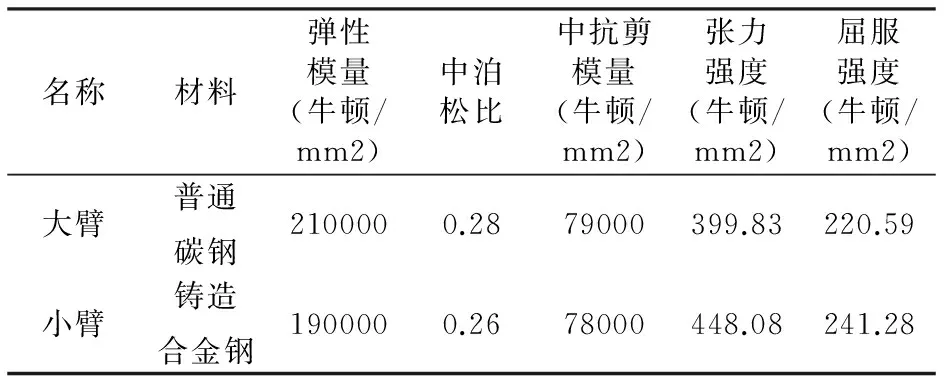
表5 材料属性

对大臂和小臂用Simulation进行应力与静态变形分析，根据上面所求出的力以及重心坐标设置其受力的大小及作用点，静应力分析的网格如下图所示：

图3 大臂网格划分

图4 小臂网格划分

分析的结果主要为应力、应变和位移，其位移量表示其变形量，利用Simulation所分析的是静应力，即在物体静态下进行分析，对应上面所求得的刚度，从而反映出刚度与变形的关系，分析结果如图5—10所示：

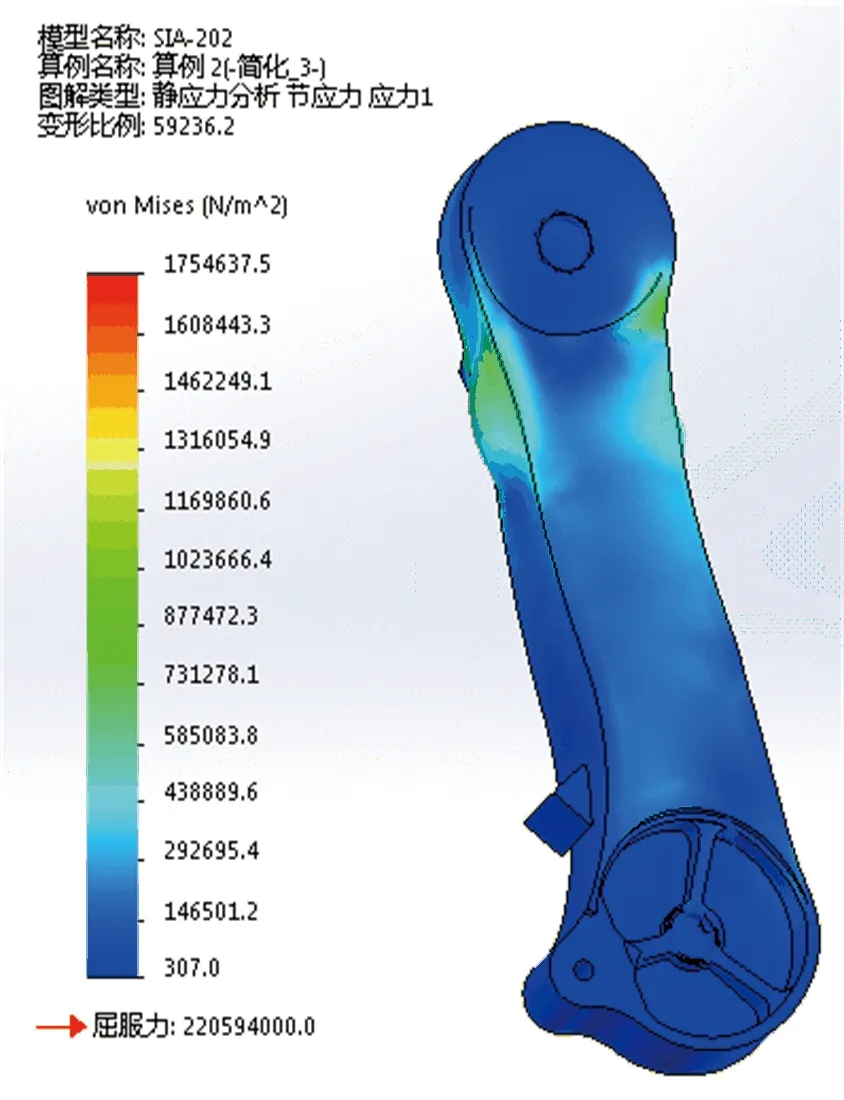
图5 大臂应力

图6 大臂应变

图7 大臂位移

图8 小臂应力

图9 小臂应变

图10 小臂位移

有上面的分析结果可知，大臂和小臂的强度均远小于所用材料的屈服极限，大臂在受静载荷下所发生位移变形量较小，小臂中间部分的位移变形量较大，但是仍在材料变形范围之内，所以设计的大臂和小臂足以满足重载机器人实际的工作需求，具有较高的安全系数。该刚度下机器人的变形量在允许范围之内，经过测得机器人的精度为0.0198mm。

3 结论

机器人的精度跟刚度有一定的关系，如在理想状态下，机器人的各部件均为刚性物体，此时电机的旋转与停止精度决定着机器人的精度。从上面的计算与分析中得出：

1)机器人传动系统中，减速器的刚度要低于其它传动机构，所以减速器的刚度很大程度上决定着机器人传动机构的刚度[4]。由于连接的各个标准件和驱动电机的刚度按照刚性元件进行处理，所以与实际的刚度还存在一定的误差。

2)末端作用力、力矩造成的变形是力作用下线位移、角位移的叠加，分析机器人末端静应力时可单独考虑力与力矩，从而简化分析过程[5-6]。

[1] 李永刚,宋轶民,冯志友．并联机器人机构静刚度研究现状与展望[J]．机械设计，2010(3)：1-4．

[2] 林义忠,廖小平,曾剑.6R喷涂机器人操作臂末端刚度的分析[J].广西大学学报(自然科学版),2011(2).

[3] Li Cheng;Xiao Guang Zhang;Yong Sheng Zhao. Redundant Actuation Investigation of a 5-DOF Parallel Robot[J].Applied Mechanics and Materials,2014, 526

[4] 张永贵,刘晨荣,刘鹏.6R工业机器人刚度分析[J].机械设计与制造,2015(2).

[5] Claude Vibet．Symbolic modeling of robot kinematic and dynamics[J].Robotics and Autonomous Systems. 2012, 14: 301-314.

[6] Patrick O. Stalph, Martin V. Butz. Learning local linear Jacobians for flexible and adaptive robot arm control[J]. Genetic Programming and Evolvable Machines, 2012, 13(2).

责任编辑：刘海涛

TP242.2

A

1673-1794(2016)05-0078-04

张小光，芜湖安普机器人产业技术研究院有限公司机械工程师，硕士；邓启超，许德章，安徽工程大学机械工程学院(安徽 芜湖 241000)。

安徽省科技攻关项目(1604a0902125)

2016-02-14