城市轨道交通电气系统网络负荷建模方法研究

王海滨

(中国中铁西南科学研究院有限公司,611731,成都∥工程师)



城市轨道交通电气系统网络负荷建模方法研究

*王海滨

(中国中铁西南科学研究院有限公司,611731,成都∥工程师)

城市轨道交通电气系统网络存在分散性、时变性、随机性、多样性和非连续性等多种特性。介绍了几种常用的经典负荷模型结构。针对该电气系统网络系统的特点,采用带有反馈模拟云数据生成器,应用隶属度函数与经典负荷模型相结合理论,提出一种基于窗函数的负荷模型建模方法,并对该方法进行了仿真验证。

城市轨道交通;电气系统网络建模;窗函数;负荷模型;仿真

Author′s address China Southwest Research Institute of China Railway Engineering Company Limited,611731,Chendu,China

随着城市轨道交通的发展,城市轨道交通的电气网络系统越来越接近安全极限值运行,因此，在选用电气设备、日常监测活动与故障定位等方面就越来越需要精确计算,从而也就需要精度更高的城市轨道交通电气网络系统建模。

电气系统仿真计算与实际情况的吻合程度取决于所采用的模型的准确性。正确考虑负荷模型的作用,不仅可以改变计算的精度,而且在某些临界状态,还可能改变定性的结论[1]。

电气网络负荷波动中存在大量的随机和模糊现象,由于受目前系统采用的辨识方法和辨识模型所限,无法准确逼近真实的负荷特性[2]。负荷建模方法一般分为统计综合法和总体测辨法。统计综合法以各种典型负荷的平均特性方程为基础综合得出该负荷点的负荷模型[3-5],计算复杂;而总体测辨法建立符合实际的动态负荷模型需要有大量的基础数据作为研究的基础。

本文将带有反馈的组合云发生器作为数据发生器,生成试验数据,并采用总体测辨法进行建模。针对负荷建模的特点,应用基于窗函数与经典负荷模型相结合的建模方法,得到的模型精度高,适用于在线和离线系统。

1 负荷模型结构

1.1 静态负荷模型

1.1.1 多项式模型

常见的多项式模型为经典的“ZIP”模型[6]；

(1)

式中:

P——有功功率;

Q——无功功率;

P0——初始运行工况有功功率;

Q0——初始运行工况无功功率;

U——电压;

U0——初始运行工况电压。

aP,bP,cP,aQ,bQ,cQ——相关多项式系数,表示各部分占有的比重,且有aP+bP+cP=1,aQ+bQ+cQ=1 。

通常用这种模型来表示被研究系统初始运行工况下的某一母线负荷值。电压二次项相当于恒定阻抗负荷,电压一次项相当于恒定电流部分,电压零次项相当于恒定功率部分。

1.1.2 指数模型

用幂系数作为负荷静态特征系数,可反映负荷静态特性。指数模型的一般形式为:

(2)

式中:

f——母线电压频率;

f0——母线电压额定频率;

np——负荷的有功功率/电压特征盾数；

fp——负荷的有功功率/频率特征盾数；

nQ——负荷的有功无协/电压特征盾;

fQ——负荷的有功无协/频率特征盾数。

常用幂虽数模型在电压变化范围交大时，仍能较好地描述负荷的静态特征，因此广泛用于负荷建模。

EPRI 负荷建模计划所支持开发的软件包LOADSYN 中采用了以下模型:

(3)

式中:

P0——母线的初始运行工况有功功率;

Q0——母线的初始运行工况无功功率;

V0——母线初始运行工况电压;

f0——母线的初始运行工况频率;

Δf——母线频率差,Δf=f-f0;

Pa1——与频率有关的有功功率;

Qa1——与频率有关的无功功率;

KPU1——负荷有功电压静态系数1,与频率有关;

KQU1——负荷无功电压静态系数1,与频率有关;

KPU2——负荷有功电压静态系数2,与频率无关;

KQU2——负荷无功电压静态系数2,与频率无关;

KPf1——负荷有功频率静态系数1;

KQf1——负荷无功频率静态系数1;

KQf2——负荷有功频率静态系数2。

上述两种形式多项式模型和指数模型,其本质是一致的,其参数也可以相互转换。应用传统的最小二乘法,极大似然法等系统辨识方法都可以得到结果。此类模型只适合于静态模型建模。

1.2 输入输出动态负荷模型

1.2.1 常微分方程模型

一般形式为:

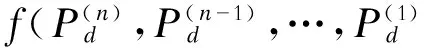
Pd,U(m),U(m-1),…,U(1),U=0

(4)

式中:

U(i)——U的高阶微分。

从分析负荷对阶跃电压响应的特征出发,结合电压稳定研究的需要,可表示为以下形式的模型:

(5)

Ps(U)=CsUαp

(6)

式中:

TP——线性时间常数;

Ps(U)——静态负荷项,一般采用指数表达形式;

kp(U)——动态负荷项,一般采用电压的一次或二次多项式的形式。

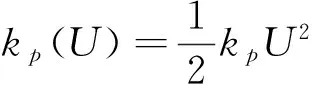
(7)

1.2.2 传递函数模型[6]

一般形式为:

(8)

式中：

a,b——多项式系数；

s——变量。

台湾电力公司通过现场试验,认为三阶模型对于台湾电力系统是适用的。

1.2.3 状态空间模型

状态空间模型一般形式为:

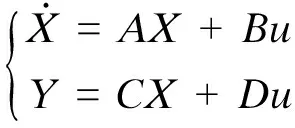
(9)

式中:

A,B,C,D——模型系数;

X,u——输入变量;

Y——输出变量。

1.2.4 时域离散模型

时域离散模型的一般形式为

式中:

a,b,c——相关系数;

P——功率;

U——电压;

f——频。

各变量下标表示该变量在时域坐标的发生序号。

1.2.5T-S模糊模型

T-S模糊模型的描述为,假如给定一个广义输入向量(x10,x20,…xm0),那么由各个规则的输出yi(i=1,2,…,n)的加权平均可求得输出[6]:

(11)

式中:

n——模糊规则的数量;

yi——由第i条规则的结论方程式求取;

Gi——对应此广义输入向量的第i条规则的真值。

Gi由下式确定

(12)

其中, ∏是模糊算子,通常采用取小运算或乘积运算。

T-S模糊模型辨识经过前提结构的辨识、前提参数的辨识、结论参数的辨识及结论结构的辨识、经过对性能指标的计算选出最优模型。理论上划分的前提结构越多,精度就越高;但划分的前提结构越多,最终参数的获得时延也就越大。由于此类模型需要多次辨识进行优化参数筛选,故需要相当长的计算时间。

输入输出式负荷模型相比机理式负荷模型确定参数要容易些,但其缺点就是用数学公式掩盖了物理本质。总体测辨法中常采用此类模型,用模拟进化类算法计算,虽具有全局寻优特性但计算时间过长[7-8]。

2 数据发生器

利用正向云发生器和逆向云发生器组成的组合云发生器设计数据发生器。数据发生器的工作流程如图1所示。其中,云滴数据包括电压值、有功功率值和无功功率值。

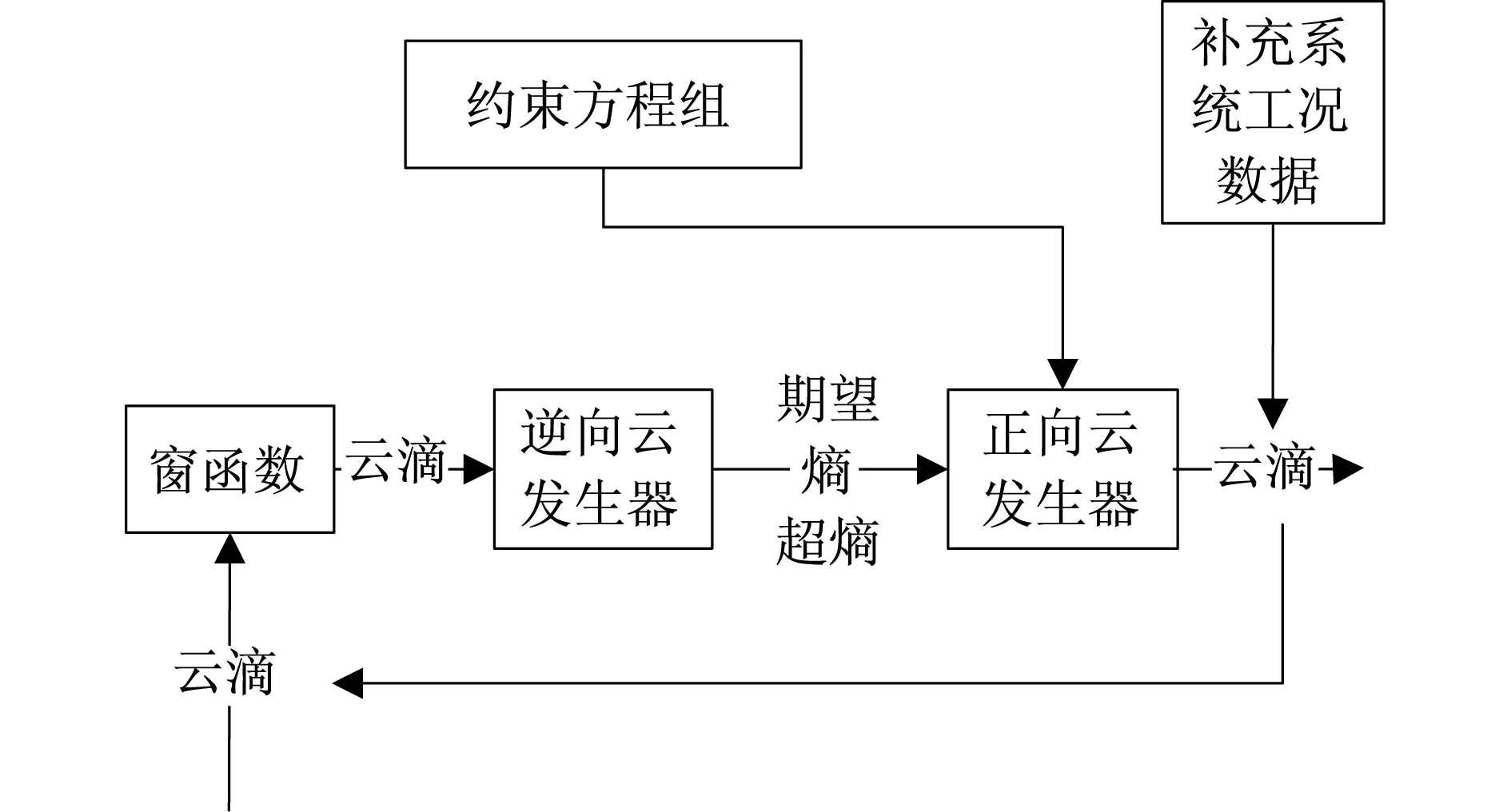
图1 数据发生器

组合云模拟数据发生器用原始数据的数字特征生成试验数据是一种有效的获取基础数据的方法,在一定程度上能解决电气系统故障数据难以获取的难题[9]。

3 窗函数和隶属度函数

窗函数在该算法中的作用是选取合理时间段内的输入云滴。在获取一定数量的输入值后进行建模。为了对负荷曲线进行拟合,首先需进行数据截断选取建模有效数据,即加窗函数处理。

常用的窗函数有矩形窗、三角窗Hamming窗和Blackman窗等形式[10]。

根据实际应用,选取的建模数据应当具有实时性,并对计算输出结果影响权值最大。因此,选取矩形窗函数按时间对输入云滴进行截取,即可满足算法要求。截取时，在窗内的电压和功率值为有效输入数值,在窗外的值为无效值。矩形窗函数为

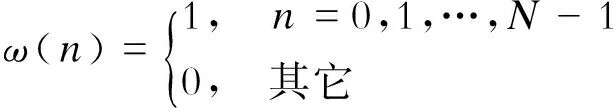
(13)

以对有功功率进行建模为例,假设用功率函数p(t)去拟合一批测量的电器网络数据,对应某个时刻的功率输出值。由于每个输入值t都不同,故窗内每个输入值对计算结果影响权值也不同。为了抑制时间较远的点对最终负荷输出产生的影响,加强时间相近的点对当前时刻点输出值的影响,本文引入隶属度函数进行算法研究。隶属度函数可以是任意形状的曲线,唯一的约束条件是隶属度函数的值域为[0,1]。模糊系统中常用的隶属度函数有高斯型隶属度函数、钟形隶属度函数、sigmoid隶属度函数、三角形隶属度函数和梯形隶属度函数等。

计算某个时刻点的最终输出时,需先对以当前时刻为中轴的矩形窗内输入云滴进行负荷曲线建模。根据实际情况,在当前时刻点的输入云滴值对最终的负荷模型输出影响因子最大,而随着时刻前移和后移,影响因子逐渐变为零。

根据以上分析及分布规律,函数值由中轴逐渐由1变为0的函数符合对窗函数截断航迹点权值特性的描述。由此选取从-1到+1,构造成为一个对称的隶属度函数。根据时间影响计算权值,离计算时刻越近的值,隶属度越大,重合时刻点的隶属度最大,即可满足隶属度函数要求。

值得分析的是,由于建模必须获得一定数量的输入值作为前提,所以对于在线系统来说加入建模算法的在线负荷建模系统必然是存在时延的。窗长的确定是以系统上报数据的时间间隔和系统对时延容忍度、建模精度要求等共同确定的。理论上要求精度越高,则需获得的测量数据也越多,最终参数的获得时延越大。所以,在最终工程实践中,窗长、系统上报数据的时间间隔、系统对时延的容忍度、最终输出结果的精度等共同确定了建模工程中的参数选择和模型形式。

兼顾在线系统与离线系统两种系统的时延和精度要求,本文拟选取的隶属度函数如图2所示。

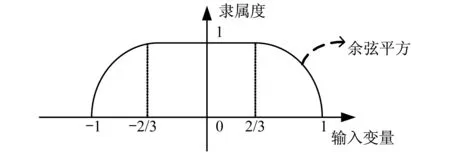
图2 隶属度函数

4 建模与算法研究

假设用功率函数p(t0)去拟合一批测量的电气网络数据,p(t0)是真实数据加误差共同构成的。以正交归一的N次多项式hj(t)为基,展开p(t0),则

(14)

式中:

si——系数。

由于hj(t)是正交归一的,计算可得:

(15)

当t=t0时,

即:

h2(t0)h2(t)+…]p(t)dt

(17)

将上式表示成为

(18)

其中wt0(t)为

h0(t0)h0(t)+h1(t0)h1(tt)+

h2(t0)h2(tt)+…

(19)

一般wt0(-1)≠wt0(1),选取固定窗函数对数据进行加窗处理。设窗长足够小时二次多项式模型在窗函数区间中可以在误差范围内完成建模,此时wt0(t)可选取为最高,且为二次的多项式进行计算。由于h(t)是固定的正交归一的基,所以t0对应的wt0(t)为1个确定的一元二次多项式。设a2、a1、a0分别为二次项、一次项、常数项系数,则可将

表示为

wt0(t)=a2t2+a1t+a0

(21)

对数据加窗处理并归一化到-1到1范围内之后,选择t0为1个常数C,则wt0(t)在整个计算过程中为唯一确定的表达式。如果t0=0,即窗的中间时刻为输出值,则对于在线辨识系统来说,模型输出结果会滞后1/2窗长的时间。表达式的系数随窗函数的不同而不同,随t0的不同而不同。设窗内每一个时刻输入值对应的权函数为fq(t),则t=t0时,拟合结果为

(22)

计算出每一个在窗内的测量点的时刻对应的wt0(t)fq(t)的值,再据实际意义进行离散化,p(t0)可表示为:

(23)

式中:

Mi——输入点的隶属度值。

建模与参数计算流程如图3所示。

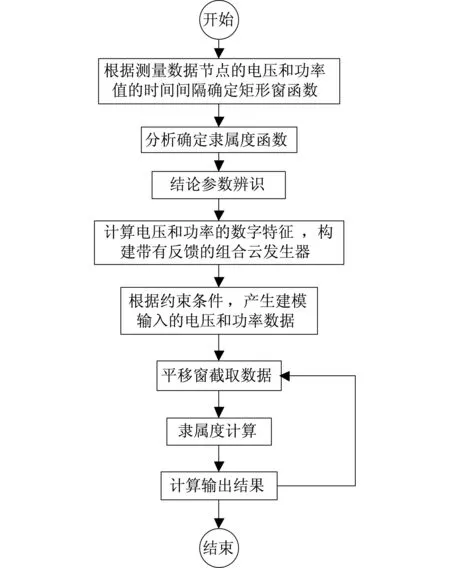
图3 建模与计算流程图

5 仿真结果

以某地铁线路电气系统为例进行仿真研究,系统结构如图4所示。假设不同节点发生两相短路、三相短路、两相对地短路,则通过计算可得到该电气网络线路正常运行情况下节点的170组峰谷负荷波动数据,以及30组短路故障数据。以这200组数据为仿真研究的对象。

以所选择节点A通过数据发生器模型生成的数据为例,兼顾在线系统的时延问题,取t0=2/3,则计算模型的系数见表1。图5为图4中A节点的原始有功功率时序图。仿真图像如图6所示。

对比仿真结果可见,本文所述模型可很好地对输出功率的时序图进行建模。也可采用同样的方式对电压和无功功率进行时序图建模,由此通过模型计算精确得出在某时刻关注点轨道交通电器网络的功率值及电压值等。

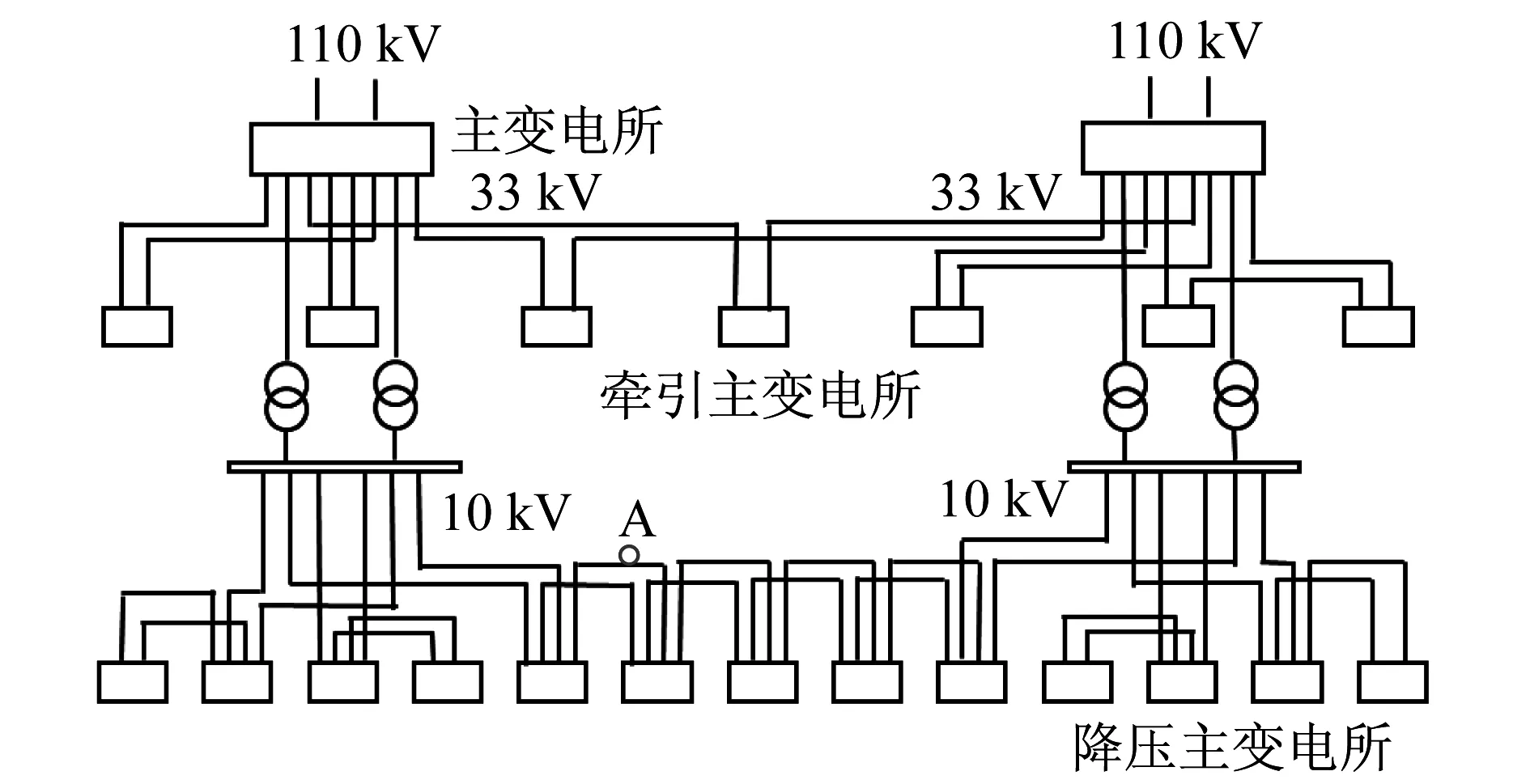
图4 某地铁线路电气系统网络示意图

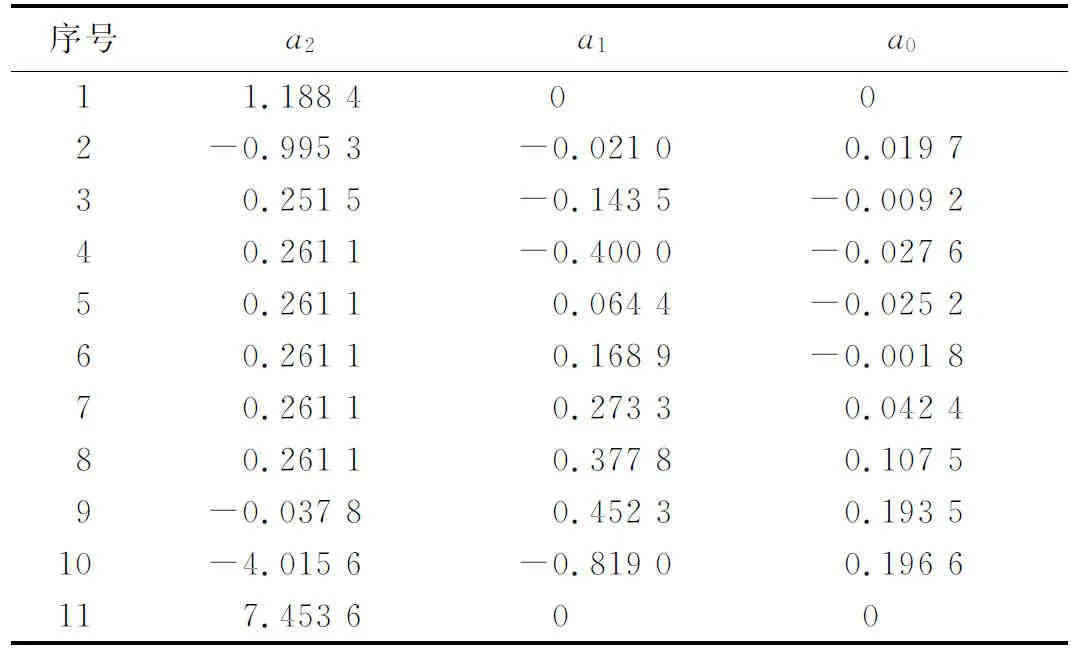
表1 计算模型系数

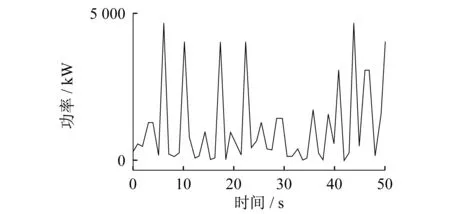
图5 A节点原始有功功率时序图

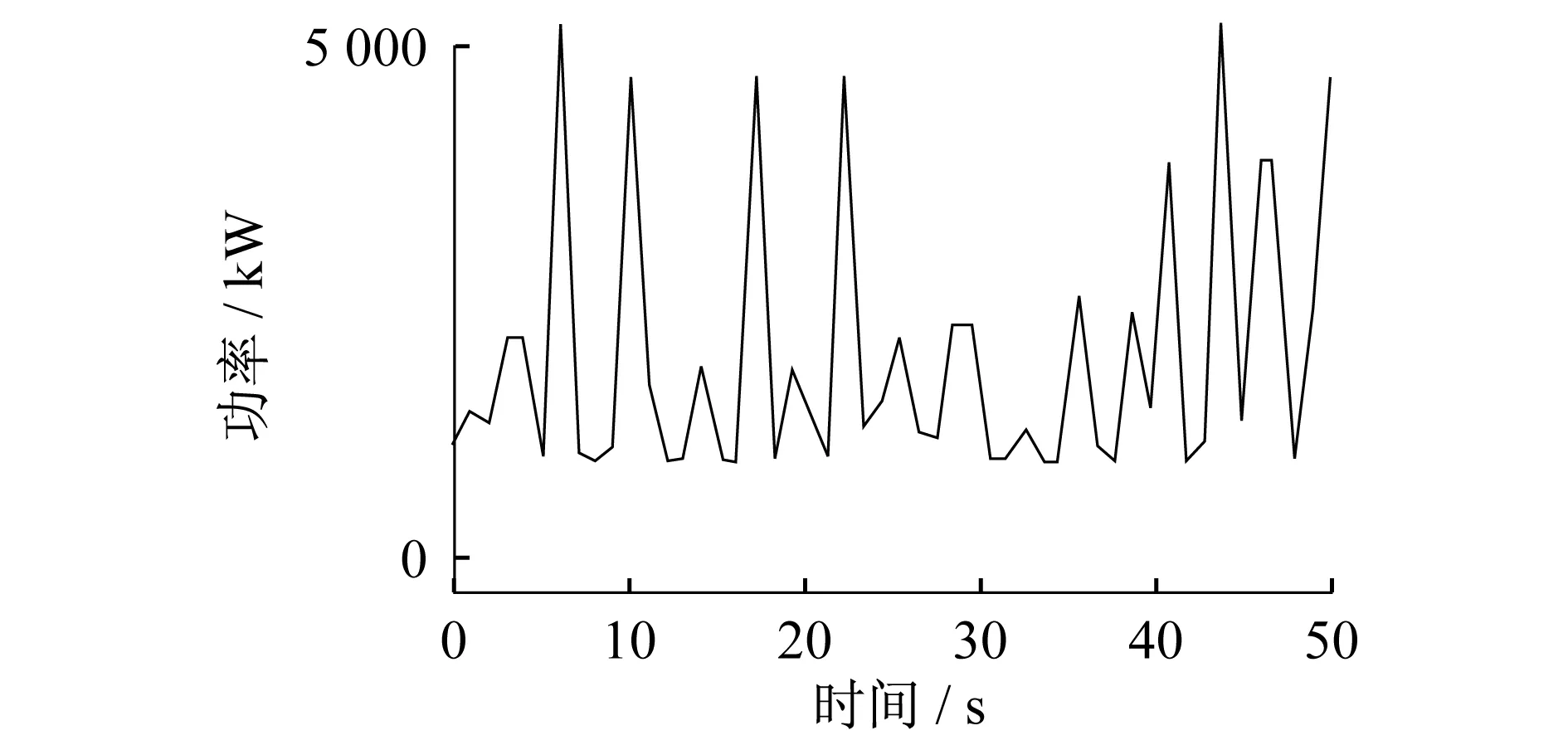
图6 A节点对有功功率建模的结果时序图

6 结语

针对轨道交通电气系统特点,本文采用了带有反馈的模拟数据生成器,应用基于窗函数与经典负荷模型相结合的建模方法,得到了适用于在线系统和离线系统的模型。该模型可在快速计算的基础上基本描述真实情况,其仿真结果证实了该模型的有效性。但加入建模算法的在线负荷建模系统输出结果必然是存在时延的。在工程实践中,窗长、系统上报数据的时间间隔、系统对时延的容忍度及最终输出结果的精度等共同确定了建模工程中的参数选择和模型形式。

[1] 蒋蕾,曲祖义,沈善德.综合测辨法在东北地区电力负荷建模中的应用[J].东北电力技术,1999(7):1.

[2] PRABHA Kundur.Power system stability and control[M].USA:McGraw-Hill,1994.

[3] LOUIE K W,MARTI J R.A method to improve the performance of conventional static load models[J].IEEE Transactions on Power Systems(S0885-8950),2005,20(1):507.

[4] LU Ning,CHASSIN D P,WIDERGREN S E.Modeling uncertainties in aggregated thermostatically controlled loads using a State queuing model[J].IEEE Transactions on Power Systems (S0885-8950),2005,20(2):725.

[5] RUIZ Reyes N,VERA Candeas P,JURADO F.Discrimination between transient voltage stability and voltage sag using damped sinusoids-based transient modeling[J].IEEE Transactions on Power Delivery (S0885-8977),2005,20(4):2644.

[6] 张化光,何希勤.模糊自适应控制理论及其应用[M].北京:北京航空航天大学出版社,2002.

[7] 秦川,顾晓文,王超,等.电力负荷模型参数辨识的混合优化算法[J].河海大学学报(自然科学版),2013,41(6):542.

[8] YANG Jing,WU Min,HE Yong,et al.Identification and application of nonlinear dynamic load models[J].Journal of Control Theory and Applications,2013,11(2):173.

[9] 孙秋野,张化光,王云爽.基于组合云发生器的配电系统负荷模糊建模[J].系统仿真学报,2008,20(2):341.

[10] 王桦,许家栋.旋转目标R-D成像算法中窗函数的选择[J].弹箭与制导学报,2005,25(4):753.

Modelling of Urban Rail Transit Electric Net Load

WANG Haibin

rban rail transit electric network features dispersiveness, time variantion, randomness and discontinity. Aiming at the characteristics of urban rail transit electric network, a simulation data generator with feedback is adopted, and the arithmetic of load model based on window function is proposed by combining the membership degree function with classical load model. A simulation verifies the result of the modelling.

urban rail transit; electric network modeling; window function; load mode; simulation

*国防科技重点实验室基金资助项目(9140C100401120C1001)

TM 743: U 231

10.16037/j.1007-869x.2016.06.012

2014-09-01)