相位检测误差对链式静止同步补偿器稳态输出精度的影响

戴丽君 杨立新

(1.南京铁道职业技术学院铁道供电系,210031,南京;2.铁道第三勘察设计院集团有限公司,300142,天津∥第一作者,副教授)



相位检测误差对链式静止同步补偿器稳态输出精度的影响

戴丽君1杨立新2

(1.南京铁道职业技术学院铁道供电系,210031,南京;2.铁道第三勘察设计院集团有限公司,300142,天津∥第一作者,副教授)

无功补偿技术能有效提高电力牵引供电系统的供电质量。链式静止同步补偿器(STATCOM)需要对电网电压相位进行准确跟踪,以向系统补偿合适的无功,然而相位检测偏差会降低装置输出电流的精度。分析了在解耦控制和分相瞬时电流控制两种控制策略下相位检测误差所带来的影响,并推导出稳态电流精度与相位检测误差及无功电流指令之间的关系式,得到在满足稳态精度时不同无功电流指令下相位检测误差的容许范围;最后通过仿真验证理论分析的正确性。

相位检测误差; 输出精度; 链式静止同步补偿器

First-author′s address Nanjing Institute of Railway Technology,210031,Nanjing,China

城市轨道交通供电系统的感性无功主要由各种电力变压器、电缆、整流机组和动力照明负荷等产生,而容性无功主要由电缆和电容器产生。电气化铁道牵引供电系统因其冲击性、不对称性和非线性供电等原因,也会产生负序、谐波以及无功功率。这些对电网的电能质量影响较大,故需要治理。城市轨道交通和电气化铁道的供电系统常采用无功补偿装置，如静止同步补偿器(STATCOM)。STATCOM也称静止无功发生装置、动态无功补偿装置(SVG),既可补偿感性无功,又可补偿容性无功,同时也能补偿一部分谐波电流,可有效地解决用电负荷对供电系统带来的冲击、非对称性及非线性所带来的电能质量问题,提高系统稳定性。同时，无功电流的控制也是综合自动化系统的重要组成部分。

链式结构(CMC)具有模块化程度高、谐波特性好、单体功率等级低等优点,在STATCOM领域得到广泛应用。链式STATCOM控制中需要对电网电压相位进行准确跟踪,用以产生一个与电网电压同步旋转的矢量,以向系统补偿合适的无功。而相位检测偏差会对链式STATCOM的性能产生一定的影响。

造成相位检测偏差的原因主要有以下3个方面:①采样电压传感器(PT)误差(如PT原副边中心点发生偏移等),其产生的相位检测偏差是一定的;②采样滤波电路的延时,其造成的相位误差大小取决于采样滤波的时间常数;③所采用的锁相环(PLL)精度,PLL的性能评价指标为稳态精度及动态响应速度。

在稳态控制精度方面，相关标准要求稳态时STATCOM装置实际输出与参考指令之间的最大允许偏差为±1%～±2.5%。这个偏差主要和链式STATCOM的控制器性能有关,但实际相位检测误差也会影响其输出偏差。

本文主要分析相位检测误差对链式STATCOM稳态输出精度的影响。

1 链式STATCOM数学模型

图1为采用三角形连接的链式STATCOM电路结构图。其中，Udc1、Udc2、…、UdcN为任一相链节直流电容电压,usa、usb、usc为电网相电压,isab、isbc、isca为——相电流，urab、urbc、urca为三相链节交流端口输出电压;L和R为并网电感及其等效电阻,N为一相链节单元数。

图1 链式STATCOM电路结构图

对于三角形连接的链式STATCOM,其数学模型为

(1)

因为系统的稳定性只与控制器的稳定性相关,而相位检测误差并未改变控制器,所以相位误差不会影响到整个系统的稳定性,只会带来稳态误差。

为分析稳态时相位检测误差所带来的影响,本文作如下限定:①控制器是稳定的,且跟踪性能良好,无静差;②控制目标为输出恒定幅值的无功电流,且稳态误差中不包括有功电流;③控制器检测到的相位与实际电网相位的差值为相位检测误差γ,且稳态时相位检测误差恒定。

2 不同控制策略下相位检测误差的影响分析

2.1 解耦控制下相位检测误差的影响分析

将链式STATCOM数学模型从三相静止abc坐标系变换到两相同步旋转dq坐标系,并使得d轴与电网电压矢量同相,旋转3/2变换矩阵为

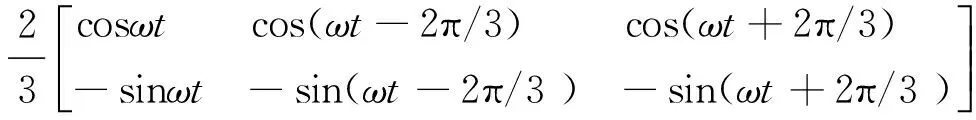
(2)

dq坐标系下的链式STATCOM的数学模型为

(3)

图2为链式STATCOM的解耦控制框图[17,18]。

图2 链式STATCOM解耦控制框图

当控制器检测相位存在误差时,旋转3/2变换矩阵为:

(4)

(5)

式中：

Isd——实际有功电流；

Isq——实际无功电流。

Isd由系统的损耗所决定,工作状态一定时其有功损耗也一定。经变换可得

(6)

2.2 分相瞬时电流控制下相位误差的影响分析

三角形连接的链式STATCOM可等效成3个独立的单相逆变器来控制。有关文献提出了一种分相瞬时电流控制策略,其控制框图如图3所示。以一相系统为例,系统达到稳态时输出电流为

式中：

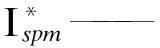
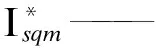
由上式得

(8)

式中：

Ispm——实际有功电流指令的幅值；

Isqm——实际无功电流指令的幅值。

由于式(2)为等幅值变换,所以在相同条件下有

(9)

这样,式(6)与式(8)完全相同。这证明γ对系统输出的影响和控制策略无关。这从物理含义上可理解为,系统达到稳态后,γ所产生的影响是一定的,与达到这个稳态的调节过程无关。

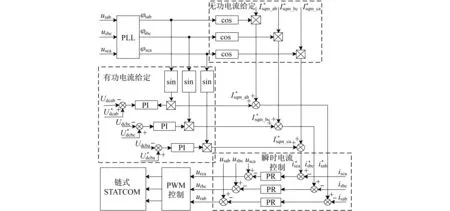
图3 链式STATCOM分相瞬时电流控制框图

3 相位检测误差影响的量化分析

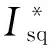
(10)

(11)

式中：

k——实际有功电流和无功电流的比值,k∈(-∞,+∞)。

根据图1所示的参考方向,有功电流Isd恒为正,若k为正值则表示系统发出无功,反之k为负值则表示系统吸收无功。由于Isd基本不变,所以k值的大小就反映输出无功电流的多少。此外,γ为正值则表示检测相位超前实际相位,γ为负值则表示检测相位滞后实际相位。而在实际系统中γ不可能太大,这里将相位误差范围限定在γ∈[-1,1]。

根据式(11)可作出无功电流误差η与γ及k的关系曲线图,如图4所示。由图4曲线可得如下结论:

(1) |k|越大,输出η就越大,即当指令无功电流指令较小时,η更易受γ的影响；

(2) 发出和吸收无功两种状态受相位偏差影响的程度不同;

(3)γ超前和滞后对系统影响的程度不同。

标准要求STATCOM输出无功精度在±1%以内,则可根据式(11)精确求出在不同的无功电流下,装置所能够允许的最大相位检测误差。表1给出了η=±1%且有功电流比例不同时的γ值。

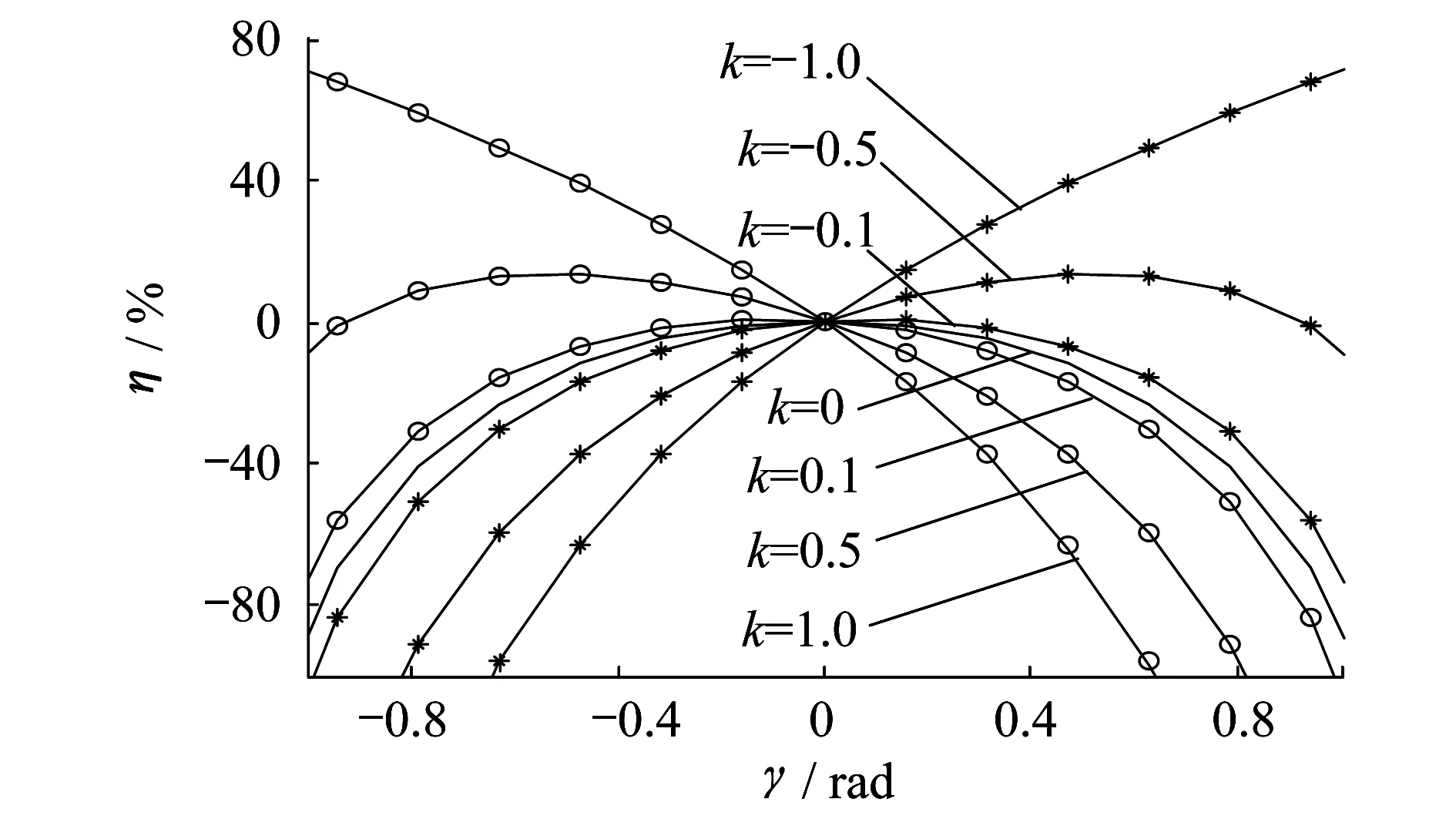
图4 η与γ及k的关系曲线图

表1 η为±1%时不同有功电流比例下的γ

在实际控制器中,γ除了用角度表示还通常以相位延时td的形式来表示。若电网基波周期为Ts,则可用式(12)将γ转换为td:

(12)

对于50 Hz的电网,其Ts=20 ms。根据式(12)可将表1中不同有功电流比例下的相角检测误差角度转换为允许延迟时间范围,结果如表2所示。其中，td为正值表示检测相位超前,td为负值表示检测相位滞后。当k=10时,若锁相延迟超过3.2 μs,则输出误差就会超过1%。不过在实际系统中,有功电流一般很小,k=10时装置已接近空载,即使相位检测偏差造成了输出无功有误差,对电网的影响也很小。

图5为η不超过±1%时,td与k的关系曲线图。图5中曲线所包围范围是满足稳态输出精度要求的区域。

表2 η为±1%时不同有功电流比例下容许的延迟时间范围

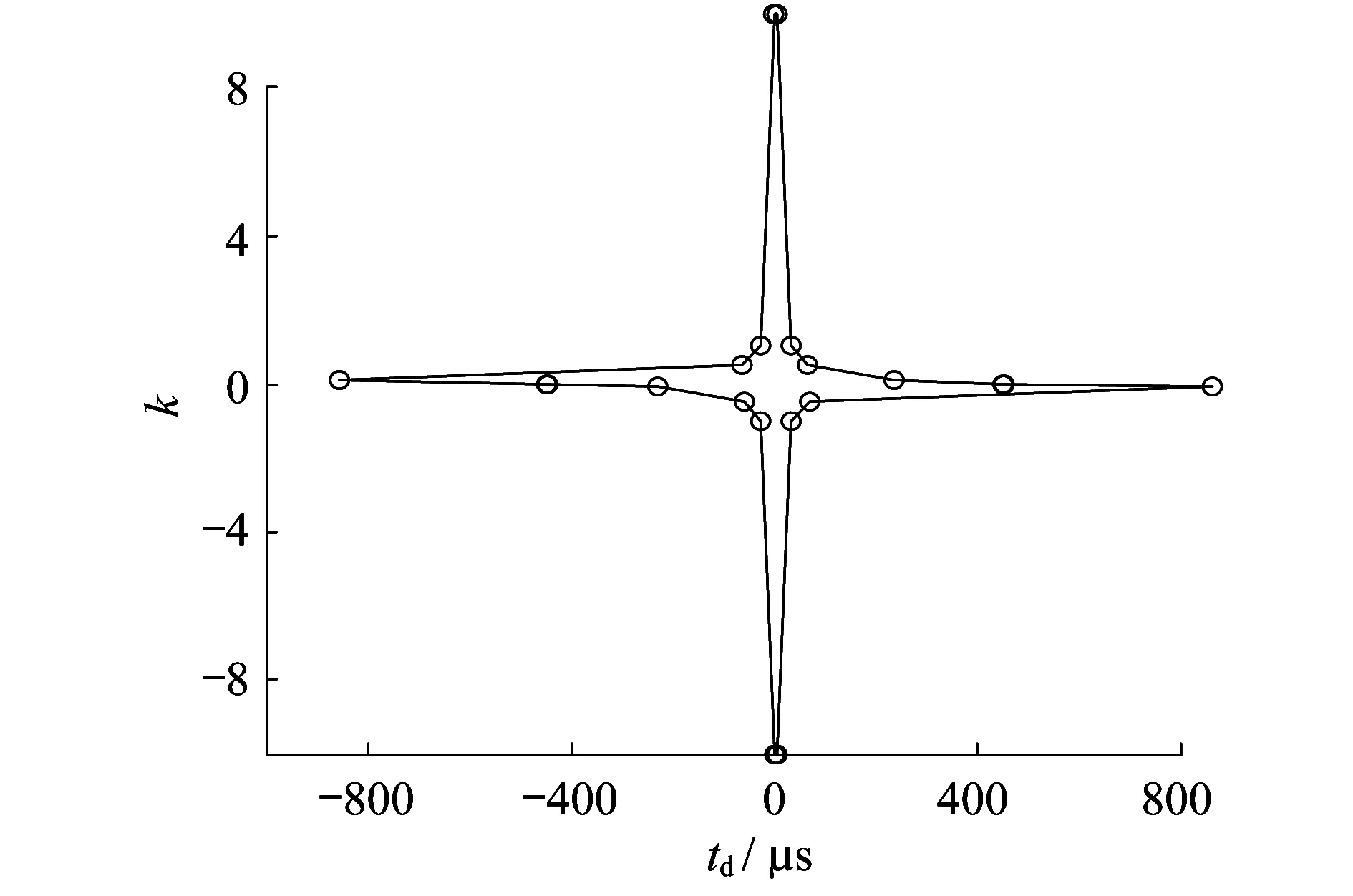
图5 |η|≤1%时td与k的关系曲线图

一般而言,在稳态时γ不大,所以装置输出的η容易达到要求；但在动态过程中,PLL的瞬时偏差可能很大,容易造成过流。若PLL的动态响应时间远小于电流环的响应时间,则PLL的动态过程就可忽略,即使系统电压出现相位突变时也不会存在问题;反之,当PLL速度大于或接近于电流环速度时,装置就存在出现过流的可能。因为在实际中电流环响应时间一般远小于PLL响应时间,电网电压相位严重突变时极容易造成过流,可以考虑采取如下解决措施:

(1) 当系统电压相位发生突变时,装置保护退出或封锁脉冲。这种方法能很好地保证装置的安全,但装置频繁的投入退出不利于装置的安全有效运行。

(2) 减缓电流环的响应时间并加快锁相环响应时间。这种方法是以牺牲装置的动态响应性能来换取装置的安全,并不适合于无功频繁波动的场合。

(3) 当检测到相位突变时,将无功电流指令置为零。该方法可抵御大多数因相位突变而造成过流的风险,其缺点在于不能实时地补偿系统中的无功。

4 仿真验证

为验证上述理论的正确性,在Matlab/Simulink仿真环境下搭建链式STATCOM仿真模型,关键电路参数如表3。

4.1 分相瞬时电流控制仿真验证

图6为系统电压平衡时,链式STATCOM吸收的无功功率由2.5 kVar阶跃至5 kVar的动态响应波形,系统在t1时刻发生无功突变。由仿真波形可知,分相瞬时电流跟踪动态性能良好,无功响应快,另外输出电流与电流指令之间的误差很小(输出电流中的纹波主要是由于开关频率较低以及三次谐波电流造成的)。这表明基于PR控制器的电流环性能良好。

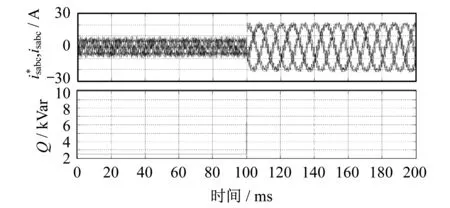
图6 系统电压平衡下无功突变时的动态波形

图7为系统电压不平衡、STATCOM吸收无功功率Q为10 kVar时,A相部分链节的直流电容电压以及输出电流的波形。由图7的波形可知在系统电压出现不平衡时,基于分相瞬时电流控制的链式STATCOM仍能正常工作。

图8为锁相环波形,启动时锁相环延时1/3个工频周期开始准确锁相,在0.06 s时系统电压相位发生突变,PLL迅速跟踪。

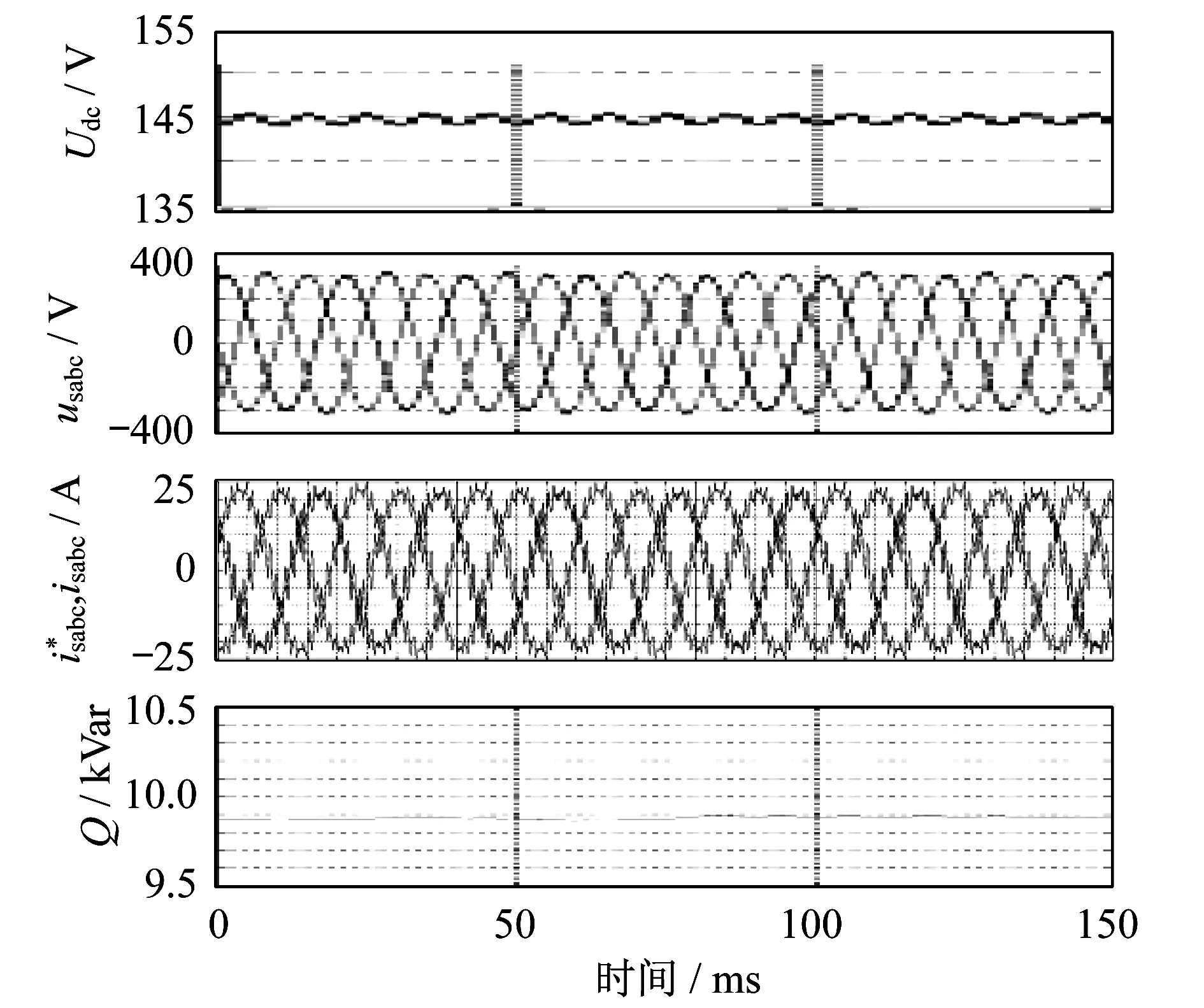
图7 系统电压不平衡下吸收10 kVar无功功率时的稳态波形

图8 系统电压突变时的锁相环输出

4.2 相位检测误差对输出精度影响的验证

图9 γ为0 rad时的并网电流波形

由此可计算出当前功率等级下实际有功电流幅值为Isd=0.868 4 A,而有功电流比例k=0.030 7。

在当前的k下时,根据式(11)可计算出,若要求η=-1%,则γ为0.113 7 rad或-0.270 5 rad。

将仿真模型中STATCOM控制器的相位检测环节设计加入0.113 7 rad的误差,此时ab相链节输出电流波形如图10所示,图中电流isab的峰值为28.571 1 A。认为此时的有功电流不变,仍为Isd=0.868 4 A,而无功电流为Isq=28.557 9 A,则η=0.967%。

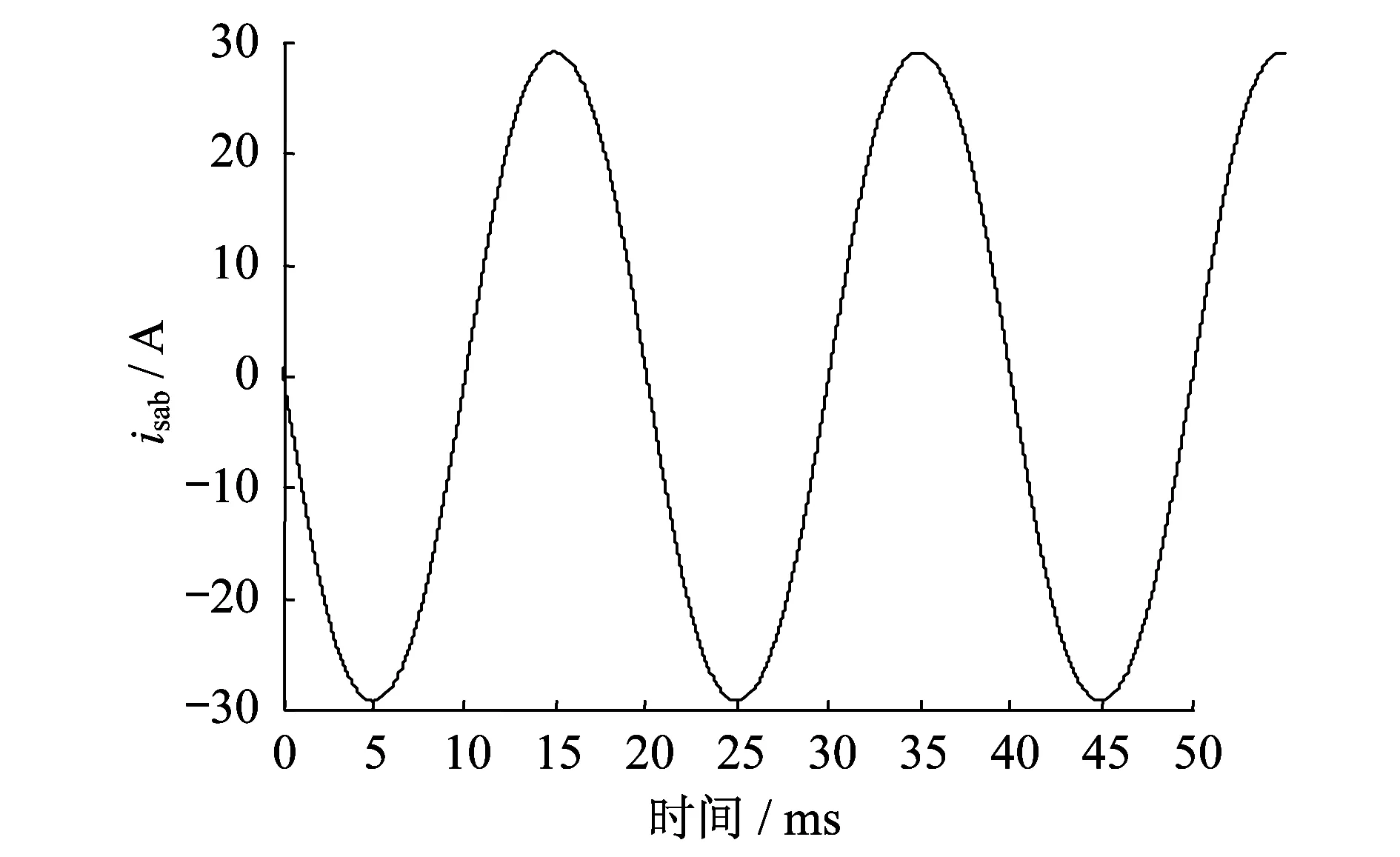
图10 γ为0.113 7 rad时的并网电流波形

将仿真模型中STATCOM的γ改为-0.270 5 rad,并网电流波形如图11所示。其中，isab的峰值为28.570 8 A。同理,有功电流仍为0.868 4 A,则Isq=28.557 9 A，而η=0.966%。

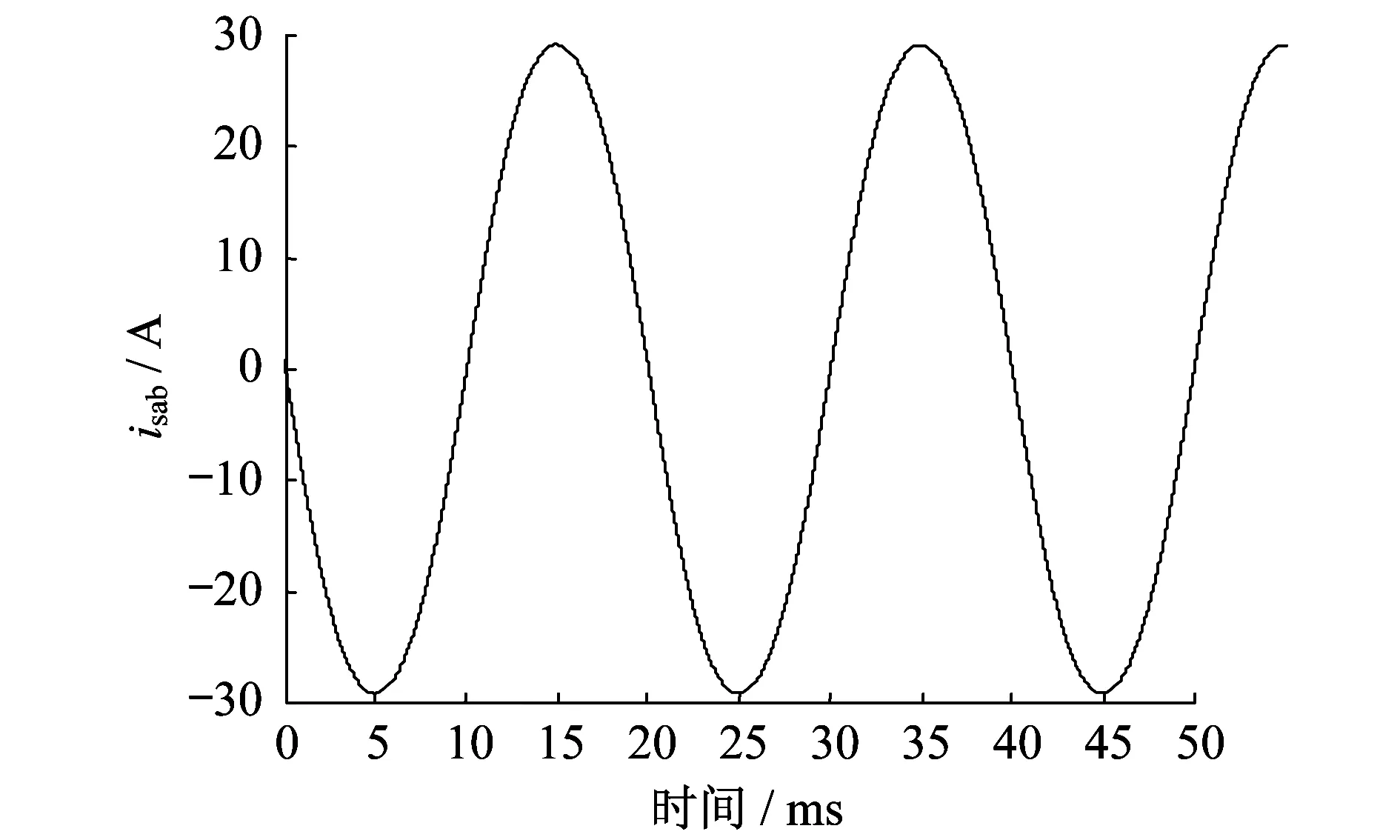
图11 γ为-0.270 5 rad时的并网电流波形

在两种相位检测误差下,仿真得到的无功电流误差均接近1%,验证了计算公式的正确性。只要能够保证γ位于-0.270 5 rad与0.113 7 rad之间,当前运行工况下装置的η就能小于1%。

5 结论

本文详细分析了链式静止同步补偿器中相位检测误差γ对无功输出精度η的影响,指出:①γ对控制系统的稳定性没有影响;②γ只会造成链式STATCOM稳态无功输出存在偏差,而且γ的大小与所采用的控制策略无关;③γ的影响程度与无功指令的大小有关。本文推导了稳态无功输出误差η与γ及无功电流Isq大小之间的关系式,并得到满足输出精度时不同无功电流指令所对应的容许相位检测误差范围,仿真验证了理论分析的正确性。

[1] 周胜军,于坤山,冯满盈,等.电气化铁路供电电能质量测试主要结果分析[J].电网技术,2009,33(13):54.

[2] 荆龙,唐芬,王之赫,等.基于模块化多电平换流器的牵引供电系统电能质量治理方法[J].电力系统自动化,2015,39(11):173.

[3] 严浩军.变电站电压无功综合控制策略的改进[J].电网技术,1997,21(10):47.

[4] IEEE.链式静止同步补偿器 第1部分:功能规范导则:DL/T 1215.1—2013[S].Piscataway:IEEE.

[5] IEEE.南方电网 静止同步补偿器(STATCOM)技术规范:Q/CSG 1101011—2013[S].Piscataway:IEEE.

[6] 刘钊,刘邦银,段善旭,等.链式静止同步补偿器的直流电容电压平衡控制[J].中国电机工程学报,2009(30):7.

On the Effect of Phase Detection Error on Cascaded H-bridge STATCOM Output Accuracy

DAI Lijun, YANG Lixin

Reactive power compensation can effectively improve the power quality of AC traction system. While for the cascaded H-bridge STATCOM, the grid voltage phase must be tracked precisely in order to supply proper reactive power, becuase the phase detection error can decrease the STATCOM output current accuracy. In this paper, influences of the phase detection error under two different control strategies: the decoupling control and the individual phase instantaneous current control are analyzed, the relationship between the steady-state current accuracy, phase detection error and reactive current reference is derived, thus the allowed range of phase detection error under different reactive current references when the steady-state output accuracy could meet the requirement is obtained. The analytic validation is verified by simulation results.

phase detection error; output accuracy; cascade H-bridge STATCOM

U223.5+3

10.16037/j.1007-869x.2016.06.009

2016-01-08)